一種深度偏最小二乘相關分析的多模態(tài)融合方法

蘇樹智 張若楠 郜一瑋 高鵬連 朱剛

摘 要：典型相關分析是一種經(jīng)典的線性多模態(tài)融合方法，但是難以有效解決高維非線性數(shù)據(jù)的多模態(tài)融合問題。結合典型相關分析、線性回歸分析與深度神經(jīng)網(wǎng)絡，提出一種新穎的多模態(tài)融合方法，即深度偏最小二乘相關分析。該方法能夠在最大化不同模態(tài)之間相關性的前提下學習具有強鑒別力的跨模態(tài)融合數(shù)據(jù)，并且能夠有效解決典型相關分析面臨的高維非線性困境。在真實圖像數(shù)據(jù)集上的實驗結果表明，提出的方法具有良好的融合鑒別力和相關收斂性，是一種有效的多模態(tài)融合方法。

關鍵詞：多模態(tài)融合;典型相關分析;偏最小二乘相關;深度學習;圖像識別

中圖分類號： TP391文獻標志碼：A

文章編號：1672-1098（2021）02-0023-06

收稿日期：2020-07-23

基金項目：國家自然科學基金資助項目（61806006）;中國博士后科學基金資助項目（2019M660149）;安徽省“115”產(chǎn)業(yè)創(chuàng)新團隊基金資助項目;合肥綜合性國家科學中心能源研究院基金資助項目（19KZS203）

作者簡介：蘇樹智（1987-），男，山東泰安人，副教授，博士，研究方向：模式識別、深度學習、多模態(tài)數(shù)據(jù)處理。

A Multi-modal Fusion Method via Deep Partial Least Square Correlation Analysis

SU Shuzhi1，2，ZHANG Ruonan1，2，GAO Yiwei1，2，GAO Penglian1，ZHU Gang1

（1.School of Computer Science and Engineering， Anhui University of Science and Technology， HuainanAnhui232001， China;2.Institute of Energy， Hefei Comprehensive National Science Center， HefeiAnhui230031， China）

Abstract：Canonical correlation analysis （CCA） is a classic linear multi-modal fusion method but difficult for CCA to deal with multi-modal fusion of nonlinear data. Therefore a novel multi-modal fusion method， i.e. the deep partial least squares correlation （DPLSC） is proposed by means of CCA， linear regression analysis， and deep neural network， which may maximize the correlation of different modalities and simultaneously learn the cross-modal fusion data with a strong discriminative power. Besides， the nonlinear dilemma and the small size sample problem of CCA will be solved with the method. Experimental results on real-world image datasets reveal that the proposed method is an effective multi-modal fusion one with a strong fusion discriminative power and good correlation convergence.

Key words：multi-modal Fusion; Canonical Correlation Analysis; Partial Least Squares Correlation; deep Learning; image Recognition

典型相關分析（Canonical Correlation Analysis， CCA）[1]是處理多模態(tài)數(shù)據(jù)的統(tǒng)計學方法，旨在最大化不同模態(tài)特征之間的相關性，目前已經(jīng)被成功應用于很多領域。文獻[2]將CCA用于多模態(tài)特征學習和數(shù)據(jù)融合，并在圖像識別中獲得了良好的實驗結果。從不同的角度，文獻[3]通過使用隨機化方法降低典型相關分析的時間復雜度，提出了統(tǒng)計CCA方法，實現(xiàn)投影方向的快速學習。文獻[4]結合核方法，將低維數(shù)據(jù)映射到高維度，以解決在低維度無法解決的非線性困境，提出核化典型相關分析（Kernerl Canonical Correlation Analysis，Kernel CCA）方法，實現(xiàn)對低維非線性數(shù)據(jù)的有效融合，文獻[5]提出一種基于點陣量化的非線性相關分析問題的信息理論壓縮表示框架，使得CCA面對非線性問題時仍能具有較好的性能。文獻[6]將典型相關分析從兩模態(tài)擴展到兩個或兩個以上的模態(tài)，提出了多視圖CCA方法，并在大腦數(shù)據(jù)分析中獲得良好的實驗結果。文獻[7]結合深度神經(jīng)網(wǎng)絡，提出深度CCA（Deep CCA）方法，以解決典型相關分析難以掌握原始高維數(shù)據(jù)的內(nèi)在非線性結構信息。但在現(xiàn)實數(shù)據(jù)環(huán)境中往往會遇到樣本維度較高且樣本與樣本之間又具有較高的相關性的問題，此時基于典型相關分析的數(shù)據(jù)融合將受到較多的限制，為了解決該問題，偏最小二乘（Partial Least Square Method， PLS）[8]方法結合主成分分析、典型相關分析以及線性回歸分析，從理論上解決數(shù)據(jù)融合時的高維線性不可分問題，PLS由于其在上述問題的出色性能，目前已經(jīng)成功應用于醫(yī)學成像分析[8]、生物成分分析[9]、光譜圖像處理[10]、植物特征分析[11]等生物醫(yī)學領域。PLS方法可分為偏最小二乘回歸（Partial Least Squares Regression，PLSR）以及偏最小二乘相關（Partial Least Squares Correlation， PLSC），PLSR旨在用一個模態(tài)的數(shù)據(jù)來推測另一個模態(tài)的數(shù)據(jù)，而PLSC主要用于分析不同模態(tài)之間的相關性問題，本文主要是探索基于PLSC的數(shù)據(jù)融合問題。

CCA與PLSC是線性的優(yōu)化方法，對非線性樣本的適用性較差。深度學習是近年來不斷發(fā)展的新興學科，隨著深度學習的不斷發(fā)展，越來越多的學科通過與深度神經(jīng)網(wǎng)絡結合而達到了相較于過去更好的適用性，截止目前，行為預測[12]、自然語言處理[13]、情感分析[14]、語音識別[15]等領域的深度學習應用已經(jīng)被廣泛采用。本文通過結合深度學習與PLSC，提出一種新穎的多模態(tài)圖像識別方法，即深度偏最小二乘相關分析方法（Deep Partial Least Square Correlation， DPLSC）。該方法將偏最小二乘相關分析和深度學習進行有效融合，深度神經(jīng)網(wǎng)絡的層與層之間的非線性激活對非線性樣本進行處理，偏最小二乘相關分析作為多模態(tài)網(wǎng)絡的融合層，進行相關約束和融合，從而有效增強了多模態(tài)非線性特征的鑒別力，實現(xiàn)了多模態(tài)圖像的有效識別。大量實驗顯示DPLSC方法是一種有效的多模態(tài)圖像識別方法。

1 相關工作

1.1 典型相關分析（CCA）

CCA是一種經(jīng)典的多元統(tǒng)計分析方法，目前被廣泛的應用于模式識別，信息融合以及語義分析等方面，它能夠?qū)W習兩個模態(tài)之間的相關一致子空間，有效地發(fā)掘不同模態(tài)之間潛在的線性相關關系。

令X=[x1，x2，x3，…，xN]∈Rdx×N，Y=[y1，y2，y3，…，yN]∈Rdy×N是對應同一目標的兩個模態(tài)數(shù)據(jù)。其中對應于第k對樣本的數(shù)據(jù)為（xk，yk），N代表采集樣本的數(shù)量，dx和dy分別為兩個模態(tài)數(shù)據(jù)的樣本維數(shù)。CCA旨在通過構建不同模態(tài)的相關準則函數(shù)，學習模態(tài)數(shù)據(jù)集X與Y的相關投影方向α∈Rdx×1和β∈Rdy×1。為了使求得的低維相關投影具有最大的相關性，借助皮爾森相關系數(shù)來構建相關投影準則，具體優(yōu)化函數(shù)如式（1）所示。

maxα，βαTSXYβαTSXXαβTSYYβ（1）

其中SXY=1n∑ni=1（xi-x-）（yi-y-）T為模態(tài)數(shù)據(jù)集X與Y之間的類間協(xié)方差矩陣，另外，SXX=1n∑ni=1（xi-x-）（xi-x-）T和SYY=1n∑ni=1（yi-y-）（yi-y-）T是同一模態(tài)數(shù)據(jù)的類內(nèi)協(xié)方差矩陣，用來反映類內(nèi)的相關程度。由于公式（1）中相關投影方向α和β具有尺度不變性，因此上述相關投影準則能夠等價的轉(zhuǎn)化為下面的相關優(yōu)化問題

maxα，β αTSXY βs.t.αTSXXα=1，βTSYY β=1 （2）

利用拉格朗日乘子法求解能夠?qū)⑸鲜鱿嚓P優(yōu)化問題的求解轉(zhuǎn)化為求解矩陣H=S-1XXSXYS-1YYSYX的前k個最大特征值對應的特征向量。

1.2 偏最小二乘相關（PLSC）

PLSC與典型相關分析相同，都是對于同一觀測物體的不同模態(tài)數(shù)據(jù)進行關聯(lián)處理的方法。PLSC通過推導模態(tài)數(shù)據(jù)的潛在變量空間來得到其最佳的線性組合。

和典型相關分析相比，偏最小二乘相關分析在面對高維度樣本時能夠?qū)W習更具鑒別力的特征，假設X=[x1，x2，x3，…，xN]∈Rdx×N，Y=[y1，y2，y3，…，yN]∈Rdy×N分別為相同目標在不同采集方式下采集到的不同模態(tài)數(shù)據(jù)，其中N代表不同模態(tài)下采集到的樣本數(shù)，dx和dy分別為兩個模態(tài)數(shù)據(jù)的樣本維度，分別對不同模態(tài)下的數(shù)據(jù)進行標準化處理，得到標準化后的數(shù)據(jù)X，Y。通常，由于X，Y進行了標準化處理將X，Y的積R=X YT用于表示X，Y相關性矩陣，對R進行奇異值分解，可以得到R=UDVT，其中U，V均為由奇異值構成的矩陣，在偏最小二乘相關中，U，V代表著模態(tài)數(shù)據(jù)的主要特征。

通過上述的方式得到原始樣本的顯著特征后，需要對樣本的相關性進行分析，通過將原樣本向U，V的方向進行投影即Lx=XV和Ly=YV，PLSC的優(yōu)化目標如式（3）所示。

maxu，v cov（Lx，Ly）

s.t.uuT=1，vvT=1 （3）

其中u，v分別為U，V的前n個向量。將上述優(yōu)化目標以典型相關分析的形式進行具體的表示，即將偏最小二乘分析問題轉(zhuǎn)化為下述優(yōu)化問題

maxu，v uTRvs.t.uuT=1，vvT=1（4）

類似于CCA，利用拉格朗日乘子法同樣能夠獲得上述優(yōu)化問題的解析解。

1.3 深度神經(jīng)網(wǎng)絡（DNN）

深度神經(jīng)網(wǎng)絡（Deep Neural Networks，DNN）是一種模擬大腦神經(jīng)網(wǎng)絡推理模式的機器學習方法。深度神經(jīng)網(wǎng)絡的最小單元是感知機，感知機是一種有多個輸入以及單個輸出的模型，在圖1中給出了感知機模型的直觀描述。

感知機的輸入與輸出之間存在一種線性關系即

z=∑mi=1wixi+b（5）

其中wi為每個輸入的權值，即每個輸入對輸出的影響程度，b則為偏差值。從z到最終的輸出之間往往會添加一層激活函數(shù)，當激活函數(shù)為

sign（z）=1 z≥0-1 z<0 （6）

感知機能夠應用于二元分類問題，顯然，單獨的感知機無法解決復雜的非線性問題，深度神經(jīng)網(wǎng)絡則通過將感知機進行堆疊構建網(wǎng)絡，如圖2所示。

如圖2所示，深度神經(jīng)網(wǎng)絡通過堆疊感知機組成了復雜的網(wǎng)絡結構，這樣的結構可以處理多輸入與多輸出的高維度非線性問題。

2 深度偏最小二乘相關（DPLSC）

本文提出的DPLSC方法，通過將兩模態(tài)數(shù)據(jù)分別通過兩個多層堆疊的神經(jīng)網(wǎng)絡，來對復雜的非線性數(shù)據(jù)進行預處理后，在通過深度偏最小二乘相關方法來計算雙視圖數(shù)據(jù)的相關性，具體的框架如圖3所示。

為了描述的便捷，假設上述框架使用第一個模態(tài)對應的神經(jīng)網(wǎng)絡輸入層有c1個節(jié)點，最終的輸出有個節(jié)點。對于第一個視圖數(shù)據(jù)x1∈Rn1來說，對應神經(jīng)網(wǎng)絡的第一層輸出為h1=s（W11x1+b11）∈Rc1，其中W11∈Rc1×n1為神經(jīng)網(wǎng)絡的第一層權重組成的矩陣，b11∈Rc1為神經(jīng)網(wǎng)絡第一層的偏差值所組成的向量，s（°）為神經(jīng)網(wǎng)絡的層與層之間的非線性激活函數(shù)。

對于第一個視圖數(shù)據(jù)x1∈Rn1來說，對應神經(jīng)網(wǎng)絡的第一層輸出為h1=s（W11x1+b11）∈Rc1，其中W11∈Rc1×n1為神經(jīng)網(wǎng)絡的第一層權重組成的矩陣，b11∈Rc1為神經(jīng)網(wǎng)絡第一層的偏差值所組成的向量，s（°）為神經(jīng)網(wǎng)絡的層與層之間的非線性激活函數(shù)。神經(jīng)網(wǎng)絡第一層的輸出h1，將用于第二層的輸入，按照上述的計算方式，第二層的輸出可以表示為h2=s（W12h1+b12）∈Rc1，通過將上一層的輸出作為下一層的輸入，計算到輸出層（第d層）的最終表示為f1（x1）=s（W1dhd-1+b1d）∈R。對于第二個視圖x2，采用第一個視圖相同的方法，使用不同的權重矩陣W2l與偏差值向5量b2l得到第二個視圖的最終表示為f2（x2）。

深度偏最小二乘相關分析使用兩組深度神經(jīng)網(wǎng)絡同時學習雙模態(tài)數(shù)據(jù)的融合特征，通過不斷更新權重Wvl與偏差bvl使雙視圖數(shù)據(jù)的相關性達到最大。假設θ1和θ2分別為雙視圖數(shù)據(jù)對應神經(jīng)網(wǎng)絡的參數(shù)矩陣，則深度偏最小二乘相關分析的優(yōu)化目標可描述為如下優(yōu)化函數(shù)

（θ*1，θ*2）=max（θ1，θ2）corr（f1（X1;θ1），f2（X2;θ2））（7）

為了求解（θ*1，θ*2），采用梯度下降方法訓練數(shù)據(jù)。令H1∈R×m，H2∈R×m是由大小為m維的樣本數(shù)據(jù)通過深度神經(jīng)網(wǎng)絡得到的相應視圖的最終輸出。H1=H1-1m-1H1L為H1經(jīng)過中心化處理后得到的零均值矩陣，L∈Rm×m為元素全為1的矩陣，對H2進行同樣的中心化處理得到對應的零均值矩陣H2，因此跨模態(tài)相關矩陣R12能夠表示為R12=1m-1H1HT2。

類似于PLSC的求解方法，利用奇異值分解法能夠求解跨模態(tài)相關矩陣R12對應的模態(tài)顯著特征，從參考文獻[17]可知，跨模態(tài)樣本間的相關性能夠通過R12的前n個奇異值之和來表示，當n=時，跨模態(tài)樣本間的相關性corr（H1，H2）為其的跡范數(shù)，即

corr（H1，H2）=R12tr=tr（R12TR12）12 （8）

DPLSC中神經(jīng)網(wǎng)絡的權重參數(shù)Wvl以及偏差值參數(shù)bvl通過梯度下降的方法進行優(yōu)化。為了計算corr（H1，H2）中相應參數(shù)Wvl與bvl的梯度，可以先計算出H1，H2的梯度后在使用反向傳播計算其他參數(shù)對應的梯度。假設R12的奇異值分解為R12=UDVT，則相應的梯度公式為

corr（H1，H2）H1=1m-1（2SymbolQC@11H1+SymbolQC@12H2）（9）

其中SymbolQC@12=UVT，SymbolQC@11=-12UDUT。對于矩陣H2，corr（H1，H2）H2的表達式與上式相同。在表1中描述了詳細的算法步驟。

輸出：具有最大相關性的非線性融合數(shù)據(jù)

在第四部分中，將通過在MNIST手寫數(shù)字數(shù)據(jù)集上的針對性實驗驗證DPLSC相較于其他融合方法能夠得到更好的融合特征。

3 實驗部分

在本節(jié)中，通過在MNIST手寫數(shù)字數(shù)據(jù)集上進行手寫數(shù)字識別，并通過與CCA，PLSC，Kernel CCA，圖多視角典型相關分析（Graph Multiview CCA， GMCCA） [18]，Deep CCA以及本文提出的DPLSC方法的性能進行對比分析。

3.1 MNIST手寫數(shù)字圖像數(shù)據(jù)集

MNIST手寫數(shù)字圖像數(shù)據(jù)集共計由70 000張28×28像素的手寫數(shù)字圖像組成，其中60 000張作為訓練圖像，10 000張作為測試圖像，從本質(zhì)上而言，該數(shù)據(jù)集為單模態(tài)圖像數(shù)據(jù)集，本文利用多模態(tài)圖像策略[19]獲得每幅圖像的兩種模態(tài)數(shù)據(jù)。具體而言，首先將像素值縮放到[0，1]，并對從數(shù)據(jù)集中均勻采樣得到的圖像進行[-π/4，π/4]角度的旋轉(zhuǎn)為第一種模態(tài)數(shù)據(jù);然后從與第一種模態(tài)數(shù)據(jù)相同標簽的圖像中隨機選擇一副圖像，將從[0，1]開始均勻采樣的獨立隨機噪聲加到該圖像的每個像素上，再將像素的最終值截斷到[0，1]，從而獲得第二種模態(tài)數(shù)據(jù)。在圖4中展示了經(jīng)過模態(tài)圖像策略處理后的代表性圖像，其中左圖為第一個模態(tài)的圖像，右圖為第二個模態(tài)的圖像。

3.2 實驗結果分析

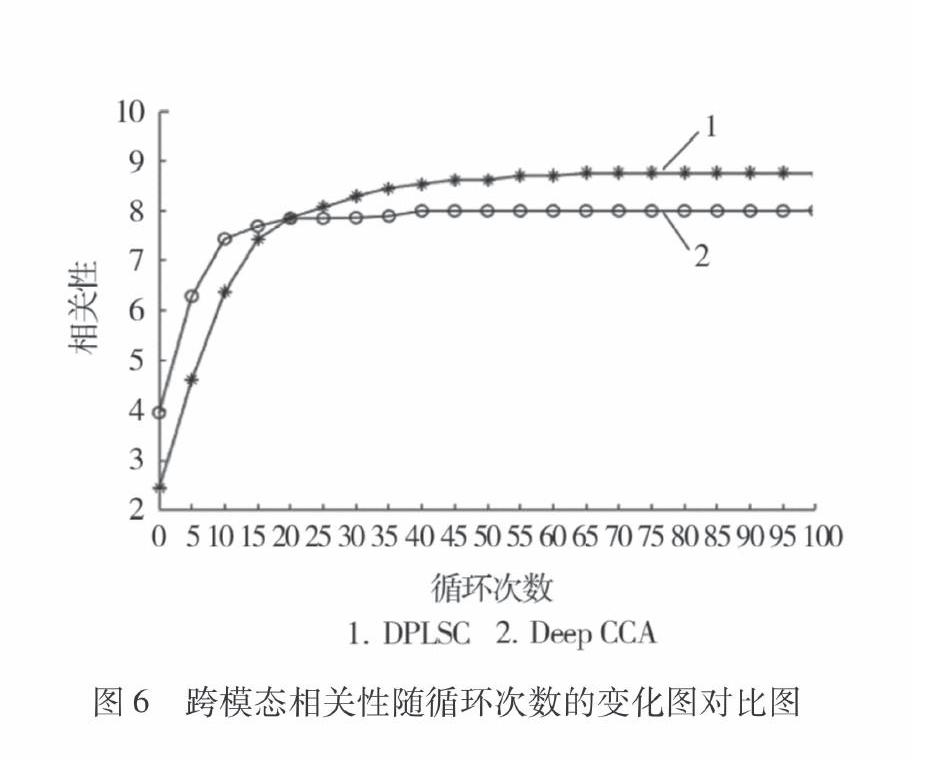
在實驗中分別使用CCA，PLSC，Kernel CCA，GMCCA， Deep CCA以及本文提出的DPLSC對兩模態(tài)圖像數(shù)據(jù)進行低維融合，并將融合數(shù)據(jù)約束在10維、20維、30維、40維以及50維后，利用支持向量機對融合數(shù)據(jù)進行分類，以獲得最終的識別結果。從圖5中可以看出，隨著約束的維度增加，DPLSC的識別率不斷升高，并獲得比其他方法更好的識別性能。當數(shù)據(jù)維數(shù)達到20以上時，本文中提出的DPLSC方法均獲得了最優(yōu)的識別性能，并且識別率隨維度變化同樣更加穩(wěn)定。GMCCA借助圖理論能夠?qū)W習非線性特征，并且隨著維數(shù)的增加，識別率在50維時獲得了比CCA更優(yōu)的識別率。另外，將Deep CCA與DPLSC的最大循環(huán)次數(shù)同樣設定為100次，從圖6能夠看出本文提出的DPLSC方法相較于Deep CCA方法能夠更加充分的學習兩模態(tài)數(shù)據(jù)之間的非線性特征，并取得更大的收斂相關性。上述實驗結果可以給出一個合理的觀察，DPLSC能夠獲得更具鑒別力的融合數(shù)據(jù)，是一種面向識別任務的有效多模態(tài)融合方法。

4 總結

本文提出一種新穎的多模態(tài)融合方法，即DPLSC，該方法能夠在最大化不同模態(tài)之間相關性的前提下獲得具有強鑒別力的跨模態(tài)融合數(shù)據(jù)，該方法利用深度神經(jīng)網(wǎng)絡克服了CCA，PLSC在數(shù)據(jù)融合非線性困境，并有效提升了融合高維數(shù)據(jù)時的融合性能，通過實驗表明，DPLSC獲得的融合數(shù)據(jù)相較于其他融合方法的融合結果更具鑒別力，并與Deep CCA相比具有更好的相關收斂性與對于維度變動的穩(wěn)定性，是一種有效的多模態(tài)融合方法。

參考文獻：

[1] YANG X，WEIFENG L，LIU W，et al.A Survey on Canonical Correlation Analysis[J].IEEE Transactions on Knowledge and Data Engineering，2019，1：1 558-2 191.

[2] SUN Q S，ZENG S G，LIU Y，et al.A new method of feature fusion and its application in image recognition[J].Pattern Recognition， 2005， 38（12）： 2 437-2 448.

[3] GAO C， GARBER D， SREBRO N， et al. Stochastic canonical correlation analysis[J]. Journal of Machine Learning Research， 2019， 20（167）： 1-46.

[4] WANG Y， CANG S， YU H. Mutual information inspired feature selection using kernel canonical correlation analysis[J]. Expert Systems with Applications： X， 2019， 4： 100014.

[5] PAINSKY A， FEDER M， TISHBY N. Nonlinear Canonical Correlation Analysis： A Compressed Representation Approach[J]. Entropy， 2020， 22（2）： 208.

[6] DECHEVEIGNE A， Di LIBERTO G M， Arzounian D， et al. Multiway canonical correlation analysis of brain data[J]. NeuroImage， 2019， 186： 728-740.

[7] ANDREW G，ARORA R，BILMES J，et al.Deep canonical correlation analysis[C]. International conference on machine learning.JMLR.org：Atlanta.GA，USA，2013： 1 247-1 255.

[8] HAIR J F， SARSTEDT M， RINGLE C M. Rethinking some of the rethinking of partial least squares[J]. European Journal of Marketing， 2019， 53（4）：566-584.

[9] ZEIGHAMI Y，F(xiàn)ERESHHTEHNEJAD S M，DADAR M，et al.A clinical-anatomical signature of Parkinson's Disease identified with partial least squares and magnetic resonance imaging[J].NeuroImage，2019，190：69-78.

[10] FOSTER A J， KAKANI V G， MOSALI J. Estimation of bioenergy crop yield and N status by hyperspectral canopy reflectance and partial least square regression[J]. Precision Agriculture， 2017， 18（2）： 192-209.

[11] ALOGLU A K， HARRINGTON P B， SAHIN S， et al. Prediction of total antioxidant activity of Prunella L. species by automatic partial least square regression applied to 2-way liquid chromatographic UV spectral images[J]. Talanta， 2016， 161： 503-510.

[12] BODAH E T，WEIR B.New Method Application for Marker-Trait Association Studies in Plants：Partial Least Square Regression Aids Detection of Simultaneous Correlations[J]. Agricultural research & technology： open access journal， 2017， 12（5）：555864.

[13] PEREIRA T D，ALDARONDO D E，WILLMORE L，et al.Fast animal pose estimation using deep neural networks[J]. Nature methods， 2019， 16（1）： 117-125.

[14] CUI R， LIU H， ZHANG C. A deep neural framework for continuous sign language recognition by iterative training[J]. IEEE Transactions on Multimedia， 2019， 21（7）： 1 880-1 891.

[15] JAIN D K，SHAMSOLMOALI P，SEHDEV P.Extended deep neural network for facial emotion recognition[J].Pattern Recognition Letters，2019，120： 69-74.

[16] NASSIF A B， SHAHIN I， ATTILI I， et al. Speech recognition using deep neural networks： A systematic review[J]. IEEE Access， 2019， 7： 19 143-19 165.

[17] CHEN J，WANG G，GIANNAKIS G B.Graph multiview canonical correlation analysis[J].IEEE Transactions on Signal Processing， 2019， 67（11）： 2 826-2 838.

[18] WANG W，ARORA R，LIVESCU K，et al.On deep multi-view representation learning[C]//International Conference on Machine Learning.JMLR，org：Lille，

France，2015： 1 083-1 092.

（責任編輯：李 麗）