基于NSGA-Ⅲ的水資源多目標優化配置研究

王一杰 王發信 王振龍 索梅芹 陳小鳳 董國強

摘要：優化配置、高效利用區域內有限水資源仍是當今研究熱點。以安徽省泗縣為典型研究區，以經濟效益最大、社會缺水量最小和污染物排放量最小為目標函數，建立了泗縣水資源多目標優化配置模型;采用NSGA-Ⅲ算法求解，生成了Pareto最優解集。選擇4種側重點不同的水資源配置方案，即方案一側重于經濟效益、方案二側重于社會效益、方案三側重于生態環境效益、方案四側重于綜合效益，來研究以協調水資源、經濟社會和生態環境之間的關系，最終實現綜合效益最大化的目標。研究結果表明：方案四為優選方案，該方案的配水總量為22 663萬 m3，經濟效益為325億元，余水量為101萬 m3，污染物排放量為1 969 t。研究成果可為安徽省泗縣水資源合理配置提供科學依據。

關 鍵 詞：

多目標優化配置; 水資源優化配置; NSGA-Ⅲ算法; 泗縣; 安徽省

中圖法分類號： TV212.4

文獻標志碼： A

DOI：10.16232/j.cnki.1001-4179.2021.05.012

水是生產之要、生態之基、生命之源，在人類社會發展中具有重要地位。現階段，區域水量短缺、

水質惡化等問題嚴重制約著經濟社會的可持續發展。為此，開展研究區域水資源優化配置研究，科學合理地分配有限的水資源量，能夠有效緩解水資源短缺帶來的壓力。目前，國內外學者已有多種水資源優化配置模型和各種求解方法，并取得了豐碩成果。李宗禮等[1]以石羊河流域為研究對象，建立了該區域多目標水資源優化配置模型，研究得到了生產、生活和生態綜合效益最大化的配置方案;王宏偉等[2]以西寧市為研究對象，建立了該區域多目標水資源優化配置模型，并采用多目標遺傳算法求解;王永濤等[3]建立了黔中工程水資源優化配置模型，并采用多目標規劃來求解模型;靳玉瑩等[4]先利用層次分析法對承德市的水權進行分配，然后在社會效益、經濟效益和生態效益目標下對水權分配方案進行優化;吳云等[5]建立了山西“大水網”晉中-長治供水區水資源多目標優化配置模型，并對NSGA-II算法在約束條件和遺傳操作方面進行了改進。

目前學者對于采用NSGA-Ⅲ算法進行水資源優化配置方面的研究不多。本文以安徽省泗縣為研究區域，利用NSGA-Ⅲ算法，建立多目標水資源優化配置模型;以經濟效益最大、社會缺水量最小和污染物排放最小為目標函數，對研究區域內的生活、生產和生態環境之間用水尋求水量最優分配，以此保障該區域水資源的可持續利用，實現經濟、社會和生態環境綜合效益最大化。

1 研究區域概況

泗縣位于安徽省東北部，東經117°37′～118°11′，北緯33°16′～33°46′。研究區域的多年平均降水量為865.9 mm，年內降雨分布不均，60%～70%的降水集中在汛期（6～9月），極易形成集中暴雨;降水年際變化大，豐枯交替出現。根據泗縣統計年鑒和水資源公報，現狀年全縣戶籍人口96.11萬人，地區生產總值（GDP）達231.3億元（當年價）。總用水量為17 500萬 m3，其中農業用水量為10 860萬 m3，工業用水量為2 965萬 m3，居民生活用水量為3 407萬 m3（含城鎮公共用水），生態環境用水量268萬 m3。供水總量為17 500萬 m3，其中地表水源供水量為7 175萬 m3，地下水源供水量為9 990萬 m3，再生水源供水量為335萬 m3。

由于該區域地處平原區，境內缺乏大規模蓄水工程，雨洪資源難以得到充分利用，使得地表水資源總體開發利用率較低，且境內地表水水質整體較差。因境內外調水滯后，致使該區域長期依托開采地下水資源來維持社會經濟發展。目前，由于地下水長期超采已導致地下水位持續下降，城區及其近郊已形成了32 km2的地下水超采區。

綜上所述，泗縣水資源為資源型、工程型和水質型缺水并存地區，水資源天然稟賦條件較差。因此，為了高效利用有限的地表水資源，合理開采地下水資源，充分利用再生水資源，亟需開展該區域水資源優化配置研究，以期為泗縣水資源規劃管理提供理論依據。

2.3 模型參數確定

（1） 需水量和可供水量預測。

規劃年需水量預測主要采用定額法，定額標準參考《安徽省用水定額》，并結合泗縣現狀年用水定額及未來發展趨勢進行綜合確定，預測結果如表1所列。規劃年供水水源主要為地表水、地下水和再生水。在P=75%水文年下可供水量如表2所列。

（2） 凈效益系數。

各目標效益系數的確定可參考文獻[6-9]。根據“優先保障居民生活用水”的原則，結合研究區域過去和現階段經濟社會的發展狀況，并綜合考慮未來的發展趨勢，生活用水凈效益系數應取一個較大值，因此確定生活用水凈效益系數為348.0元/m3;工業用凈效益系數根據研究區域萬元產值用水量和工業用水水價來確定，工業用水凈效益系數為197.0元/m3;農業用水凈效益系數根據農業增加值、水利分攤系數和農業用水水價確定，農業用水凈效益系數為10.8元/m3;考慮生態環境和居民生活息息相關，故生態用水凈效益系數取348.0元/m3。

（3） 配水關系。考慮地下水資源為優質水源，故地下水資源不供給生態用水;再生水因水質和供水成本因素，不供給生活和農業用水。配水關系如表3所列。

（4） 污染物排放濃度、污染物排放系數、污染物允許排放量。對此，需綜合考慮研究區域污水處理工藝、水質管理目標和水域納污能力等因素加以確定。具體參數如表4所列。

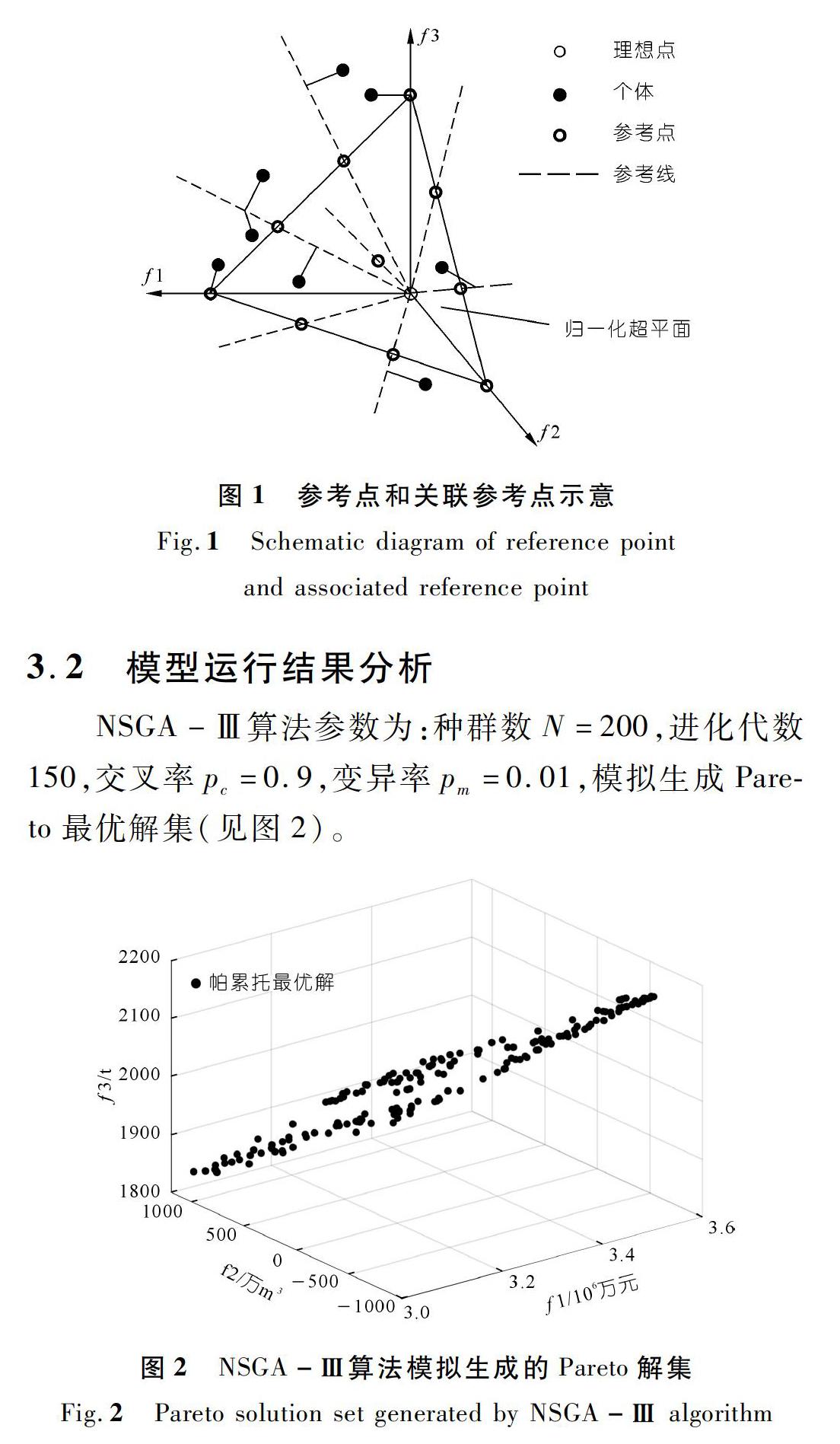
（5） 關聯參考點。

構建參考點向量（參考點到原點連線即為一條參考向量），計算種群D中每個個體到參考線的垂直距離，若種群中某一個體與參考線距離最短，則認為該參考點與個體相關聯，如圖1所示。

（6） 篩選子代與刪除參考點。

經非支配排序后，若從第一個支配層F1到第Fl層級種群數目總和第一次超過N，則篩選第一步為遍歷每個參考點，尋找被引用次數最少的參考點，即被最少的種群個體所關聯的參考點，其被引用次數記錄為ρj。若ρj=0，但在Fl中有個體被關聯到這個參考點向量，則從Fl支配層中選擇到該參考點距離最小的點，加入到被選擇的下一代種群中，設置ρj=ρj+1;若ρj≥1，且Fl支配層中沒有個體被引用到該參考點，則刪除該參考點向量[13-14]，重復上述操作直到種群規模為N。

3.2 模型運行結果分析

NSGA-Ⅲ算法參數為：種群數N=200，進化代數150，交叉率pc=0.9，變異率pm=0.01，模擬生成Pareto最優解集（見圖2）。

上述模型運行后即可求得Parto最優解集。根據多目標優化的模型具有以下特點：

（1） 在多目標規劃中，各子目標之間相互矛盾、相互沖突，且某一子目標的優化是以犧牲其他子目標來實現（如追求經濟效益最大化的同時，勢必會對生態環境造成更多污染）。

（2） 因多目標規劃解不惟一，是多個解組成的非劣解集，根據決策者偏好，可選擇其滿意的解，不同決策者有不同的偏好，因此，根據優化結果，選擇了4種優化配置方案以供決策者選擇。即：方案一側重于經濟效益最大;方案二側重于社會效益，即區域缺水量最小;方案三側重于生態環境效益，即區域污染物排放量最小;方案四側重于綜合效益。優化配置結果如表5所列。

方案一的地表水配水量為4 976萬m3，地下水的配水量為17 930萬m3，再生水的配水量為600萬m3;方案二的地表水配水量為4 152萬m3，地下水的配水量為16 837萬m3，再生水的配水量為623萬m3;方案三的地表水配水量為4 069萬m3，地下水的配水量為16 870萬m3，再生水的配水量為589萬m3;方案四的地表水配水量為4 088萬m3，地下水的配水量為17 888萬m3，再生水的配水量為687萬m3。其中，方案一對地下水的開采量最高，方案四對地表水資源和再生水的利用量最高。

方案一的配水總量為23 506萬m3，經濟效益為355億元，缺水量為783萬 m3，污染物排放量為2 174 t;方案二的配水總量為21 529萬m3，經濟效益為305億元，余水量為1 111萬 m3，污染物排放量為1 832 t;方案三的配水總量為21 528萬 m3，經濟效益為304億元，余水量為1 105萬 m3，污染物排放量為1 825 t;方案四的配水總量為22 663萬 m3，經濟效益為325億元，余水量為101萬 m3，污染物排放量為1 969 t，其中方案一的配置水量最高。不同方案層的各目標效益值列于表6。

綜合4種決策方案，可以看出：

（1） 在方案一下，區域經濟可得到最大化發展，但用水部門存在一定程度的缺水現象，社會效益得不到滿足，而且在該決策方案下區域污染物排放量最大。

（2） 在方案二下，全區域用水均可得到滿足，總用水量較低，不會出現缺水現象，而且污染物排放量也較小。但在該方案下，區域經濟效益較低。

（3） 在方案三下，優化配置結果和各目標效益均與方案二的相似。

（4） 在方案四下，強調各子目標之間的協調發展，統籌考慮各子目標，不偏否任一子目標，以區域用水綜合效益最大化為目標。

根據泗縣政府相關政策，規劃年應減小對地下水的開采量，加大對再生水的利用量和地表水的利用量等，因此推薦方案四為最優方案。

3.3 模型優劣性和實用性分析

基于可持續發展理念和新的治水方針，在水資源“三條紅線”保護下，水資源多目標優化規劃越來越符合現代水行政部門的管理方法，該方法能夠較好地處理配水中多個相互矛盾、相互沖突的目標。通過采用NSGA-Ⅲ算法來求解該模型，由生成的Pareto最優解集（見圖2） 可知：該方法能夠保持Pareto最優解集分布的多樣性，同時還具有良好的收斂性和適應性。若規劃年間，區域用水部門、供水水源等發生變化，即可通過修改、調試模型參數而求得優化配置結果，因此具有較強的可操作性和實用性。

4 結 論

（1） 針對安徽省泗縣地區水資源現狀，綜合考慮到供水水源和用水部門的供需關系，建立了以經濟效益最大、區域缺水量最小和污染物排放量最小的多目標水資源優化配置模型，并采用NSGA-Ⅲ算法來求解模型，計算結果具有多樣性。

（2） 與其他3種方案相比，方案一在追求經濟效益最大化的同時，區域內存在一定程度的缺水，對生態環境造成了較大污染;方案二和方案三的水量分配大致相同;方案四的水資源供需基本平衡，在保證經濟社會發展的同時，減少了對生態環境污染。方案四為推選方案，其結果為經濟-社會-生態環境綜合效益最優，該方案的配水總量為22 663萬m3，經濟效益為325億元，余水量為101萬 m3，污染物排放量為1 965 t。

（3） NSGA-Ⅲ算法在水資源優化配置中的應用較少，實例計算結果表明，模擬生成的Pareto最優解集收斂性較好，而且Pareto最優解集分布較為均勻，取得了滿意的計算結果。該算法可為多目標水資源優化配置的求解提供新的途徑。

本文沒有針對研究區考慮多水源、多要素、多約束在更大區域上的應用進行研究，因此有待開展進一步的研究。

參考文獻：

[1] 李宗禮，李新攀，趙文舉，等.基于多目標遺傳算法的石羊河流域水資源優化配置模型[J].蘭州理工大學學報，2013，39（2）：52-55.

[2] 王宏偉，張鑫，邱俊楠，等.基于多目標遺傳算法的西寧市水資源優化配置研究[J].水土保持通報，2012，32（2）：150-153.

[3] 王永濤，楊璐瑤，張和喜，等.基于多目標優化的黔中區水資源配置研究[J].人民長江，2017，48（1）：32-36.

[4] 靳玉瑩，趙勇，張金萍，等.基于多目標優化模型的承德市初始水權分配[J].水電能源科學，2017，35（1）：156-159.

[5] 吳云，曾超，楊侃，等.基于改進NSGA-Ⅱ算法的水資源多目標優化配置[J].人民黃河，2020，42（5）：71-75.

[6] 趙燕，武鵬林，祝雪萍.基于改進螢火蟲算法的水資源優化配置[J].人民黃河，2019，41（5）：62-66.

[7] 辛朋磊，陳建標.基于全局優化的南通市水資源優化配置研究[J].人民長江，2012，43（17）：55-60.

[8] 張玲玲，高亮.多目標約束下區域水資源優化配置研究[J].水資源與水工程學報，2014，25（4）：16-19.

[9] 張芮，喬延麗，祿芳霞，等.基于多目標模糊優化模型的蘭州市水資源優化配置研究[J].節水灌溉，2016（2）：59-62.

[10] DEB K，JAIN H.An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach，Part I：Solving Problems With Box Constraints[J].IEEE Transactions on Evolutionary Computation，2014，18（4）：577-601.

[11] 蔣寧，范偉，謝小東，等.NSGA-Ⅱ和NSGA-Ⅲ應用于換熱網絡多目標優化的對比[J/OL].化工進展：1-19[2020-06-19].https：//doi.org/10.16085/j.issn.1000-6613.2019-1466.

[12] 吳偉麗.基于NSGA-Ⅲ的復雜成因變壓器直流偏磁控制優化算法[J].電測與儀表，2018，55（11）：89-93.

[13] 丁圣.基于NSGA-Ⅲ的列車多目標操縱優化研究[D].北京：北京工業大學，2018.

[14] 畢曉君，王朝.一種基于參考點約束支配的NSGA-Ⅲ算法[J].控制與決策，2019，34（2）：369-376.

（編輯：趙秋云）