曳引式電梯垂直振動分析

嚴文磊 薛大猛

1鹽城工學院 鹽城 224000 2希姆斯電梯（中國）有限公司 無錫 214000

0 引言

根據國家市場監管總局特種設備局統計，截至2019年底，注冊在運行的電梯總量達到709.75萬臺，當年新增81.92萬臺。電梯已經同人們日常生活息息相關，成為不可缺少的一部分。

振動加速度是電梯乘運質量的關鍵評價指標之一，GB/T 10058—2009《 電梯技術條件3.3.5中規定乘客電梯轎廂運行在恒加速度區域內的垂直（Z軸）振動的最大峰峰值不應大于0.3 m/s2，A95峰峰值不應大于0.2 m/s2。本文通過對試驗塔內某臺電梯進行動力學分析，找出影響振動加速度的關鍵因素。

1 動力學建模

試驗塔內電梯梯速為2.5 m/s，額定載重為1 600 kg，曳引比為2:1，轎廂質量為750 kg，轎架質量為700 kg，對重質量為2 250 kg，曳引機質量為480 kg，鋼絲繩根數為7根，直徑為0.01 m，線密度為0.407 kg/m，彈性模量為8×1010Pa，繩頭彈簧剛度為2.12×105N/m，轎底減震橡膠剛度為5×105N/m，曳引輪，對重輪和導向輪直徑為0.4 m。其結構見圖1。

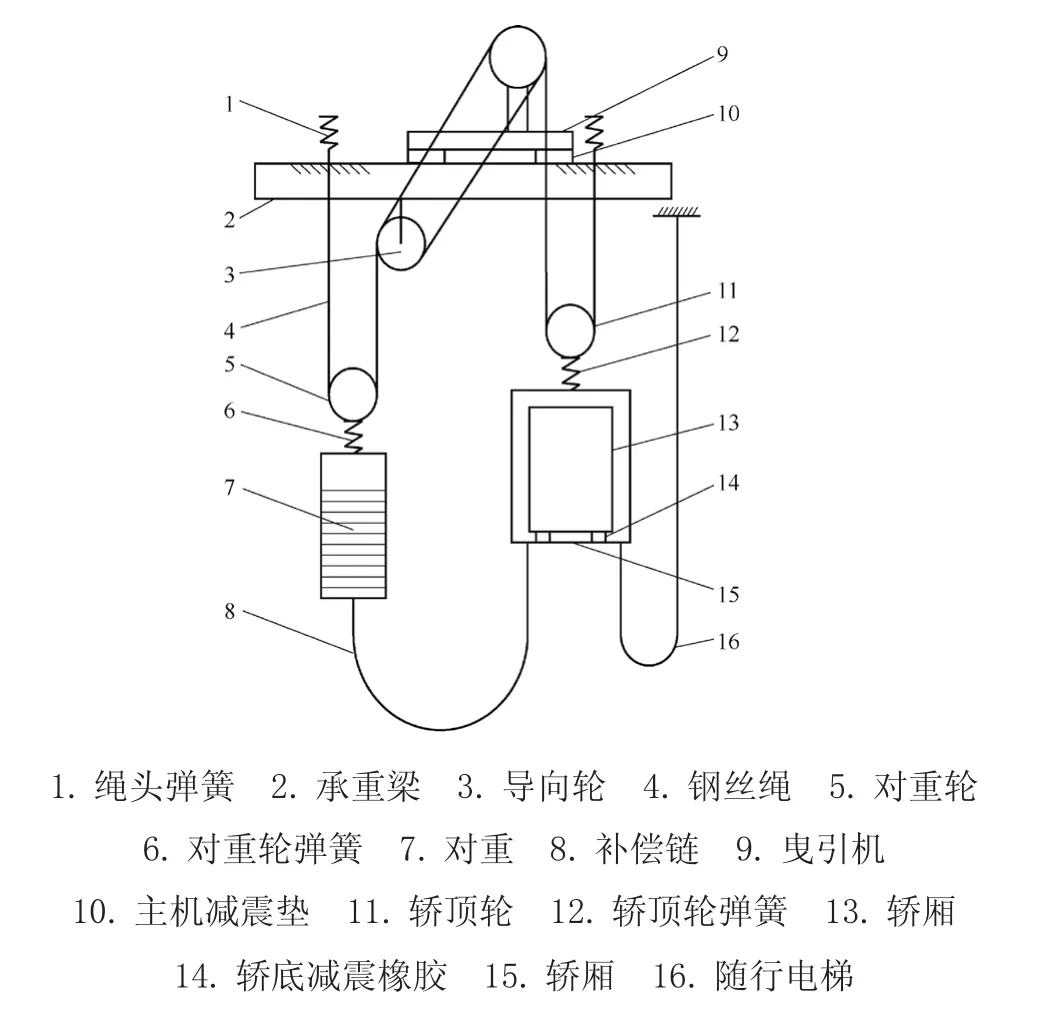
圖1 電梯結構示意圖

假定位移向上為正方向，角位移逆時針為正，對電梯建立動力學模型，其動力學模型見圖2。

圖2 電梯動力學模型

在圖2中，m1為轎廂和額定載荷質量，m2為轎架和部分補償鏈、隨行電纜等效質量，m3為對重和部分補償鏈等效質量，m4為曳引機和導向輪等效質量，I1為曳引輪和導向輪等效轉動慣量，r1為曳引輪半徑，m5轎頂輪和鋼絲繩等效質量，I2為轎頂輪轉動慣量，r2為轎頂輪半徑，m6為對重輪和鋼絲繩等效質量，I3為對重輪轉動慣量，r3為對重輪半徑，k1為轎底減震橡膠等效剛度，c1為轎底減震橡膠阻尼，k2為轎頂輪彈簧等效剛度，c2為轎頂輪彈簧阻尼，k3為對重輪彈簧等效剛度，c3為對重輪彈簧阻尼，k4為承重梁和主機減震墊等效剛度，c4為承重梁和主機減震墊阻尼，kr1為轎頂輪到繩頭彈簧之間鋼絲繩和繩頭彈簧的等效剛度，cr1為轎頂輪到繩頭彈簧之間鋼絲繩和繩頭彈簧的阻尼，kr2為轎頂輪到曳引機之間鋼絲繩等效剛度，cr2為轎頂輪到曳引機之間鋼絲繩阻尼，kr3為對重輪到曳引機之間鋼絲繩等效剛度，cr3為對重輪到曳引機之間鋼絲繩阻尼，kr4為對重輪到繩頭彈簧之間鋼絲繩和繩頭彈簧的等效剛度，cr4為對重輪到繩頭彈簧之間鋼絲繩和繩頭彈簧的阻尼，kT為曳引機的扭轉剛度，cT為曳引機阻尼。

參考文獻[2]認為，當電梯提升高度大于50 m時，鋼絲繩自重對垂直振動影響較大，需要考慮其質量，而當提升高度較低時，鋼絲繩質量可以忽略不及。參考文獻[3]通過計算發現，將鋼絲繩離散成4段可以得到較為穩定的結果。為了考慮鋼絲繩的質量，同時減少模型的自由度，本文通過對鋼絲繩分布質量作近似計算，得到其等效質量。

設鋼絲繩的長度為l，單位長度的質量為p，假定鋼絲繩的變形與固定點的距離ξ正比，鋼絲繩端點的位移為x，將微元長度dξ的動能在整個鋼絲繩長度范圍內積分，以計算鋼絲繩的動能

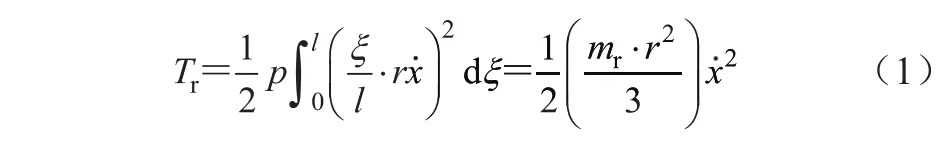
式中：mr為鋼絲繩質量，mr＝pl，r為曳引比，mrr2/3為鋼絲繩的等效質量，將其加到轎頂輪或對重輪上。鋼絲繩分布質量系統見圖3。

圖3 鋼絲繩分布質量系統

此外，參考文獻[2]認為，曳引機－曳引輪之間為完全剛性傳動，故曳引輪的扭轉剛度為0。由于在模型中需使用此參數，整個系統會存在剛體模態，在矩陣分解時會造成計算困難，故取一個很小的數值。參考文獻[3]認為當電梯采用有齒輪曳引機時，在曳引機輸出軸到曳引輪軸之間有蝸輪蝸桿減速器，故兩者之間非剛性傳動，存在扭轉剛度。當今的電梯中多采用永磁同步無齒輪曳引機，曳引機輸出軸與曳引輪軸直接相連，沒有減速器，故該過程可看作剛性傳動，扭轉剛度為0。為了避免計算困難，同樣賦予其很小的數值。參考文獻[5]認為，在電梯建模仿真過程中，如果抱閘處于釋放狀態，曳引輪可自由轉動，故扭轉剛度看作0。因此，在本文中的扭轉剛度取10-6Nm/deg。

根據拉格朗日方程可得

式中：T為系統的動能，V為系統的勢能，xi為系統第i個自由度的廣義位移，為系統第i個自由度的廣義速度，Qi為系統第i個自由度的廣義力。

其中，系統的動能為

系統的勢能為

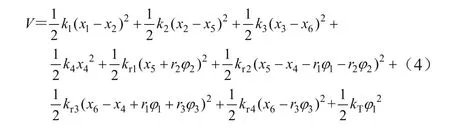
經過簡化可以得到系統動力學方程

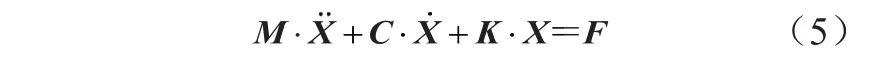
式中：M為系統的質量矩陣，C為系統的阻尼矩陣，K為系統的剛度矩陣，F為系統的激勵力列陣，X··為系統的廣義加速度列陣，X·為系統的廣義速度列陣，X為系統的廣義位移列陣。

由式（3）和式（4）得

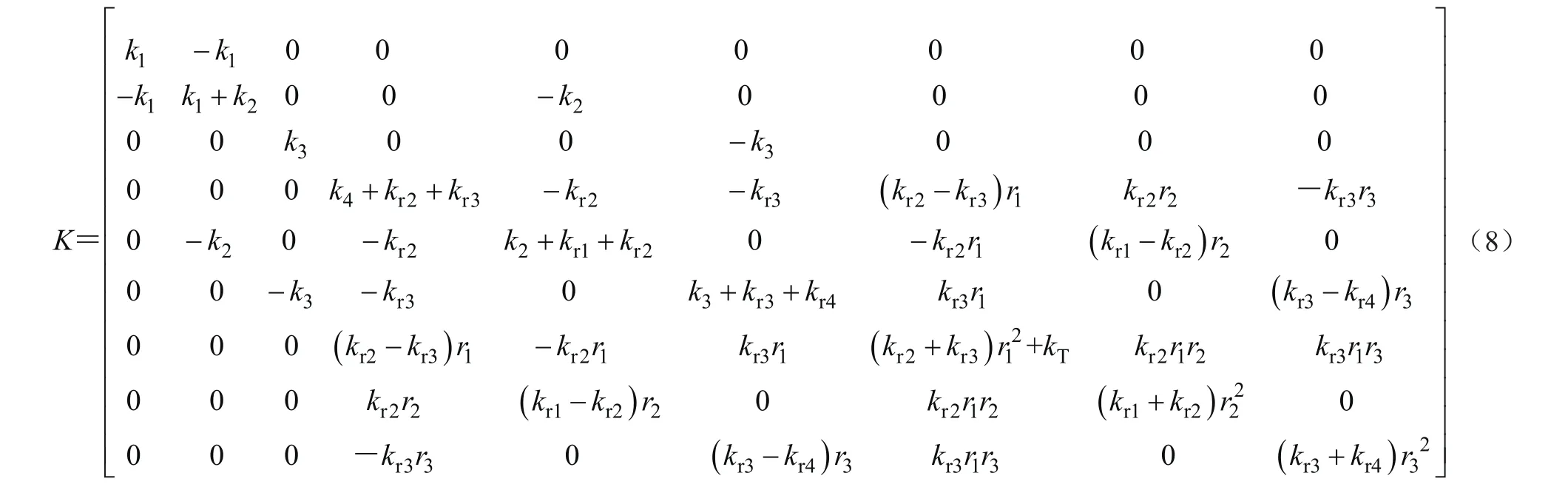
在工程中，電梯的實際阻尼難以測量，考慮到電梯為小阻尼機械系統，采用Rayleigh阻尼模型進行等效

式中：ac、bc為阻尼系數，參照文獻[6]，取ac=0.01，bc=0。

考慮電梯系統運行中的慣性力和慣性力矩，曳引輪，對重輪、導向輪的旋轉失衡，激勵力列陣見式（10）。根據文獻[7]中曳引輪偏心實驗，將曳引輪偏心質量近似看作為1 kg，偏心距為0.15 m，轎頂輪及對重輪偏心質量近似看作為0.2 kg，偏心距為0.15 m。

式中：mt為曳引輪轉子偏心質量，mj為轎頂輪轉子偏心質量，md為對重輪轉子偏心質量，ωt為曳引輪轉動角速度，ωj為轎頂輪轉動角速度，ωd為對重輪轉動角速度；et為曳引輪偏心距，ej為轎頂輪偏心距，ed為對重輪偏心距，a為轎廂運行加速度。

2 模態分析

無外力作用的多自由度系統受到初始擾動后，即產生自由振動。其方程為

此方程的特解為

其中，Ф＝（φi）為各坐標振幅組成的n階列陣，此特解表示系統內各個坐標偏離平衡值時均以同一頻率ω和同一初相角θ做不同振幅的簡諧運動。

系統的固有頻率和振型化為矩陣K和M的廣義特征值和特征向量的問題，即

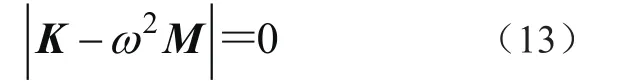
由于電梯垂直方向動力學系統的平衡位置是隨遇的，故主振動存在隨時間無限增大的剛體位移。顯然，系統的第一階固有頻率ω1＝0。通過模態分析，可求出電梯垂直振動系統的固有頻率，從而避免外激勵的頻率與固有頻率相同而形成共振。

在電梯空載時，求得二～六階固有頻率隨時間的變化如圖4～圖8所示。

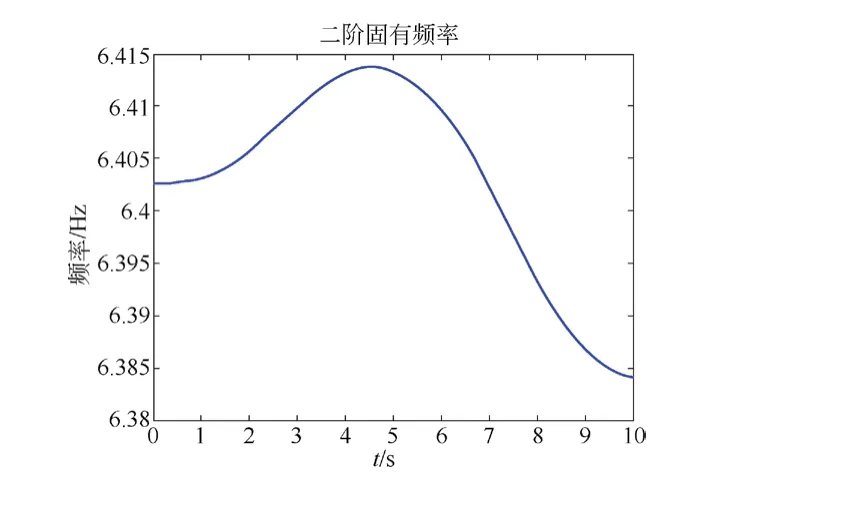
圖4 空載電梯二階固有頻率

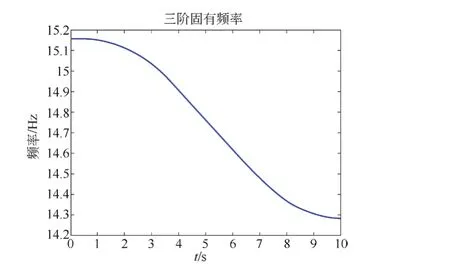
圖5 空載電梯三階固有頻率

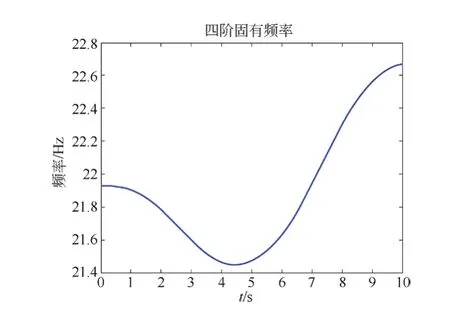
圖6 空載電梯四階固有頻率

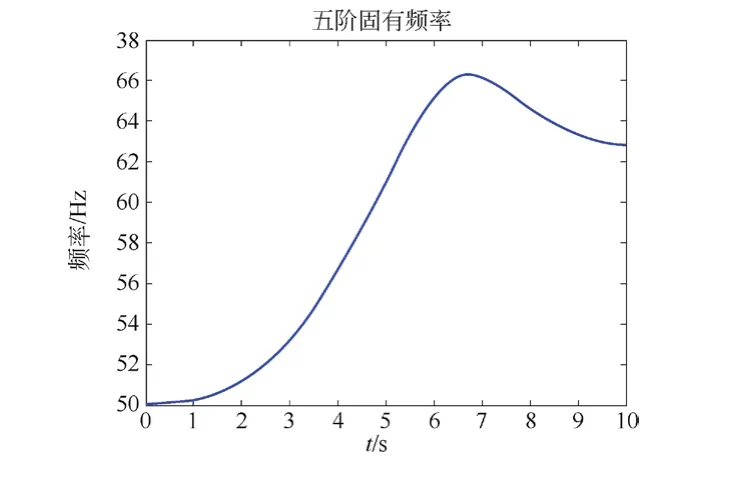
圖7 空載電梯五階固有頻率

圖8 空載電梯六階固有頻率

隨著電梯上升，二階固有頻率從6.4 Hz先上升再下降，波動幅度約為0.5 Hz；三階固有頻率從15.1 Hz開始降低，降低幅度約為1 Hz；四階固有頻率從21.9 Hz先下降再上升，波動幅度約為1 Hz；五階固有頻率從50 Hz先上升再下降，波動幅度約為16 Hz；六階固有頻率從151 Hz開始先下降再上升，波動幅度約為60 Hz。

電梯二～四階固有頻率隨著電梯上升波動幅度不大。從第五階固有頻率開始，波動范圍大幅增加。在此系統中，曳引機振動頻率約為3.98 Hz，故不會出現曳引機振動引起共振的情況。

3 動力學方程求解

對多自由度動力學方程的求解方法有多種，一般做法是將多自由度方程通過坐標變化解耦成單自由度方程，再基于振型疊加法使用杜哈梅積分求解，但這種解法繁瑣且計算量大，本文中將通過Newmark-β法對多自由度方程求解。

Newmark-β法是一種數值分析方法，其基本原理是將時間離散化，在時間增量內假定加速度變化規律計算結構動力響應[8]。假設在ti和ti+1時刻的加速度值某一常量，記為a。有

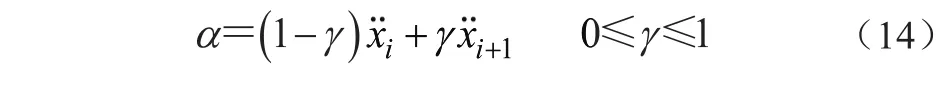
為得到穩定和高精度的算法，α也用另一控制參數β表示，即

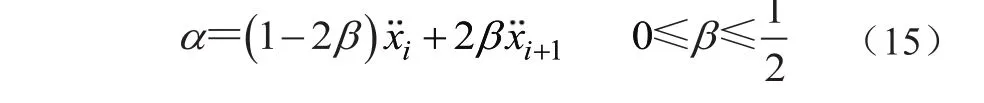
通過在ti到ti+1時間段上對加速度積分，可得ti+1時刻的速度和位移

將式（14）代入式（16），式（15）代入式（17）得

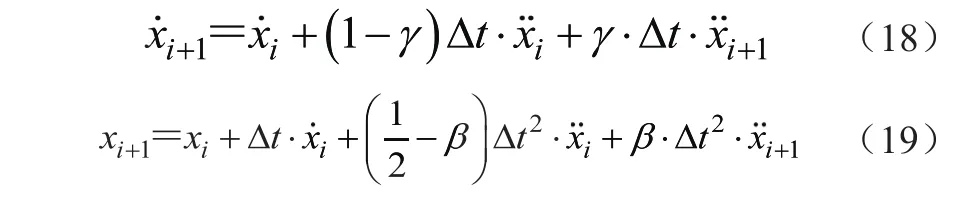
式（18）、式（19）為Newmark-β的兩個基本遞推公式，可解得ti+1時刻的速度和加速度的計算公式，即

由式（20）和式（21）所示的運動滿足ti+1時刻的運動控制方程為

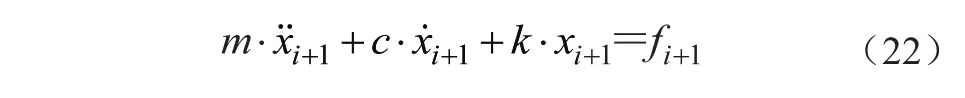
將式（20）和式（21）代入式（22）得ti+1時刻位移xi+1得計算公式為

其中

在Newmark-β法中，控制參數β和γ的取值影響算法的精度和穩定性，可以證明，只有當γ＝1/2時，該方法才具有二階精度，故一般取γ＝1/2，β＝1/4。

4 測量及分析

使用EVA-625檢測儀對試驗塔內電梯進行測試，其轎廂實際速度和加速度曲線見圖9、圖10。

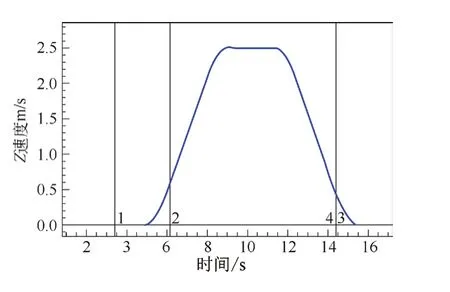
圖9 實測速度曲線

由圖10可知，電梯由啟動到制停共分為7個時間段。其中，0～t1時刻，加速度a從0上升到最大值am；t1～t2時刻，加速度a保持恒定；t2～t3時刻，加速度a由am下降至0；t3～t4時刻，加速度a保持為0；t4～t5時刻，加速度a由0下降至-am；t5～t6時刻，加速度a保持為-am；t6～t7時刻，加速度a～-am上升至0。其中je為加加速度，vm為速度最大值[9]。電梯轎廂的速度和加速度可表示為

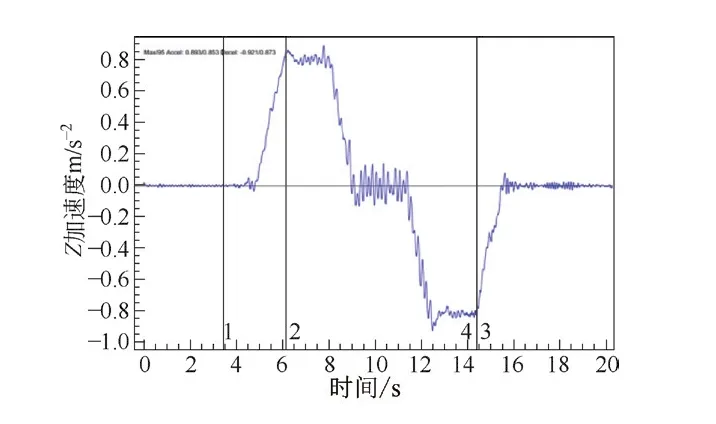
圖10 實測加速度曲線

當je＝0.8 m/s3、am＝ 0.8 m/s2、vm=2.5 m/s時，模型的速度和加速度曲線見圖11和圖12。

圖11 模型速度曲線

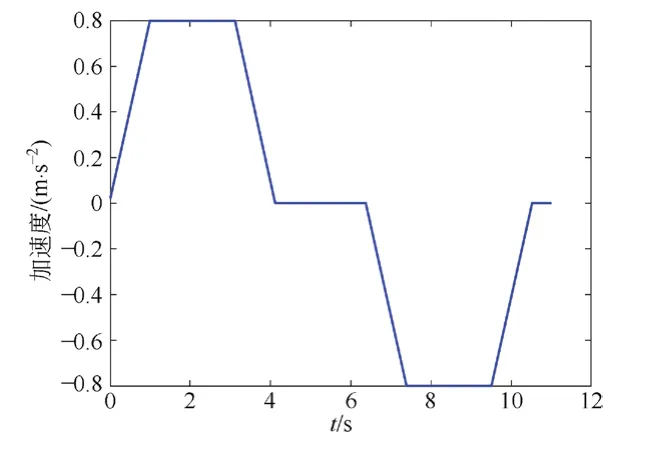
圖12 模型加速度曲線

電梯轎廂在運行過程中，通過EVA-625檢測儀對其垂直（Z軸）振動進行檢測。其原始Z軸信號見圖13。

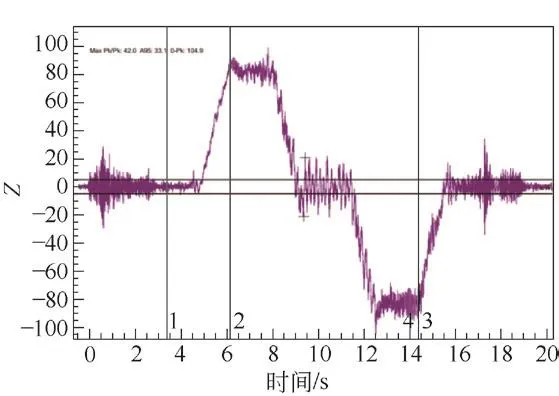
圖13 原始Z軸信號

由圖13可知，電梯啟制動前后一段時間內，開關門機對信號影響甚大，應予以忽略。根據GB/T 24474—2009《電梯乘運質量測量》5.2.1中規定[10]：加速度和減速度值應通過對原始Z軸信號進行10 Hz低通濾波后計算。其濾波后的信號見圖14。

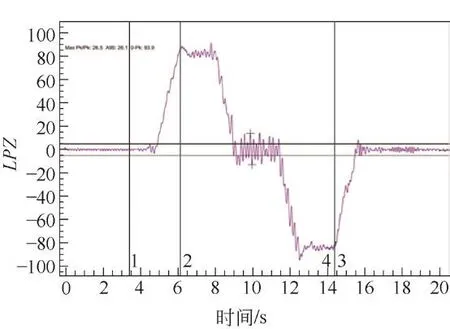
圖14 10 Hz濾波后Z軸信號

由圖14可知，可知其振動加速度最大峰峰值為0.265 m/s2，A95 峰峰值為 0. 261 m/s2。

EVA-625檢測儀有3種濾波方式：ISO、高通和低通。其中ISO濾波器是振動分析中最有力的一個工具。ISO濾波器會依據IS08041標準將測試數據處理成標準中描述的人類能感受的垂直和水平方向的振動[11]。經過ISO濾波后的振動曲線如圖15所示。

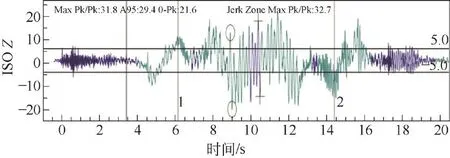
圖15 ISO濾波垂直（Z軸）振動曲線

對經過ISO濾波后的最大峰峰值進行FFT（快速傅里葉轉換）分析，可以得到振動的振幅和頻率數據信息，快速傅里葉轉換后見圖16。為對比不同速度對電梯垂直系統固有頻率的影響，在其他條件不變的情況下，將速度從2.5 m/s改為1.75 m/s，其最大峰快速傅里葉轉換后見圖17。

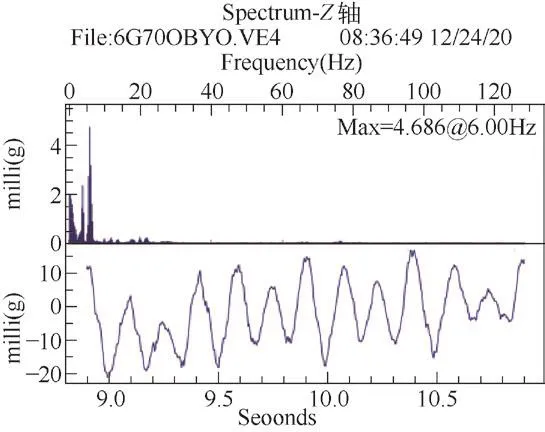
圖16 2.5 m/s最大峰快速傅里葉轉換

從圖16和圖17可以看出，對振幅影響最大的頻率為6 Hz，與上文模態分析中系統的第二階模態基本吻合，并且不隨速度而變化。在圖16中，頻率4 Hz對振幅影響較大，這是曳引機振動的頻率。此外的一些低頻信號，可能是由電梯系統變剛度引起的自激振動[12]，也可能由電梯運行時空氣阻力引起的振動[13]。

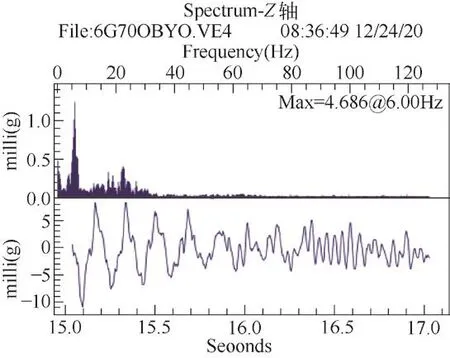
圖17 1.75m/s最大峰快速傅里葉轉換

通過Newmark-β法對動力學方程進行求解，可知其振動加速度峰值約為0.3 m/s2，高出實際測量值12%左右。模型中峰值加速度出現在變減速開始的階段，而實測中峰值加速度出現在變加速結束的階段，兩組值相差不大。經過多次實驗，發現其峰值加速度出現的位置很大程度上取決于現場實際情況。考慮到計算時做了部分假設和簡化，故其值在實際工程中可以接受。Newmark-β法振動曲線見圖18。

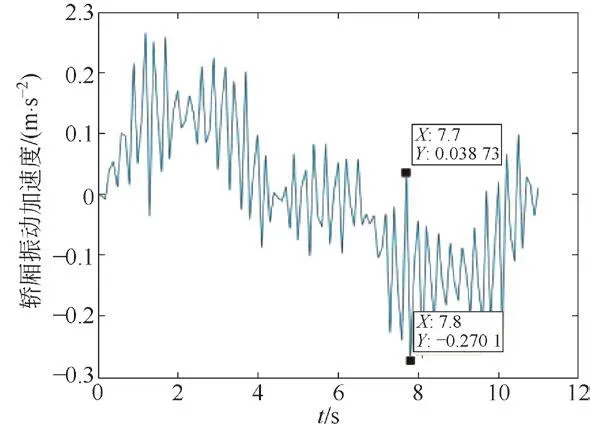
圖18 Newmark-β法計算振動曲線

5 結論

綜上所述，在不同速度下電梯系統的基頻是不變的，且為振動的最主要成分。若基頻發生變化，可能是電梯發生共振所致。當電梯發生共振時，可通過改變減震墊和繩頭彈簧等的剛度改變系統固有頻率以避免共振。

通過更改模型的參數，可知當曳引比為2:1時，反繩輪中存在的偏心質量，將對振動加速度產生相當大的影響；降低鋼絲繩的彈性模量，可整體降低振動加速度；適當增加轎廂或者轎架的質量可有效降低振動加速度。