局部減薄管道極限彎矩計算新公式

李祚成，李思源，許 可

（1.機械工業上海藍亞石化設備檢測所有限公司，上海 201518；2.蘭州石油機械研究所有限公司，甘肅 蘭州 730050；3.中石油 云南石化有限公司，云南 昆明 650300）

壓力管道，特別是海底管道，由于使用環境復雜、管道承受的載荷復雜、管道的應力狀態復雜，因此管道剩余強度的評估也是一個復雜的課題。近半個世紀以來，國際上對管道剩余強度評估開展了許多的硏究工作，其中Bouwkamp J G等[1]和Sherman D R[2]對無缺陷管道在聯合載荷下的極限承載力進行了大量的數值分析和實驗硏究。基于塑性失效理論，釆用理想彈塑性本構模型，Mohareb M等[3-8]提出了無缺陷管道在內壓、軸向力和彎矩聯合載荷下的極限承載力解析解，并與實驗結果進行比較，得出該簡化方法能很好地預測管道極限承載力。之后Bai Y等[9-12]將這部分工作擴展到了腐蝕管道，將管道腐蝕形狀簡化為減薄深度在環向不發生變化，分別針對4種不同工況的等深減薄管道提出了極限彎矩計算方法。該方法已經被ABS的 《Guide for Building and Classing Subsea Pipeline System》[13]采用，用于評估腐蝕海底管道剩余強度。文獻[14-15]也釆用Hill屈服準則，推導了不規則腐蝕缺陷管道在內壓、軸向力和彎矩聯合作用下極限承載力的廣義計算公式。但筆者認為，文獻[9-15]中提出的當管道進入全塑性狀態時，管道橫截面壓應力極限值 σcomp（或 σc）和拉應力極限值 σtens（或σt）的計算式值得進一步探討。

本文針對承受內壓p、軸向力F和彎矩M聯合作用的局部減薄管道，應用屈服準則，給出了管道橫截面彎曲壓縮側應力極限值和彎曲拉伸側應力極限值的計算式，導出了內壓p和軸向力F必須滿足的條件。并釆用理想彈塑性本構模型，推導了含等深減薄管道在聯合載荷作用下極限彎矩計算的新公式，證明了文獻[9-15]中極限彎矩計算式的理論依據不充分。

1 局部減薄管道極限彎矩計算基本理論

1.1 基本假定和簡化

（1）不考慮管道鋼材應變強化作用，釆用理想彈塑性應力-應變本構關系。

（2）在管道達到全塑性狀態前，管道的橫截面形狀不發生改變。

（3）在管道達到極限狀態時，塑性中性軸將管道橫截面分為彎曲壓縮和彎曲拉伸2個區域，管道截面達到相應的全塑性狀態。

1.2 局部減薄管道屈服準則

設管道的外半徑為Ro，管壁厚度為t，平均半徑 Rm=Ro-t/2，管道內壁存在深度為 d、環向截面夾角為2β的等深減薄缺陷 （圖1），其軸向長度很長。

圖1 含等深減薄管道橫截面幾何尺寸示圖

對于各向異性材料的管道，在內壓p、軸向力F和彎矩M聯合作用下發生屈服時，釆用Hill屈服準則可以得到：

式中，σz為管道軸向應力，σθ為管道環向應力，σzl為管道材料軸向屈服應力，σθl為管道材料環向屈服應力，MPa；α為各向異性系數，一般取α=σθl/（2σzl）[14]。

求解式（1）得到管道軸向應力σz的解：

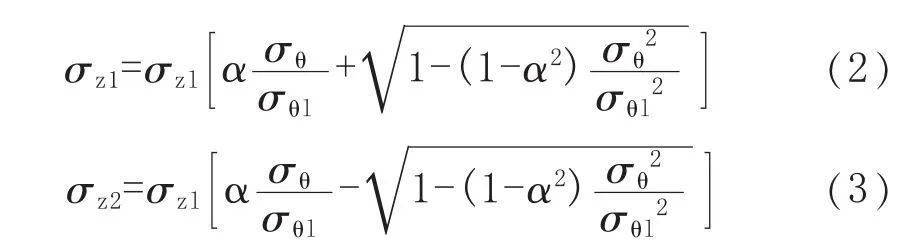
1.3 管道屈服的軸向極限應力

在內壓p、軸向力F和彎矩M聯合作用下，含等深減薄管道的環向應力σθ由內壓p、且只由內壓p產生，內壓p對該管道產生的軸向力Fp為軸向力F的組成部分。管道的軸向應力σz只由軸向力F和彎矩M產生。

1.3.1 等深減薄部位

在管道減薄深度為d的部位，管道的環向應力σθd由內壓p產生，且近似為：

當管道減薄深度為d的部位處于彎曲壓縮側時，將式（4）代入式（3），得到該部位屈服的軸向應力極限值σcd：

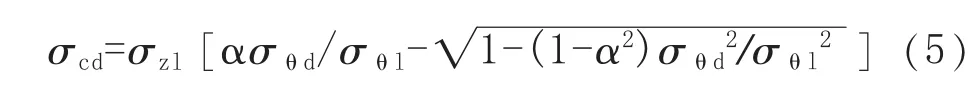
當管道減薄深度為d的部位處于彎曲拉伸側時，將式（4）代入式（2），得到該部位屈服的軸向應力極限值σtd：

1.3.2 未減薄部位

在管道未減薄部位，管道的環向應力σθ0由內壓p產生，且近似為：

當管道未減薄部位處于彎曲壓縮側時，將式（7）代入式（3），得到該部位屈服的軸向應力極限值 σc：

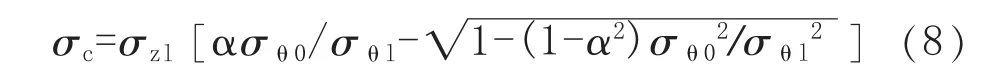
當管道未減薄部位處于彎曲拉伸側時，將式（7）代入式（2），得到該部位屈服的軸向應力極限值 σt：

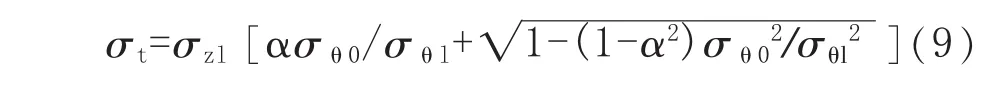
1.3.3 極限應力不等式

當管道內壓p＞0，管道等深減薄深度d＞0時，極限應力σcd和σc滿足不等式：

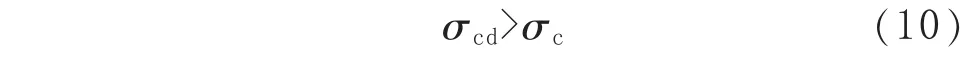
下面對式（10）進行證明。 由式（4）和式（7）可以得到：

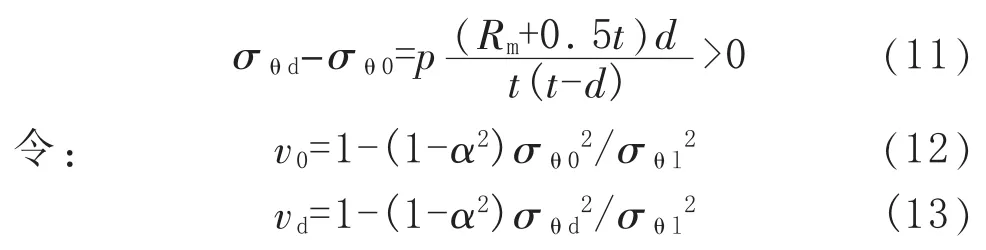
計及式（11），則有 v0-vd=(1-α2)(σθd-σθ0)×(σθd+σθ0)/σθl2＞0，因此有：

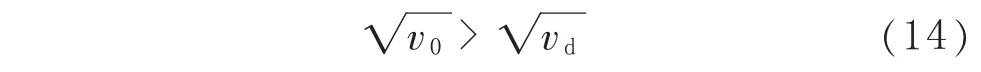
根據式（11）和式（14），由式（5）和式（8）可以得到：

由此可以證明式（10）成立。

2 等深減薄管道極限彎矩計算

2.1 等深減薄管道承載彎矩的條件

含等深減薄管道橫截面的面積 S（d，β）用式（16）計算：

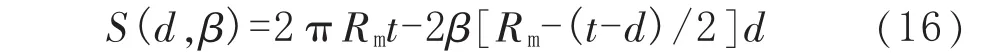
管道在內壓p和軸向力F聯合作用下，管道的軸向應力σz近似為：

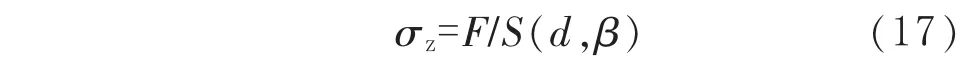
其中內壓p產生的軸向載荷包含在軸向力F當中。

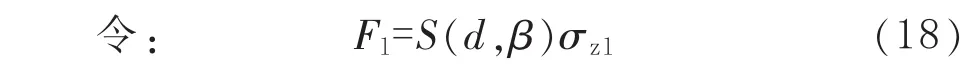
含等深減薄管道在內壓p和軸向力F聯合作用下，用式（4）計算減薄區的環向應力 σθd，用式（7）計算未減薄區的環向應力 σθ0，用式（18）計算Fl。該管道承載彎矩的條件是 σθd、σθ0和 F同時滿足以下不等式：

對式（19）進行證明。等深減薄管道在內壓p和軸向力F聯合作用下，管道產生的軸向應力σz可用式（17）近似計算，再應用式（18）得到：

亞行預計，氣候變暖在經濟方面將帶來負面影響。東南亞等國家如不及時采取措施，到本世紀末，氣候變化每年給相關國家帶來的經濟損失將超過GDP的5%以上，全球的GDP將下降2.8%，印度尼西亞、菲律賓將下降6.7%，比全球平均數高得多。相反，到2020年，若東南亞等國家增強應對全球氣候變化措施，增強能力建設，相應地投入一些成本，那么獲得的利潤比投入的成本要高得多。

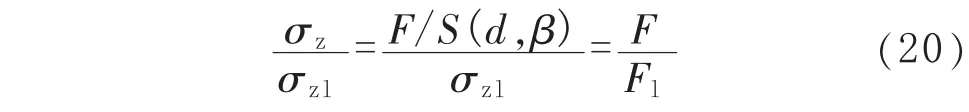
管道減薄區產生的環向應力σθ=σθd，應用式（20）有：

再利用式（19）中的第1式，得到在管道的等深減薄區都滿足：

管道未減薄區產生的環向應力σθ=σθ0，應用式（20）得到：

再利用式（19）中的第 2式，得到式（21）在管道的未減薄區也成立。

因此，等深減薄管道在內壓p和軸向力F聯合作用下沒有屈服，該管道還可以承載一定的彎矩載荷。

2.2 等深減薄管道極限彎矩計算新公式

2.2.1 計算工況

根據承載彎矩的條件，計算等深減薄管道在內壓p、軸向力F和彎矩聯合作用下的極限彎矩時，由內壓p產生的環向應力σθd、σθ0和軸向力F必須同時滿足式（19）。又設管道橫截面彎曲的塑性中性軸夾角為ψ，考慮塑性中性軸位置，可按圖2所示的4種工況計算管道的極限彎矩。其中工況1的β＜ψ1，減薄區全部在彎曲壓縮區；工況2的β＞ψ2，減薄區部分在彎曲壓縮區，部分在彎曲拉伸區；工況3的β＜ψ3，減薄區全部在彎曲拉伸區；工況4的β＞ψ4，減薄區部分在彎曲拉伸區，部分在彎曲壓縮區。在工況1和工況2中，塑性中性軸下方為彎曲壓縮區；在工況3和工況4中，塑性中性軸下方為彎曲拉伸區。

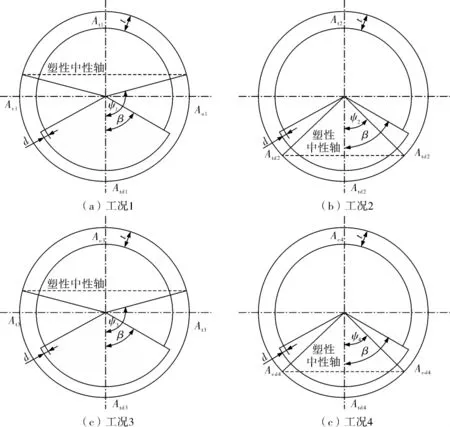
圖2 含等深減薄管道4種極限彎矩計算工況

工況1下等深減薄管道橫截面理想應力分布見圖 3。

當管道在內壓p和軸向力F作用下，再逐步施加彎矩載荷，使該管道橫截面每一處的應力（σz，σθ）逐步達到屈服條件（式（1））。 根據基本假定，釆用理想彈塑性應力-應變本構關系，且不考慮應變強化作用，彎曲載荷使管道橫截面在彎曲的塑性中性軸兩側逐步達到屈服極限狀態，最后使橫截面達到全塑性狀態。又由于工況1的管道減薄區全部在彎曲壓縮側，因此塑性中性軸在截面未減薄區，且工況1中的塑性中性軸和截面減薄段兩端點的連線將該橫截面劃分為3個極限屈服應力區，即圖3中的Ⅰ區、Ⅱ區和Ⅲ區。等深減薄管道在4種工況中的參量見表1。

表1 等深減薄管道在4種工況中的參量

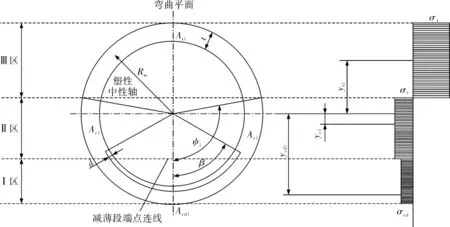
圖3 工況1下等深減薄管道橫截面理想應力分布

在工況1下，軸向力F可近似表示為：

Acd1、Ac1和At1分別為圖3中Ⅰ區、Ⅱ區和Ⅲ區對應的面積，且 Acd1=2βk1Rmt、Ac1=2(ψ1-β)Rmt、At1=2(π-ψ1)Rmt，k1按下式計算：

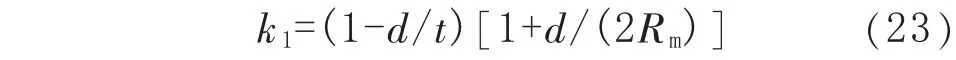
將 Acd1、Ac1和 At1的計算式代入式 （22），得到塑性中性軸夾角ψ1的計算式：

當式（24）的計算值 ψ1＞β 時，減薄管道的極限彎矩 M1（p，F）可表示為：

將 ycd1、yc1、yt1計 算 式 和 相 關 各 式 代 入 式（25），得到工況1下減薄管道的極限彎矩M1（p，F）計算式：

2.2.3 工況2計算公式

在工況2下，當管道達到全塑性狀態時，軸向力F可近似表示為：

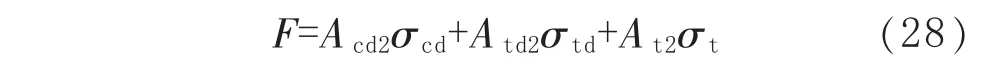
Acd2、Atd2和At2分別為對應極限屈服應力區域的面積， 且有 Acd2=2k1ψ2Rmt、Atd2=2k1(β-ψ2)×Rmt、At2=2(π- β)Rmt。將 Acd2、Atd2和 At2的計算式代入式（28），得到塑性中性軸夾角ψ2的計算式如下：

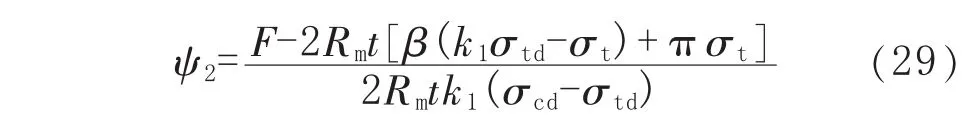
當式（29）的計算值 ψ2＜β 時，減薄管道的極限彎矩 M2（p，F）可表示為：

在工況 2下，管道的極限彎矩 M2（p，F）計算式為：

2.2.4 工況3計算公式

工況3下，塑性中性軸夾角ψ3計算式為：

管道的極限彎矩 M3（p，F）計算式為：

2.2.5 工況4計算公式

工況4下，塑性中性軸夾角ψ4計算式為：

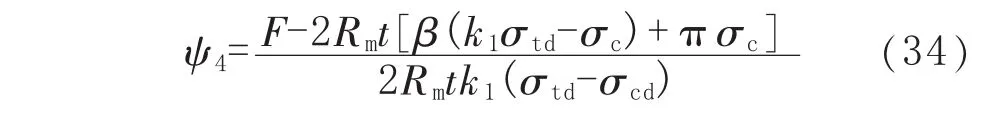
管道的極限彎矩 M4（p，F）計算式為：

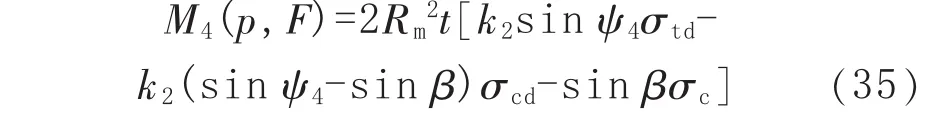
3 幾種局部減薄管道極限彎矩計算式討論

3.1 文獻[9-13]

上述建立的局部等深減薄管道極限彎矩計算新公式與文獻[9-12]中推導的計算式有很大差別。以文獻[9]為例，設σy為管材的屈服強度，Mises屈服準則為：

由Mises屈服準則導出了管道橫截面軸向壓應力極限值σcomp和軸向拉應力極限值σtenr，即為文獻[9] 中的式（3）和式（4）：

式（39）可參見文獻[9]中的式（5）。 可以看出，當 p＞0時，由式（39）確定的環向應力 σθ等于管道等深減薄區內由內壓p產生的環向應力 （式（4））。 因此由式（37）、式（38）確定的應力值 σcomp、σtenr在管道的等深減薄區滿足式 （36）的Mises屈服準則。但是管道未減薄區內由內壓p產生的環向應力（式（7））不同于式（39）計算結果。因此，用式（39）的 σθ計算的 σcomp、σtenr在管道未減薄區域就不一定滿足Mises屈服準則。這樣，文獻[9]中式（5）之后推導的管道極限彎矩計算式的理論依據就不夠充分。只有當p=0時，則σθ=0、σcomp=-σy、σtenr=σy，文獻[9]中推導的管道極限彎矩計算式才成立。

文獻[10-12]中也存在類似于文獻[9]的問題。文獻[13]第109頁最大允許彎矩Mall的計算式是采用文獻[11]的彎矩計算式，因此該計算式也值得商榷。

3.2 文獻[14-15]

文獻[14-15]釆用Hill屈服準則硏究腐蝕管道極限承載力，由式（1）得到式（2），當管道進入全塑性狀態時，管道橫截面軸向壓應力極限值σc和軸向拉應力極限值σt為：

為了計算方便，也可以表示為：

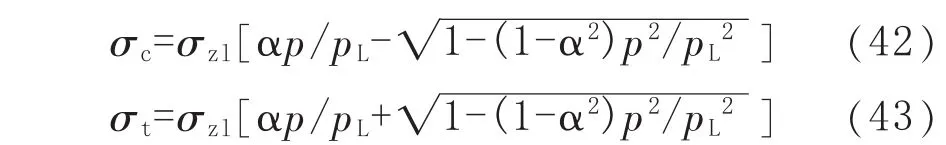
式中，pL為無缺陷管道的極限內壓，并且有pL=σθlt/Rm。

文獻 [14-15] 中對式 （40） 和式 （41）取σθ=pRm/t，又計及 pL=σθlt/Rm，就得到了式（42）和式（43），即文獻[14-15]中的計算式（5）和式（6）。因此，式（42）和式（43）在管道未腐蝕區域滿足Hill屈服準則。但在腐蝕區域內，其剩余壁厚tθ＜t，因此管壁tθ處由內壓 p產生的環向應力 σθ一般都有 σθ＞pRm/t，式（42）和式（43）計算的 σc、σt在腐蝕區就不一定滿足Hill屈服準則。這樣文獻[14-15]中式（5）和式（6）之后推導的管道極限彎矩計算式的理論依據就不充分。只有當p=0時，則 σθ=0、σc=-σzl、σt=σzl，文獻[14-15]中推導的管道極限彎矩計算式才成立。

4 不同方法計算管道極限彎矩案例分析

4.1 計算案例

設管道的平均半徑Rm=500 mm，管壁厚t=20 mm。管道鋼管軸向和環向極限應力σzl=σθl=500 MPa，各向異性系數α=0.5。設管道橫截面內壁等深減薄深度 d=10 mm，環向減薄夾角 2β=π（圖 1），其軸向長度很長。減薄區位于管道彎曲壓縮側。

該管道承受載荷為內壓p和軸向力F（F值中已包括內壓p產生的軸向力），其載荷1的p=10 MPa、F=23 000 kN， 載 荷 2 的 p=10 MPa、F=500 kN，載荷 3 的 p=7 MPa、F=-10 000 kN。采用3種方法計算管道在載荷1下的極限彎矩。

4.2 計算方法

4.2.1 本文方法

在管道減薄部位，應用式 （4）得到由內壓p=10 MPa產生的環向應力 σθd=505 MPa，由式（5）和式 （6）得到管道減薄區的軸向應力極限值σcd=10.15 MPa、σtd=494.85 MPa。

在管道未減薄部位，應用式 （7）得到內壓p=10 MPa產生的環向應力 σθ0=250 MPa，由式（8）和式 （9）得到管道減薄區的軸向應力極限值σc=-325.69 MPa、σt=575.69 MPa。

由式（16）和式（18）得 Fl=23 640.5 kN。 因此，F=23 000 kN、σθd=505 MPa 和 σθ0=250 MPa 滿足管道承載彎矩的條件，即式（19）。

由式（23）和式（27）得 k1=0.505、k2=0.510，由式（29）得塑性中性軸夾角 ψ=0.599 9＜β，最后由工況2的式 （31）計算得到管道在載荷1下的極限彎矩為4 628.6 kN·m。

4.2.2 文獻[9]方法

用文獻[9]中式（5）計算得到 σθd=505 MPa，用文獻[9]中式（29）算得 k3=0.505、ψ=0.080 9＜β。再由文獻[9]工況2中的式（28）計算得到管道在載荷1下的極限彎矩為2 624.6 kN·m。

4.2.3 文獻[15]方法

文獻[15]中表1工況2的計算公式為：

將 k1=0.505、k2=0.510、σc=-325.69 MPa、σt=575.69 MPa帶入上述公式得到ψ=0.463 3＜β，管道在載荷1下的極限彎矩為4 875.9 kN·m。

4.3 結果分析

同理，采用3種方法計算案例管道在載荷2、載荷3下的極限彎矩，結果見表2。

表2 3種方法計算的案例管道極限彎矩值

分析比較表2中的管道極限彎矩數值可知，①在p＞0的每一種載荷下，文獻[9]方法得到的計算值均最小，文獻[15]方法得到的計算值均最大，本文方法得到的計算值居中。且文獻[9]和文獻[15]方法得到的極限彎矩計算值相差都很大。②對比文獻[15]方法和本文方法計算的管道極限彎矩值，在載荷1下比較接近，而在載荷2、載荷3下相差很大。文獻[9]方法計算的極限彎矩值比本文方法得到的計算值都小得多。③當p＞0時，用文獻[9]方法計算的管道極限彎矩值一般偏保守，甚至出現異常結果。用文獻[15]方法計算的管道極限彎矩值可能很不安全。

5 結語

對在內壓p、軸向力F和彎矩M聯合作用下的局部減薄管道，存在極限彎矩的條件是，由內壓p產生的環向應力σθd、σθ0和軸向力F同時滿足式（19）。應用屈服準則和理想彈塑性本構模型，分4種工況建立了內壓、軸向力和彎矩聯合作用下局部等深減薄管道極限彎矩計算的新公式。筆者認為，文獻[9-12]中定義的環向應力在管道未減薄區不一定滿足屈服準則，文獻[14-15]釆用的環向應力σθ=pRm/t在管道腐蝕區不一定滿足屈服準則。因此，文獻[9-15]中所推導的極限彎矩計算式的理論依據不充分。