彎-剪-扭復(fù)合作用下考慮扭轉(zhuǎn)翹曲的U形薄壁混凝土梁設(shè)計方法*

許見超 郭全全 陳圣剛 刁 波 班新林

(1. 中國鐵道科學(xué)研究院集團有限公司鐵道建筑研究所， 100081， 北京； 2. 北京航空航天大學(xué)交通科學(xué)與工程學(xué)院， 100083， 北京； 3. 濟南大學(xué)土木建筑學(xué)院， 250022， 濟南∥第一作者， 助理研究員)

U形薄壁混凝土梁可大幅降低建筑物的高度，并具有隔聲效果良好、造型美觀等優(yōu)點，在城市軌道交通工程中得到廣泛應(yīng)用[1]。在列車荷載橫向偏心力、搖擺力、離心力以及橫向風(fēng)力的作用下，U形梁會受到附加扭矩的影響。U形梁為典型薄壁開口構(gòu)件，在扭矩作用下會發(fā)生約束扭轉(zhuǎn)(同時發(fā)生圣維南扭轉(zhuǎn)和翹曲扭轉(zhuǎn)，故又稱復(fù)合扭轉(zhuǎn))[2]，此時截面上不僅存在引起扭轉(zhuǎn)剪應(yīng)力的圣維南扭矩Tc和翹曲扭矩Tω，還存在引起翹曲正應(yīng)力σω的翹曲彎矩Mω。

GB 50010—2010《混凝土結(jié)構(gòu)設(shè)計規(guī)范》和JTG 3362—2018《公路鋼筋混凝土及預(yù)應(yīng)力混凝土橋涵設(shè)計規(guī)范》基于變角空間桁架模型給出了矩形截面、箱型截面和T型截面等閉口截面混凝土構(gòu)件的圣維南扭轉(zhuǎn)承載力計算公式，但這些公式并未涉及開口截面的計算。GB/T 51234—2017《城市軌道交通橋梁設(shè)計規(guī)范》給出了U形梁的圣維南扭轉(zhuǎn)承載力計算方法，但未涉及U形梁的扭轉(zhuǎn)翹曲效應(yīng)。TB 10092—2017《鐵路橋涵混凝土結(jié)構(gòu)設(shè)計規(guī)范》對此無相關(guān)規(guī)定。綜上，現(xiàn)行的混凝土橋涵設(shè)計規(guī)范針對圣維南扭轉(zhuǎn)給出了構(gòu)件設(shè)計方法，但并未包含考慮扭轉(zhuǎn)翹曲的U形薄壁混凝土梁的扭轉(zhuǎn)設(shè)計。

本文基于U形薄壁混凝土梁在彎-剪-扭復(fù)合作用下的力學(xué)性能研究成果，提出U形薄壁混凝土梁計算Mω和Tω的等效方法，進而提出彎-剪-扭復(fù)合作用下U形薄壁混凝土梁考慮扭轉(zhuǎn)翹曲效應(yīng)的設(shè)計方法。

1 U形薄壁混凝土梁的力學(xué)性能

1.1 U形薄壁混凝土梁的約束扭轉(zhuǎn)內(nèi)力和應(yīng)力

根據(jù)Vlasov薄壁開口構(gòu)件約束扭轉(zhuǎn)彈性理論(以下簡稱“Vlasov理論”)，梁端固支或簡支的U形梁的約束扭轉(zhuǎn)內(nèi)力如圖1所示。梁截面上的內(nèi)扭矩Tin等于Tc和Tω之和，梁端固支和簡支時Tc分別在1/4跨度處和支座截面處取得最大值。同時截面上還存在Mω，梁端固支時Mω在跨中和支座截面達到最大值(符號相反)，梁端簡支時Mω在跨中達到最大值。

a) 固支梁

梁端固支時的翹曲彎矩最大值Mω1、梁端簡支時的翹曲彎矩最大值Mω2的計算式分別為：

Mω1=0.5Tk[cosh(0.5L/k)-1]/

sinh(0.5L/k)

(1)

Mω2=0.5Tksinh(0.5L/k)/cosh(0.5L/k)

(2)

式中：

k——約束扭轉(zhuǎn)特征長度。

約束扭轉(zhuǎn)應(yīng)力分布如圖2所示。圣維南扭轉(zhuǎn)剪應(yīng)力τc沿U形截面環(huán)向流動，翹曲扭矩剪應(yīng)力τω在兩腹板與Tω同向，在底板部分區(qū)段與Tω反向；翹曲正應(yīng)力σω沿U形截面反對稱分布。

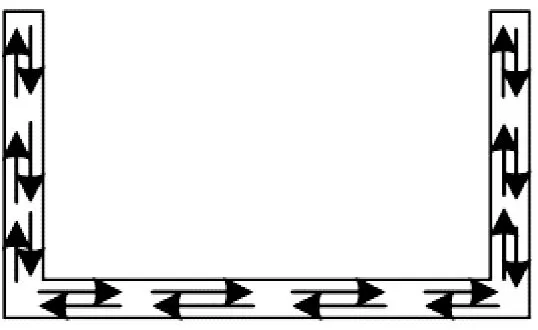
a) τc

1.2 試驗研究

本文選取5根1∶4縮尺U形薄壁混凝土梁，編號分別為試件1#、試件2#、試件3#、試件4#、試件5#。梁試件平面圖見圖3 a)，其1-1截面的配筋情況見圖3 b)。其中,試件1#～試件4#的縱筋直徑為8 mm，試件5#的縱筋直徑為10 mm。所有試件的混凝土等級均為C40。

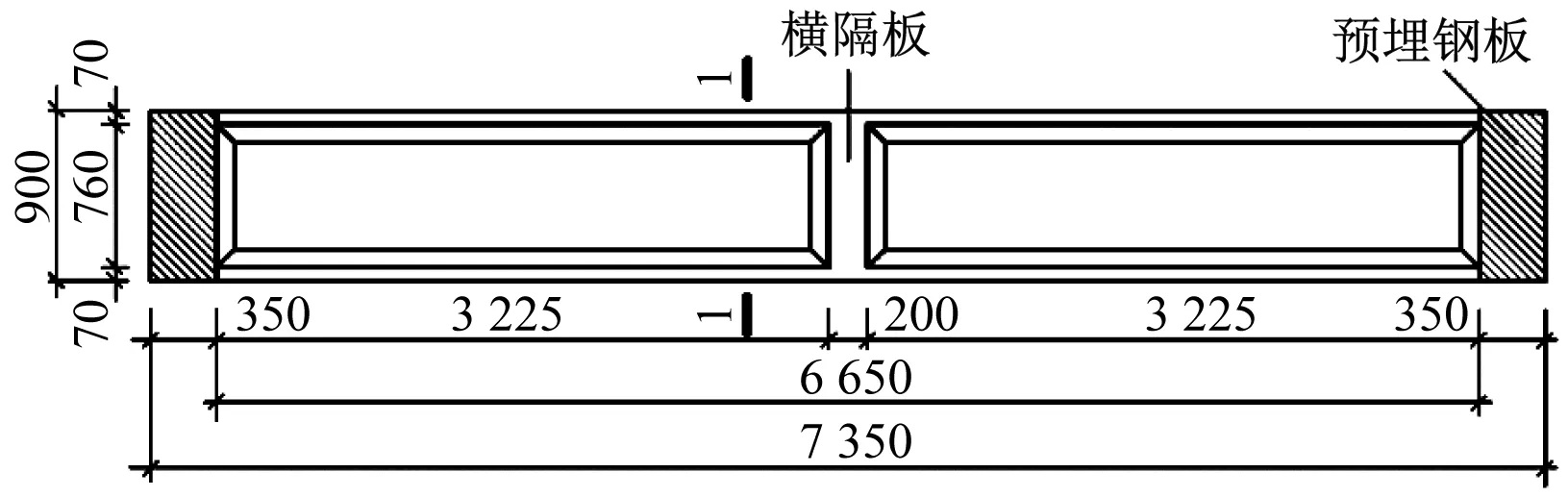
a) 梁試件平面圖

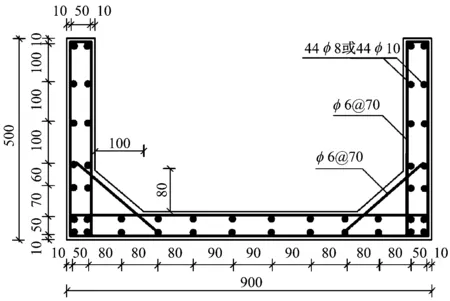
b) 1-1截面配筋

分別對這5個試件進行純扭試驗和彎-剪-扭復(fù)合加載試驗[3-5]。梁試件端部固支，通過2個千斤頂在跨中施加等大反向力實現(xiàn)扭矩加載，通過跨中荷載橫向偏心實現(xiàn)彎-剪-扭復(fù)合加載。試件在跨中處的T與Mb(彎矩)之比(以下簡稱“扭彎比”)分別為1∶5、1∶1和1∶0(即純扭試件)。試件在不同扭彎比下的極限荷載如表1所示。

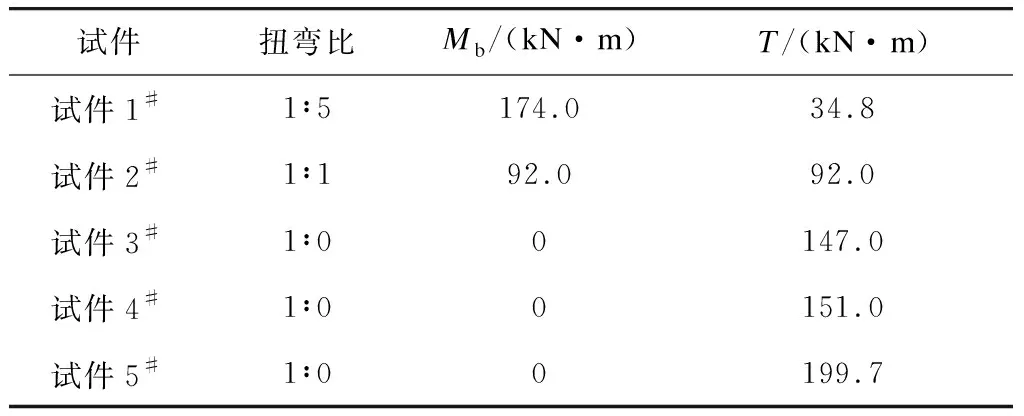
表1 U形梁試件的極限荷載

試驗結(jié)果表明，不同扭彎比作用下的U形薄壁混凝土梁試件均發(fā)生了適筋彎曲破壞。當(dāng)扭彎比為1∶5時，彎曲破壞由Mb主導(dǎo)，兩腹板同向彎曲，彎曲應(yīng)力σb和較小的σω在加載側(cè)(距荷載較近)腹板處疊加，致使加載側(cè)腹板跨中截面發(fā)生底部受拉、頂部受壓的適筋彎曲破壞。當(dāng)扭彎比為1∶1時，彎曲破壞由Mb和Mω共同主導(dǎo)，Mb和Mω產(chǎn)生的正應(yīng)力大小相當(dāng)，二者在加載側(cè)腹板處疊加產(chǎn)生彎曲破壞，在非加載(距荷載較遠)側(cè)腹板處則相互抵消、處于低應(yīng)力狀態(tài)。當(dāng)扭彎比為1∶0時，破壞由Mω主導(dǎo)，兩腹板反向彎曲，此時跨中和支座截面處的Mω大小相等，跨中截面和支座截面均發(fā)生彎曲破壞。

1.3 數(shù)值模擬分析

基于試驗研究結(jié)果[6-7]，本文利用有限元數(shù)值模型，選取了邊界條件、跨高比以及縱筋-箍筋配筋強度比3個關(guān)鍵參數(shù)，對U形薄壁混凝土梁的受力性能進行系統(tǒng)研究，取得以下主要結(jié)論：

1) 純扭矩作用下，在跨高比逐漸增加的過程中，梁端固支U形梁的破壞模式由Tω主導(dǎo)的剪切型破壞(跨高比為8～10時)演變?yōu)橛蒑ω主導(dǎo)的彎曲破壞(跨高比為12～16時)，再演變?yōu)閺澢?剪切破壞(跨高比為18～20時Mω主導(dǎo)的彎曲破壞和Tc主導(dǎo)的剪切型破壞同時發(fā)生)。當(dāng)梁端簡支時，隨著跨高比變化，上述破壞過程的演變速度更快。

2) 在彎-剪-扭復(fù)合作用下，隨著扭彎比的增加，U形梁破壞模式的變化趨勢為由彎曲破壞向剪切型破壞轉(zhuǎn)變。在已有工程應(yīng)用中，連續(xù)U形梁的跨高比一般為13～15，此時任意扭彎比作用下均會發(fā)生彎曲破壞；簡支U形梁的跨高比一般為10～12，此時扭彎比小于1∶2時會發(fā)生彎曲破壞，扭彎比大于1∶2時會發(fā)生彎曲-剪切破壞。

1.4 極限狀態(tài)內(nèi)力分析和承載力計算

基于彎-剪-扭復(fù)合作用下U形薄壁混凝土梁的試驗研究和有限元參數(shù)分析結(jié)果，本文進一步進行極限狀態(tài)內(nèi)力分析和承載力計算，設(shè)V為截面剪力。如圖4 a)所示，將半U截面上的σω積分為等效彎矩Meq和軸力Neq，即將Mω等效為作用在半U截面上的Meq和Neq；如圖4 b)所示，將Tω等效為作用在兩腹板上的剪力Vω。在彎-剪-扭復(fù)合作用下，彎曲破壞發(fā)生在Mb和Mω取最大值跨度位置的加載側(cè)半U截面處，其相應(yīng)的內(nèi)力為Neq、合成彎矩(Meq+Mb/2)以及合成剪力(V/2+Vω)。剪切型破壞發(fā)生在Tc取最大值跨度位置的加載側(cè)腹板處，其相應(yīng)的內(nèi)力為(Wtw/Wt)Tc(Wtw為腹板受扭塑性抵抗矩，Wt為U形截面受扭塑性抵抗矩)，以及合成剪力(V/2+Vω)。

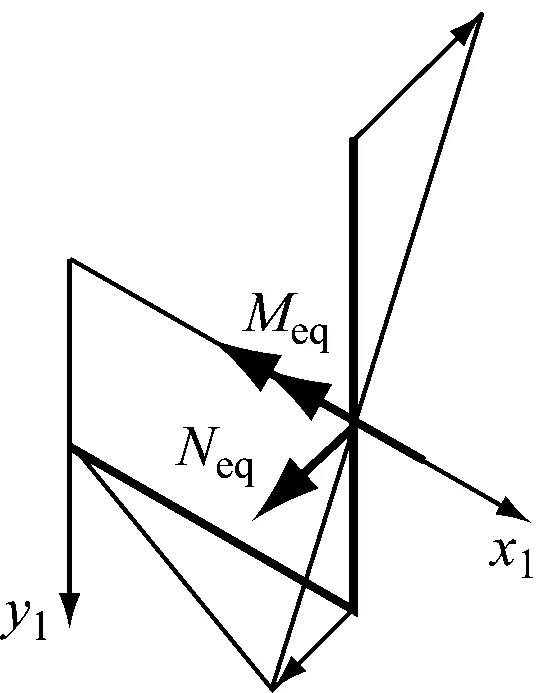
a) 等效彎矩和軸力

考慮到U形梁腹板上分布縱筋較多，加載側(cè)半U截面的正截面軸力-彎矩承載力計算可根據(jù)剪力墻正截面承載力計算方法進行，具體可見文獻[3]。加載側(cè)腹板的抗剪和扭-剪承載力根據(jù)變角空間塑性桁架理論進行計算。對于任意特定扭彎比加載工況，其截面內(nèi)力扭矩-彎矩-剪力比例一定，分別在彎曲破壞危險截面處和剪切型破壞危險截面處令截面內(nèi)力等于截面承載力，可計算得到發(fā)生彎曲破壞和剪切型破壞的外荷載Pf和Ps，這2種破壞外荷載的較小值即為真實極限荷載計算值，相應(yīng)的破壞模式為真實破壞模式。經(jīng)與試驗及數(shù)值模擬分析結(jié)果對比，三者相互吻合良好。

2 U形薄壁混凝土梁設(shè)計方法

2.1 內(nèi)力分析

內(nèi)力分析的關(guān)鍵為約束扭轉(zhuǎn)內(nèi)力分析，采用上文所述的內(nèi)力等效方法。具體步驟為根據(jù)U形梁支撐條件和外荷載分布，采用Vlasov理論進行約束扭轉(zhuǎn)內(nèi)力計算，再將Mω在彎曲破壞危險加載側(cè)半U截面上等效為彎矩Meq和軸力Neq，在剪切破壞危險加載側(cè)腹板上將Tω等效為剪力Vω。疊加截面上的彎矩和剪力后即得設(shè)計內(nèi)力。

2.2 承載力設(shè)計

基于內(nèi)力分析結(jié)果進行承載力設(shè)計，對于加載側(cè)半U截面，其正截面承載力計算采用上文1.4節(jié)的計算方法。對于加載側(cè)腹板的抗剪和扭-剪承載力計算，采用現(xiàn)行《城市軌道交通橋梁設(shè)計規(guī)范》方法。

相比現(xiàn)行規(guī)范，本文設(shè)計方法的關(guān)鍵點在于采用U形薄壁梁的約束扭轉(zhuǎn)內(nèi)力并進行等效，而不是忽略U形薄壁梁的翹曲扭轉(zhuǎn)效應(yīng)。

3 是否考慮扭轉(zhuǎn)翹曲的設(shè)計內(nèi)力和極限荷載計算值差異分析

3.1 設(shè)計內(nèi)力對比

本文以在試驗梁試件跨中作用1 kN·m的外扭矩為例進行分析。跨中加載側(cè)半U截面以及1/4跨度處加載側(cè)腹板的設(shè)計內(nèi)力如表2～3所示。由表2～3可以看出，是否考慮扭轉(zhuǎn)翹曲所得到的設(shè)計內(nèi)力在內(nèi)力類別和數(shù)值上均有差異顯著。

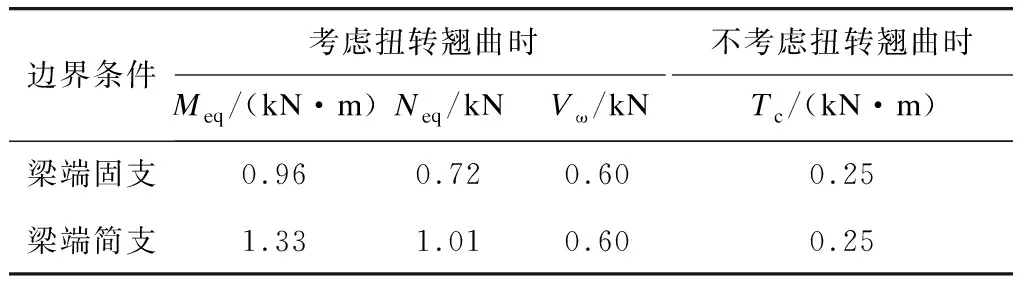
表2 U形梁加載側(cè)半U截面的設(shè)計內(nèi)力計算結(jié)果

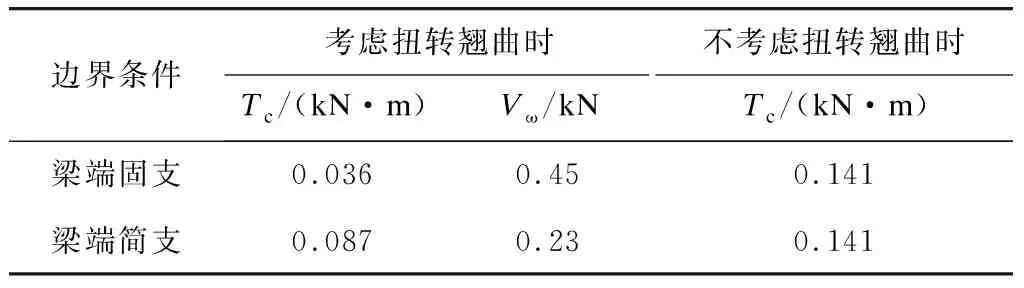
表3 U形梁加載側(cè)腹板的設(shè)計內(nèi)力計算結(jié)果

3.2 極限荷載計算值對比

以試件2#的幾何、材料和邊界參數(shù)為例，分別計算考慮扭轉(zhuǎn)翹曲、忽略扭轉(zhuǎn)翹曲2種情況下試件的極限荷載。如圖5所示，V與Mb的關(guān)系為：Mb=VL/4。從圖5可知，當(dāng)扭彎比較小(約小于1∶8)時，忽略扭轉(zhuǎn)翹曲的極限荷載計算值偏高，即偏于危險；當(dāng)扭彎比較大(約大于1∶8)時，忽略扭轉(zhuǎn)翹曲的極限荷載計算值偏小；純扭轉(zhuǎn)(扭彎比為1∶0)時，考慮扭轉(zhuǎn)翹曲的極限扭矩計算值為133.4 kN·m，而忽略翹曲的極限扭矩計算值為53.4 kN·m，二者差異巨大。

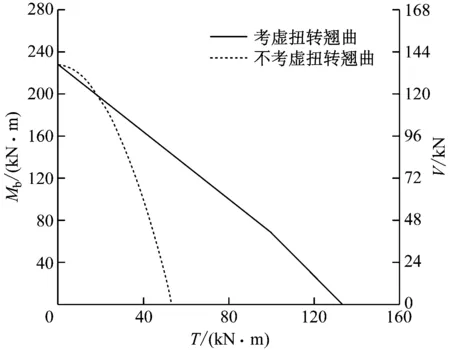
圖5 U形梁極限荷載的計算結(jié)果

4 結(jié)論

1) 扭轉(zhuǎn)翹曲所得到的設(shè)計內(nèi)力結(jié)果在內(nèi)力類別和數(shù)值上均差異顯著，U形薄壁混凝土梁的設(shè)計應(yīng)考慮扭轉(zhuǎn)翹曲的影響。

2) 當(dāng)扭彎比較小(約小于1∶8)時，忽略扭轉(zhuǎn)翹曲時得到的極限荷載計算值偏大；當(dāng)扭彎比較大(約大于1∶8)時，不考慮扭轉(zhuǎn)翹曲時得到的極限荷載計算值偏小。