超臨界二氧化碳渦輪機主軸靜壓軸承承載特性分析

鄭培培，李倫，李濟順，許世鈺

(河南科技大學 a.機電工程學院；b.河南省機械設計及傳動系統重點實驗室，河南 洛陽 471003)

0 引言

超臨界二氧化碳(Supercritical Carbon Dioxide，S-CO2)循環是極具發展潛力的新一代發電循環技術。超臨界狀態下的CO2相較于水蒸氣具有更高的能量密度和極低的內摩擦功耗，可極大地提高熱循環效率，減小發電裝置及配套系統的體積[1-2]。此外，區別于傳統水蒸氣循環需要消耗大量的水，S-CO2循環屬于完全密閉循環，無需額外的氣體補給。因此，S-CO2循環發電技術特別適合于太陽能資源充足且干旱缺水的地區，如澳大利亞、非洲及我國西部地區。S-CO2循環發電技術是未來人類能源開發利用的主要研究方向之一。

渦輪機作為S-CO2動力循環的核心部件，其主軸運轉的穩定性極其重要，因此對渦輪機主軸的支承軸承提出了更苛刻的要求。目前，氣體靜壓軸承因其運轉精度高，無污染，摩擦小，在醫療設備和高精密機床上應用較為廣泛[3-4]。國內外學者針對氣體靜壓軸承進行了廣泛而深入的研究，目前針對壓力和承載力計算主要有以下3種方法：

1)簡化的工程計算方法。如文獻[5]開發了一種簡單的設計方法，以協助軸承的設計或選擇，并研究分析了進氣孔直徑、進氣壓力、軸承內徑對承載力和剛度的影響。文獻[6-7]根據空氣軸承的特點，結合潤滑氣體特性，分析了氣體靜壓軸承承載力和剛度等特性。

2)利用有限差分法對靜壓軸承氣膜的雷諾方程進行差分，借助于計算機進行求解。文獻[8]將軸承氣膜流動簡化為量綱一的Navier-Stokes方程，利用牛頓法對其離散并求解，所建立的解析模型為分析高精度旋轉氣體軸承的動靜態性能提供了一種有價值的手段。文獻[9]在雷諾方程中增加了流量項，將不同坐標系內的雷諾方程變換成為相同形式，簡化了數值計算，并對微分方程離散方法加權余量法、變分求極值法進行了分析討論。

3)利用有限元方法，構建流體域的三維模型，通過流體分析工具進行仿真計算。文獻[10]研究了高速主軸空氣靜壓滑動軸承在不同工況下的剛度特性，針對不同長徑比、供氣孔直徑、供氣壓力進行了對比分析，結果表明幾何結構對剛度有顯著的影響。文獻[11]采用數值分析法對空氣靜壓軸承氣膜壓力分布進行了分析，并推算出軸承的承載能力和靜剛度的計算公式，為空氣軸承板形儀的結構設計和性能分析提供一定的理論依據。文獻[12]研究了空氣靜壓軸承的動剛度和阻尼系數，結果表明由于氣體的可壓縮性，氣體靜壓軸承的動態特性表現出非線性特性，這種非線性特性在超薄氣膜間隙和大供氣壓力條件下尤為顯著。文獻[13]建立了小孔節流空氣靜壓軸承雙向流固耦合數值模擬模型，采用數值模擬法獲取了設計參數對承載力和剛度的影響規律，并在氣體靜壓試驗平臺上對自行研制的空氣靜壓軸承進行靜動態特性測試試驗驗證。文獻[14]利用有限體積法分析了靜壓軸承旋轉狀態下軸承承載力和耗氣量的變化規律，結果表明轉速增加引起較為明顯的動壓效應，動壓效應使軸承承載力明顯提高。文獻[15]結合仿真方法和正交試驗方法分析了軸承參數對承載能力的影響，揭示了各個參數對承載力影響的主次順序。

上述研究方法和文獻所涉及的靜壓軸承均以空氣為潤滑介質，而對S-CO2為潤滑介質的靜壓軸承承載力和剛度的研究還比較少。此外，由于S-CO2的物理性質與空氣差別較大，這給S-CO2作為潤滑介質的靜壓軸承承載力和剛度的研究帶來一定的難度。因此，現以S-CO2渦輪機主軸支承靜壓軸承為研究對象，對比分析了不同參數對S-CO2潤滑軸承承載特性的影響。

1 主軸靜壓軸承結構及工作原理

1.1 支承靜壓軸承結構

S-CO2渦輪機的汽輪處于懸伸狀態，且S-CO2的工作溫度為550～750 ℃。本文選用的主軸支承靜壓軸承可以提高主軸的運轉穩定性和剛度，并能夠利用低溫下的S-CO2完成對主軸的冷卻。靜壓軸承有多種形式，本文選取小孔節流形式的靜壓軸承(圖1)，圓周節流孔數目為8個且呈均勻分布(圖1b)。節流孔軸向排數對支承也有一定的影響，因此選取單、雙排節流孔靜壓軸承進行對比分析，所選用軸承的參數見表1。

圖1 渦輪機徑向氣體軸承結構Fig.1 Structure of radial gas bearing for turbine

表1 渦輪機徑向氣體軸承結構參數Tab.1 Structure parameters of radial gas bearing for turbine

1.2 支承靜壓軸承工作原理

氣體支承軸承依靠外部的供氣裝置在氣膜間隙內形成高壓氣體膜以滿足主軸的運轉需要，高壓氣體通過圓周分布的節流孔進入軸承間隙。在空載情況下，軸承四周氣膜間隙一致，壓力處處相等，形成的承載力相互平衡。在y方向載荷作用下，主軸在y方向將形成偏心，導致y軸上半部分氣膜間隙增大，壓力減小，下半部分氣膜間隙減小，壓力增大，上下兩部分的壓力差使主軸再次達到平衡。

1.3 支承靜壓軸承承載力和剛度理論

靜壓軸承的流體域內部流動為穩態流動，根據連續性方程，每個節流孔質量流量為

(1)

βi=pdi/pa,

式中：A為節流孔面積；p0為進氣口壓力；φ為流量系數；ρ為流體密度;k為氣體常數;pdi為出氣口壓力;pa為環境壓力;i為第i個節流孔，其與基準線的夾角為αi。

不考慮其徑向y和圓周方向z的流動速度，其內部流體的運動方程為

(2)

式中:p為壓力；μ為黏性系數；u為流體軸向流動速度。對其流體域氣體流動，有y=0，u=0和y=h，u=0,對(2)式積分可得流體域氣體在軸向的速度分布

(3)

式中:y為徑向尺寸；h為對應的氣膜厚度。

由(1),(3)式可知

(4)

(5)

式中：b為第i等份氣膜在圓周方向尺寸；ρa為靜壓軸承出口流體密度。進一步，流體域軸向在z點的壓力可表示為

(6)

針對單個節流進氣孔,其形成的壓力合力為

Fi=2pdi(L-2l)Rsin(π/n)+

(7)

對(7)式沿圓周方向積分可得整體氣膜承載力為

(8)

由(6)式可進一步求得膜承載力為

(9)

σ=pa/p0。

根據剛度定義，剛度K為

(10)

式中：Δe為相鄰偏心點的偏心增量；W(e+Δe)和W(e)為該2點的承載能力。

2 CFD仿真預處理

2.1 模型建立及網格劃分

利用CFD方法分析研究主軸支承靜壓軸承的特性，主要分析軸承氣膜壓力、承載力和剛度等特性的影響因素及其變化規律。根據靜壓軸承的結構參數，在ANSYS Workbench平臺上，Design Modeler模塊中建立靜壓軸承的流體域三維模型，如圖2a所示。氣膜網格劃分是數值計算預處理極其重要的環節，網格質量不僅關系到數值計算的效率，也直接關系到計算的精度和準確性。由于靜壓軸承的氣膜間隙遠小于軸承的內徑和寬度，因此網格劃分在氣膜間隙位置需要更加的精細。在Workbench meshing模塊中對流體域進行網格劃分(圖2b)，并對進氣孔位置網格進行了加密，以滿足速度和壓力在此處的急劇變化。

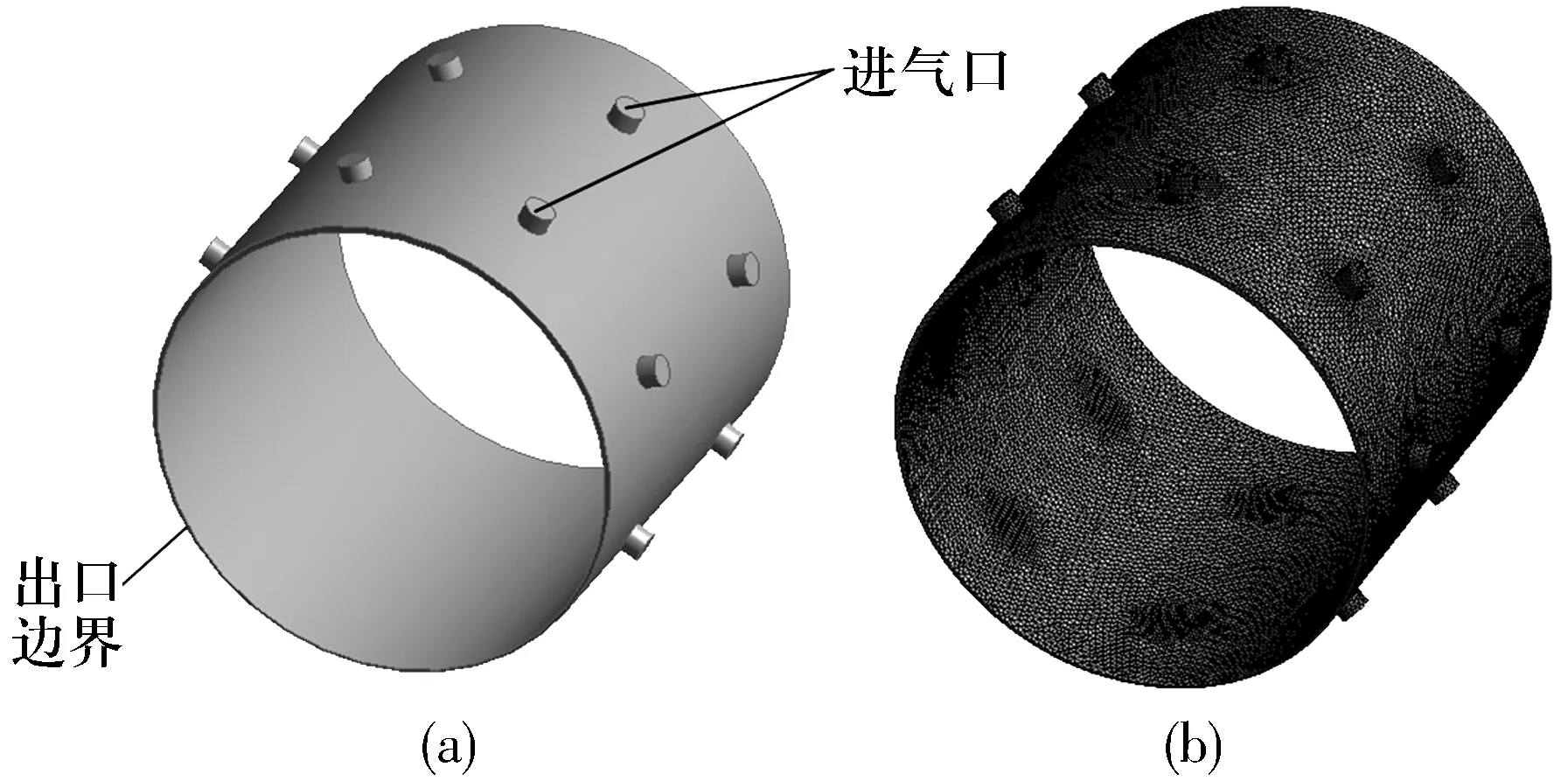
圖2 靜壓軸承整體氣膜及流體域網格Fig.2 Integral air film and fluid domain grid of hydrostatic bearing

2.2 S-CO2物性特點

S-CO2與普通CO2相比有更加復雜多變的物性，物性隨溫度和壓力的改變表現出明顯的差異性。8 MPa壓力下S-CO2的物性隨溫度的變化曲線如圖3所示，由圖可知：比熱容在臨界點附近出現峰值，且臨界點前后比熱容數值變化較小；密度和導熱系數在臨界點出現突變，物性數值呈現大幅度減小。黏度是S-CO2重要的物性參數，直接影響到渦輪機主軸的摩擦功耗，因S-CO2兼有氣體和液體的雙重性質，其黏度接近于普通氣體而小于液體，在給定超臨界壓力下，其黏度在臨界點急劇減小，呈現陡直下降特點；隨溫度的繼續升高，在超臨界狀態其黏度變化較小，8 MPa壓力下保持在4.5×10-5Pa·s，與普通狀態下CO2的黏度相比減小一半。

圖3 8 MPa壓力下S-CO2的物性曲線Fig.3 S-CO2 physical property curve under pressure of 8 MPa

復雜多變的物性易導致靜壓軸承流體域內仿真結果出現不收斂，因此對S-CO2物性的定義十分重要。本文采用美國國家標準數據庫(National Institute of Standards and Technology,NIST)S-CO2氣體物性的數據，通過軟件對其物性進行擬合，利用Fluent內置函數對物性進行定義。

2.3 數值計算邊界條件及仿真工況

因S-CO2氣體物性的特殊性，流體在軸承間隙內的流動是十分復雜的三維流動。利用流體分析工具Fluent可對靜壓軸承內部流體進行相對準確的分析，在數值計算前需做出以下假設：1)氣體在氣膜間隙方向不流動，即無速度變化；2)忽略慣性力和黏性力；3)忽略主軸表面粗糙度對氣膜的影響。

仿真計算湍流模型要根據實際工況選擇，針對本文的分析工況，渦輪機主軸的轉速為50 000 r/min，軸承內部雷諾數較高，適合選用標準k-ε模型。選擇默認的基于壓力的求解器(Pressure Based)，求解算法設置為SIMPLEC分離算法。收斂殘差決定了計算效果，默認值為10-3，本文設定為10-5。仿真壓力入口和出口如圖2a所示，其邊界條件是：壓力設定為絕對壓力，入口壓力為8 MPa，出口邊界設定為大氣壓力0.1 MPa，主軸偏心率設置為0，0.1，0.2，0.3，0.4，0.5。

3 數值計算結果分析

3.1 流體域壓力分布分析

3.1.1 軸承結構和氣膜間隙的影響

偏心率為0.5，供氣壓力為8 MPa時，不同進氣結構及氣膜間隙下的壓力云圖如圖4所示，由圖可知：無論單排還是雙排進氣結構，壓力沿軸向均呈對稱分布；當氣膜間隙一致時，雙排進氣結構較單排進氣結構的靜壓軸承流體域壓力更高，且更加均勻；在結構一定的條件下，氣膜間隙對流體域壓力變化影響較為明顯，可以看出0.3 mm的氣膜壓力高于0.5 mm。

圖4 不同進氣結構及氣膜間隙下流體域壓力分布云圖Fig.4 Pressure distribution nephograms in fluid domain under different gas supply structures and gas film clearances

3.1.2 偏心率對流場壓力的影響

采用圖1b中的坐標系，偏心方向為-y方向，進氣壓力為8 MPa，不同偏心率下的氣膜壓力分布如圖5所示。由圖5可知：在渦輪機主軸未受載情況下，主軸偏心率ε=0，流體域中節流孔出口處壓力最高，出口邊界壓力最低；因流體域內氣膜間隙一致，氣膜壓力分布在圓周方向和軸向方向呈現嚴格的對稱性(圖5a);隨著偏心率不斷增大，x軸上方氣膜間隙逐漸增大，導致該區域氣膜壓力變小；x軸下方氣膜間隙和氣膜壓力則相反，對比圖5b—圖5d可明顯看出其壓力變化;x軸上下壓力差的存在使主軸在偏心方向有更大的承載能力，且偏心率越大，壓力差越明顯，軸承的承載能力更加突出。

3.2 主軸靜壓軸承承載力特性

不同進氣結構和氣膜間隙下靜壓軸承承載力隨偏心率的變化曲線如圖6所示,在軸承進氣結構一定的條件下，承載力隨偏心率的增大而增大，且承載力和偏心率呈現非線性正相關關系。在偏心率較小時，承載力變化較大，隨偏心率繼續增大，承載力增長幅度逐漸減緩。在偏心率一定條件下，雙排進氣結構靜壓軸承承載能力比單排結構更高，且平均氣膜間隙較小的靜壓軸承承載力更高。例如平均氣膜間隙0.3 mm的雙排進氣結構靜壓軸承承載力較0.5 mm的提高10%。

圖6 不同進氣結構及氣膜間隙下承載力和偏心率的變化關系Fig.6 Variation curves of load capacity with eccentricity under different gas supply structures and gas film clearances

3.3 主軸靜壓軸承剛度特性

不同進氣結構和氣膜間隙條件下，靜壓軸承的剛度隨偏心率的變化曲線如圖7所示,在相同的偏心率下，雙排進氣結構的靜壓軸承剛度明顯高于單排進氣結構，且平均氣膜間隙較小的靜壓軸承剛度更高。因為偏心率和承載力呈非線性關系，所以剛度隨偏心率變化而變化，在偏心率增大過程中，剛度先增大后減小，極值出現在偏心率0.32附近；在偏心率較小條件下，剛度曲線變化梯度較明顯，在大偏心率下，剛度曲線下降較緩慢，且剛度的最大值位置并非承載力的最大值。

圖7 不同進氣結構及氣膜間隙下剛度隨偏心率的變化曲線Fig.7 Variation curves of stiffness with eccentricity under different gas supply structures and gas film clearances

4 結論

基于Fluent軟件對S-CO2渦輪機主軸支承靜壓軸承進行了數值分析，獲得了靜壓軸承潤滑氣膜的壓力分布云圖，揭示了S-CO2潤滑條件下的承載力和剛度隨偏心率的變化規律:

1)不存在偏心條件下，軸承氣膜圓周方向壓力均勻分布，軸承承載力為零；氣膜間隙一定時，雙排進氣結構較單排進氣結構的靜壓軸承流體域壓力更高。隨偏心率增大，氣膜間隙減小區域壓力增加，氣膜間隙增大區域壓力減小。

2)在偏心率一定時，雙排進氣結構靜壓軸承承載能力比單排結構更高，且平均氣膜間隙較小的靜壓軸承承載力更高；在偏心率不斷增大過程中，承載力和偏心率呈非線性正相關關系。

3)雙排進氣結構的靜壓軸承剛度高于單排進氣結構，且平均氣膜間隙較小的靜壓軸承剛度更高。因承載力和偏心率的非線性關系，剛度和承載力呈現出高度的非線性。剛度在隨偏心率增大過程中先增大后減小，偏心率為0.32時出現極值，且極值前的剛度增長梯度高于極值后的減小梯度。