柴油發動機連桿-軸瓦摩擦副接觸變形的數值計算

韋浩，高申德，吳玉國，梅加化，時禮平,3,4

(1.安徽工業大學 機械工程學院，安徽 馬鞍山 243032；2.安慶中船柴油機有限公司，安徽 安慶 246005；3.特種服役環境的智能裝備制造國際科技合作基地，安徽 馬鞍山 243032；4.特種重載機器人安徽省重點實驗室，安徽 馬鞍山 243032)

軸瓦連接柴油機的曲軸和活塞，構成曲柄滑塊機構，實現連桿由往復運動到旋轉運動的轉換。當活塞運動至做功行程止點時，連桿處于最大壓縮狀態，載荷達到最大，從而擠壓軸瓦[1]，并使其與曲軸易發生碰撞，甚至出現燒瓦和抱軸現象，此階段柴油機最易發生故障。

針對柴油機連桿-軸瓦摩擦副接觸變形問題，文獻[2]利用有限元軟件模擬計算出高速發動機連桿-軸瓦摩擦副在動、靜載荷下的變形，結果表明隨氣缸壓力和慣性力的方向和大小的變化，連桿內孔和軸瓦輪廓變成非圓形。文獻[3]以雷諾方程為基礎,采用積分有限元法對混合軸承進行變形計算，結果得出彈性變形和熱變形對混合軸承的承載性能有著重要的影響，且這些變形可以根據軸承聚合物層的性質調節。文獻[4]在考慮軸承變形的情況下，建立了軸承過渡速度的解析模型，并與以往的數值計算結果對比，表明新方法對過渡速度的預測具有良好的相關性。文獻[5]提出單純形優化算法，并考察了在不同螺栓預緊力和過盈量的條件下某型號柴油機主軸承孔和主軸瓦的變形，結果表明保持橫拉螺栓預緊力不變，軸承孔的變形量隨豎拉螺栓預緊力的增大呈線性遞增，軸瓦的變形隨過盈量的增加呈線性遞增。文獻[6]針對發動機裝配后連桿-軸瓦摩擦副產生異響的現象，在分析可能產生該問題原因的基礎上提出了抑制異響現象的策略為減小軸瓦半徑公差0.015 mm，壓縮曲軸半徑上偏差0.007 mm以及連桿內孔上偏差0.002 mm。

綜上所述，減小發動機連桿-軸瓦摩擦副的變形對于減少發動機故障顯然有效，而不同工況參數將促使發動機連桿-軸瓦摩擦副產生不同程度的接觸變形[7]。因此，本文利用ABAUQS有限元與正交試驗相結合的方式對大端軸瓦在最大爆發壓力下的變形量進行研究，考察螺栓預緊力、過盈量與摩擦因數對軸瓦最大接觸變形量的影響，找出最優參數組合，以期降低軸瓦碰撞的風險。

1 連桿-軸瓦有限元模型的建立

1.1 連桿軸瓦有限元模型

運用Solidworks軟件建立連桿-軸瓦的三維模型。為提高ABAQUS有限元軟件分析效率，取連桿厚度(xOz)方向上的對稱模型作為分析對象，并將簡化后的1/2模型另存為SAT格式以便導入ABAQUS有限元軟件，結果如圖1所示。

圖1 1/2連桿-軸瓦有限元模型爆炸圖Fig.1 Explosive diagram of 1/2 finite element model for connecting rod-bearing bush

1.2 連桿軸瓦參數

連桿-軸瓦的幾何參數見表1，連桿組件的材料性能參數見表2。

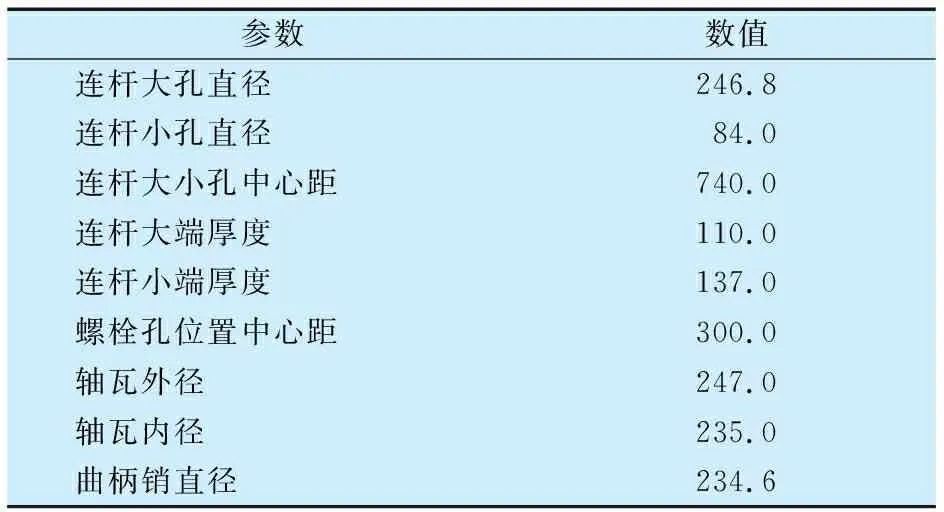
表1 連桿-軸瓦的幾何參數Tab.2 Geometric parameters of connecting rod-bearing bush mm

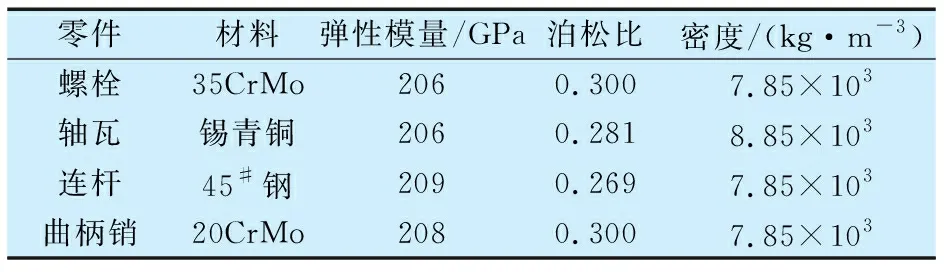
表2 連桿組件的材料性能參數Tab.2 Material performance parameters of connecting rod components

1.3 連桿軸瓦網格劃分

連桿網格劃分類型為C3D8I，單元數為71 654，節點數為952 249；軸瓦網格劃分類型為C3D8I，單元數為11 000，節點數為145 444；螺栓網格劃分類型為C3D8I，單元數為12 228，節點數為14 586；曲柄銷網格劃分類型為C3D8I，單元數為23 672，節點數為226 736；活塞銷網格劃分類型為R3D4，單元數為850，節點數為935。整個模型的網格劃分如圖2所示。

圖2 連桿-軸瓦網格劃分Fig.2 Meshing of connecting rod-bearing bush

1.4 載荷與邊界條件的設置

1.4.1 最大爆發壓力數值的確定

柴油機連桿由于氣體燃燒的作用處于最大壓縮狀態，且連桿與軸瓦是緊配合，所以氣體爆發力通過連桿傳遞至軸瓦，使軸瓦此時的變形量達到最大，最大氣體爆發壓力為

Fg=(P-P′)πD2/4，

(1)

式中：Fg為最大氣體爆發壓力；P為缸內氣體壓強，P=13.3 MPa；P′為曲軸箱壓力，一般為大氣壓力，0.1 MPa；D為氣缸直徑，D=280 mm。

1.4.2 載荷與邊界條件的設置

連桿-軸瓦xOy對稱面設置為U2=UR1=UR3=0；連桿-軸瓦yOz對稱面設置為U3=UR1=UR3=0；曲柄銷yOz對稱面設置為固定約束；活塞銷設置為U2=U3=UR1=UR2=UR3=0；其中U1,U2,U3,UR1,UR2,UR3為連桿構件的6個自由度。載荷以集中力的形式施加于活塞銷的參考點(RP)，結果如圖3所示。

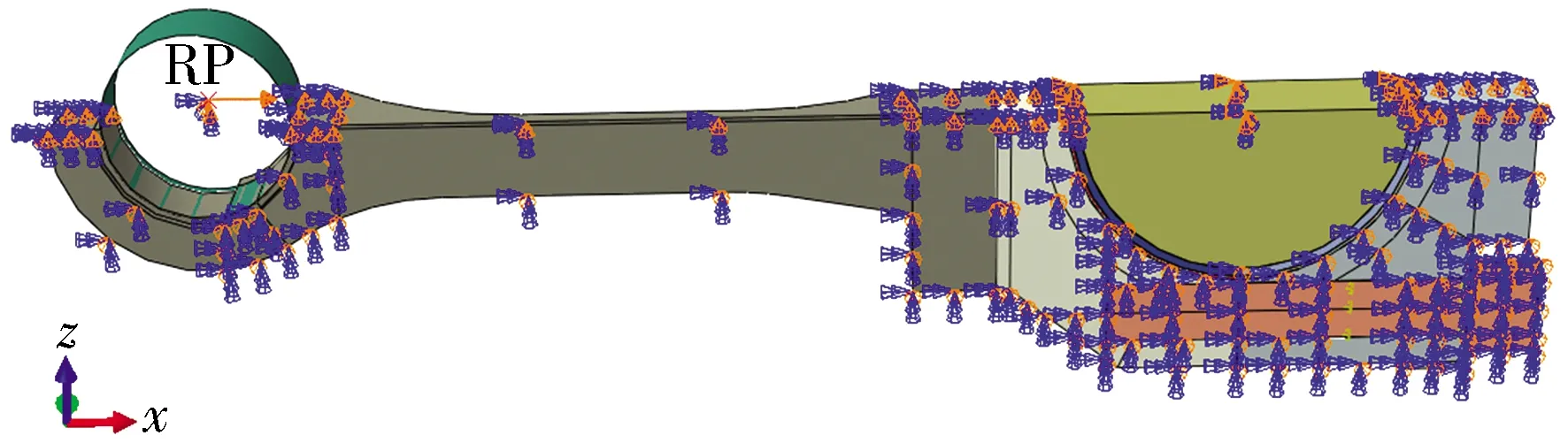
圖3 連桿-軸瓦有限元模型載荷與邊界條件的設置Fig.3 Setting of load and boundary conditions of finite element model of connecting rod-bearing bush

1.4.3 接觸對的定義

設置7個接觸對：螺帽與連桿蓋、螺栓與螺孔、桿蓋與桿身、軸瓦瓦背與連桿大頭孔、上軸瓦與下軸瓦、曲柄銷與軸瓦內表面、剛體銷與連桿小頭，各接觸對之間的接觸方式設置為小滑動接觸。由于軸瓦與連桿孔座之間的接觸面是分析重點，需設置不同的摩擦因數進行對比分析，其余接觸面之間比較光滑，摩擦因數均設置為0.25。

2 數值模擬結果與分析

2.1 單因素試驗

2.1.1 螺栓預緊力對軸瓦最大接觸變形量的影響

采用螺栓拉伸器對連桿螺栓進行預緊，最大預緊力為

Fm=PdS，

(2)

式中：Fm為螺栓承受的最大預緊力；Pd為螺栓拉伸器泵的壓強；S為液壓油缸的受力面積。由(2)式確定螺栓承受最大預緊力為680 kN。

軸瓦與連桿過盈量為0.24 mm，其接觸面之間摩擦因數為0.3，氣體爆發壓力為406 397 N的條件下，選取螺栓預緊力分別為600,640,680,700,760 kN進行數值模擬。不同螺栓預緊力下軸瓦變形量分布區域基本一致，但軸瓦最大接觸變形量不同，故取螺栓預緊力為600，760 kN時的軸瓦變形量結果，如圖4所示。

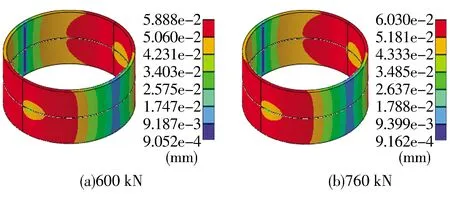
圖4 不同螺栓預緊力下軸瓦變形量分布Fig.4 Deformation distribution of bearing bush under different bolt preloads

由圖4可知:螺栓預緊力由600 kN增大到760 kN，軸瓦最大接觸變形量由5.888×10-2mm增大到6.030×10-2mm，增加了2.4%；軸瓦最大接觸變形量出現在軸瓦接觸部位周圍區域，這是由于連桿大端沿豎直中心線方向產生收縮變形，軸瓦受到擠壓隨之產生變形。

螺栓預緊力與軸瓦最大接觸變形量的關系如圖5所示，螺栓預緊力與軸瓦最大接觸變形量呈正線性關系，這是由于螺栓預緊力將桿蓋與連桿主體連接，使連桿大端孔受到擠壓產生變形，而軸瓦緊貼連桿大端孔裝配同樣受到擠壓變形，預緊力越大產生的變形越大。螺栓預緊力過大會導致連桿螺栓疲勞失效，使軸瓦與連桿接觸條件變差，發生松動；螺栓預緊力過小，軸瓦與連桿大頭孔之間接觸不良，甚至會出現間隙，導致熱傳遞效率變低。根據實際生產經驗，螺栓預緊力取640～680 kN較合適。

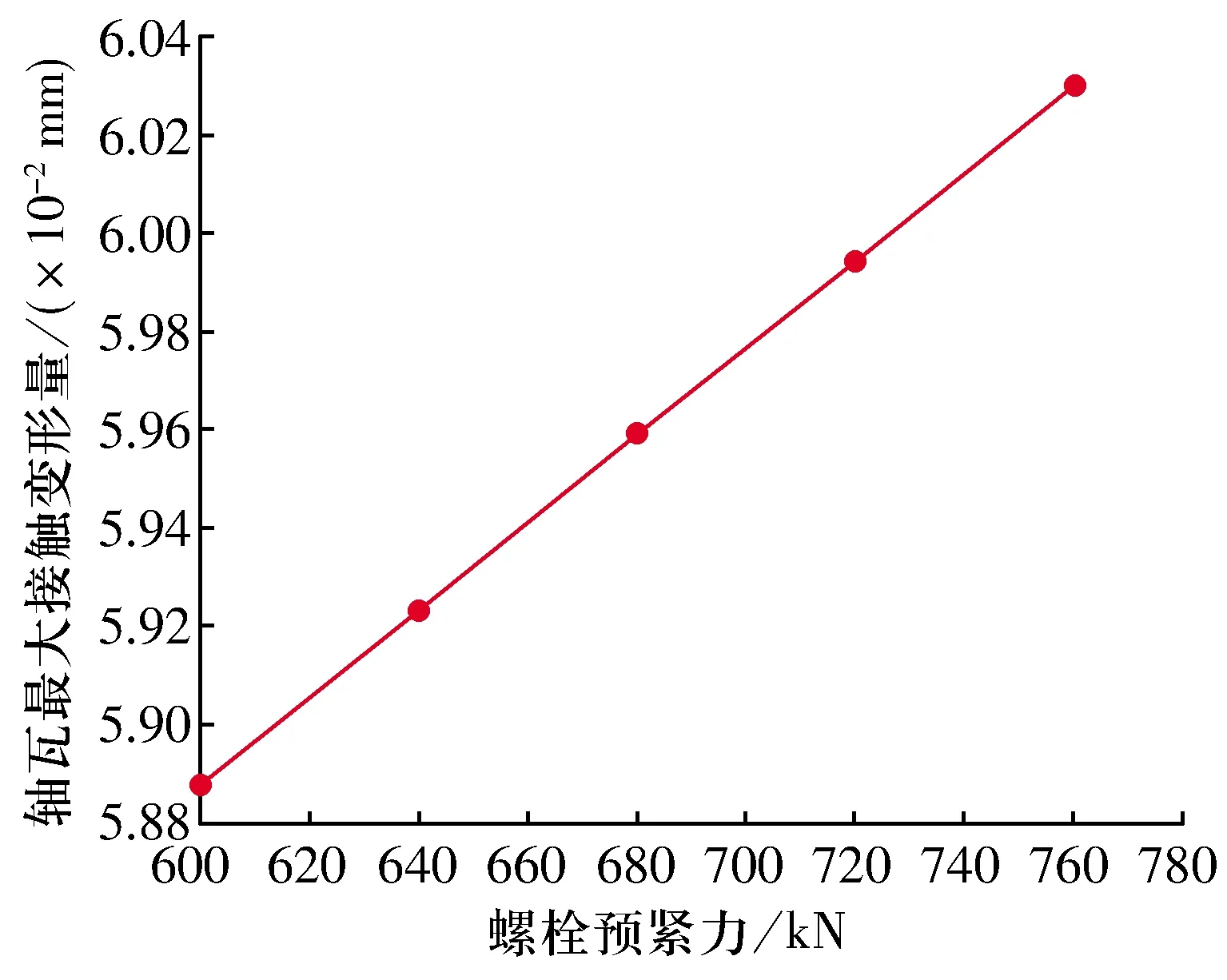
圖5 螺栓預緊力與軸瓦最大接觸變形量的關系Fig.5 Relationship between bolt preload and maximum contact deformation of bearing bush

2.1.2 過盈量對軸瓦最大接觸變形量的影響

在螺栓預緊力為640 kN，摩擦因數為0.3，氣體爆發壓力為406 397 N，過盈量u分別為0.20,0.22,0.24,0.26,0.28 mm的條件下進行數值模擬。不同過盈量下軸瓦變形量分布區域基本一致，但軸瓦最大接觸變形量差異較大，故取u為0.20，0.28 mm時的軸瓦變形量結果，如圖6所示。當u為0.20 mm時，軸瓦最大接觸變形量為4.992×10-2mm；當u為0.28 mm時，軸瓦最大接觸變形量為6.847×10-2mm，增加了37.1%。軸瓦變形量分布區域與螺栓預緊力的軸瓦變形量分布位置基本相同。

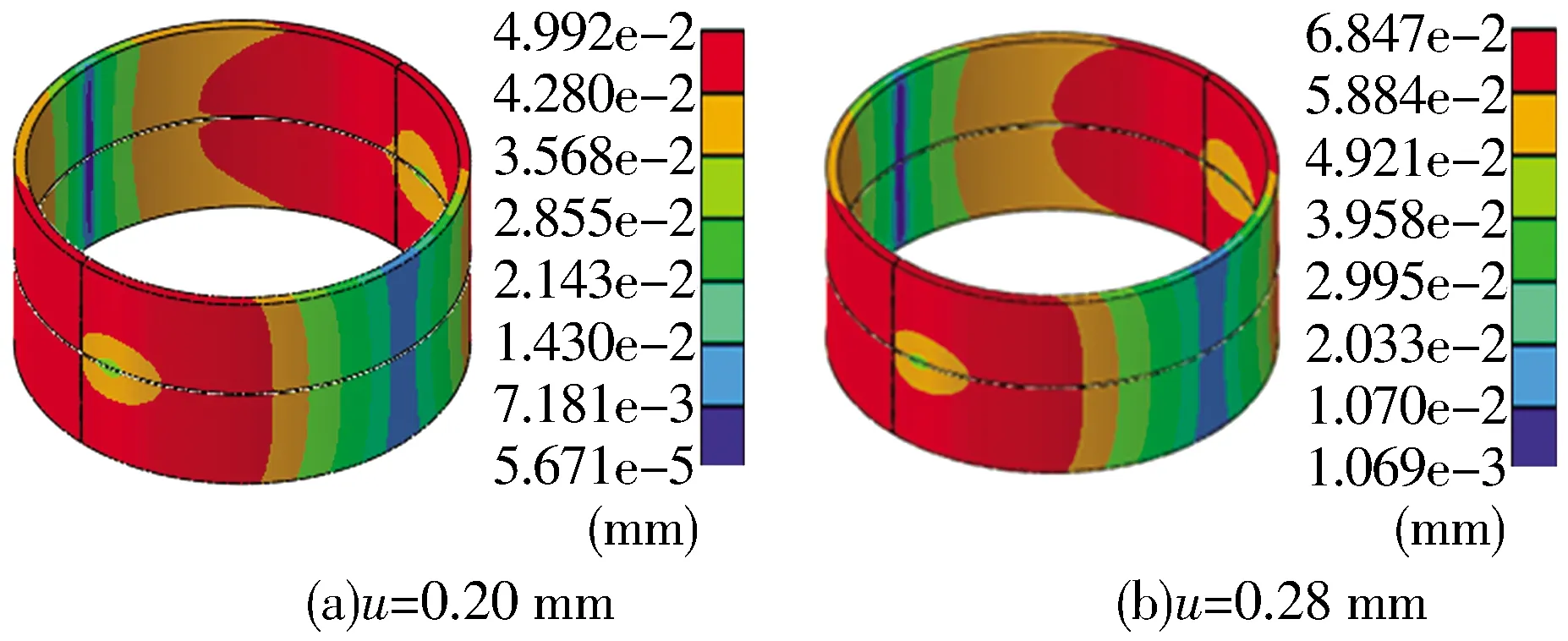
圖6 不同過盈量時軸瓦變形量分布Fig.6 Deformation distribution of bearing bush with different interferences

過盈量與軸瓦最大接觸變形量的關系如圖7所示，軸瓦最大接觸變形量隨過盈量增大而增大，這是因為軸瓦隨過盈量增大，等效應力增大，軸瓦采用錫青銅材料，因受力增大易發生變形[8]。軸瓦過盈量過大會導致軸瓦安裝困難且工作時接觸應力會超過軸瓦材料的屈服極限導致軸瓦失效；軸瓦過盈量過小會導致軸瓦與連桿大頭或軸瓦在孔座內發生滑動導致柴油機故障。

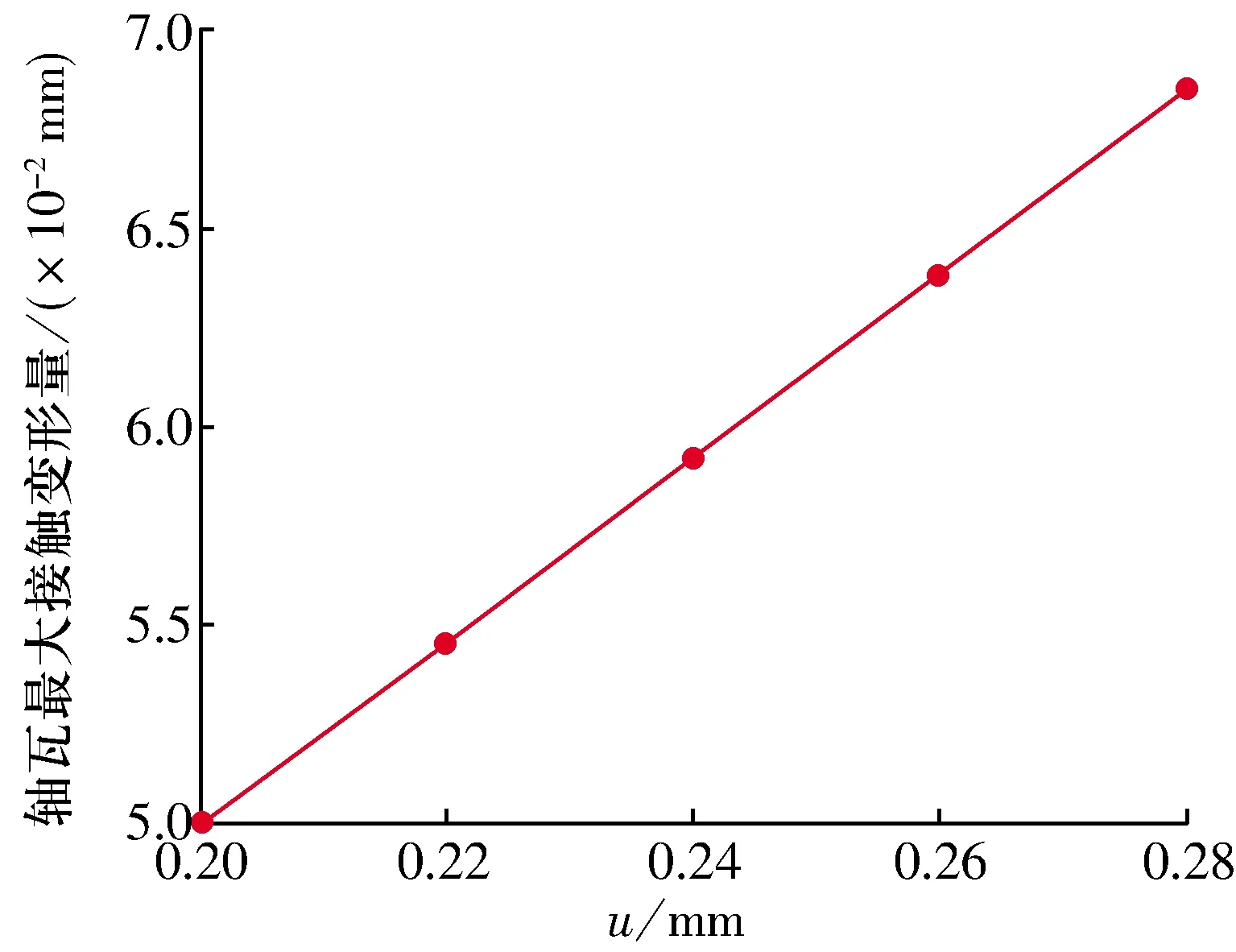
圖7 過盈量與軸瓦最大接觸變形量的關系Fig.7 Relationship between interference and maximum contact deformation of bearing bush

根據某柴油機部分參數在滿足軸瓦正常工作的條件下，過盈量取0.22～0.24 mm較合適。

2.1.3 摩擦因數對軸瓦變形量的影響

在螺栓預緊力為640 kN，軸瓦過盈量為0.24 mm，氣體爆發壓力為406 397 N，摩擦因數μ為0.2,0.3,0.4,0.5,0.6的條件下進行數值模擬。不同摩擦因數下軸瓦變形量分布區域基本一致，但軸瓦最大接觸變形量有差異，故取μ為0.2，0.6時的軸瓦變形量結果，如圖8所示。當μ為0.2時，軸瓦最大接觸變形量為5.956×10-2mm；當μ為0.6時，軸瓦最大接觸變形量為5.885×10-2mm，降低了1.2%；軸瓦變形量分布區域與研究螺栓預緊力、過盈量的軸瓦變形量影響時分布位置基本相同。

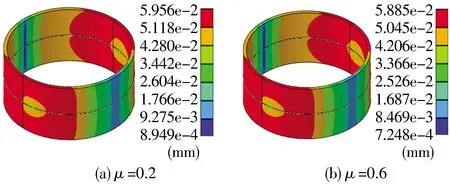
圖8 不同摩擦因數時軸瓦變形量分布Fig.8 Deformation distribution of bearing bush with different friction coefficients

摩擦因數與軸瓦最大接觸變形量的關系如圖9所示，軸瓦最大接觸變形量隨摩擦因數增大而呈減小趨勢，當μ為0.2～0.4時，隨摩擦因數增大，軸瓦最大接觸變形量急劇減小；當μ為0.4～0.6時，軸瓦與連桿大頭接觸面間摩擦力增大，軸瓦瓦背各節點位移變小使軸瓦整體變形量減小，進而使軸瓦最大接觸變形量的變化趨于平緩。摩擦因數過大導致軸瓦嚴重磨損，摩擦因數過小致使軸瓦最大接觸變形量增大，結合實際生產經驗，摩擦因數取0.4～0.5較合適。

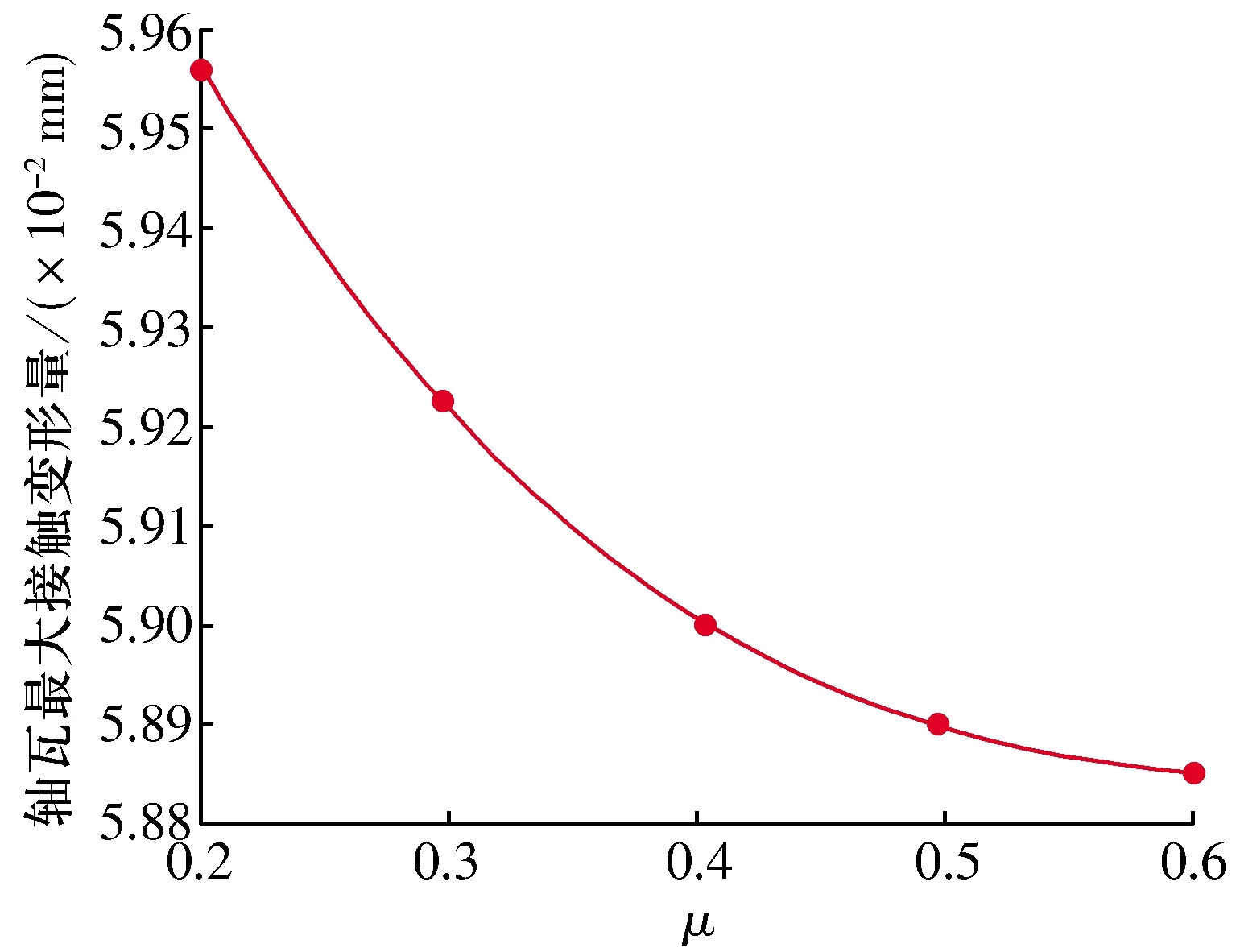
圖9 摩擦因數與軸瓦最大接觸變形量的關系Fig.9 Relationship between friction coefficient and maximum contact deformation of bearing bush

2.2 SPSS軟件正交試驗分析

以螺栓預緊力、過盈量、摩擦因數為考察因素，以軸瓦最大接觸變形量為考察指標，進行三因素三水平L9(33)正交試驗設計[9]。利用ABAQUS有限元軟件數值模擬表3中的9次試驗方案[10]，模擬得到軸瓦最大接觸變形量見表4。

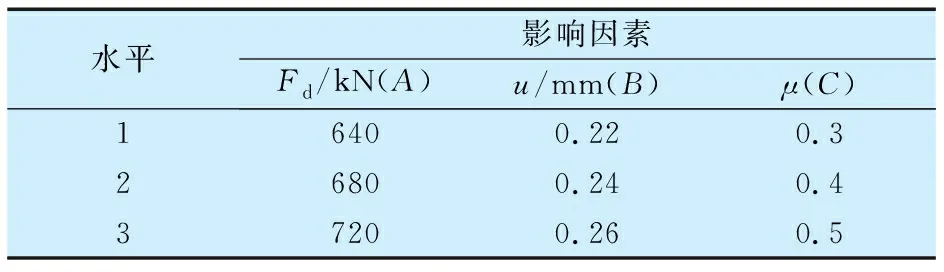
表3 軸瓦變形量有限元分析的因素水平表Tab.3 Factor level table for finite element analysis of bearing bush deformation

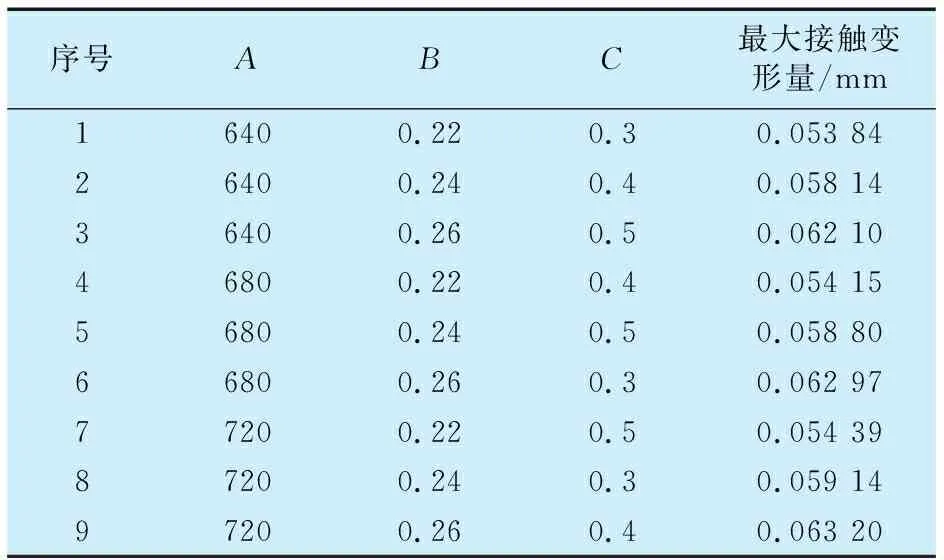
表4 軸瓦最大接觸變形量仿真結果Tab.4 Simulation results of maximum contact deformation of bearing bush

2.2.2 方差分析

利用SPSS軟件進行方差分析[11]，得到的結果見表5，其中df為自由度，F為組間均方與組內均方的比值，sig表示顯著性大小。

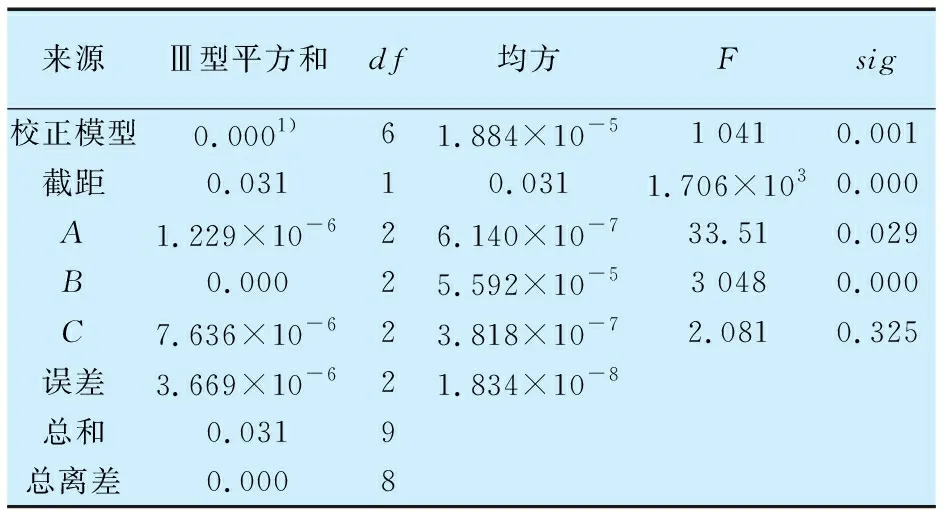
表5 單變量多因素方差分析Tab.5 Univariate multivariate analysis of variance

由于試驗中FB>FA>FC，(FA,FB,FC分別為螺栓預緊力、過盈量、摩擦因數在表5中所對應的F值)，則各因素對軸瓦最大接觸變形量的主次順序為B>A>C；因素Asig=0.029<0.05、因素Bsig=0.000、因素Csig=0.325>0.050，則因素A,B均對軸瓦最大接觸變形量有顯著性影響，而因素C無顯著性影響。

單變量多因素方差分析見表6，由表可知：A1均值最小(0.058 0)，且A3>A2>A1，則判斷A1為A的最優水平；B1均值最小(0.054 1)，且B3>B2>B1，則判斷B1為B的最優水平；而C對軸瓦最大接觸變形量無顯著性影響，摩擦因數過大導致軸瓦與連桿接觸面磨損增大，為避免軸瓦損害且滿足軸瓦正常工作，摩擦因數選取水平2。由此得出各因素對軸瓦最大接觸變形量的最優組合為A1B1C2，即螺栓預緊力為640 kN，過盈量為0.22 mm，摩擦因數為0.4。

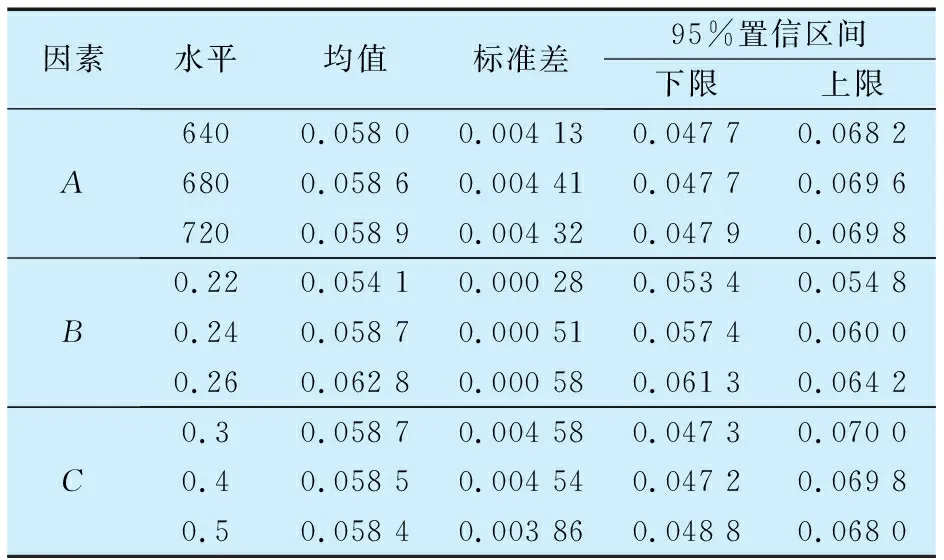
表6 單因素統計量表Tab.6 Single factor statistical scale

2.3 仿真對比

在螺栓預緊力為640 kN,過盈量為0.22 mm,摩擦因數為0.4(正交試驗選的最優數據組合)，氣體爆發壓力為406 397 N的條件下，運用有限元軟件ABAQUS模擬連桿極限工作狀態下軸瓦變形量，結果如圖10所示，軸瓦最大接觸變形量為5.379×10-2mm，優化后的結果小于正交試驗的最小值。

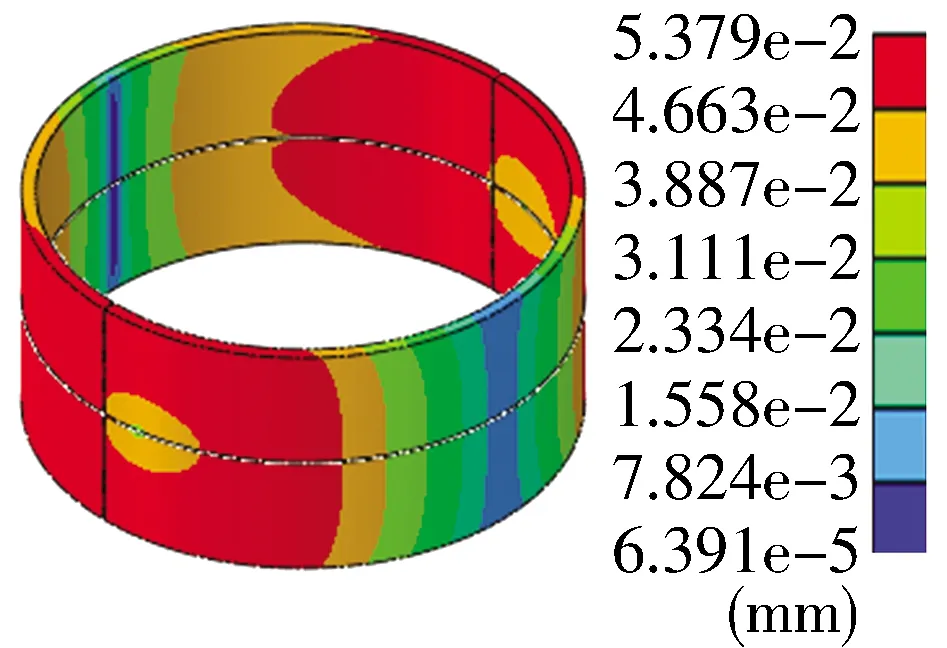
圖10 優化后軸瓦變形量分布Fig.10 Deformation distribution of optimized bearing bush

3 結論

運用ABAQUS有限元軟件對連桿-軸瓦摩擦副在最大爆發壓力下的最大接觸變形量進行模擬，設計正交試驗并考察螺栓預緊力、過盈量、摩擦因數對軸瓦最大接觸變形量的影響，并通過SPSS軟件對目標函數(軸瓦最大接觸變形量)進行優化，主要結論如下：

1)3種因素對軸瓦的最大接觸變形量均會產生一定的影響，影響的程度從大到小依次為過盈量、螺栓預緊力、摩擦因數。

2)過盈量和螺栓預緊力與軸瓦的最大接觸變形量基本呈正線性關系，而隨摩擦因數增大，軸瓦最大接觸變形量呈下降趨勢。

3)當螺栓預緊力為640 kN,過盈量為0.22 mm,摩擦因數為0.4時能夠有效減小軸瓦的最大接觸變形量，最大程度降低軸瓦碰撞的概率。