基于精細復合多元多尺度加權排列熵與流形學習的滾動軸承故障診斷

劉武強，申金星，楊小強

(陸軍工程大學 野戰工程學院，南京 210007)

滾動軸承是機械設備大量使用的部件，一旦發生故障，將會影響正常的工業生產甚至造成巨大損失[1]，因此探索軸承的故障機理和診斷技術具有工程實際意義。滾動軸承發生故障時，其振動信號會表現出強烈的非線性和非平穩性[2]，以傅里葉變換為代表的傳統方法無法處理此類信號，必須尋找更加有效的方法。

隨著香農熵理論的拓展，各種基于熵的理論被廣泛用于分析非線性時間序列[3-4]。多尺度熵(Multi-Scale Entropy，MSE) 采用的階躍函數在使用過程中會生成大量異常值，造成估計熵值不準確；多尺度排列熵 (Multi-Scale Permutation Entropy，MPE) 在衡量時間序列復雜性方面更具魯棒性，但其只考慮了時間序列的序數結構，忽略了振幅信息，多尺度加權排列熵(Multi-Scale Weighted Permutation Entropy，MWPE)針對此缺陷進行了改進[5]。然而，MPE和MWPE都是單變量分析方法，只利用了單一通道，其他通道的振動信息并未加以利用，可能會造成信息的丟失。文獻[6]在傳統單變量分析方法的基礎上，結合多維嵌入重構理論提出了多元多尺度排列熵(Multivariate Multi-Scale Permutation Entropy，MMPE)，以衡量多通道數據中時間序列的復雜性。MMPE不僅研究了多通道數據的動態關系，還綜合考慮多通道數據內部的非線性耦合特性。鑒于多通道信號分析的優勢，將MWPE擴展為多元多尺度加權排列熵(Multivariate MWPE，MMWPE)，但其在計算短時間序列以及較大尺度因子時得到的熵值會存在較大誤差[7]。針對該缺陷，本文采用精細復合多尺度的粗粒化方法，提出了精細復合多元多尺度加權排列熵(Refined Composite Multivariate Multi-Scale Weighted Permutation Entropy，RCMMWPE)，并將其用于提取滾動軸承的非線性故障特征。

通常，由RCMMWPE提取的特征是高維且冗余的，直接進行分類不僅耗時且效果不理想，有必要進行數據降維以獲得更好的分類效果。傳統降維方法對非線性數據的降維效果較差，無法揭示各數據之間的關聯性以及內部結構的特征。t分布隨機鄰近嵌入(t-distributed Stochastic Neighbor Embedding，t-SNE)[8]的性能優異，可視化效果好，適合揭示非線性數據的內部關系。

依據上述分析，采用RCMMWPE提取滾動軸承振動信號的故障特征，利用t-SNE對所獲取的特征進行降維以獲取相關性強的特征，同時結合隨機森林(Rand Forest，RF)構建多故障分類器進行滾動軸承故障診斷，并利用2類滾動軸承試驗數據進行分析驗證。

1 精細復合多元多尺度加權排列熵

1.1 多尺度加權排列熵

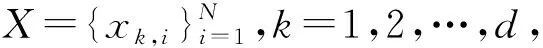
(1)

式中：m為嵌入維數；t為時間延遲。

(2)

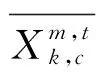
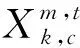
(3)

其中，MPE的相對頻率與時間序列的通道數有關。

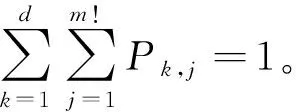
邊際相對頻率為

(4)

根據香農熵的定義，多尺度加權排列熵可以定義為

(5)

1.2 多元多尺度加權排列熵

多元多尺度加權排列熵的實現步驟如下[11]：

1)對于長度為N的d變量時間序列U={uk,b}，在尺度因子為τ時，其多元粗粒化時間序列為

(6)

多元多尺度加權排列熵通過將多元加權排列熵擴展至多個尺度獲得，可從不同尺度的多元粗粒度時間序列中獲得更多信息；但其采用的粗粒化方式存在缺陷，對于尺度因子τ只考慮了xk,1所包含的信息，而忽略了剩余τ-1的多元時間序列包含的信息。多元多尺度加權排列熵沒有考慮粗粒化時間序列之間的關系，從而導致了部分信息的丟失[12]。

1.3 精細復合多元多尺度加權排列熵

精細復合多元多尺度加權排列熵的具體步驟如下[13]：

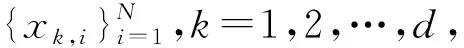
2)原始多元時間序列精細復合多元多尺度加權排列熵為

(7)

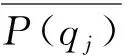
在精細復合多元多尺度加權排列熵算法中需要預先設置嵌入維數m、延遲時間t和尺度因子τ等參數。m太小會使重構向量中包含的狀態太少，算法失去有效性和意義，m過大則會將時間序列均勻化，增加計算量且無法反映時間序列內在的細微變化[14]，因此嵌入維數一般取3～7，本文取m=5。延遲時間t的影響可以忽略不計，通常取t=1。尺度因子τ的取值沒有限制，通常取τ≥10，本文取τ=20。

2 合成信號比較分析

高斯白噪聲和1/f噪聲是常用于進行復雜性分析的隨機信號[15]，考慮到普遍性，使用高斯白噪聲和1/f噪聲構造不同種類的多元信號：三通道高斯白噪聲信號、三通道1/f噪聲信號、一通道1/f噪聲和二通道高斯白噪聲信號、二通道1/f噪聲信號和一通道高斯白噪聲信號。每種狀態的合成信號采樣20組(長度為2 048)，通過分析合成信號來驗證RCMMWPE的性能，并與MMWPE、多元多尺度模糊熵(MMFE)和多元多尺度熵(MMSE)等多元分析方法進行對比。

上述4組多元合成信號的均值標準差如圖1所示，由圖可知：隨著尺度因子的增加，4種信號的MMWPE，MMFE和MMSE均出現較大的波動且在較大的尺度上有所重疊；RCMMWPE的標準差明顯小于MMWPE，表明RCMMWPE比MMWPE更穩定。相對而言，RCMMWPE具有更好的分離能力和穩定性，在多元信號特征提取方面更具優勢，能夠有效區分多元信號的復雜性。

圖1 多元合成信號的計算結果Fig.1 Calculation results of multivariate synthetic signals

3 軸承故障診斷方法

3.1 故障診斷流程

在特征提取時，數據的多樣性會導致數據本身對特征向量有所偏好，即同一種特征向量在不同數據下的診斷效果可能不是當前數據中最優的診斷結果，為此需要提取大量的特征；但增大特征向量維度可能會包含部分冗余信息，從而影響故障分類和診斷效率。隨機森林作為比較經典的集成學習算法，能夠解決SVM對處理大批量數據能力不足的缺點，從高維數據中充分挖掘與故障有關的特征信息以提高分類準確率[16-17]。因此，提出了基于RCMMWPE，t-SNE和RF的滾動軸承故障診斷方法，其實現流程如圖2所示，具體步驟如下：

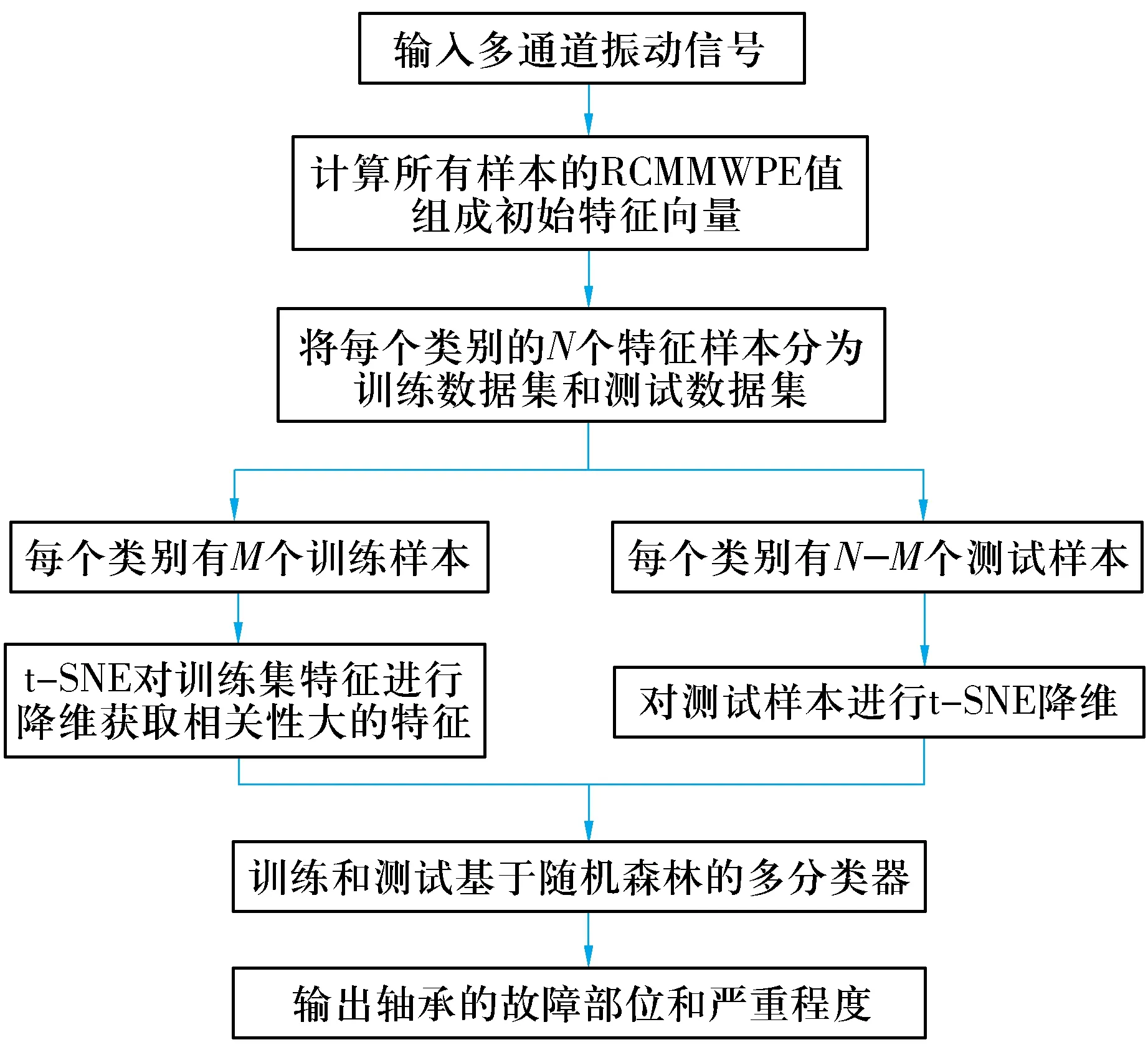
圖2 基于RCMMWPE，t-SNE和RF的滾動軸承故障診斷流程Fig.2 Flow chart of fault diagnosis for rolling bearings based on RCMMWPE,t-SNE and RF

1)選取Y種不同故障狀態的滾動軸承振動信號，每種狀態有M個樣本。

2)計算所有樣本的RCMMWPE，將20個尺度的特征值作為故障特征向量。

3)利用具有良好非線性降維能力的t-SNE對故障特征向量進行降維。

4)將降維后的故障特征向量輸入到RF多故障分類器進行訓練。

5)將測試樣本輸入到訓練好的多故障分類器進行分類，實現滾動軸承的故障診斷。

3.2 試驗數據分析

3.2.1 案例一

采用美國西儲凱斯大學軸承數據中心的軸承數據，軸承型號為SKF6205，通過電火花加工在軸承內、外圈(6點鐘方向)及鋼球上設置單點故障，具體故障類型及故障程度見表1。在1 797 r/min轉速及0負載工況下，以12 kHz的采樣頻率采集驅動端和風扇端的同步振動信號作為雙通道數據，其時域波形如圖3所示。其中每個振動信號均被分為多組不重疊的數據樣本，以形成由每種狀態下各58個樣本組成的試驗數據集。

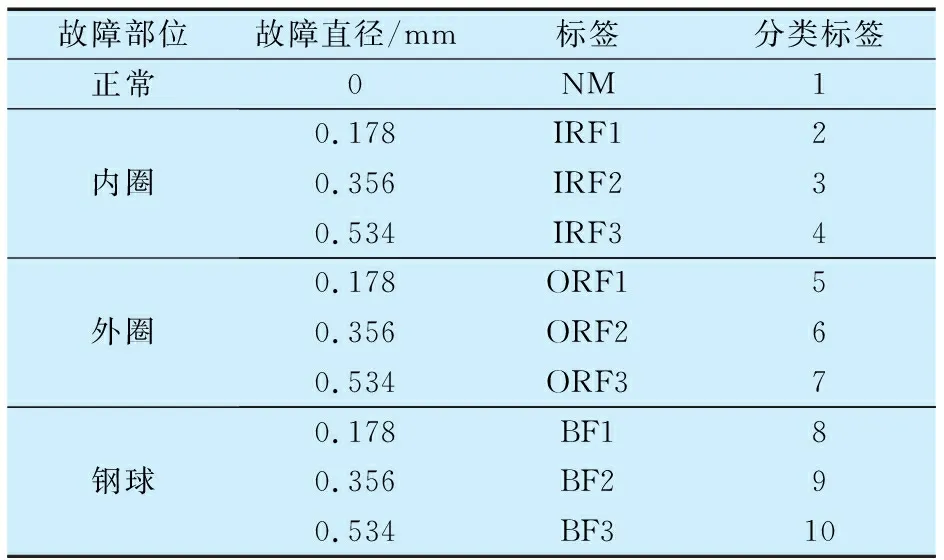
表1 滾動軸承故障尺寸及分類Tab.1 Fault size and classification of rolling bearings

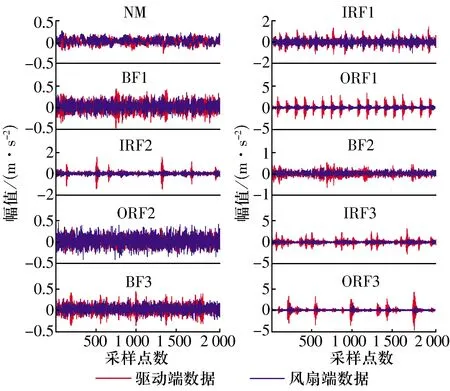
圖3 雙通道SKF6205軸承振動信號的時域波形Fig.3 Time domain waveform of two-channel SKF6205 bearing vibration signals

分別采用RCMMWPE，MMWPE，MMFE，MMSE，MWPE和多尺度模糊熵(MFE)對10種狀態的多通道振動信號進行對比分析，其中基于單通道振動信號分析的MWPE采用驅動端振動信號。10種狀態軸承振動信號(每組15個樣本)的均值標準差曲線如圖4所示，由圖可知：

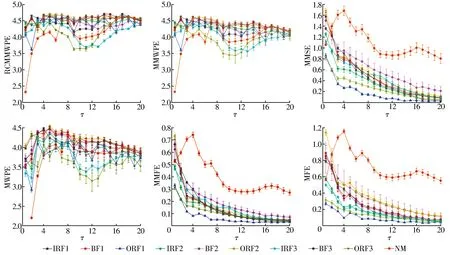
圖4 不同狀態SKF6205軸承振動信號的計算結果Fig.4 Calculation results of SKF6205 bearing vibration signals under different states

1)在相同的尺度下，MMWPE的ORF3曲線標準差略小于MWPE，表明MMWPE在量化振動信號復雜性方面具有比MWPE更好的性能；而MMFE的BF2曲線標準差也要顯著小于MFE的BF2曲線。這2個對比驗證了雙通道分析方法優于單通道分析方法。

2)RCMMWPE曲線各個狀態的標準差都明顯小于MMWPE，表明經過RCMMWPE提取的特征具有更高的穩定性。與雙通道的MMFE和MMSE相比，RCMMWPE更穩定，誤差也比其他方法要小,總體性能更佳。

此外，在尺度因子為1時，正常滾動軸承的RCMMWPE值較小，可見多元加權排列熵能夠將故障軸承和正常軸承區分開。在此情況下，若要判斷軸承是否故障，設定閾值0.5即可以有效的檢測軸承是否故障，對實際運行條件下的軸承健康檢測有一定的意義。

為準確判斷滾動軸承的運行狀態，將基于RCMMWPE，t-SNE和RF的故障診斷方法應用于上述試驗數據進行分析。每種狀態各58組樣本，每組樣本20個特征，組成R580×20的特征空間，隨后利用t-SNE算法進行特征約簡得到低維特征空間R580×2，結果如圖5所示，每種故障特征都有較好的聚類特性，說明所提取的特征質量較高，能夠有效地區分故障狀態。

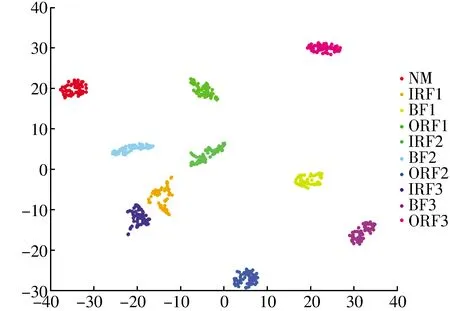
圖5 低維故障特征可視化圖(SKF6205)Fig.5 Visualization of low-dimensional fault feature(SKF 6205)

將降維后的特征樣本送入到RF分類器進行故障分類。選擇380組樣本進行訓練，剩余樣本的測試結果見表2，由表可知：除了內圈故障中的一個樣本被錯分為鋼球故障，其余樣本都準確劃分了故障類型，總體識別率達到了99.5%，說明本文所提方法不僅能夠準確判斷軸承運行狀態，還可以有效判斷軸承的故障程度。

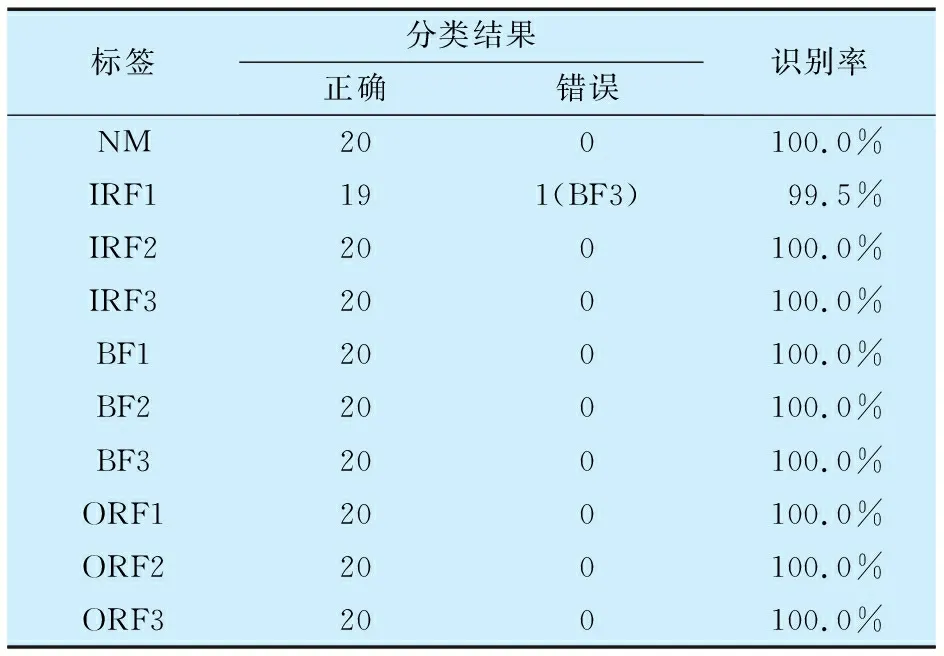
表2 RF分類器對RCMMWPE+t-SNE故障診斷方法的識別率Tab.2 Recognition rate of RF classifier to fault diagnosis method of RCMMWPE+t-SNE

為進一步證明RCMMWPE在特征提取方面的優越性，采用不同特征提取算法結合t-SNE和RF分類器對相同數量的樣本進行分類，結果見表3，由表可知：無論是單通道還是雙通道的特征提取算法，其錯分數均遠遠大于RCMMWPE算法，RCMMWPE算法的故障識別率最高。

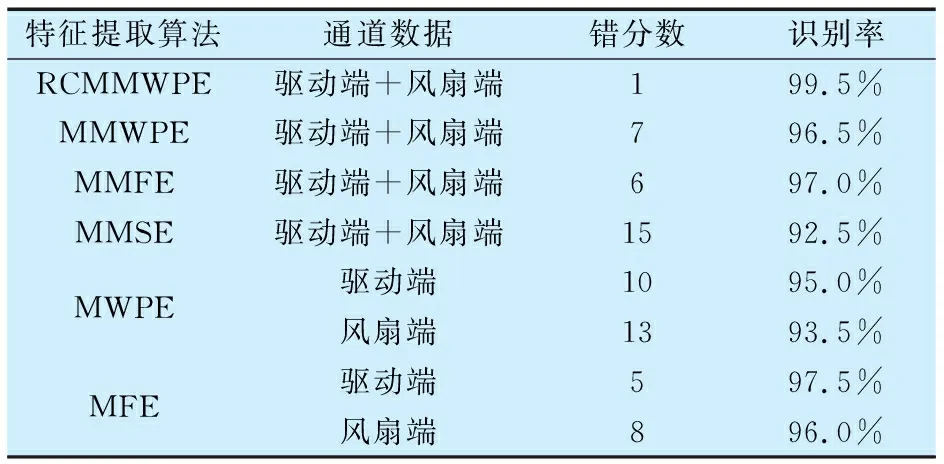
表3 不同特征提取算法與t-SNE及RF分類器結合后的診斷結果Tab.3 Diagnostic results of different feature extraction algorithms combined with t-SNE and RF classifiers

3.2.1 案例二

為了說明本文所提方法對于滾動軸承故障診斷的普適性，采用西安交通大學的滾動軸承試驗數據[18]進行泛化性驗證，試驗軸承型號為LDK UER204，其參數見表4。采樣頻率為25.6 kHz，每1 min記錄32 768個樣本，通過分別放置在垂直軸、水平軸上互成90°的2個PCB352C33加速度計采集同步振動信號作為雙通道數據。設置了正常(NM)，內圈故障(IRF)，外圈故障(ORF)和保持架故障(CF)共4種故障類型，每個故障類型的樣本包含2 048個數據點，每個數據文件分為16組樣本，不同故障類型滾動軸承雙通道振動信號的時域波形如圖6所示。每個振動信號均被分為多組不重疊的數據樣本，以形成由每種狀態各58個樣本組成的數據集。

表4 測試軸承的基本參數

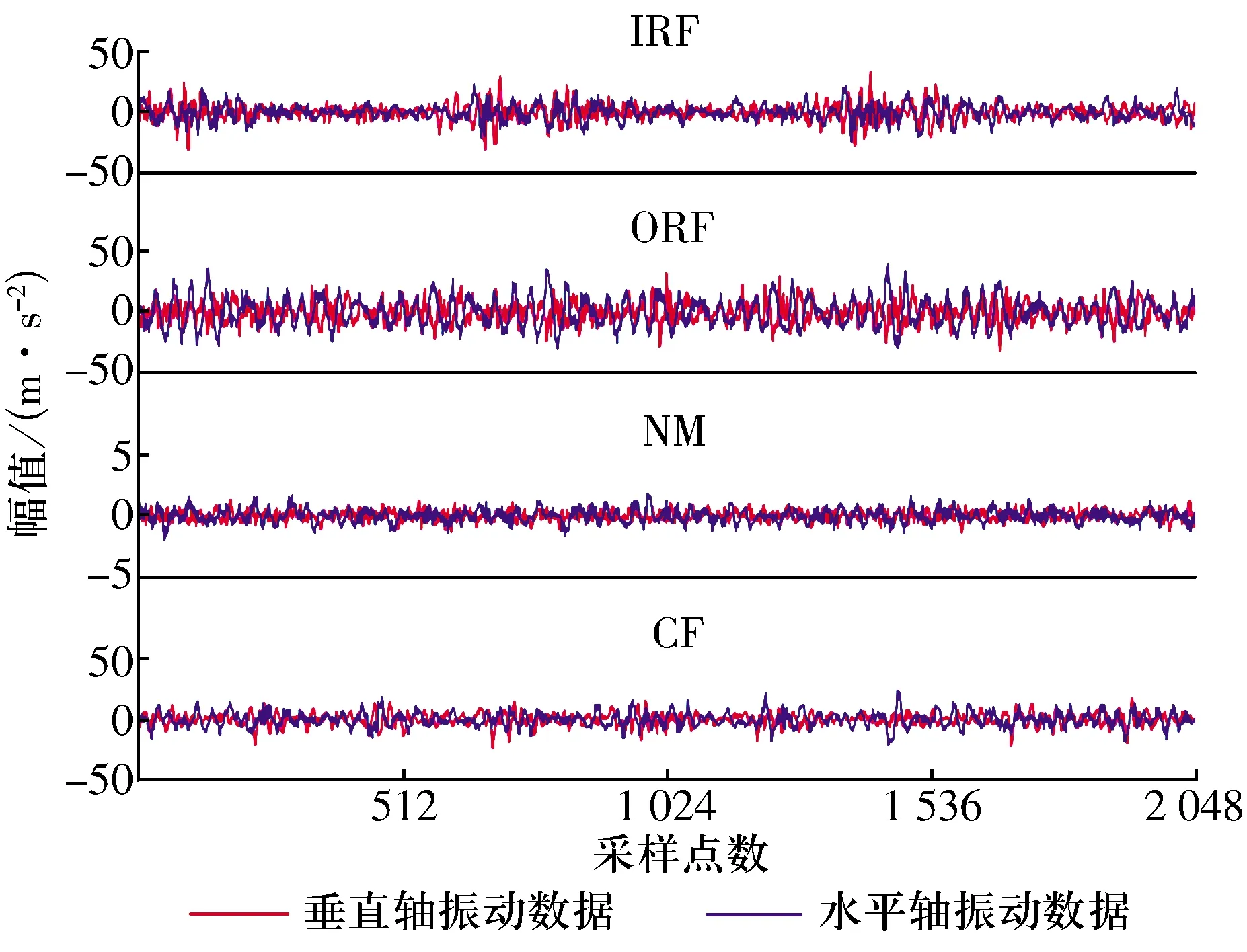
圖6 不同故障狀態LDKUER204軸承振動信號的時域波形Fig.6 Time domain waveform of LDKUER204 bearing vibration signals under different fault states

同樣，采用方案一的流程對軸承振動信號進行處理及對比分析，結果分別如圖7、圖8及表5所示。分析可知：RCMMWPE方法由于利用了多個通道的振動信息，能夠提高故障信息的利用率，提高了特征質量，相對于其他幾種方法具有更好的特征提取性能；經t-SNE降維后，每種故障特征都有較好的聚類特性，故障分類效果較好；在RF分類器中的識別率達到了100%，遠遠高于其他特征提取算法。

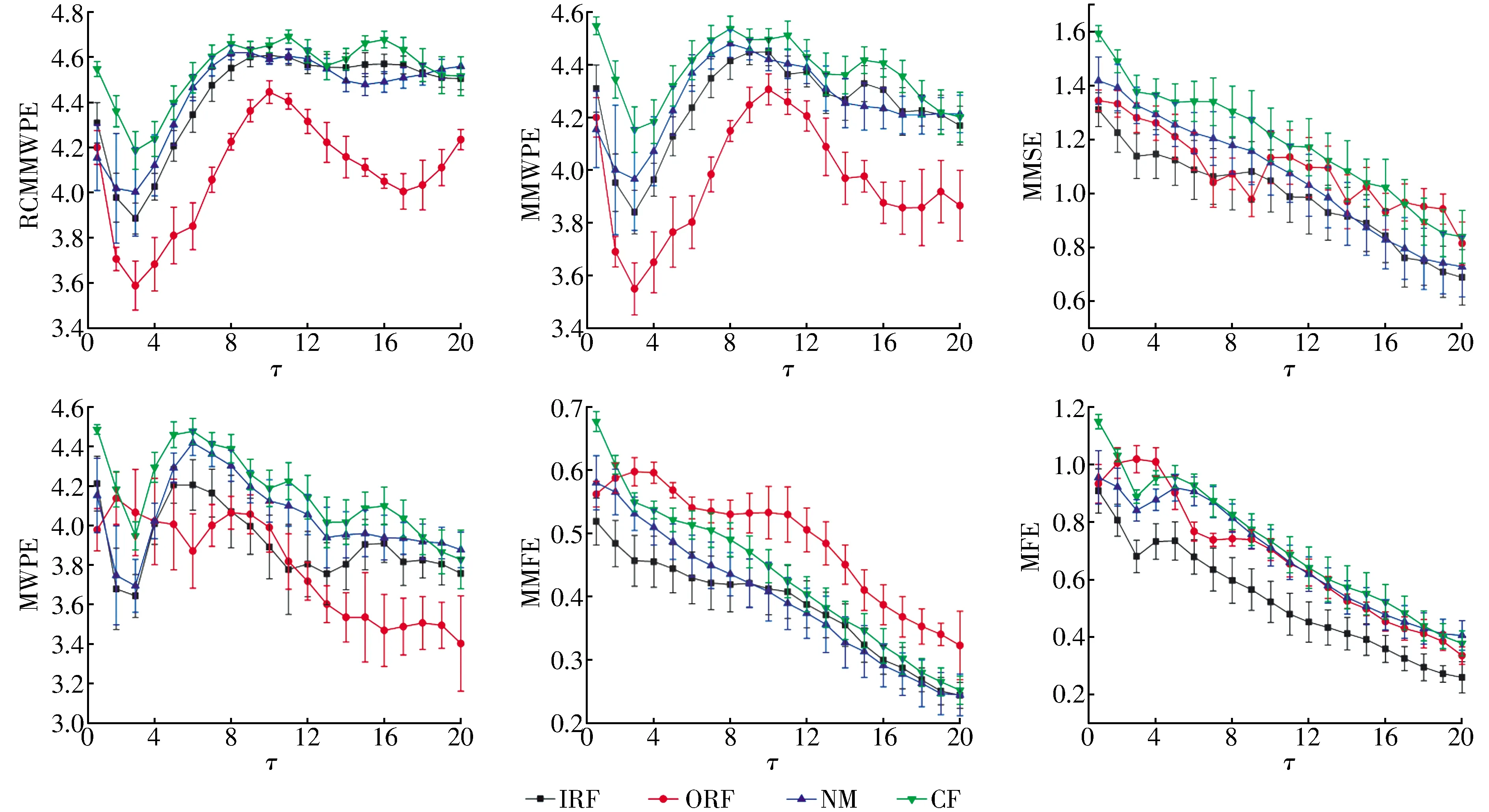
圖7 不同故障狀態LDKUER204軸承振動信號的計算結果Fig.7 Calculation results of LDKUER204 bearing vibration signals under different fault states

圖8 低維故障特征可視化圖(LDKUER204)Fig.8 Visualization of low-dimensional fault feature(LDKUER204)

表5 不同算法的故障識別率Tab.5 Fault recognition rate of different methods

4 結束語

提出了精細復合多元多尺度加權排列熵作為一種測量多通道數據相關性和復雜度的新型非線性動態方法。通過分析多通道合成信號，將提出的RCMMWPE方法與MMSE，MMFE和 MMWPE進行了比較，結果表明，所提出的RCMMWPE在特征提取穩定性和準確性方面具有優勢。基于此，提出了基于RCMMWPE和t-SNE進行特征提取和隨機森林分類的滾動軸承故障診斷方法。通過對2種類型的滾動軸承試驗數據進行分析，將所提出的方法與單通道MWPE，MFE及多通道MMSE，MMFE和MMWPE方法進行了比較，分析結果表明，所提出的滾動軸承故障診斷方法具有比現有故障診斷方法更高的故障識別率，同時具有更好的泛化性，能夠用于不同種類軸承數據的故障診斷。