油腔結構對液體靜壓推力軸承承載力的影響
田助新,李波
(1.三峽大學 機械與動力學院,湖北 宜昌 443002;2.華中科技大學 機械科學與工程學院,武漢 430074;3.襄陽華中科技大學先進制造研究院,湖北 襄陽 441053)
液體靜壓推力軸承以其旋轉精度高,油膜剛度大,減振性好等優點在重載支承領域占有重要地位[1],被廣泛應用于機床、泵、定位臺、望遠鏡、測量設備、測功器和雷達天線等領域[2-3]。
文獻[1]提出了一種計算非牛頓流體潤滑的圓形油腔液體靜壓推力軸承靜態特性的新方法,通過對油膜沿半徑方向的速度做均化處理,使分析過程大為簡化。文獻[2]針對圓形油腔液體靜壓推力軸承計算結果與試驗結果存在較大差異的問題,在考慮供油孔區域慣性效應的前提下重新計算,縮小了理論計算與試驗之間的差異,指出不能忽視小徑軸承供油孔區域的慣性效應。文獻[4]通過分形理論對液體靜壓推力軸承表面形貌進行了仿真模擬,并通過試驗對仿真結果進行驗證,結果表明表面粗糙度和平面度綜合特征的模擬符合真實情況。文獻[5]研究了多油腔液體靜壓推力軸承的剛度特性,結果表明不能忽視潤滑油黏度對剛度的影響。文獻[6]討論了油腔結構對油膜溫升的影響,結果表明矩形油腔的溫升最小。文獻[7]分析了油腔尺寸對機床靜壓軸承溫度場的影響,結果表明油腔深度對溫度場的影響最大。
上述研究均未涉及油腔結構對液體靜壓推力軸承承載能力的影響,因此,本文對不同油腔結構下液體靜壓推力軸承承載能力的差異進行探討。
1 油腔結構
液體靜壓推力軸承承受軸向載荷,通過高壓油膜將軸承與轉軸隔開,起到減小摩擦的作用。3種液體靜壓推力軸承(簡稱推力軸承)的結構如圖1所示。圖1a中的圓形油腔推力軸承以軸承中心為圓心開有圓形油腔,ra0為供油孔半徑,ra1為油腔半徑,R為軸承外半徑,h為封油邊油膜厚度,βh為油腔區域油膜厚度,Ps為供油壓力;圖1b中的環形油腔推力軸承以軸承中心為圓心開有環形油腔,rb0為軸承內徑,rb1為環形油腔內徑,rb2為環形油腔外徑,rb3為供油孔位置;圖1c為扇形油腔推力軸承,本文為常見的四油腔結構,以軸承中心為圓心開有4個扇形油腔,其均勻分布在一個同心圓上,rc0為軸承內徑,rc1為環形油腔內徑,rc2為環形油腔外徑。

圖1 3種油腔結構的液體靜壓推力軸承示意圖
2 分析過程
忽略油膜體積力,只考慮油膜沿半徑方向的慣性力,在柱坐標系下推力軸承的穩態雷諾方程為
(1)
式中:P為油膜壓力;r為油膜半徑;θ為周向坐標;ρ,η分別為潤滑油密度和黏度;ω為軸承轉速。
為簡化計算過程,引入量綱一的量,即
(2)
式中:S為軸承慣性參數;W為油膜承載力。將(2)式代入(1)式,可得
(3)
圓形和環形油腔推力軸承的油膜沿豎直方向呈軸對稱分布,油膜壓力沿圓周方向不會發生變化,即(3)式等號左邊第2項為零,因此,其雷諾方程為
(4)
(4)式為一元微分方程,可直接求解,即
P*=Sr*2+C1lnr*+C2,
(5)
式中:C1,C2為積分常數,由軸承的壓力邊界條件確定。
2.1 圓形油腔推力軸承
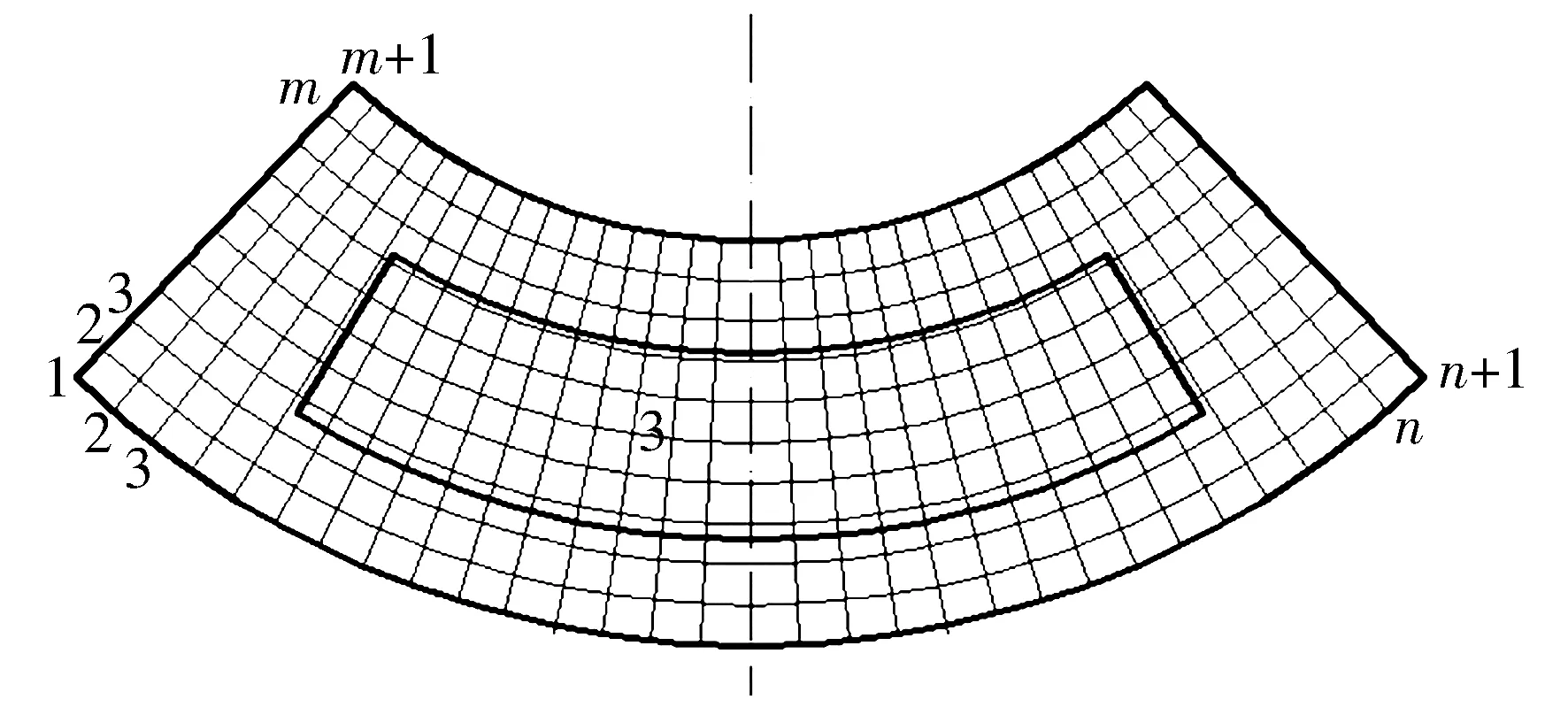
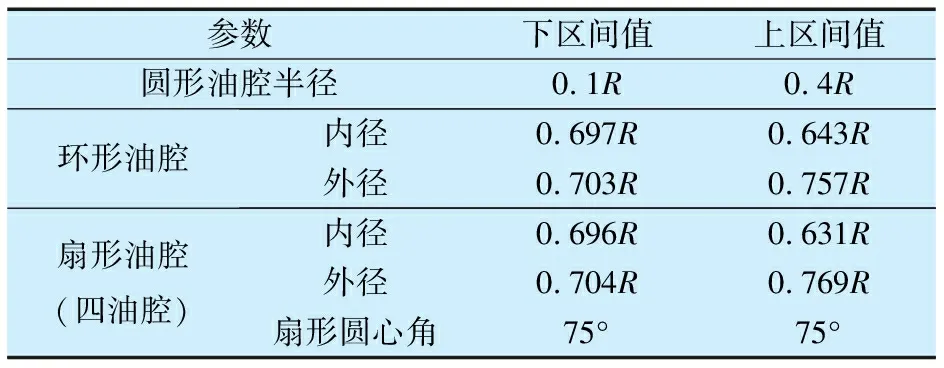
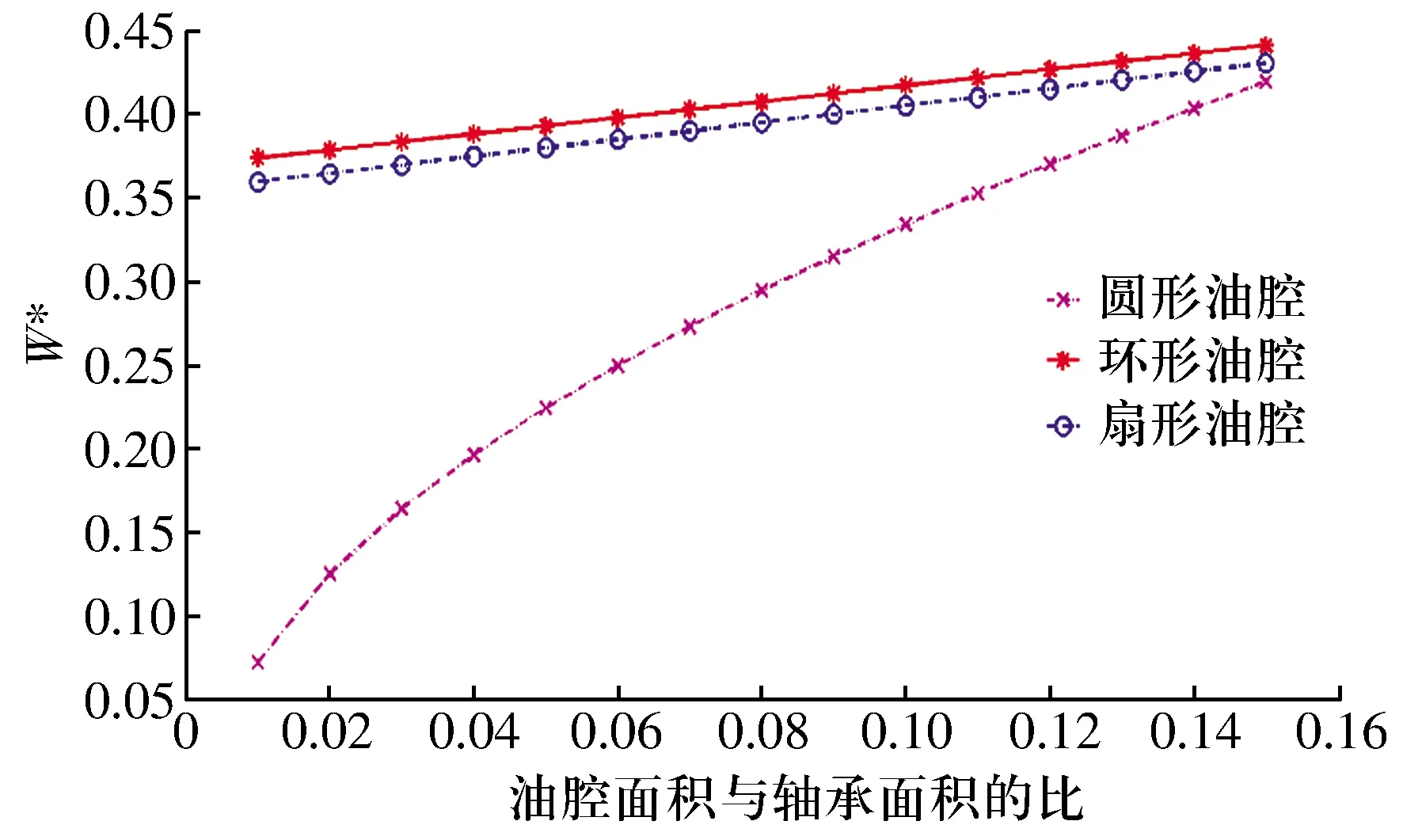
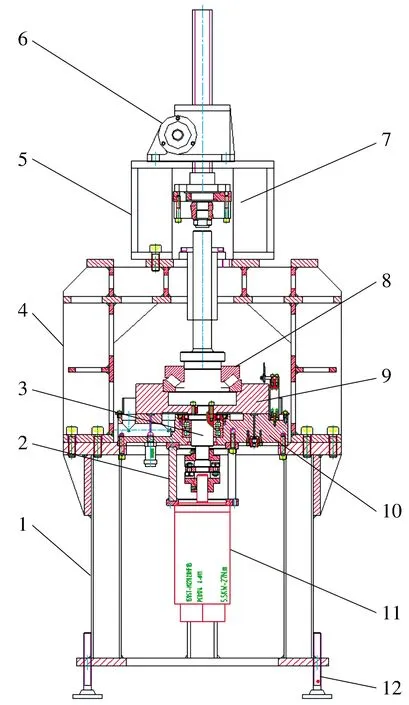
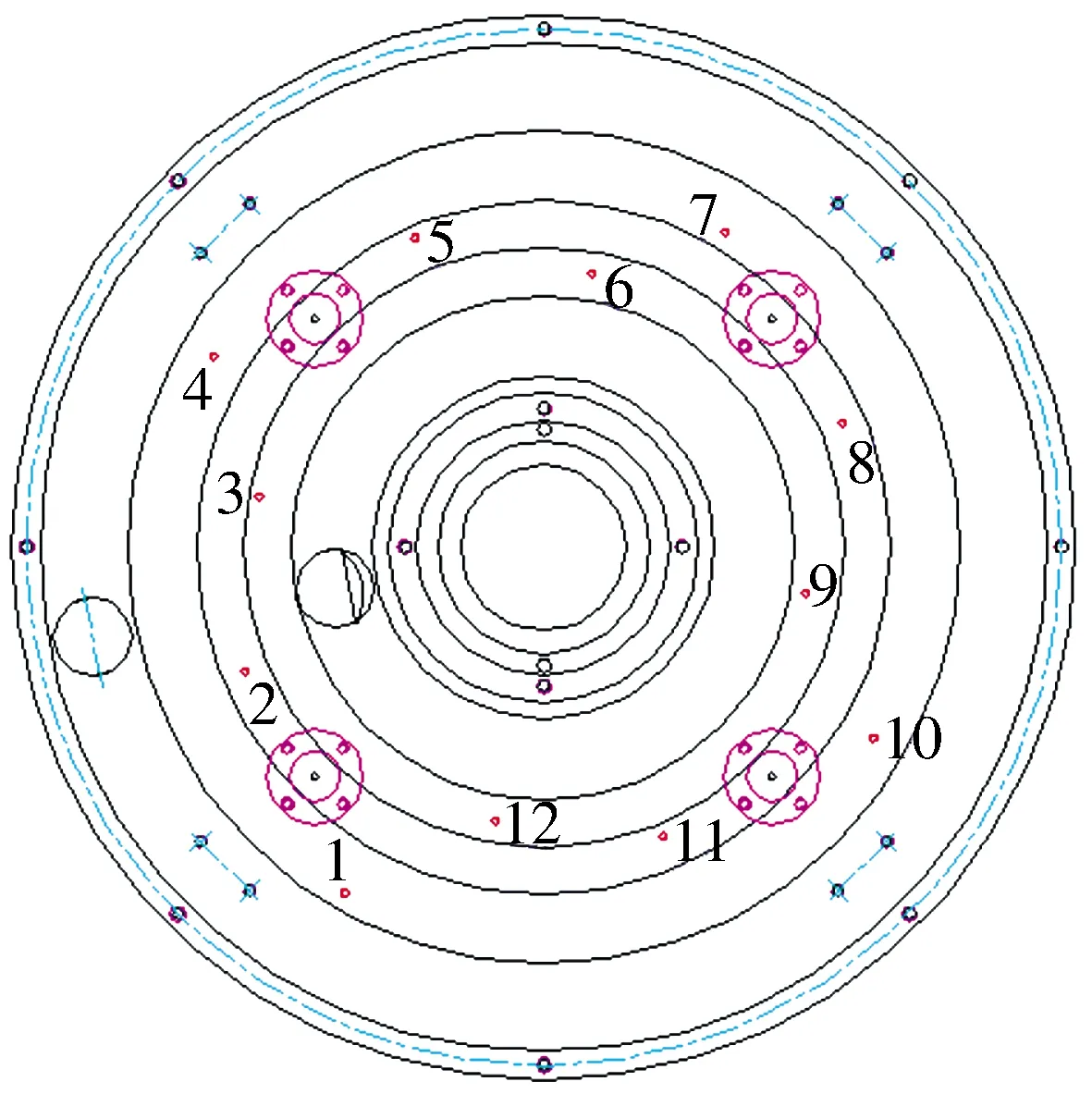
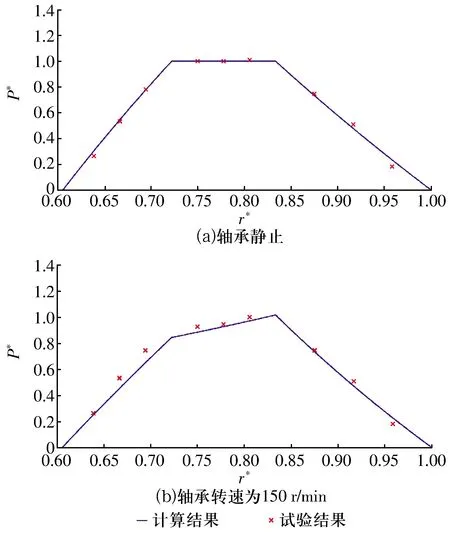
可將油膜區域分為供油孔區域(0≤r≤ra0)、油腔區域(ra0 P*= (6) 式中:Ci(i=1,2,3,4)為積分常數。引入油膜壓力的2個邊界條件,即 (7) (6)式共有4個未知數,因此在上述2個邊界條件的基礎上,再補充油膜壓力和流量在r=ra1處的連續條件,可求得壓力分布為 (8) 式中:β為油腔處油膜厚度與封油邊處油膜厚度的比值。 將壓力在量綱一的油膜半徑0~1上積分可得到油膜承載力為 (9) 環形油腔與軸承的圓心相同,潤滑油通過進油孔進入油腔后分別向內、外方向卸油。與圓形油腔推力軸承類似,考慮潤滑油的慣性效應時油膜壓力由供油系統油壓P1和轉動產生的慣性壓力P2組成。 求解供油系統的油壓P1時,不考慮軸承轉動帶來的影響,因此S=0,并且油腔壓力恒定,此時P1為 (10) 邊界條件為 (11) 由此可解得 (12) 求解轉動產生的慣性壓力P2時,可將油膜區域分為內封油面區域(rb0≤r≤rb1)、油腔區域(rb1 (13) 此時,只有2個壓力邊界條件,即 (14) 再補充油腔邊界r=rb1和r=rb2處的壓力和流量連續條件,即可求解(13)式中的6個未知數,即 (15) 2.2.3 推力軸承的油膜總壓力和承載力 油膜總壓力為 (16) 油膜總壓力對面積積分得到承載力為 (17) (3)式為扇形油腔推力軸承量綱一的油膜壓力限制方程其為二階偏微分方程,無法求得解析解,需通過數值法求解。 由于4個油腔沿圓周均勻分布,以油腔3為對象對油膜劃分網格,如圖2所示,將其在徑向m等分,每段長度為Δr,沿圓弧方向n等分,每段長度為Δθ,m和n的值根據實際情況確定。設Pi, j(i=1,2,…,m+1;j=1,2,…,n+1)為任意點的壓力值,運用中間差分公式可得 圖2 油腔3的油膜網格劃分示意圖 (18) (19) 將(18)式和(19)式代入(3)式整理可得 (20) 將各微分區域上的壓力與面積相乘后累加,得到油膜承載力,即 (21) 式中:k為油腔個數,k=4。 為說明油腔結構對推力軸承承載力的影響,將3種推力軸承的油腔面積設為相等,3種結構推力軸承的幾何參數見表1。 表1 3種結構推力軸承的幾何參數 由圖3可知,當3種推力軸承的油腔面積相等時,環形油腔軸承承載力最大,圓形油腔軸承承載力最小,原因為:對于圓形油腔軸承,油膜的慣性效應會加快潤滑油卸油,進而減小承載力;對于環形油腔,油膜的慣性效應會阻礙內封油面區域的卸油,承載力增大;隨著油腔面積的增大,封油面占比縮小,承載力受油腔區域承載能力的影響逐漸變大,3種軸承承載力之間的差距逐漸縮小。 圖3 推力軸承承載力與油腔面積關系 為驗證上述分析的正確性,在環形油腔液體靜壓推力軸承試驗臺上測量承載力(試驗條件有限,只搭建了環形油腔推力軸承試驗臺對性能最優的環形油腔推力軸承進行驗證),試驗臺如圖4所示,環形油腔推力軸承如圖5所示,其結構參數見表2。 1—下支座;2—電動機安裝架;3—主軸;4—上支架;5—支承架;6—加載手柄;7—蝸輪蝸桿加載機構;8—推力調心滾子軸承;9—回轉臺;10—環形油腔推力軸承;11—主軸電動機;12—螺紋支承腳 圖5 環形油腔推力軸承 表2 環形油腔推力軸承幾何參數 為測量軸承工作時的壓力分布,在推力軸承上布置了12個壓力傳感器,傳感器量程為10 MPa,精度為0.01 MPa,分辨率為0.001 MPa,其具體分布情況如圖6所示,在內封油面、油腔和外封油面每間隔90°各設置4個:內封油面上的4個壓力點為3,6,9,12,其中點3布置在半徑為125 mm的圓上(量綱一的徑向坐標值為0.69),點6,12都布置在半徑為120 mm的圓上(量綱一的徑向坐標值為0.67),點9布置在半徑為115 mm的圓上(量綱一的徑向坐標值為0.64);油腔區域的4個點為2,5,8,11,其中點2,8都布置在半徑為140 mm的圓上(量綱一的徑向坐標值為0.78),點5布置在半徑為145 mm的圓上(量綱一的徑向坐標值為0.81),點11布置在半徑為135 mm的圓上(量綱一的徑向坐標值為0.75);外封油面上的4個點為1,4,7,10,其中點1布置在半徑為172.5 mm的圓上(量綱一的徑向坐標值為0.96),點7布置在半徑為157.5 mm的圓上(量綱一的徑向坐標值為0.88),點4,10布置在半徑為165 mm的圓上(量綱一的徑向坐標值為0.92)。 圖6 壓力傳感器分布示意圖 受試驗臺條件的限制,當轉速超過150 r/min,壓力傳感器的讀數跳動太大,測量結果可靠性不足,因此,將軸承轉速設為150 r/min。 具體試驗過程為:1)軸承靜止時,通過供油孔給油腔供油,供油壓力設置為1.2 MPa,待壓力傳感器讀數穩定后轉動加載手柄,通過蝸輪蝸桿加載機構沿豎直方向對軸承施加4 900 N(500 kg)的載荷,讀取12個位置壓力傳感器的壓力值;2)撤除載荷,保持供油壓力不變,啟動主軸電動機,將主軸轉速調整到150 r/min,沿豎直方向對軸承施加1 470 N(150 kg)的載荷,讀取12個位置的壓力值。 試驗值與理論計算值如圖7所示,當軸承靜止時,試驗值與理論計算值的一致性良好;當軸承以150 r/min轉動時,試驗值與理論值較為符合,誤差保持在8%以內,說明了本文理論分析的正確性。 圖7 環形油腔推力軸承油膜壓力計算值與試驗值對比 討論了推力軸承油腔結構(圓形、環形和扇形)對其承載力的影響,通過理論分析得到3種油腔結構的推力軸承承載力,通過對比發現:在油腔面積相同時,環形油腔推力軸承承載力優于圓形和扇形油腔軸承。在環形油腔液體靜壓推力軸承試驗臺上測得軸承油膜壓力分布與本文理論計算結果基本一致,說明本文理論分析的正確性。在需較大承載能力的情況下,液體靜壓推力軸承的油腔結構可優先選擇環形油腔。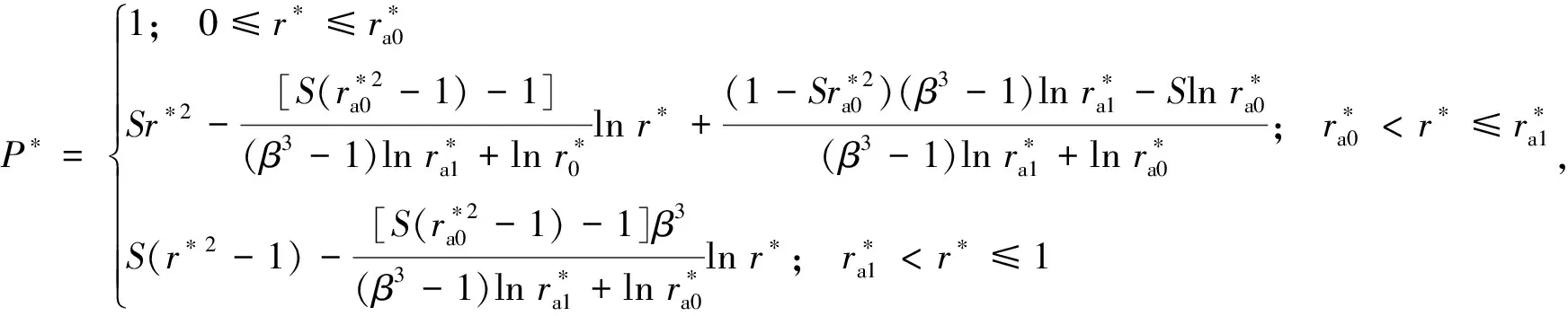
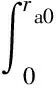
2.2 環形油腔推力軸承
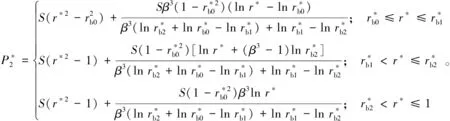
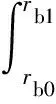
2.3 扇形油腔推力軸承
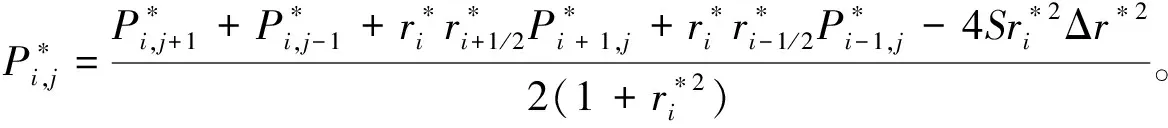
2.4 結果對比
3 試驗驗證


4 結束語

