修正Broer-Kaup-Kupershmidt (mBKK)方程組的李對稱分析,非線性自伴隨及守恒律

史婷婷, 張順利

(西北大學數學學院, 陜西 西安 710127)

1 引言

對稱和守恒律在物理, 數學和其他自然科學領域有著舉足輕重的作用. 無窮多守恒律的存在是證明方程的可積性的強有力證據, 對于一個具有無窮多自由度的非線性系統, 如果它具有無窮多的對稱性和守恒律, 則該系統是在具有無窮多守恒律意義下的可積系統[1-2]. 為了尋求非線性系統的對稱和守恒律, Ibragimov 提出了伴隨方程法[3-5],該方法可以用來尋求任意微分方程的李對稱, Lie-B¨acklund 對稱或留數對稱有關的守恒律, 并得到了廣泛應用[6-11]. 本文首先運用李群分析法求得mBKK 方程組李對稱, 并證明該方程組具有非線性自伴隨性, 最后結合方程組的非線性自伴隨性及求得的李對稱, 運用伴隨方程法構造mBKK 方程組的守恒律.

對于(2+1) 維Broer-Kaup-Kupershmidt 方程組

當y=x時, 可將其化為(1+1) 維BKK 方程組

將上面的方程組改寫為mBKK 方程組

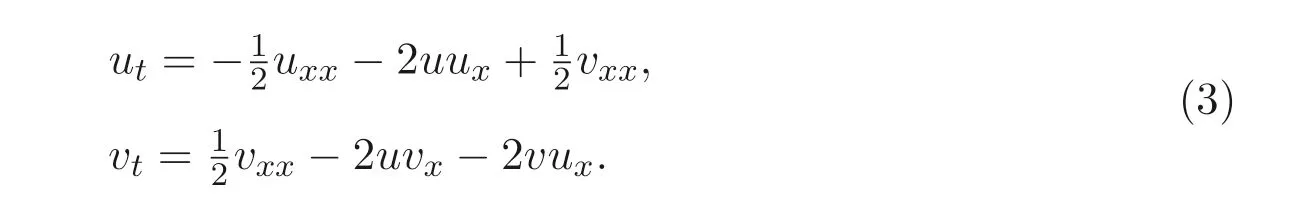
方程組(1) 是描述非線性和色散長重力波在淺海水平方向均勻深度的模型, 它被廣泛應用于等離子體物理、液體力學、非線性光學等各個領域. 文獻[12] 用Hirota 方法把該方程化為雙線性方程, 然后通過攝動法尋找其精確解; 文獻[13] 用李群方法得到該方程的對稱和相似約化, 并借助輔助函數法求解約化方程, 從而得到其部分精確解; 文獻[14] 用修正CK 直接法得到方程的對稱、約化, 再通過求解約化方程得到該方程組的一些精確解. 經查找知, 相關文獻主要針對(2+1) 維Broer-Kaup-Kupershmidt 方程組進行研究, 而對mBKK 方程研究較少. 文獻[15] 用Painlev′e分析法, 證明mBKK 方程具有用Painlev′e 性質, 且在Painlev′e 分析的基礎上通過Schwarz 導數的性質, 求出了方程的精確解. 本文則主要研究mBKK 方程的對稱、自伴隨性及守恒律.

2 mBKK 方程的李對稱分析

mBKK 方程組(3) 可寫為

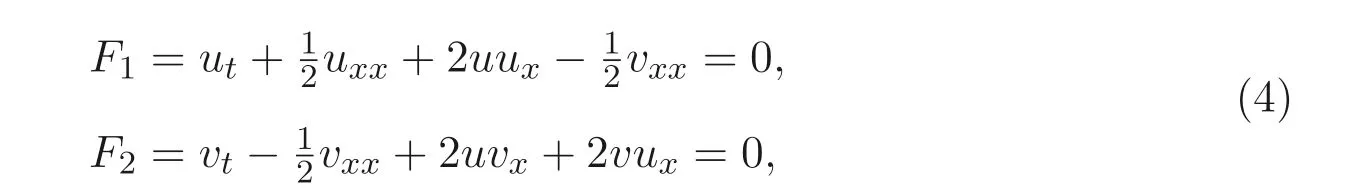
則方程組(4) 的單參數李群的無窮小變換為

這里小參數? ?1, 則變換群(5) 對應的向量場為:

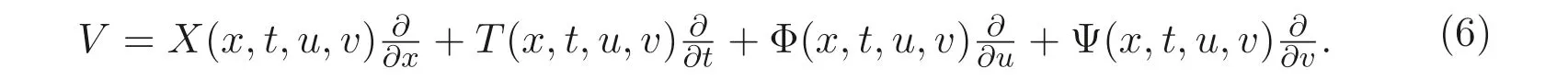
若向量場(6) 是方程組(4) 的李對稱, 則要求方程組(4) 在變換u=u+?σ1,v=v+?σ2下保持形式不變. 這里

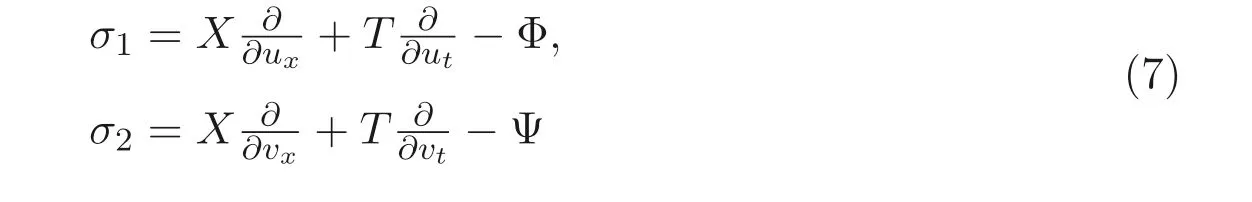
表示u,v的滿足方程的對稱.σ1,σ2滿足方程組(4) 的線性方程組

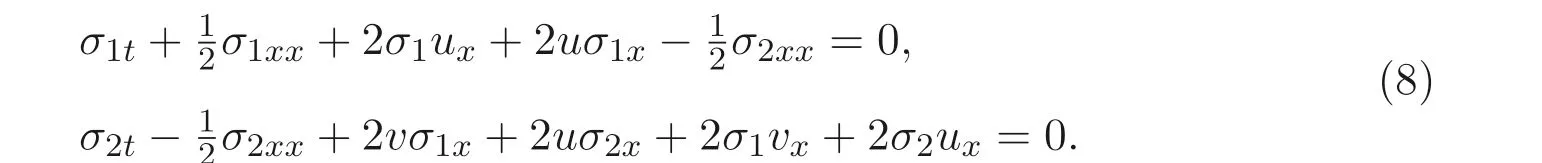
將方程組(7) 帶入方程組(8) 中, 由原方程消去ut,vt, 然后再令u,v的各階導數項系數為零, 即可得到一組關于X,T,Φ,Ψ 的線性方程組, 從而可求得

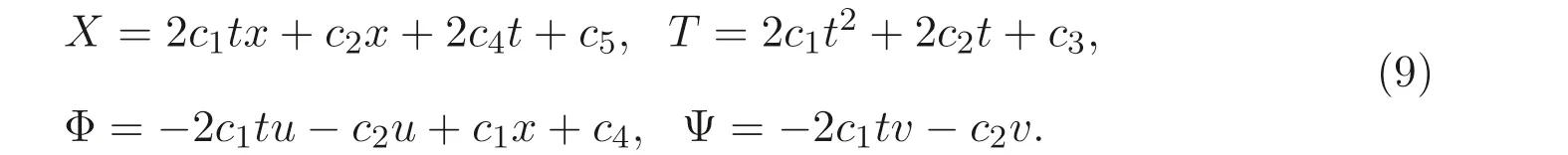
這里c1,c2,c3,c4,c5是任意常數.

基于表達式(9), 由李群分析法可得方程組(4) 的所有向量場

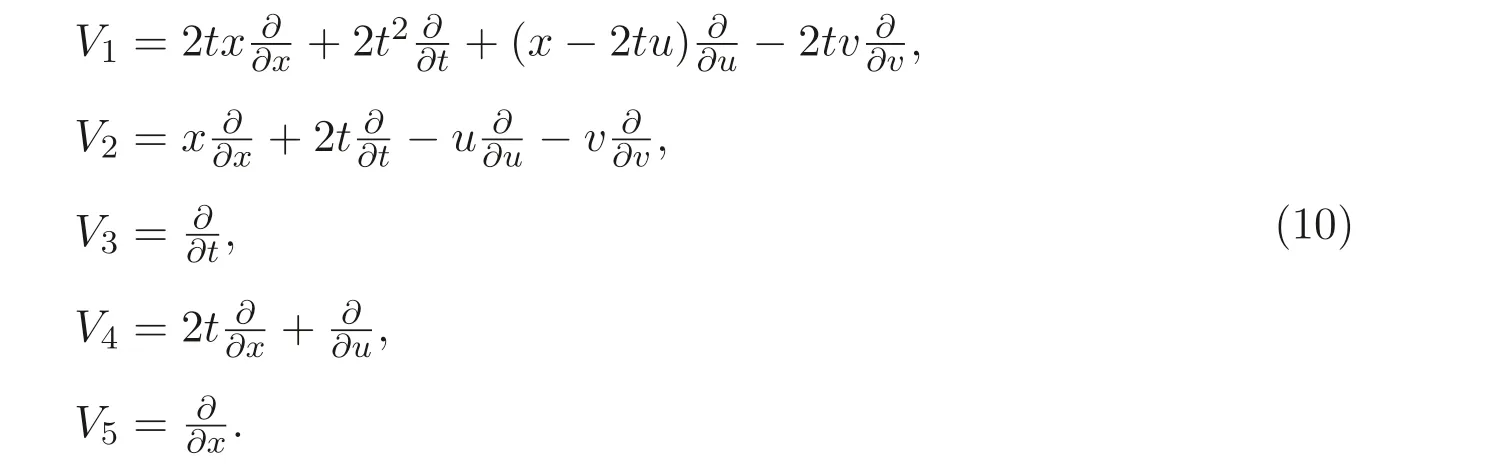
由向量場得方程組(4) 的單參數變換群為

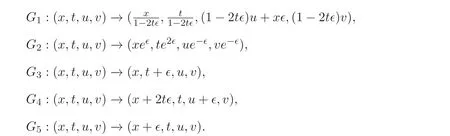
這里?為任意常數. 由于Gi(i=1,2,3,4,5) 為不變群, 故有如下定理. 即

定理2.1[16]如果u=f(x,t),v=g(x,t) 是方程組(4) 的解, 則由Gi確定的方程組(4) 的群不變解為

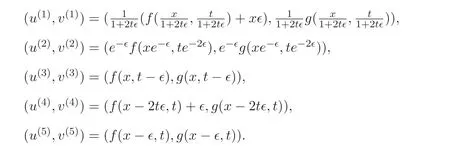
即(u(i),v(i)) 也是方程組(4) 的解.

下面給出向量場(10) 對應的李代數交換子表(見表1).

表1 李代數交換子表

這里[Vi,Vj]=ViVj-VjVi, (i,j=1, 2, 3, 4, 5) 表示的是李代數交換子.

3 mBKK 方程的自伴隨性

定義3.1[5]非線性系統

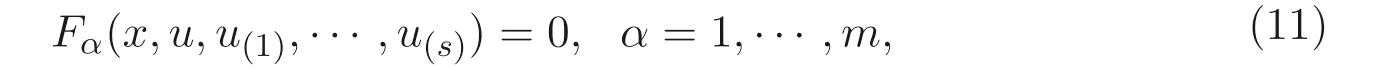
這里x= (x1,··· ,xn),u= (u1,··· ,um),u(s)為u關于自變量的s階偏導數. 則非線性系統(11) 的伴隨系統為

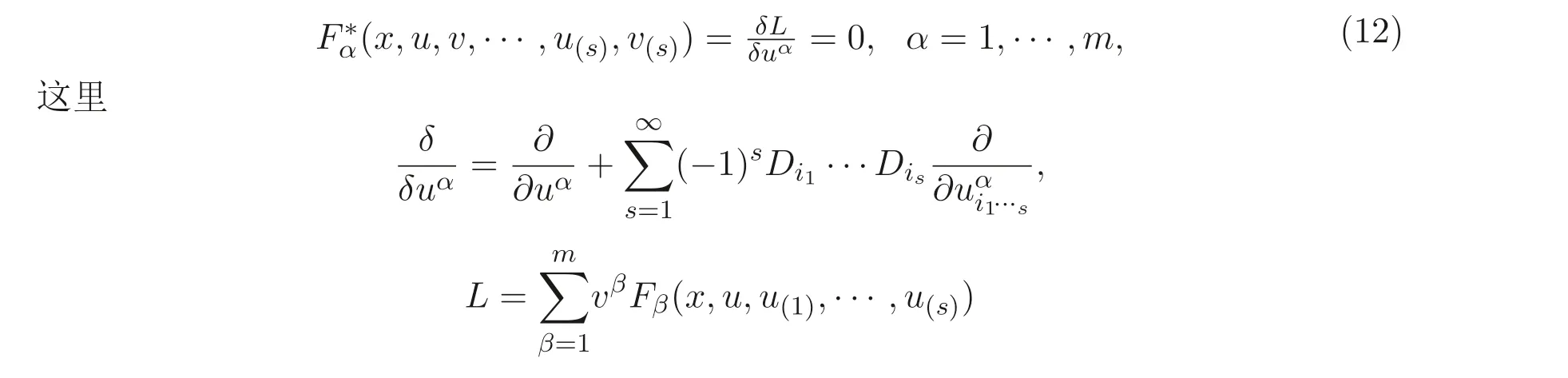
表示的是非線性系統(11) 的標準Lagrangian 函數.

定義3.2[5]非線性系統(11) 具有自伴隨性, 如果它的伴隨系統(12) 在變換vβ=um下等于非線性系統(11).

定義3.3[5]非線性系統(11) 具有非線性自伴隨性, 如果它的伴隨系統(12) 滿足

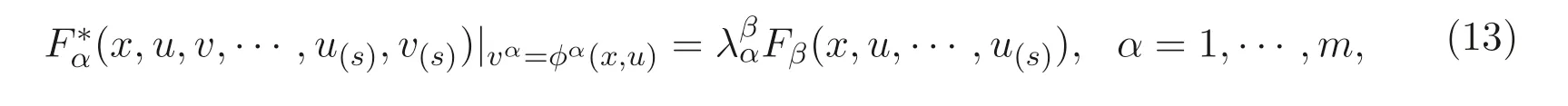
這里u1=u1(x,t),v1=v1(x,t) 為新的因變量.

由定義3.2, 方程組(4) 不具有自伴隨性. 又由定義3.3, 如果能找到

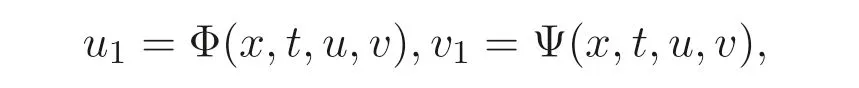
使其滿足方程組(13), 且Φ(x,t,u,v),Ψ(x,t,u,v) 不全為零, 則表示方程組(4) 是具有非線性自伴隨性的. 換句話說, 方程組(4) 是具有非線性自伴隨性的, 如果其伴隨方程組滿足

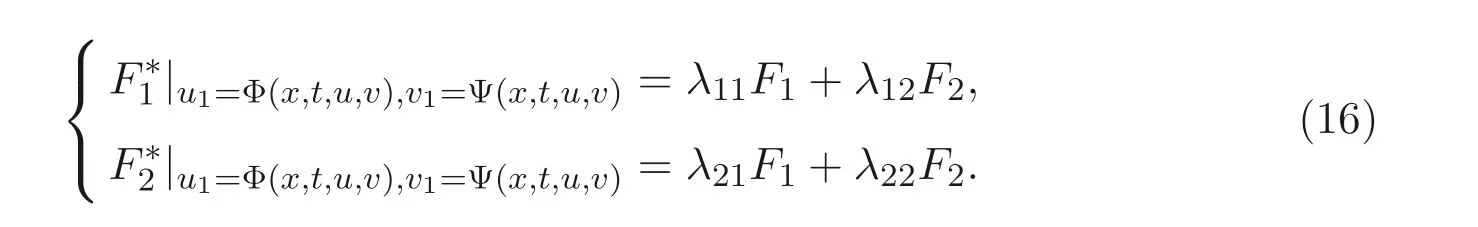
將方程組(4), 方程組(14) 帶入方程組(16), 因Φ,Ψ 不依賴于導數ut,vt,uxx,vxx,···,故方程組(16) 關于系數λij(i,j=1,2) 可分解為如下方程組

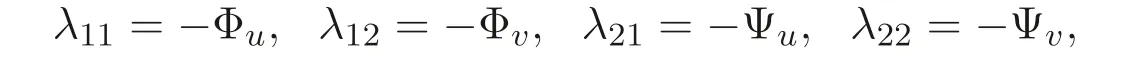
再將上述方程組帶入方程組(16) 中, 得超定方程組

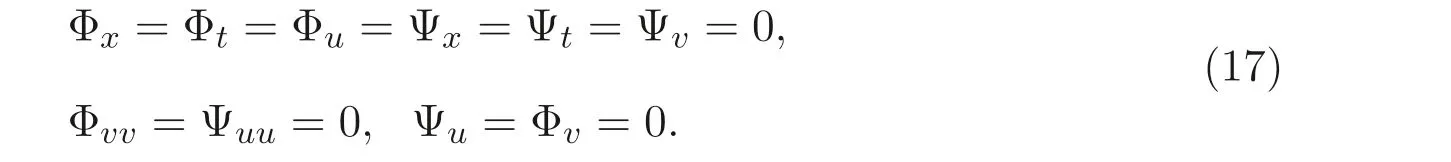
解方程組(17) 可得

這里b1,b2為非零常數. 從而方程組(4) 在變換(18) 下是具有非線性自伴隨性的.

4 mBKK 方程組的守恒律

定理4.1[4]方程組(4) 的任意一個李對稱, Lie-B¨acklund 對稱及留數對稱都可以確定方程組(4) 的一個守恒律, 且其守恒向量場C=(C1,C2) 的表示形式為

這里Wα=ηα ?ξjuαj.

由定理4.1 的結論, 設向量場的通式為

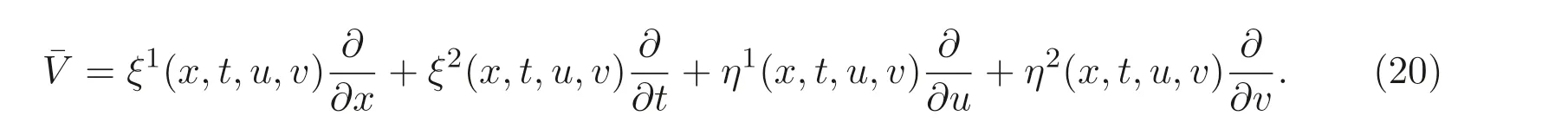
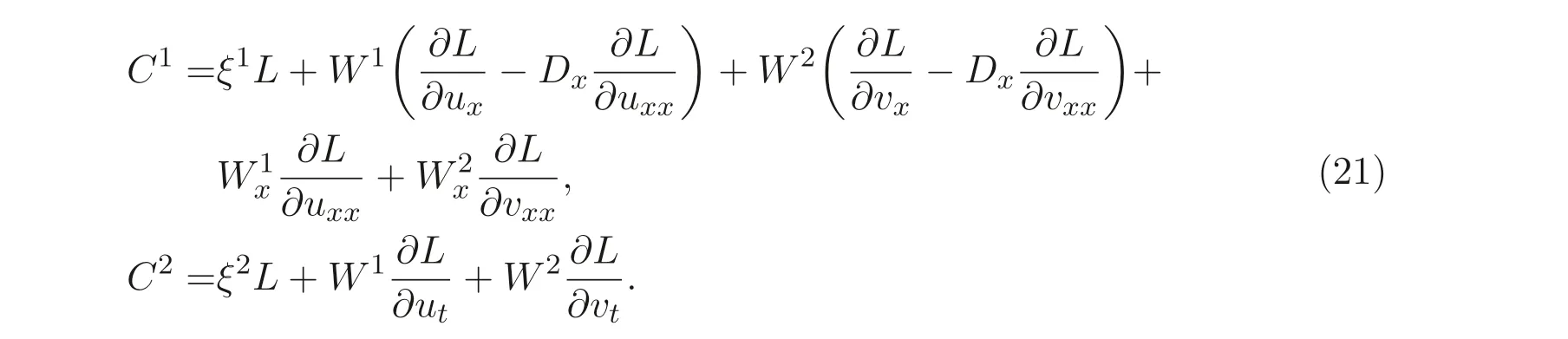
將L帶入(21) 式有

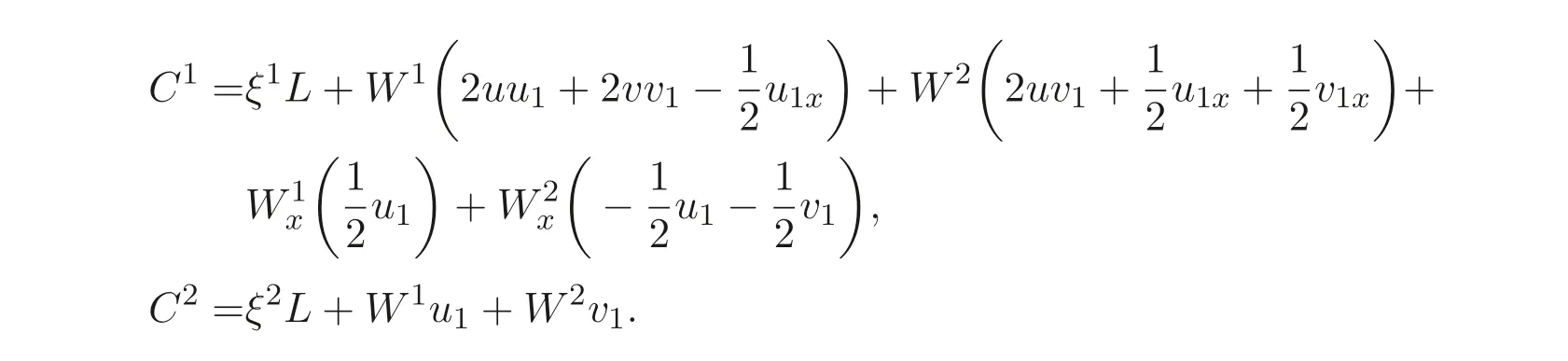
這里W1=η1?ξ1ux ?ξ2ut,W2=η2?ξ1vx ?ξ2vt.

下面分情況討論.

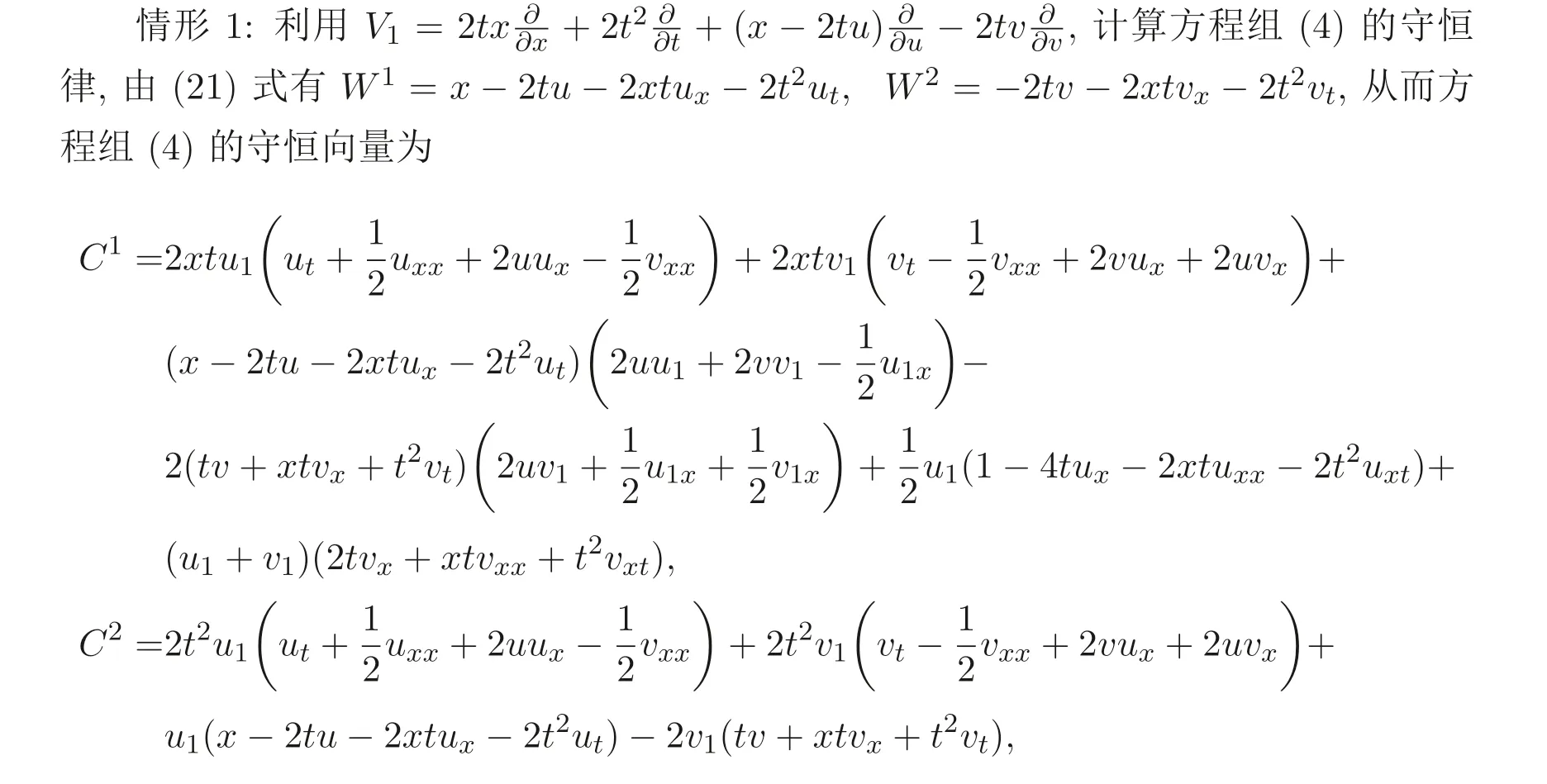
情形2: 利用

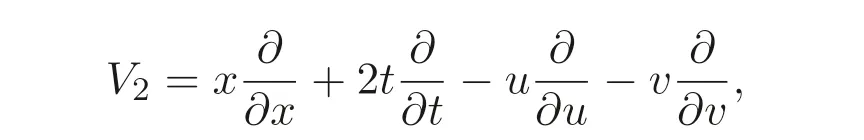
計算方程組(4) 的守恒律, 由(21) 式有

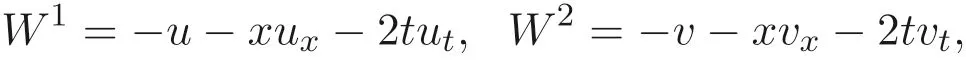
從而方程組(4) 的守恒向量為

通過上面的討論, 發現每一種情況下求出的守恒向量都含有伴隨方程中的任意函數u1,v1, 故給出了方程組(4) 的無窮多守恒律, 同時由符號計算工具Maple 驗證了以上求出的守恒向量滿足守恒律公式Dx(C1)+Dt(C2)=0.

5 結束語

文章證明mBKK 方程組(4) 的非線性自伴隨性, 此性質為后續使用Ibragimov 定理奠定了基礎. 通過對mBKK 方程進行李對稱分析, 得到了其對應的李對稱. 基于方程的對稱性和其對應的伴隨方程, 運用Ibragimov 定理, 構造了方程組(4) 對應的無窮多守恒律, 這對研究微分方程的可積性、線性性和求解方面有著非常重要的作用. 后續研究工作可將伴隨方程的方法推廣應用到其他的非線性偏微分方程的研究.