張拉整體結(jié)構(gòu)模塊組合的力密度法找形與分析

程麗 宋健 張趙威 程欽錕 潘友勝

摘 要：首先在用力密度法對(duì)張拉整體單元找形的基礎(chǔ)上，對(duì)模塊化組合的張拉整體結(jié)構(gòu)進(jìn)行找形分析;其次以三桿張拉整體單元及雙模塊結(jié)構(gòu)為算例，用Matlab工具軟件編程繪出結(jié)構(gòu)的形態(tài)，同時(shí)闡述這種組合結(jié)構(gòu)的形態(tài)特性;最后驗(yàn)證了這種找形可以推廣到任意N模塊，對(duì)實(shí)際工程應(yīng)用具有重要意義。

關(guān)鍵詞：張拉整體結(jié)構(gòu)單元;找形;力密度法;模塊化組合

0 引言

“張拉整體”這一概念最初由美國(guó)學(xué)者Fuller提出[1]，由此概念，張拉整體結(jié)構(gòu)被各國(guó)學(xué)者廣泛研究，并且將張拉整體結(jié)構(gòu)（Tensegrity Structures）定義為：一種處于自平衡狀態(tài)的特殊索桿結(jié)構(gòu)[2]，索桿的組合使結(jié)構(gòu)處于連續(xù)張拉狀態(tài)并保持穩(wěn)定。張拉整體結(jié)構(gòu)最早廣泛應(yīng)用于雕塑作品中[3]，近幾十年逐漸成為國(guó)內(nèi)外熱門話題，學(xué)者們將這種結(jié)構(gòu)與拓?fù)浣Y(jié)構(gòu)聯(lián)系起來，從而把張拉整體思想逐漸應(yīng)用到實(shí)際工程中，涉及航空航天、建筑、生物、智能機(jī)器人等多個(gè)領(lǐng)域。

張拉整體結(jié)構(gòu)的形狀具有多樣性，找形是為了使其幾何形式滿足自應(yīng)力準(zhǔn)則[4]，確定其幾何構(gòu)型及其預(yù)應(yīng)力，來形成一種自平衡且穩(wěn)定的體系，它是張拉整體結(jié)構(gòu)設(shè)計(jì)中的關(guān)鍵。張拉整體結(jié)構(gòu)找形中常見的算法有力密度法、數(shù)值方法[5]、改進(jìn)魚群算法[6]、粒子群算法[7]、遺傳算法[8]等，其中力密度法是一個(gè)被廣泛認(rèn)可的重要找形方法。

通過連接組合張拉整體單元形成的模塊化張拉整體結(jié)構(gòu)是建立模塊化張拉整體結(jié)構(gòu)的主要方法。Snelson在1968年建立了通過沿著軸線連接的張拉整體結(jié)構(gòu)[9];Fuller提出了最初的線型張拉整體結(jié)構(gòu)并構(gòu)造出了理想狀態(tài)的線型張拉整體[10]，所以這種線型的連接是模塊化組合的最普遍方法。

本文以張拉整體單元為研究對(duì)象，用數(shù)值方法求出節(jié)點(diǎn)坐標(biāo)，通過力密度法找到結(jié)構(gòu)的平衡構(gòu)型，以三桿張拉整體結(jié)構(gòu)單元為算例，先對(duì)三桿張拉整體結(jié)構(gòu)找形，再引入重疊率方程對(duì)找形后的單元模型進(jìn)行模塊化組合。利用工具軟件Matlab編程繪出組合后的圖形，并對(duì)最終形成的模塊化結(jié)構(gòu)的特性進(jìn)行分析。

1 張拉整體單元找形

力密度法最早由Linkwitz和Schek于1971年提出[11]，由Vassart和Motro[12]于1999年首次用于張拉整體結(jié)構(gòu)的找形分析;利用力密度法找形時(shí)需要設(shè)定的基本參數(shù)有結(jié)構(gòu)的拓?fù)錁?gòu)型（即求連接矩陣）、邊界約束條件、平衡狀態(tài)內(nèi)力等，計(jì)算結(jié)構(gòu)的力密度和各個(gè)桿件的力密度值，從而確定結(jié)構(gòu)構(gòu)型中的預(yù)應(yīng)力。

1.1? ? 建立結(jié)構(gòu)的拓?fù)錁?gòu)型

張緊結(jié)構(gòu)預(yù)應(yīng)力的穩(wěn)定性取決于連通性，這里用連接矩陣表示其結(jié)構(gòu)構(gòu)型。

張拉整體結(jié)構(gòu)中一個(gè)成員l的兩端節(jié)點(diǎn)由a指向b，在a-b節(jié)點(diǎn)的連通性矩陣Cl可定義如下：

Cl（a，b）=? 1， l的連接起點(diǎn)a，-1，l的連接終點(diǎn)b， 0， 無連接關(guān)系 （1）

基于公式（1），節(jié)點(diǎn)間的連接關(guān)系用連接矩陣表示為：

1.2? ? 以節(jié)點(diǎn)坐標(biāo)建立平衡矩陣

結(jié)構(gòu)中每個(gè)節(jié)點(diǎn)處的平衡方程由力密度和連接到節(jié)點(diǎn)的繩索表示，節(jié)點(diǎn)和連接節(jié)點(diǎn)之間的節(jié)點(diǎn)的坐標(biāo)差與力密度有關(guān)，力密度與外部載荷處于平衡狀態(tài)，結(jié)構(gòu)處于平衡狀態(tài)時(shí)，可以表示為：

Aq=f（3）

式中：A為結(jié)構(gòu)系統(tǒng)中桿的平衡矩陣;q為桿的力密度向量;f為作用在節(jié)點(diǎn)上的外部載荷。

可以構(gòu)造出如下形式平衡矩陣：

A=CTdiag（Cx）CTdiag（Cy）CTdiag（Cz）（4）

1.3? ? 力密度

力密度矩陣表示為：

D=CTdiag（q）C（5）

力密度矩陣D中元素按式（6）可以求出：

D（a，b）=? -qab，? ? 如果a≠l，∑l=a qal， 如果a=l，求和? ? ?0，? ? ?a與l不相連，（6）

1.4? ? 平衡矩陣奇異值分解

將平衡矩陣奇異值分解：

A=M∑NT（7）

其中Mk=[m1? ?m2? ?…? ?mk]是平衡矩陣A分解成的一個(gè)左奇異向量，Ns=[n1? ?n2? ?…? ?ns]是平衡矩陣A分解成的一個(gè)右奇異向量，diag（*）和∑為對(duì)角矩陣。

1.5? ? 數(shù)值算例

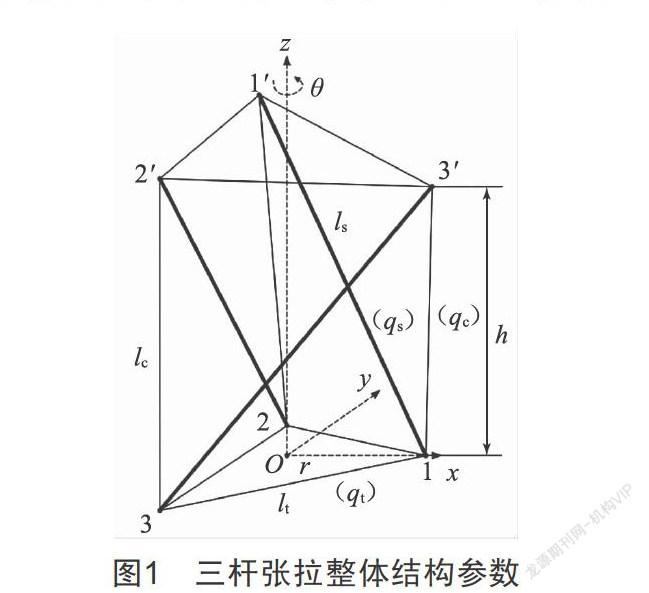
以圖1的三桿張拉整體結(jié)構(gòu)為例：在結(jié)構(gòu)的底面三角形建立笛卡兒坐標(biāo)系，其中上下端面扭轉(zhuǎn)角度θ、桿長(zhǎng)ls、水平索長(zhǎng)lt為已知條件，利用公式（8）（9）（10）求上下端面外接圓半徑r、高度h及最小豎索長(zhǎng)lc，求出節(jié)點(diǎn)坐標(biāo)向量x、y、z。

h2=ls 2-（2r2-2r2cos θ）（9）

lc 2=h2+2r2-2r2cos（-θ）（10）

建立連接矩陣：

C=1? ?-1? ?0? ? 0? ? 0? ?00? ? 1? ?-1? ?0? ? 0? ?01? ? 0? ?-1? ?0? ? 0? ?00? ? 0? ? 0? ? 1? ?-1? 00? ? 0? ? 0? ? 0? ? 1 -10? ? 0? ? 0? ? 1? ? 0 -11? ? 0? ? 0? ? 0? ? 0 -10? ? 1? ? 0? ?-1? ?0? ?00? ?0? ? ?1? ? 0? ?-1? 01? ?0? ? ?0? ?-1? ?0? ?00? ?1? ? ?0? ? 0? ?-1? 00? ?0? ? ?1? ? 0? ? 0 -1（11）