基于改進Johnson-Cook模型的5083P-0鋁合金動態本構關系研究

李恒奎 張光瀚 趙曉春 肖守訥 朱志武

（1 中車青島四方機車車輛股份有限公司，青島 266111）

（2 西南交通大學牽引動力國家重點實驗室，成都 610031）

（3 中國鐵路濟南局集團有限公司青島機車車輛監造項目部，青島 266111）

文 摘 為研究5083P-0 鋁合金在高應變率下的力學行為及本構模型，通過RPL100 材料試驗機和分離式霍普金森壓桿（SHPB），對5083P-0 鋁合金進行了準靜態及應變率范圍950～3 000 s-1的沖擊動態壓縮實驗。結果顯示隨著應變率的增加，5083P-0 鋁合金的屈服強度、流動應力增加，應變硬化率減小，具有應變硬化效應，正應變率效應以及熱軟化效應。對其塑性變形原理進行分析發現，滑移系的作用導致材料發生較大的塑性變形，同時由于絕熱溫升的產生，材料表現出應變硬化與熱軟化機制相競爭的情況。在Johnson-Cook 模型的基礎上對應變率項進行改進，并引入絕熱溫升，改進的Johnson-Cook 模型能夠能較好地描述該材料的應變率效應并能準確地描述其流動應力。最后采用新的應變率進行補充實驗，通過對比驗證了模型的合理性。

0 引言

鋁合金材料因其具有低密度，高強度和高塑性等優良性能而廣泛應用于日常生活、工業生產以及高速列車車體結構中［1-4］。在對鋁合金的使用過程中，不可避免地可能會受到沖擊動態載荷的作用，如車輛碰撞、列車零部件間的撞擊等［5］。經驗表明，沖擊動態載荷條件下與準靜態載荷條件下材料的力學性能會有所不同。鋁合金材料會出現隨著應變率的增大，屈服應力與流動應力提高、應變硬化率降低等現象。因此，對于鋁合金在沖擊動態載荷下的力學性能亟待研究。

隨著沖擊動態力學發展以及實驗設備的革新，國內外學者也更加系統地研究了各牌號鋁合金材料的沖擊動態力學性能。諸多研究表明，鋁合金材料的力學性能會隨著不同的合金成分、含量以及加工硬化、熱處理的不同，而產生不同的力學性能。然而，關于研究5083P-0 鋁合金力學性能的文章甚少，特別是其沖擊動態力學性能的研究。

近年來，由于高鐵迅速發展，鋁合金材料的沖擊動態力學性能逐步得到國內外研究者的廣泛重視，并獲得了較多的成果。目前對于鋁合金動態力學性能的研究往往集中在實驗部分上，通常情況下鋁合金材料具有較弱的應變率敏感性，但一些研究表明鋁或者鋁合金在某些條件下應變率敏感性會增強。對于大部分鋁合金，如7150［6］、3004［7］、6061［8］鋁合金都具有明顯的應變率強化效應，即當溫度一定時，屈服應力和流動應力隨著應變率的增大而明顯增大。還有研究表明不同牌號的鋁合金材料應變率敏感性會有所不同，如7050，2024等鋁合金表現為應變率不敏感［9-10］；而3004、2219等鋁合金表現出應變率敏感性［11-12］。

國外對5083 鋁合金進行了較早的研究［13-14］，國內已對5083 鋁合金的超塑性［15］、高溫本構［16］和中低應變率［17］的力學性能進行了研究。對于5083的本構研究方面，高寧［18］、晏寧［19］等對5083 鋁合金進行了寬應變率下的實驗，通過Johnson-Cook（J-C）模型和Zerilli-Armstrong（Z-A）模型合理描述了5083 鋁合金的拉伸“V”型率效應特征，并引入損傷變量將J-C 模型改進，使模型得以描述5083的軟化效應。

5083P-0 鋁合金的準靜態力學性能可以從材料手冊中獲得，但其沖擊動態力學性能很難獲得。鑒于此，本文通過沖擊動態壓縮實驗獲取5083P-0 鋁合金應力應變曲線，進而揭示該材料在不同應變率加載條件下的沖擊動態力學性能。

1 實驗及原理

5083P-0 鋁合金動態壓縮實驗利用分離式霍普金森壓桿完成，采用圓柱形試樣，尺寸為Φ6 mm×4 mm。實驗原理如圖1所示。

圖1 SHPB設備示意圖Fig.1 Schematic diagram of SHPB equipment

分離式霍普金森壓桿由入射桿、透射桿和吸收桿組成，其中壓縮實驗設備的入射桿直徑14.5 mm、長度400 mm，透射桿直徑14.5 mm、長度為525 mm，最大撞擊速度為60 m/s。此外，還包括超動態應變儀、高速攝像頭以及外部數據采集系統。實驗后將得到的波形采用二波法處理［20］。實驗時，首先調整汽缸的氣壓，子彈受氣缸內的壓力進而發出，通過控制氣壓來控制子彈的速度，進而控制了加載應變率，加載氣壓與子彈射出速度的關系曲線如圖2所示。

圖2 氣壓壓強與子彈速度關系圖Fig.2 Relationship between air pressure and bullet velocity

由一維應力波理論并引入均勻性假設［21］，得到材料的應變率(t)、應變ε(t)和應力σ(t)：

式中，ls、As分別為試樣的長度和橫截面積，A、E分別為壓桿的橫截面積、彈性模量，ρ為壓桿的密度，εi為入射應變波、εr為反射應變波、εt為輸出桿上的透射應變波，C0為應力波在桿中的傳播速度。

由此得到試樣的應力、應變、應變率與時間的關系，進而得到應力、應變、應變率三者之間的相互關系。

2 實驗過程及結果

沖擊動態壓縮實驗加載應變率分別為：950、1 500、2 000、3 000 s-1，在每個加載應變率下進行兩次重復實驗，若一致性不好，再進行第三次實驗。壓縮應力應變曲線及塑性段應力應變曲線如圖3、圖4所示。

圖3 沖擊壓縮加載下的應力應變曲線Fig.3 Stress strain curves under impact compression loading

圖4 沖擊壓縮加載下塑性段的應力應變曲線Fig.4 Stress strain curves of plastic section under impact compression loading

由圖3、圖4可以看出，在沖擊動態下5083P-0鋁合金不同應變率的應力應變曲線在彈性階段基本重合，而屈服應力隨著應變率的增加有一個明顯的提升，而在塑性階段，隨著應變率的升高流動應力明顯升高。說明在高應變率下5083P-0 鋁合金表現出明顯的應變率效應。與此同時，隨著應變不斷增加應力也在不斷增加，該材料在動態壓縮加載下表現出明顯的應變硬化效應，塑性變形所示的屈服強度的應變速率依賴性可以通過熱激活位錯理論來解釋。曲線后半段出現應變軟化現象，是由于高速沖擊會使材料內部產生絕熱溫升，導致材料出現應變軟化現象，該段曲線表現出應變硬化與熱軟化機制相競爭的情況。

為了更好地說明5083P-0鋁合金的力學性能，根據GB/T7314—2005要求［22］，準靜態壓縮實驗采用圓柱形試樣，尺寸為Φ6 mm×4 mm。采用RPL100材料試驗機完成5083P-0鋁合金的準靜態壓縮實驗，加載應變率為0.01 s-1。將準靜態曲線與動態曲線進行對比，如圖5所示。

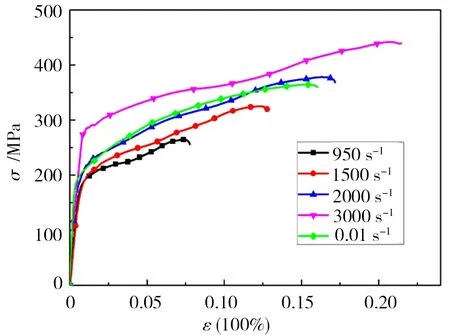
圖5 5083P-0鋁合金準靜態與動態實驗曲線對比Fig.5 Comparison of quasi-static and dynamic experimental curves of 5083P-0 aluminum alloy

可以看出在應變率低于2 000 s-1時，材料的動態屈服強度明顯低于材料靜屈服強度。根據晏寧、高寧的研究［11-12］可知，對于5083鋁合金當應變率小于10 s-1時，材料表現出負應變率效應，屈服應力隨應變率變大而變小；當應變率大于10 s-1時，材料表現為正應變率效應，屈服應力隨應變率變大而變大。因此當材料處于低應變率時的屈服強度反而高于950 s-1、1 500 s-1應變率下的屈服強度。說明無論是準靜態還是動態壓縮下5083P-0鋁合金都有很大的塑性變形。對于大部分金屬而言，發生塑性變形主要由孿生和滑移共同作用，由于鋁合金為面心立方晶體，其發生孿生時所需的臨界分解剪切應力比滑移大，一般情況可以忽略孿生對其塑性變形的影響。因此5083P-0鋁合金塑性變形機理主要是晶粒的滑移，在沖擊荷載作用下，試樣內部晶粒發生滑移、變形。隨著參加滑移的晶粒越來越多，起作用的滑移系也越來越多，最終擴散到試樣內部的全部滑移系，試樣發生較大的塑性變形。

3 Johnson-Cook本構模型

就沖擊動力學而言，模擬材料力學響應的本構方程是否標準將嚴重影響到分析結果的準確性。Zerilli-Armstrong（Z-A）和Johnson-Cook（J-C）模型的推導都是基于經驗和半經驗模型，它們所涉及的材料常數比物理模型更少，并且只需要有限的材料試驗數據，因此可以更有效地用來預測材料的力學性能。目前Johnson-Cook模型是經驗模型中使用最廣泛的模型之一［23-30］，其包括5個材料常數，其中應變率硬化項和溫度軟化項是最為重要的部分。為了提高Johnson-Cook模型的準確性，本文對模型進行了一些修改，結合Johnson-Cook應變率強化項和溫度項改進，為高強度合金材料的流動應力提供精確的估計。

Johnson-Cook模型應力應變關系可表示為［31］：

式中，(A+Bεnp)、(1+Cln)、(1-T*m)分別為描述材料加工硬化效應、應變率效應和溫度軟化效應。其中σ為Von-Mises流動應力。A為參考應變率和參考溫度下的屈服強度，B、n分別為材料硬化模量和硬化指數，C為材料應變率敏感（強化）系數，m為材料溫度軟化指數，各參數均由實驗獲得。εp為等效塑性應變，為無量綱等效塑性應變率，為參考應變率。為無量綱化的溫度項，Tm、Tr分別為材料的熔點溫度（730 ℃）和室溫（20 ℃），A在此參考溫度下測定。

根據前文中的實驗數據來擬合Johnson-Cook 本構方程的各參數。

3.1 確定參數A、B和n

式（4）右邊第一個括號項表示T=Tr及=時的σ-ε關系。參數A為材料在參考應變率下的屈服強度，通常將準靜態實驗的應變率定為參考應變率，即A為準靜態實驗條件下的屈服強度。但是由于5083P-0存在負應變率效應，若取準靜態實驗的屈服強度作為參數A的值，會導致動態屈服強度低于準靜態屈服強度的曲線無法擬合。根據晏寧的研究［12］5083鋁合金在低應變率到中應變率過程中存在負應變率效應，材料的屈服強度逐漸降低，在應變率為10 s-1時到達最小，為149 MPa。而在中應變率到高應變率的過程中，存在正應變率效應，材料的動態屈服強度逐漸提高。因此在試樣的初始溫度條件下，即T=20 ℃時，選取應變率=10 s-1為參考應變率，根據參考應變率下實驗測量所得σ-ε曲線即可確定A、B和n。此時，式（4）可化簡為：

首先可以確定A，即材料參考應變率下的屈服應力為149 MPa。

其次確定B和n，將式（5）兩邊同時取對數，并帶入A可以得到關系式：

做出ln(σ-A)-lnε曲線，曲線的截距為lnB，斜率為n(tanα)，于是可以得到B和n的值。

3.2 參數C的確定

從J-C模型中可以看出當塑性應變零，且實驗處于室溫條件下時，此時的應力為動態屈服應力，J-C模型變成：

常溫下5083P-0 鋁合金的屈服應力與應變率的關系做出了σy-ln圖，如圖6所示，根據求解n的過程，利用式（7）便可擬合出參數C。

圖6 Johnson-Cook本構模型參數C的擬合Fig.6 Fitting parameter C of Johnson-Cook constitutive model

通過準靜態常溫高溫實驗，沖擊動態實驗，得到參數如表1所示。

表1 J-C本構方程參數Tab.1 Parameters of J-C constitutive equation

將兩組參數值代入式（4）中，得到5083P-0 鋁合金的Johnson-Cook本構方程為：

3.3 改進的Johnson-Cook本構模型

由圖6不難發現，σy與ln之間并不是完全的線性關系，高應變率下強化效應更加顯著，單純用線性變化關系來描述并不合適，因此對模型中的應變率強化項作適當修正。假設兩者存在指數對應關系，如公式（9）所示，對J-C模型進行改進，并對實驗點進行擬合，見圖7。

圖7 σy與ln ε*擬合關系Fig.7 The fitting relationship between σy and ln ε*

可以看出，該指數能更好的描述σy與ln的關系，因此將J-C 模型的應變率項進行改進，得到改進后的J-C模型：

模型中各參數值見表2。

表2 改進后J-C模型各參數值Tab.2 Parameters of improved J-C model

由式（10）可以看出模型并沒有考慮高應變下材料絕熱溫升的因素。在高速沖擊條件下，由于變形速度過快，能量迅速增加，由此產生的熱量無法在短時間內向外界傳遞，此過程可視為絕熱條件。而該溫度為材料內部溫度，溫度的測量是實驗的難點所在。根據文獻［33-34］對于高應變率下材料絕熱溫升的研究，如果材料變形是在等溫環境有熱交換的情況下進行的，則流動應力將高于沒有絕熱的情況。通過間接方法，可以確定變形過程中材料內部溫升，即在實驗后用量熱法測量儲存的能量：

式中，ΔW為所做的功，ΔQ為產生的熱量，η為塑性功熱轉換系數，σe為真實應力，ε為真實應變，Cu為室溫比熱，ρ為材料密度，ΔT為絕熱溫升。

將5083P-0 鋁合金的密度2.70 g/cm3、室溫比0.9（J/kg·℃）、塑性功熱轉換系數0.9 代入式（13）并結合實驗曲線計算可得到各加載應變率下的絕熱溫升，如表3所示。各加載應變率下實驗與理論對比圖見圖8。

表3 各加載應變率對應的絕熱溫升Tab.3 Adiabatic temperature rise corresponding to each loading strain rate

將J-C在考慮絕熱溫升后再次改進：

分析圖8中四種加載應變率的對比結果可以得出：改進J-C模型的理論與實驗曲線擬合良好，反映了應變率效應和絕熱溫升軟化效應對5083P-0鋁合金動態壓縮過程中流動應力影響趨勢，改進J-C模型可較好地描述5083P-0鋁合金的動態壓縮力學性能。具體表現為：改進J-C模型能更準確地描述各應變率條件下的材料屈服點以及各應變率下的應變率強化效應，同時該模型可以表述材料熱軟化效應，很好地反映高應變率下應變硬化與熱軟化機制相競爭的情況。

4 模型的合理性驗證

為了驗證模型的合理性與應用性，進行一次補充實驗，采取與前文不同的應變率進行實驗。得到塑性段的應力應變圖，如圖9所示。

圖9 1 300 s-1應變率下的5083P-0壓縮應力-應變曲線Fig.9 5083P-0 compressive stress-strain curve at 1 300 s-1 strain rate

將1 300 s-1的應變率代入到式（14），得到1 300 s-1應變率下的5083P-0 的本構方程理論曲線，將實驗與理論曲線進行對比，如圖10所示。

圖10 1 300 s-1應變率下的壓縮實驗曲線與理論曲線對比圖Fig.10 Comparison of compression experimental curve and theoretical curve at 1 300 s-1 strain rate

從圖10看到，在新的應變率下該模型也能對實驗曲線進行很好的擬合與描述，說明改進后的J-C模型可以對不同工況下的5083P-0 鋁合金進行預測與描述，驗證了模型的合理性與應用性。

5 結論

對5083P-0 鋁合金進行了沖擊動態加載實驗，得到其不同應變率下的應力-應變曲線。通過對J-C模型改進，得到了更加適用于5083P-0 鋁合金的沖擊動態本構模型。相關的研究結論如下：

（1）通過5083P-0 鋁合金在準靜態和沖擊動態加載下的壓縮實驗可以看出，流動應力隨著應變的增加而明顯增加，5083P-0鋁合金具有明顯的應變硬化現象；在沖擊壓縮實驗中隨著應變率的增加，5083P-0鋁合金的屈服應力及流動應力逐漸增加，說明沖擊壓縮時具有應變率效應；

（2）5083P-0鋁合金沖擊動態加載下曲線后半段出現應變軟化現象，是由于高速沖擊會使材料內部產生絕熱溫升，導致材料出現應變軟化現象，該段曲線表現出應變硬化與熱軟化機制相競爭的情況；

（3）通過對材料屈服應力與應變率的研究，改進J-C 模型中的應變率項，并引入絕熱溫升對溫度項進行改進，使得該模型可以在沖擊加載條件下對各應變率范圍都能進行很好的擬合。最后添加新的應變率進行補充實驗和合理性驗證，通過理論和實驗曲線的對比，驗證了模型的合理性。