基于稀疏貝葉斯學習在未知噪聲場的欠定寬帶信號DOA估計

郭業才， 田佳佳， 胡國樂

（1.南京信息工程大學電子與信息工程學院，南京210044；2.江蘇省大氣環境與裝備技術協同創新中心，南京210044；3.安徽大學電氣工程與自動化學院，合肥230039）

0 引 言

利用傳感器陣列估計寬帶波達方向（Direction of Arrival，DOA）是一個活躍的研究課題［1］，因為它具有廣泛的應用，需要估計所謂的角譜。例如：在雷達、聲吶、無線通信和定位等。由于DOA估計準確度是由傳感器陣列的自由度（Degree of Freedom，DOF）決定的，均勻間隔陣列需要增加傳感器數量才能獲得較高的DOF，而提高了制造成本和陣列標定的難度。稀疏陣列，即嵌套陣列和互質陣列［2-3］，可以獲得更高的DOF數目，比使用非均勻傳感器位置的物理傳感器數目解析更多的源。對于稀疏陣列，利用擴展協方差矩陣實現DOF的增加，其虛擬傳感器位置由物理傳感器之間的連續和非連續滯后差決定。

在稀疏陣列中，互質陣列由于其簡單的陣列結構和檢測比物理傳感器數量更多的信號的能力，引起了人們對DOA估計應用的極大興趣［4］。利用多個頻率來填充缺失的共線陣元，互質陣列可以有效地獲得所有提供的DOF，用于高分辨率DOA估計［5］。利用陣列信號模型的稀疏性，稀疏信號表示技術促進了DOA估計的進展［6］。這些基于稀疏信號表示的算法不僅將感興趣的范圍離散為空間角網格，而且假設真實信號DOA必須落在預定義的網格上。然而，在實際情況中，無論網格有多密集，真正的DOA不一定位于準確的采樣網格上。這種離網源會導致字典失配問題，不僅違反稀疏性條件，而且會降低性能［7］。Shen等［8］提出了一種基于組稀疏的兩步離網源欠定寬帶DOA估計方法，該方法比現有的基于組稀疏的同網格搜索方法具有更好的性能。為解決聯合稀疏性無法捕獲信號真實結構的問題，提出一種稀疏貝葉斯框架內的寬帶DOA估計算法，可以更靈活地占用頻譜帶，并通過在潛在參數空間上施加Dirichlet過程來自動確定潛在的波段占用［9］。

稀疏貝葉斯學習（Sparse Bayesian Learning，SBL）作為一種壓縮感知（Compression Sensing，CS）實現，彌補了在聯合處理多個頻率和多個快照以定位一個或多個源時，多個稀疏解可能對應于一個源的缺點［10-11］。作為一種概率方法，SBL計算稀疏權向量的后驗分布，并給出其協方差和平均值［12］。將SBL思想應用于稀疏信號恢復的單測量向量（Single Measurement Vectors，SMV）模型中，通過貝葉斯規則得到后驗概率p（x｜y；Θ），Θ為所有超參數［13-14］。超參數是通過在x上進行邊緣化，執行證據最大化或ii型最大似然來從數據中估計的［15］。SBL的魅力在于它的全局極小值總是最稀少的一個［16］，而流行的l1-norm優化算法并不是全局收斂［17］。因此，基于SBL的優化算法明顯優于傳統的l1-norm優化算法。

本文研究了基于互質陣列的SBL算法在未知噪聲場中對離網源的欠定寬帶DOA估計。互質陣列采用最小稀疏標尺重構空間協方差矩陣，用非均勻采樣方法，提倡采集少量樣本，避免寬帶信號的混疊。將協方差矩陣向量化，利用克羅內克積從互質陣列得到虛擬流形矩陣，利用SBL算法得到寬帶信號的DOA估計。在稀疏貝葉斯框架下開發的SBL算法可以近似地解決非凸優化問題，并利用定點更新自動確定稀疏性。基于SBL的寬帶DOA估計方案在采集少量樣本的情況下，尤其在低信噪比（Signal-to-Noise Ratio，SNR）的情況下，可以提供處理優勢。

1 互質陣列的寬帶信號模型

一個互質陣列，它包括2個帶有N和2M傳感器的均勻線性陣列（Uniform Linear Array，ULA），如圖1所示。圖中，第1、第2個子陣列的元素間距分別為Mλ/2和Nλ/2。λ為信號的中心波長。假設遠場K個寬帶信源sk（t），k＝1，2，…，K以入射角Θ＝［θ1，θ2，…，θK］射在互質陣列上。在互質陣列的第w個傳感器處觀察到的信號可以表示為式中：0≤w≤2M＋N－1；sk（t）為第k個信號；nw（t）為未知噪聲信號；τw（θk）為第k個入射信號以入射角θk

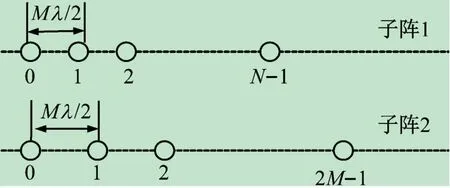
圖1 互質陣列模型

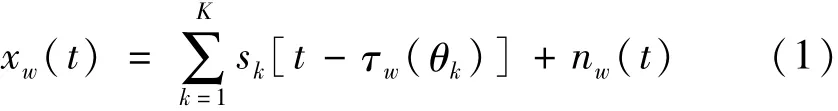
到達互質陣列的第w個傳感器的時間延遲。對觀察到的傳感器信號作L點離散傅立葉變換（Discrete

Fourier Transform，DFT），在頻域中，在第w個傳感器處接收的數據向量可以表示為

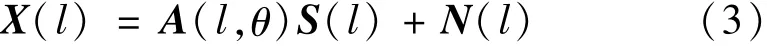
式中：A（l，θ）＝［a（l，θ1），a（l，θ2），…，a（l，θK）］為方向矩陣；a（l，θK）為對應入射角的導向向量。

數據向量的協方差矩陣為

式中：E｛·｝為期望運算符；｛·｝H為厄米轉置運算符為第k個信源的方為相應的噪聲方差；a（l，θk）為導向向量。在實際情況下，理論協方差矩陣Rl是不可能得到的，可以使用T個可用段（頻率快照）估算樣本協方差矩陣：

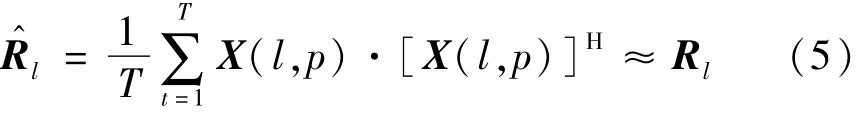
信號協方差矩陣Rl向量化為

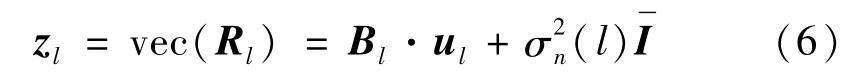
式中：Bl＝［b（l，θ1），b（l，θ2），…，b（l，θK）］為等效導向向量構成的矩陣；b（l，θk）＝a*（l，θk）?a（l，θk）為等效導向向量；入射信號方差矩陣和單位矩陣轉化后的列向量vec（I）。其中符號‘*’為復共軛；符號‘?’為克羅內克積（前一個矩陣中的每一個元素都與后一個矩陣相乘）；vec（·）為將矩陣轉化為列向量的操作［18］。

來自矩陣Bl的傳感器的位置（被視為較大的虛擬陣列的流形矩陣）在自差分集中

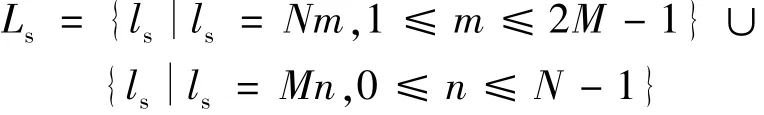
2 帶有離網源的稀疏貝葉斯學習

2.1 離網公式

假設存在以lq（q＝1，2，…，Q）為索引的Q≤L個DFT頻點。那么對應于Q個頻率點的流行矩陣Bl＝［Bl1，Bl2，…，BlQ］。使用固定間隔≤D）的D元素網格θg采樣潛在空間域，g為網格，并將網格間隔離散，則式（6）可以寫成

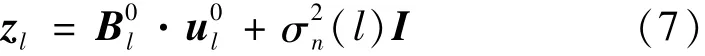
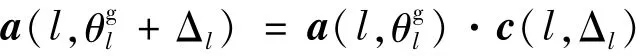
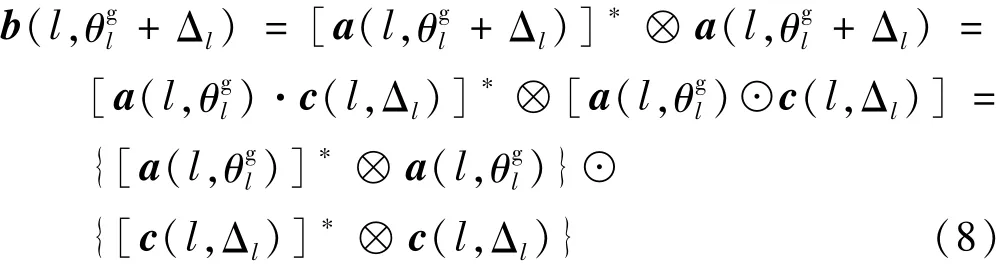
將D個導向向量的集合表示為離網目標下寬帶信號的稀疏表示為

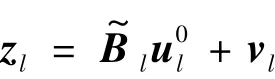
式中，vl為向量，是噪聲部分的集合，除第k個條目（對應于nw（t）的第k個元素的方差）外，它由所有零組成。

可見，噪聲部分vl可以通過每2個不同的zl之間的計算消除，即式中，m＝1，2，…，h，其中h＝L（L－1）/2。

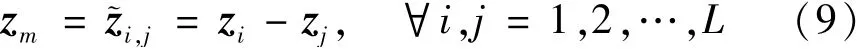
2.2 稀疏貝葉斯學習算法

由于未知噪聲通過式（9）得到消除，因此似然概率為

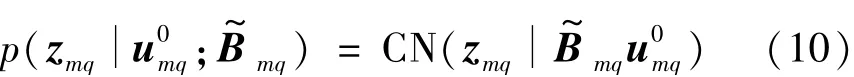
式中：zmq為m點離散傅里葉變換的第q個頻點的寬帶信號稀疏表示；CN為復高斯分布為m點離散傅里葉變換的第q個頻點導向向量的集為m點離散傅里葉變換的第q個頻點的方差的稀疏向量。由于為正實數，因此式（10）可以轉換為以下實值似然概率為

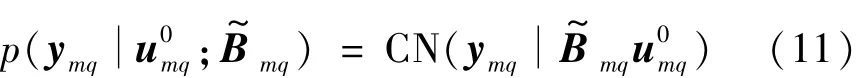
式中：γmq為m點離散傅里葉變換的第q個頻點的源方差；Γmq＝diag（γmq，1，γmq，2，…，γmq，D）＝diag（γmq）為在每個范圍深度單元θ中以γmq作為源方差的對角協方差；γmq，d為在第d個網格處的源方差。

令Ymq＝｛y1q，y2q，…，yhq｝為T個快拍的集合，而源方差向量的相應集合為使用式（11），多重快照似然概率為

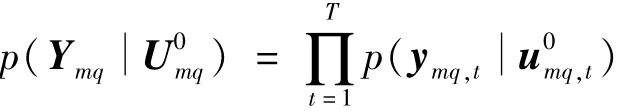
多頻似然概率為

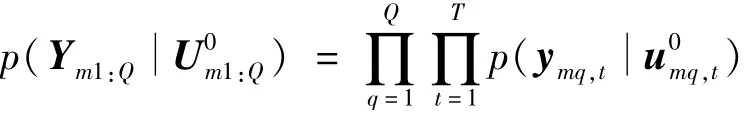
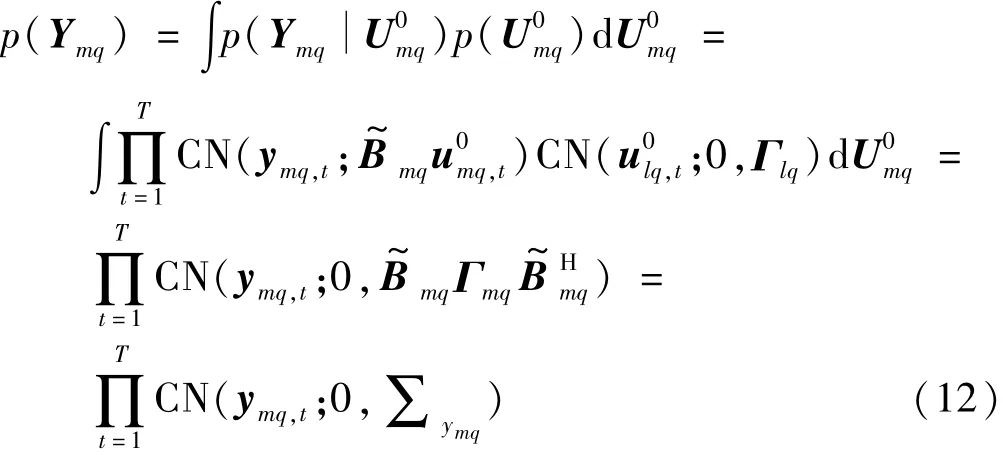
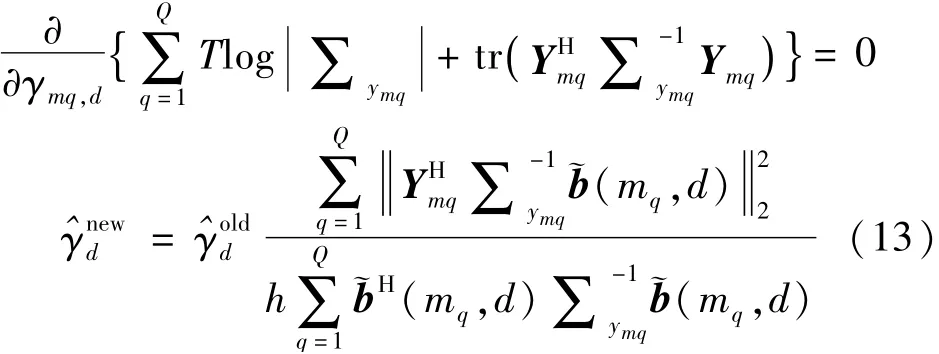
簡而言之，SBL算法可以總結如下步驟：

步驟1初始化＝1。

步驟2輸入

步驟3通過式（13）更

步驟4如，停止。

步驟5和Nt＝Nt＋1。

步驟6如果Nt＜1 000，返回步驟2；否則停止。

3 仿真結果

在本節中，將通過仿真來說明用于寬帶DOA估計的帶互質陣列的SBL算法的性能，并將其與其他最新算法進行比較，包括同時正交匹配跟蹤最小二乘（Simultaneous Orthogonal Matching Pursuit Least

Squares，SOMP-LS）、同時正交匹配跟蹤總最小二乘（Simultaneous Orthogonal Matching Pursuit Total Least Squares，SOMP-TLS）［21］和離網稀疏貝葉斯推理（Offgrid Sparse Bayesian Inference，OGSBI）［22］。在仿真中，信號的分數帶寬（即帶寬與中心頻率的比值）。采樣頻率是最高頻率的3倍。換言之，信號具有從的歸一化頻率范圍，其中歸一化頻率，其中f是感興趣的頻率。考慮在每個頻率點的信號共享相同的分布，即，振幅是瑞利隨機變量，并且相位均勻地分布在［－π，π］上。應用L＝128點DFT，感興趣的頻帶覆蓋Q＝26個頻點。假設有一個K＝12信源的示例，它們的離網沖擊角均勻地分布在之間。互質陣列由M＝3和N＝4的一對稀疏線性陣列（ULA）組成，一共有9個物理傳感器，其位置設置為S＝［0，3，4，6，8，9，12，16，20］λ/2。

比較SBL與SOMP_LS、SOMP_TLS和OGSBI在互質陣列中對欠定寬帶DOA估計的檢測性能。在整個感興趣的頻帶內，信號功率和噪聲功率用來計算信噪比SNR。假設K＝12個寬帶信源入射到M＝3、N＝4的互質陣列上，快拍數為100，輸入信噪比SNR固定為0 dB。如圖2所示，SBL與SOMP_LS、SOMP_TLS和OGSBI可以成功的區分出所有的寬帶信號（信源數超過物理傳感器的數量）。如圖2（a）所示，即使SBL在0rad處也存在一個偽峰，而圖2（b）、（c）中SOMP_LS和SOMP_TLS沒有生成偽峰。如圖2（d）所示，OGSBI會生成一些明顯的虛假峰。與SBL相比，在某些角度上，SOMP-TLS提供了更接近真實值的DOA估計，而對于其他角度，SBL則提供了更好的準確度。因此，使用SBL和SOMP-TLS算法的估計性能是可比的，并且在其他算法中可提供最佳檢測。

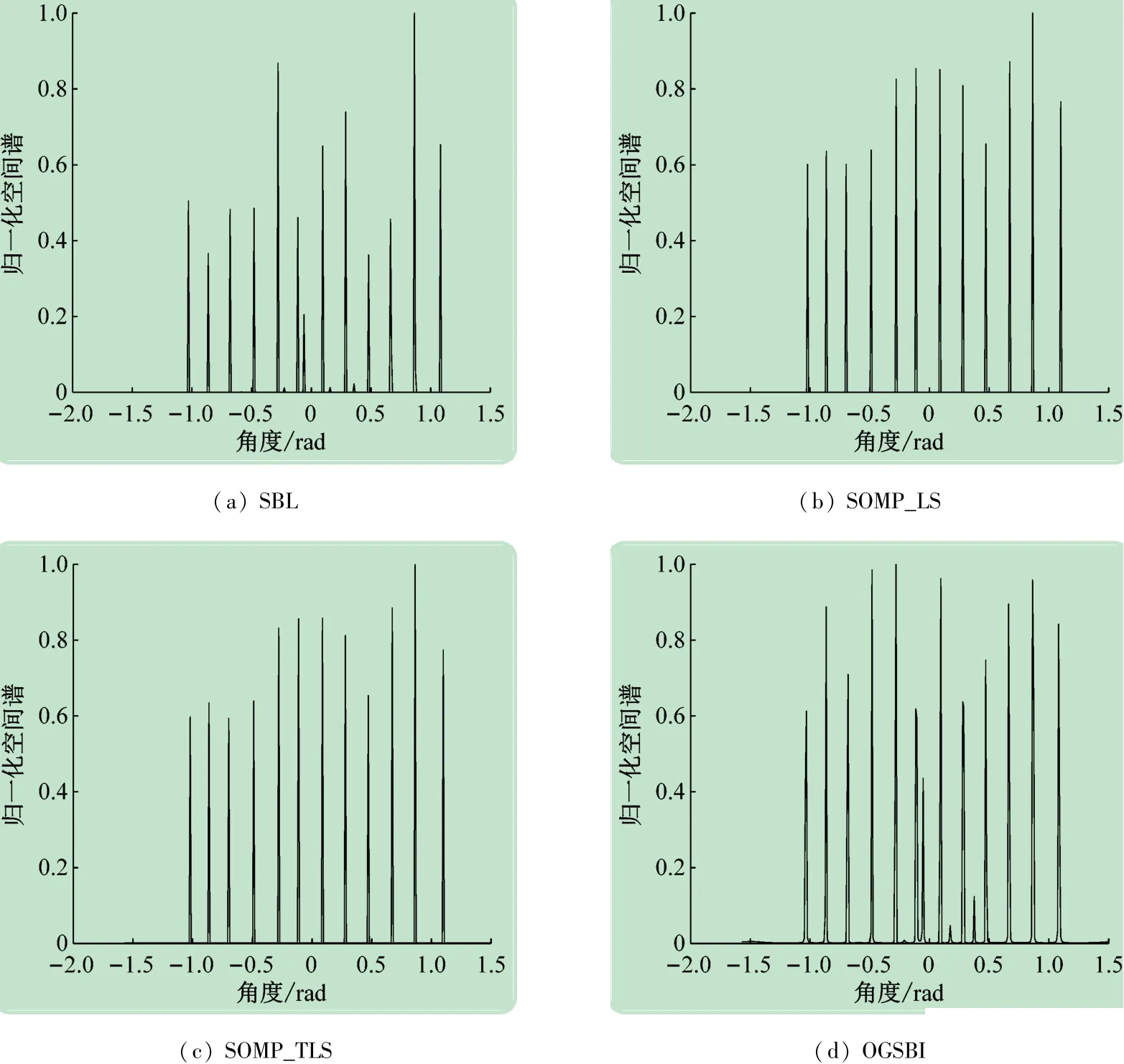
圖2 4種算法在快拍數為100，SNR＝0 dB時DOA估計的歸一化空間譜

為更加具體地觀察出4種算法在互質陣列上對寬帶信號的檢測性能，表1列出了4種算法的檢測結果和待估計DOA。表1表明，SBL算法在絕大多數待估計角度檢測中的表現出優于其他3種算法的性能，檢測結果的誤差均小于其他3種算法。根據均方根誤差（Root Mean Square Error，RMSE）將SBL算法與SOMP_LS，SOMP_TLS和OGSBI算法進行比較，以評估算法的估計精度。用RMSE作為DOA性能評估指標，且

表1 4種算法在SNR＝0 dB，快拍數為100時的角度估計

式中：W為獨立的蒙特卡洛試驗的數為第i個蒙特卡洛試驗的θk的估計值。這里，每個測試點均采用200次蒙特卡洛模擬迭代的平均結果。Crame-Rao下界（CRLB）［23-24］（它提供了估計準確性方差的下界）也用于表示理想估計。

如圖3所示，在快拍數為200時，4種算法隨信噪比的變化，SBL算法的仿真結果表現出比其他3種算法更好的估計性能，尤其是在低信噪比時，SBL算法的RMSE明顯小于其他3種算法，在寬帶信號的DOA估計上表現出更好的性能。

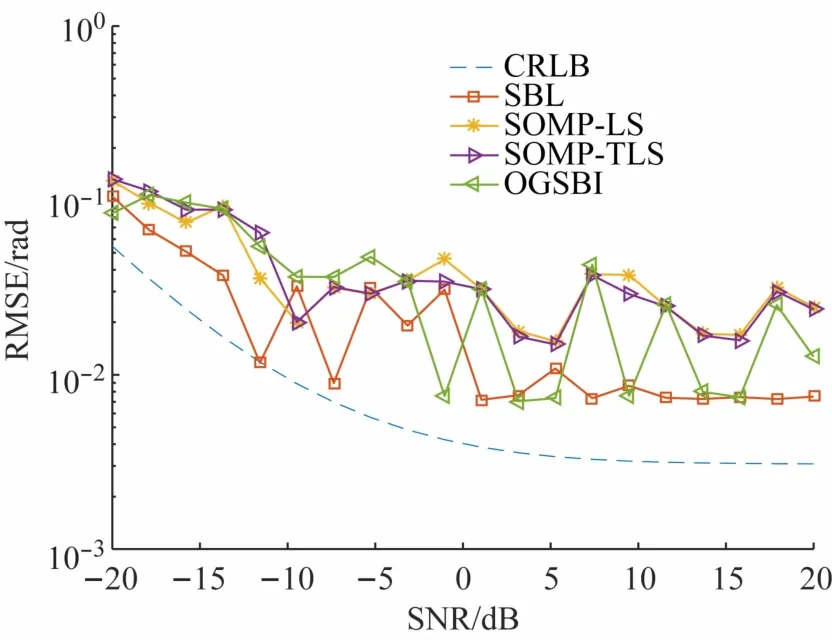
圖3 快拍數為200時，4種算法的RMSE隨SNR的變化

如圖4所示，在信噪比為0dB時，SBL算法的性能明顯優于其他3種算法，在相同條件下，SBL算法的均方根誤差最小，準確率更高。

圖4 SNR＝0 dB時，4種算法的RMSE隨快拍數的變化

4 結 語

通過使用SBL算法進行基于互質陣列的欠定寬帶在未知噪聲場中的DOA估計，與SOMP_LS，SOMP_TLS和OGSBI算法相比，SBL表現出出色的檢測性能和估計準確度。SBL可以容納由互質陣列提供增加的DOF，對欠定寬帶進行有效的DOA估計，通過互質陣列提供的虛擬陣元接收更多的寬帶信號并且通過每2個向量化函數之間的運算消除未知噪聲。本文采用了定點更新為寬帶DOA估計提供全局收斂性。仿真和實驗結果表明，本文算法有著更好的抗噪能力。