基于T-S模糊故障樹的制動系統(tǒng)可靠性分析

周亞輝， 齊金平，2，3， 李少雄， 王 康（.蘭州交通大學(xué)機(jī)電技術(shù)研究所，蘭州730070；2.甘肅省物流及運輸裝備信息化工程技術(shù)研究中心，蘭州730070；3.甘肅省物流與運輸裝備行業(yè)技術(shù)中心，甘肅蘭州730070）

importance

0 引 言

目前，中國高鐵總里程已達(dá)3.5萬km，占世界總里程的70%左右，運營規(guī)模龐大，且正處于從大規(guī)模建設(shè)階段向全面運維維護(hù)階段轉(zhuǎn)變。隨著動車組服役時間的增長與性能的退化，高速鐵路的運營安全及維修壓力將逐步凸顯，對其進(jìn)行可靠性分析性的必要也進(jìn)而提升。制動系統(tǒng)是動車組的主要系統(tǒng)之一，主要由電制動和空氣制動兩大部分組成［1］，電制動是將牽引電機(jī)職能轉(zhuǎn)換成發(fā)電機(jī)來完成制動，而空氣制動是將相應(yīng)的電信號轉(zhuǎn)換成空氣信號，從而輸出空氣施加實現(xiàn)功能。雖然制動系統(tǒng)可靠性相對較高，但是由于其結(jié)構(gòu)復(fù)雜，運營環(huán)境多變，也經(jīng)常出現(xiàn)一些故障，一旦某一環(huán)節(jié)故障導(dǎo)致制動失效，整車的安全性將被危及，甚至出現(xiàn)重大事故，因此，有必要對制動系統(tǒng)進(jìn)行可靠性分析評估，消除潛在隱患，保證其安全運行。

故障樹分析法（FTA）是可靠性研究常用方法之一，傳統(tǒng)的基于布爾代數(shù)和概率論的故障樹分析方法［2］，已經(jīng)廣泛使用，但其故障概率精確已知、邏輯門之間必須聯(lián)系明確等條件限制了其在可靠性分析以及故障診斷中的應(yīng)用。Tanaka等［3］對模糊理論首次引用到FTA中，使用模糊乘法代替了傳統(tǒng)的邏輯運算，使其更加簡單，且符合實際，但仍屬于與或邏輯運算。Lin等［4］用以事件的｛0，1｝邏輯表表示事件之間的聯(lián)系，模糊門得以形成，但故障程度不同，后果不同，傳統(tǒng)的｛0，1｝已經(jīng)不能滿足問題分析。宋華等［5］首次提出T-S模糊故障樹，使得故障概率的不確定性得以解決，但不利于專家知識和操作經(jīng)驗的融入。

本文結(jié)合動車組制動系統(tǒng)，以模糊數(shù)描述故障程度，以模糊可能性表達(dá)零部件故障率，構(gòu)建T-S模糊門，既考慮到故障程度對系統(tǒng)的影響，也解決了事件之間的不確定性問題。同時，引入基于信心指數(shù)的專家經(jīng)驗，解決故障數(shù)據(jù)的缺失和多源異構(gòu)問題。最后，對導(dǎo)致故障發(fā)生的基本事件進(jìn)行重要度計算和分析，為制動系統(tǒng)的維修和設(shè)計改造提供參考。

1 T-S模糊故障樹

1.1 事件描述

系統(tǒng)中零部件故障的歷史數(shù)據(jù)是計算故障率的基礎(chǔ)，對于數(shù)據(jù)的不確定性屬性，結(jié)合模糊數(shù)學(xué)描述故障程度即可。若將隸屬函數(shù)描述為四邊形隸屬函數(shù)［6］，表示為

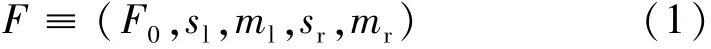
式中：F0是模糊數(shù)支撐集中心；sl和sr是支撐半徑；ml和mr是模糊區(qū)。

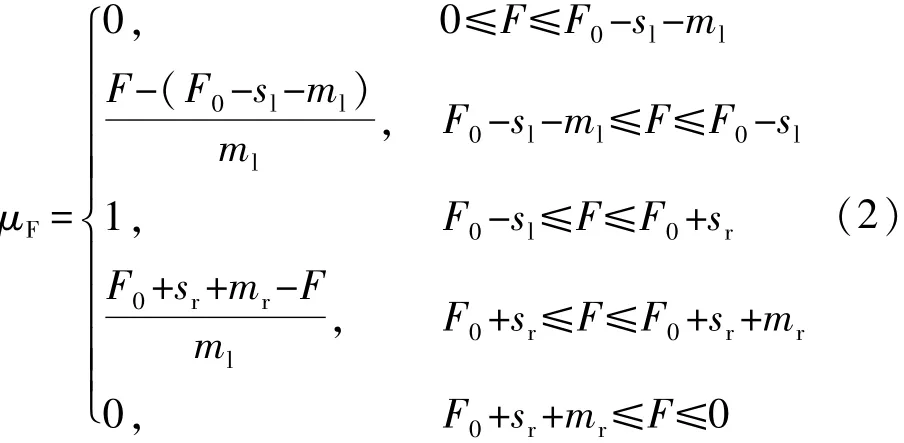
模糊數(shù)的隸屬函數(shù)如圖1所示。由圖1可得：當(dāng)sl＝sr＝0時，四邊形隸屬函數(shù)變成三角函數(shù)；sl＝sr＝ml＝mr＝0時，模糊數(shù)變成確定數(shù)。部件的故障程度在0～1之間取值，本文用模糊數(shù)0、0.5、1.0來描述，一般情況下，sl＝sr，ml＝mr。

圖1 模糊數(shù)的隸屬函數(shù)

1.2 T-S模糊門

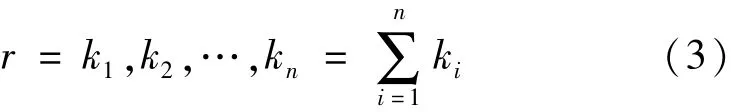
因而，得y（中間事件）的模糊可能性為：

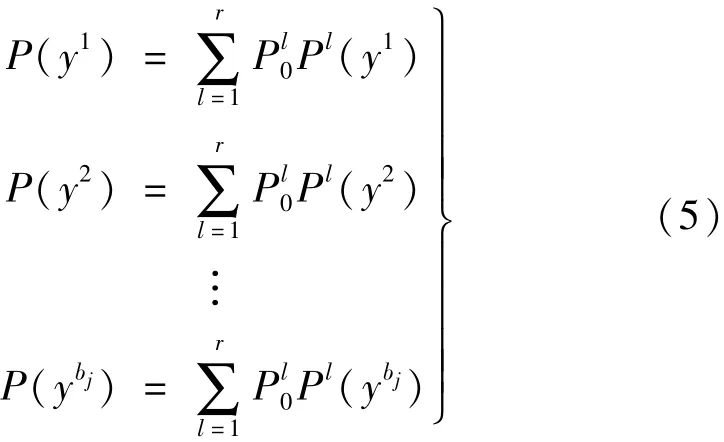
若已得基本事件x1～xn的故障狀態(tài)，則上級事件出現(xiàn)故障的可能性為

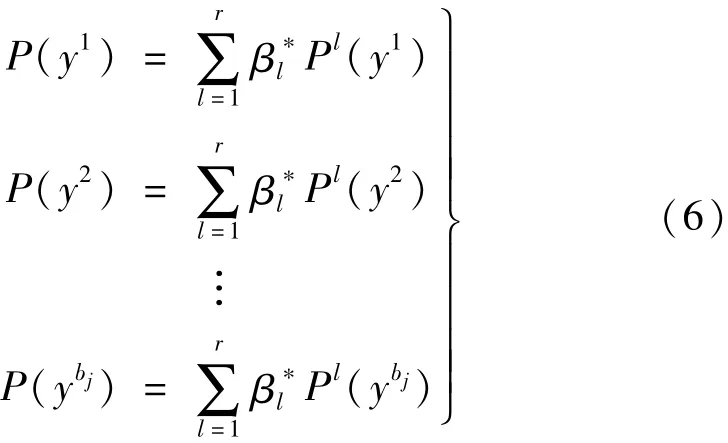
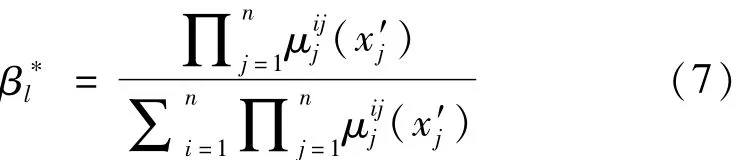
重要度作為可靠性分析的重要參數(shù)之一，反映的是最小割集故障時對系統(tǒng)發(fā)生故障的概率貢獻(xiàn)［9］，是系統(tǒng)零部件的可靠性參數(shù)以及結(jié)構(gòu)函數(shù)，應(yīng)用廣泛，表述如下：

若已知部件xj在故障狀態(tài)為時的失效可能模糊子集為，隸屬函數(shù)μp~x iij，對頂事件T為Tq的T-S模糊重要度為

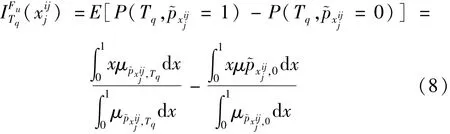
部件xj對頂事件T為Tq的T-S概率重要度為

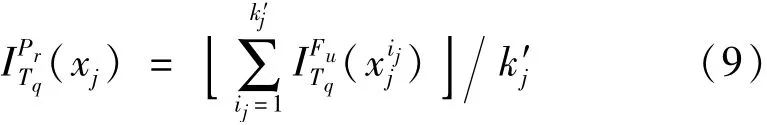
式中，k′j表示第j個非零事件故障狀態(tài)的個數(shù)。

2 制動系統(tǒng)可靠性分析

本文以動車組制動系統(tǒng)中故障頻次較高的部件為主，建立模糊故障樹如圖2所示。各事件代號含義如表1所示。

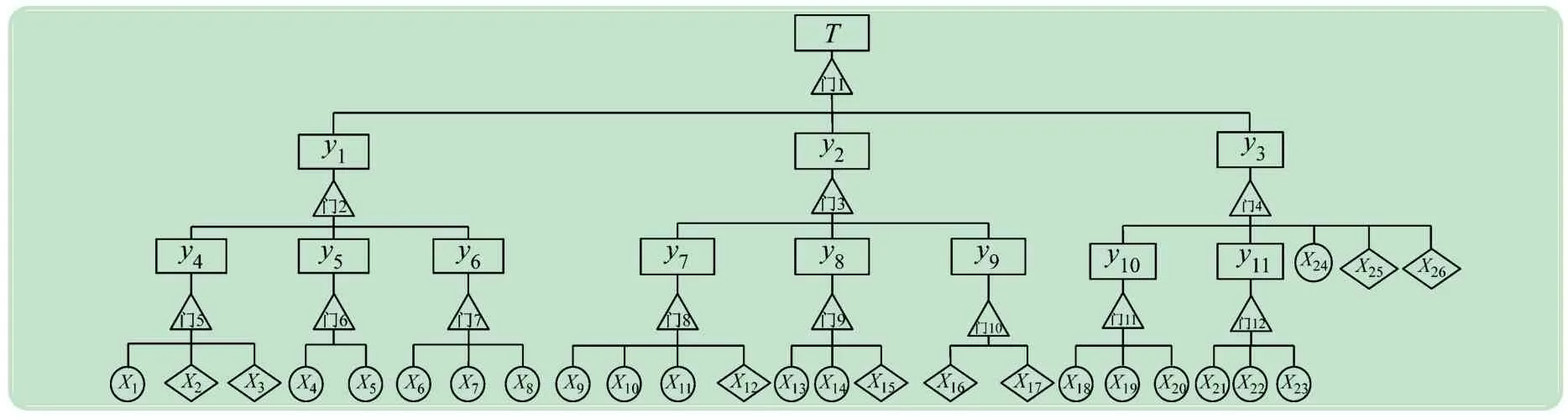
images/BZ_32_435_1145_2043_1607.png

表1 事件代碼表

根據(jù)故障情況，設(shè)制動系統(tǒng)T-S模糊故障樹事件x1～x6，x21～x24和y4，y5，y11存在（0，1）兩種故障狀態(tài)，隸屬函數(shù)sl＝sr＝0.25，ml＝mr＝0.5，x7～x20，x25，x26和y1～y3，y6～y10存在（0，0.5，1）3種故障狀態(tài)，隸屬函數(shù)sl＝sr＝0.1，ml＝mr＝0.3。依據(jù)歷史故障數(shù)據(jù)以及專家經(jīng)驗，得部分T-S模糊門如表2～4所示。

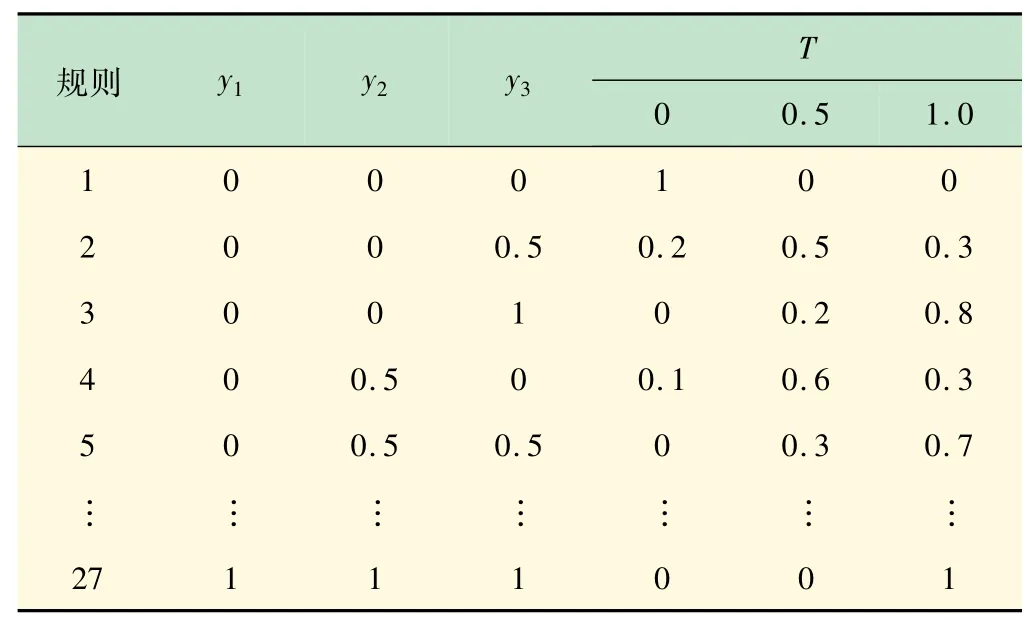
表2 T-S模糊門1

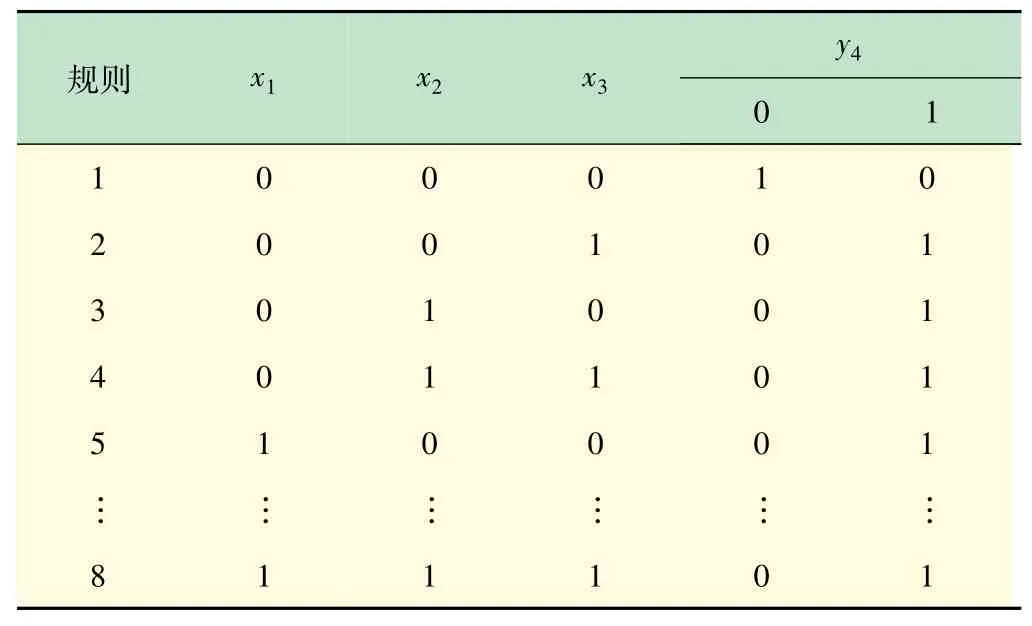
表4 T-S模糊門5

基于動車組運行統(tǒng)計數(shù)據(jù)以及信心指數(shù)修正的專家調(diào)查法［10-13］，可得表5中各部件故障率。假設(shè)故障程度為0.5的故障率與故障程度為1時的相等［14-17］。

2.1 已知部件故障模糊可能性，計算系統(tǒng)故障的模糊可能性

依據(jù)表5與式（4）、（5），可得到中間事件的模糊可能性如下：

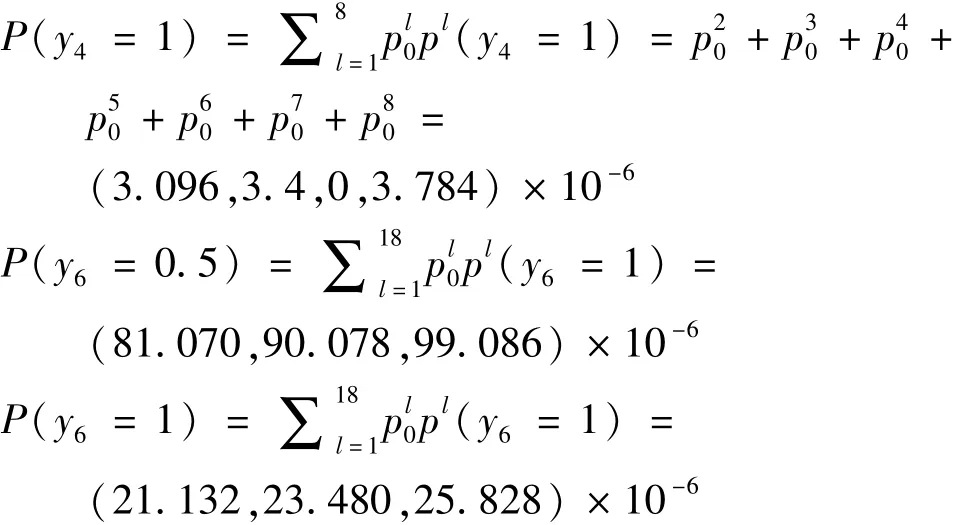
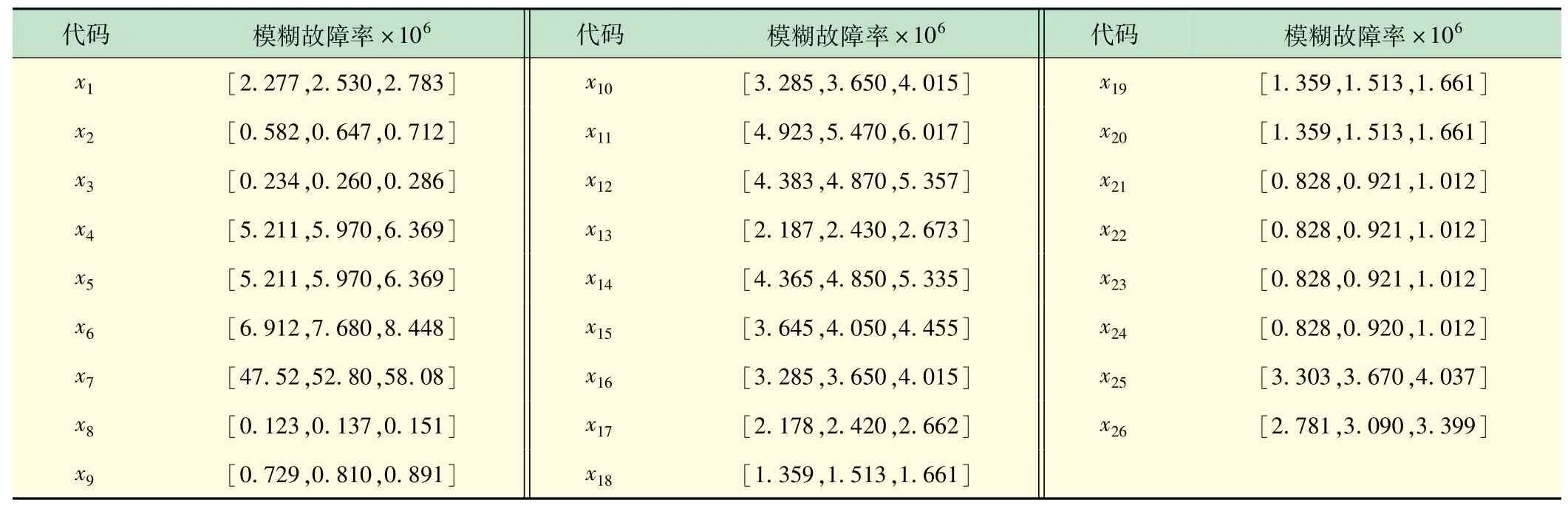
表5 制動系統(tǒng)各基本事件的模糊故障率

同理，計算出其他事件的模糊可能性如表6所示。

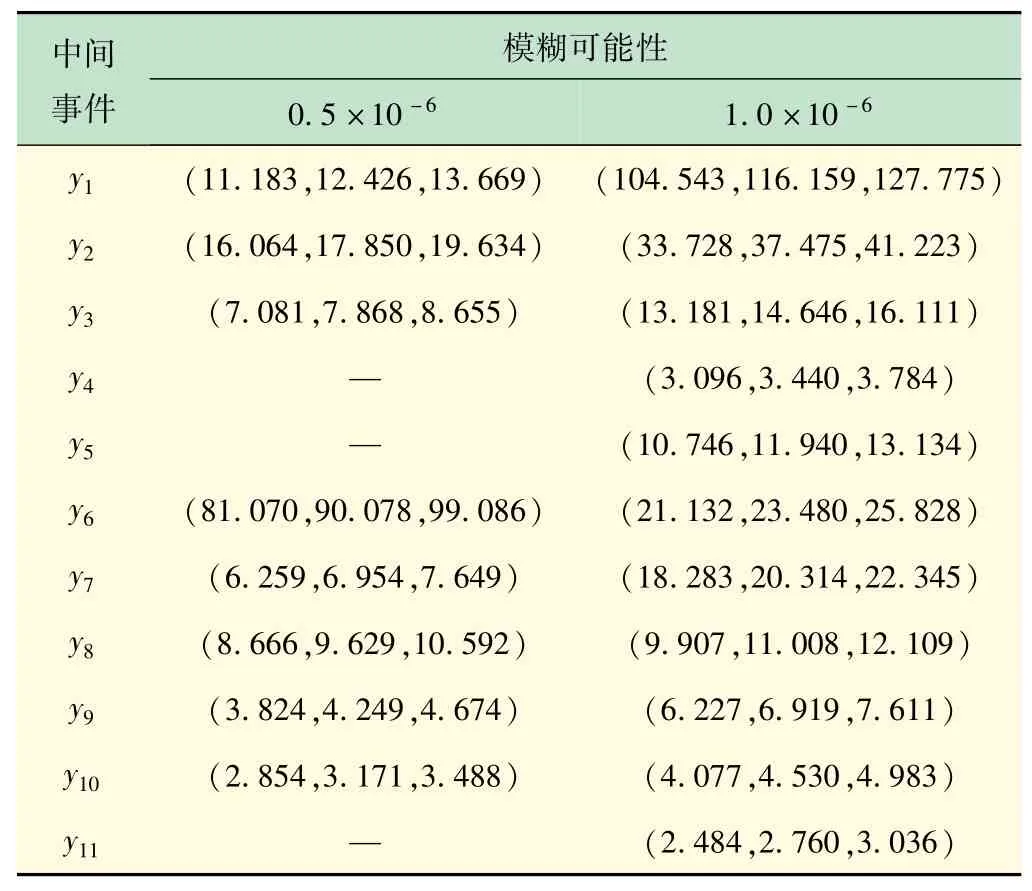
表6 中間事件模糊可能性

計算得頂事件T的模糊可能性為：

由結(jié)果可知，制動系統(tǒng)故障的模糊可能性與各個部件的模糊可能性為同一數(shù)量級，且電磁閥、滑行檢測單元、制動盤等部件發(fā)生故障的模糊可能性遠(yuǎn)小于TS模糊故障樹中頂事件發(fā)生故障的模糊可能性，與實際一致。

2.2 已知部件故障狀態(tài)，計算系統(tǒng)故障的模糊可能性

假設(shè)部件的故障狀態(tài)分別為：x1～x6＝0，x7＝0.4，x8＝0.1，x9＝0.1，x10＝0.2，x11＝0.3，x12＝0.3，x13＝0.2，x14＝0.3，x15＝0.3，x16＝0.2，x17＝0.2，x18＝0.1，x19＝0.1，x20＝0.1，x1～x6＝0，x25＝0.2，x26＝0.2。根據(jù)式（6）、（7）可得：

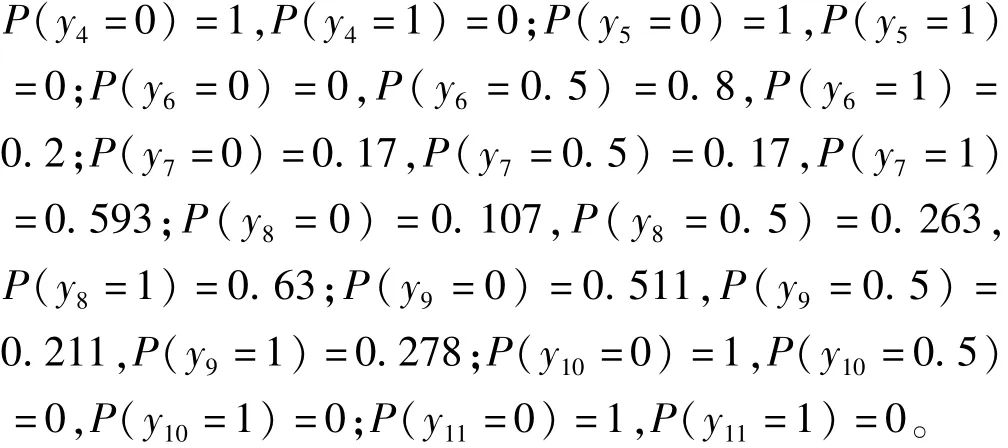
用式（4）、（5）計算y1，y2，y3，則根據(jù)表3、4可得：P（y1＝0）＝0，P（y1＝0.5）＝0.8，P（y1＝1）＝0.2；P（y2＝0）＝0.015 6，P（y2＝0.5）＝0.037 9，P（y2＝1）＝0.946 5。

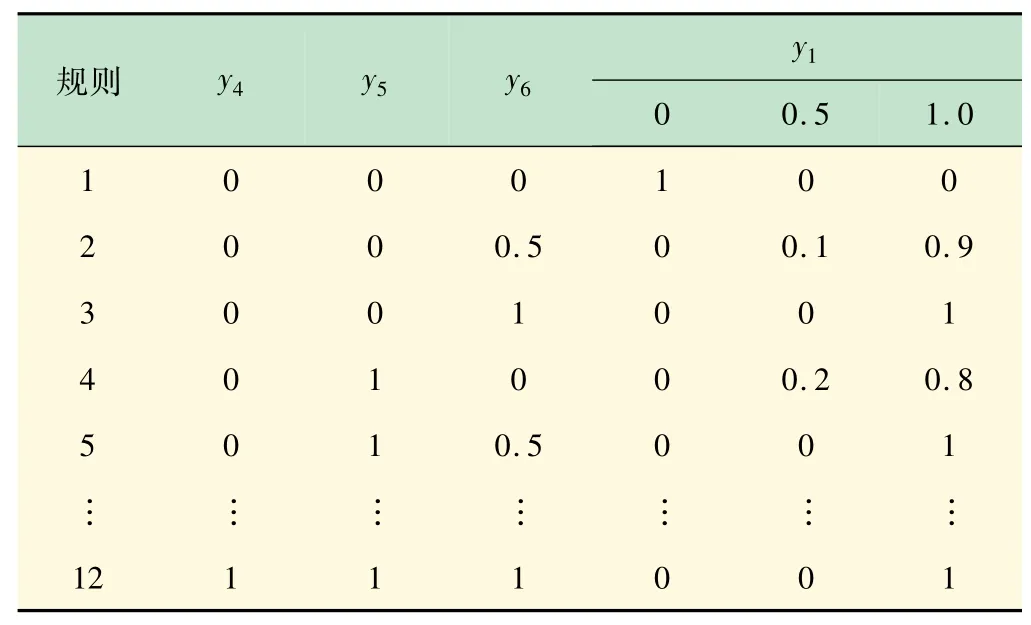
表3 T-S模糊門2

以y11的模糊可能性代替隸屬度計算，可得到y(tǒng)3的模糊故障率如下：

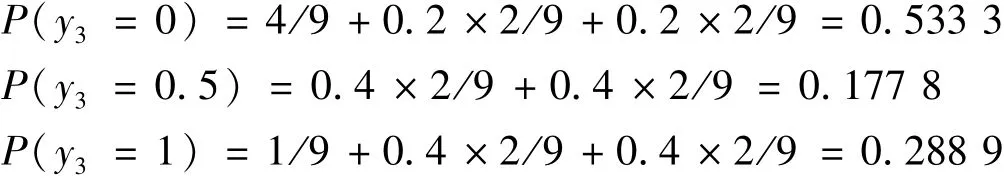
故頂事件故障概率為：

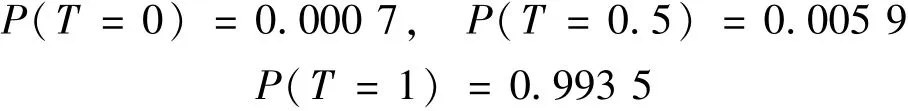
經(jīng)過分析可知，閘片出現(xiàn)故障時，系統(tǒng)的故障程度與其基本一致。所以可根據(jù)部件的故障程度結(jié)合T-S模糊故障樹得知系統(tǒng)故障可能性。

2.3 基于T-S模糊故障樹的制動系統(tǒng)重要度分析

根據(jù)式（8）可得x11對T為0.5和1故障狀態(tài)的TS模糊重要度分別為

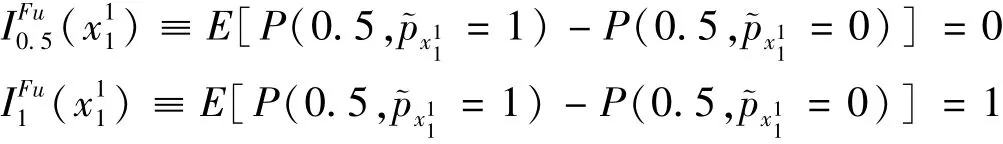
同理得x2～x26的T-S模糊重要度見表7。

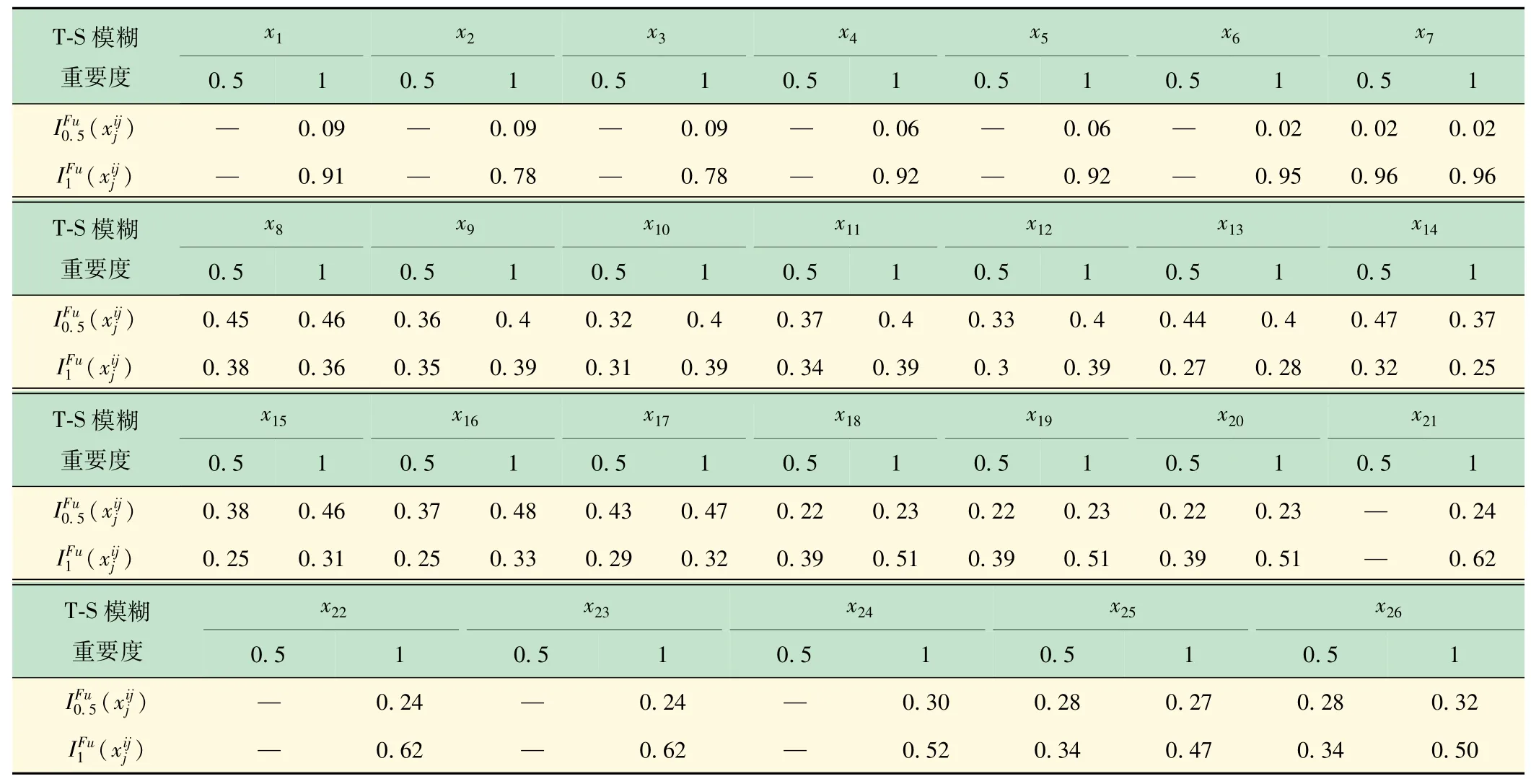
表7 T-S模糊重要度

根據(jù)式（9）可得x7對T為0.5和1故障狀態(tài)的TS概率重要度分別為：

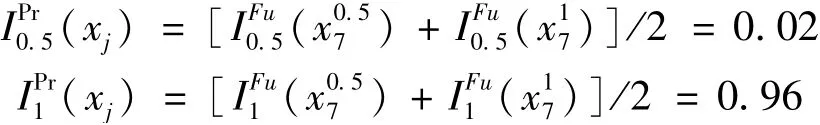
同理得出x1～x26的T-S概率重要度見表8。由表8可知，系統(tǒng)為輕微故障時，重要度大小為x8＞x17＞x16＞x15（x13，x14）＞x11＞x9＞x12＞x10＞x26＞x25＞x18（x19，x20）＞x24＞x21（x22，x23）＞x1（x2，x3）＞x4（x5）＞x7＞x6；當(dāng)系統(tǒng)為嚴(yán)重故障時，重要度大小為x7＞x6＞x5＞x4＞x1＞x18（x19，x20）＞x26＞x25＞x2＞x3＞x8（x9，x11）＞x10（x12）＞x17（x21，x22，x23）＞x16（x14）＞x15（x13）＞x24。重要度大的部件為系統(tǒng)的薄弱環(huán)節(jié)，所得結(jié)果與實際相符，主要原因是閘片由于過度磨損，常出現(xiàn)缺陷和裂紋，而風(fēng)管又容易被砂石等擊打而導(dǎo)致破裂漏風(fēng)，空氣壓縮機(jī)經(jīng)常使用容易出現(xiàn)滲油等現(xiàn)象，因而故障率也較高。

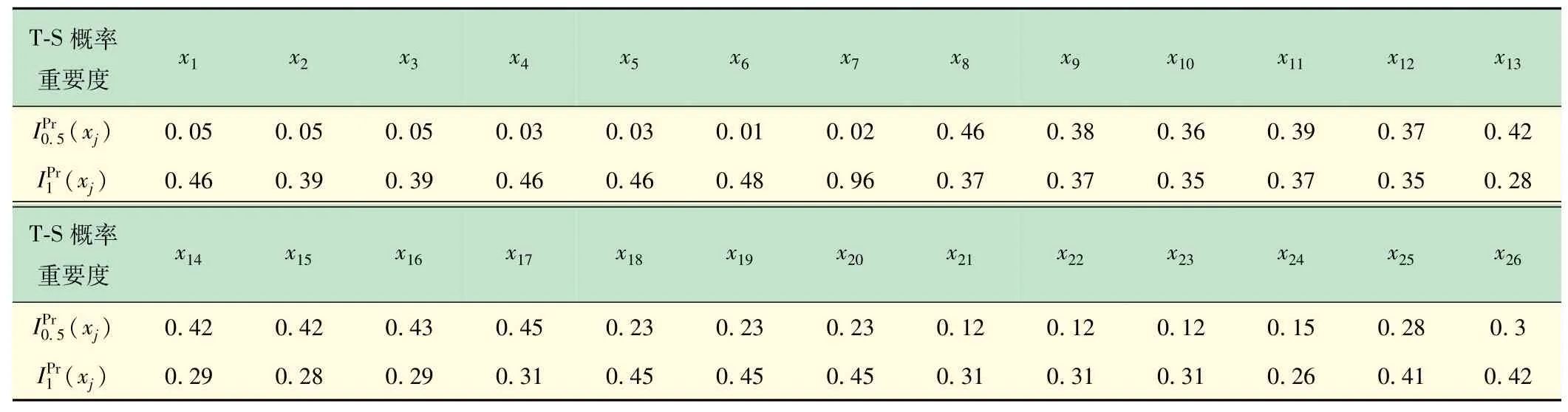
表8 T-S概率重要度

3 結(jié) 論

（1）利用T-S模糊故障樹對動車組制動系統(tǒng)進(jìn)行可靠性分析，用T-S模糊門描述事件的邏輯關(guān)系，克服了二態(tài)失效分析難以找到部件之間緊密聯(lián)系的局限，綜合了所有失效故障狀態(tài)對系統(tǒng)的影響，所得結(jié)果更加符合工程實際且更一般化。

（2）由于T-S模糊故障樹邏輯簡單緊密，所需數(shù)據(jù)較少，使故障樹建樹的難度進(jìn)一步降低，同時結(jié)合基于信心指數(shù)修正的專家調(diào)查法，得到頂事件的故障率區(qū)間和基本事件的模糊重要度，找出了系統(tǒng)的薄弱環(huán)節(jié)，可為系統(tǒng)檢修提供參考。

（3）T-S模糊故障樹可在部件失效概率未知的情況下，僅憑借失效部件故障狀態(tài)計算系統(tǒng)的失效可能性。