內圈傾斜角對高速角接觸球軸承動態特性的影響

常麗萍，常亞南，楊雷雷

(1.中車株洲電機有限公司，湖南 株洲 412000；2.洛陽軸承研究所有限公司，河南 洛陽 471000；3.長沙景嘉微電子股份有限公司，湖南 長沙 410000)

0 引言

角接觸球軸承在武器裝備、軍用車輛等領域有著廣泛應用，是關鍵零部件之一。隨著對主機性能要求的不斷提高，對與之配套的角接觸球軸承性能要求也越來越高。實際工程中，由于加工裝配誤差和運轉時軸的撓曲變形不可避免，導致軸承內外套圈發生相對傾斜[1]。若軸承內外圈之間存在傾斜角，則必將影響軸承動態性能，降低軸承旋轉精度，從而影響軸承使用壽命，甚至造成軸承卡死，引起軸承早期失效[2]。

國外對套圈傾斜角接觸球軸承的研究開始較早。Ellis[3]對球軸承套圈傾斜進行了研究，并論述了套圈傾斜產生的原因、可能的影響及傾斜故障的診斷方法，提出避免傾斜問題的經驗性措施。Hinton[4-5]對航空發動機球軸承因保持架疲勞斷裂而失效的案例進行了分析，通過大量實測統計數據發現套圈傾斜是主要原因之一。Crawford[6]對套圈傾斜狀態下軸承保持架的應力進行測試，發現當套圈傾斜角從15.6′增加到36.6′時，軸承保持架的應力波動量從1.8 MPa增加到35.2 MPa，進一步證實了Hinton的結論。Ertas等[7]結合試驗與計算機仿真研究了套圈傾斜對軸承徑向剛度的影響，通過分析轉子系統的特征頻率與臨界轉速，發現套圈固定的傾斜角會增加軸承的徑向剛度。Bugra等[8]通過實驗測試和轉子動力學計算機建模，給出了不同軸向載荷工況條件下套圈發生傾斜時的角接觸球軸承徑向剛度。Damian等[9]通過數值計算方法研究了內圈傾斜角對軸承載荷分布的影響。Oktaviana等[10]研究了內圈傾斜角對角接觸球軸承打滑影響，發現在定位預緊下內圈傾斜角不會增大軸承打滑。張學寧等[11]研究了套圈傾斜角對軸承接觸角的影響規律，發現套圈傾斜時接觸角沿位置角分布不均，且這些現象隨套圈傾斜角的增大而愈發明顯。周陽[12]編制了考慮安裝誤差的角接觸球軸承計算軟件。熊萬里等[13]研究了高速角接觸球軸承套圈傾斜角允許范圍，但其未考慮工況因素的影響。張進華等[14]和方斌等[15]研究了聯合載荷作用下高速角接觸球軸承快速計算方法并對接觸角變化進行分析。盡管針對內圈傾斜角問題國內外學者開展了上述工作，但大多數學者的分析均假設軸承在單一工況下運行，沒有涉及轉速、軸向載荷、聯合載荷及滾珠材料等應用條件改變時內圈傾斜角對軸承動態特性的影響分析。然而工程應用條件十分復雜，軸承在單一工況下運行的情況并不常見，且近年來氮化硅陶瓷滾動體軸承逐漸被廣泛應用，因此迫切需要全面地研究不同工況條件下及滾動體材料為氮化硅陶瓷時內圈傾斜角對軸承動態特性的影響規律，為工程應用提供理論指導。

本文使用赫茲接觸理論建立了一種綜合考慮內圈傾斜角、高速離心效應的軸承分析計算模型，采用Newton-Raphson迭代法對模型求解，開發了適用于內圈傾斜條件的高速角接觸球軸承動態性能分析軟件。在此基礎上，系統研究了復雜工況內圈傾斜角對軸承接觸角、套圈最大接觸應力(簡稱接觸應力)、旋滾比、滾珠公轉轉速以及剛度的影響規律。

1 內圈傾斜球軸承建模理論與方法

1.1 幾何分析

假定軸承外圈固定，隨軸旋轉的內圈可相對外圈移動。當內圈相對外圈傾斜時，軸承一般會同時承受軸向負荷、徑向負荷和力矩，套圈不同位置處各組件之間的幾何關系將發生變化。軸承滾珠角位置如圖1所示。圖1中，dm為軸承中徑，軸承每個滾珠都對應1個編號，編號為j的滾珠位置角ψj=360(j-1)/Z，j≤Z，Z為滾珠數目。

圖1 滾珠角位置

圖2為位置角ψj處，軸承運轉前后套圈滾道溝曲率中心與球心相對位置的變化。圖2中，δa表示軸向位移，δr表示徑向位移，θ表示內圈傾斜角，A為外圈滾道溝曲率中心位置，保持固定不變，B點為球中心最初位置，B′為軸承運動平衡狀態球中心最終位置，C點為內滾道溝曲率中心最初位置，C′點為軸承運動平衡狀態內滾道溝曲率中心位置，α0為軸承初始接觸角，αij和αej分別為軸承運動平衡狀態滾珠內、外接觸角，Aaj、Arj分別為軸承運動平衡狀態內溝道曲率中心在軸向和徑向的分量，Xaj、Xrj分別為軸承運動平衡狀態球中心位置在軸向和徑向的分量，Δij為內溝道曲率中心與球中心運轉平衡位置之間的距離，Δej為外溝道曲率中心與球中心運轉平衡位置之間的距離，Ri為內滾道溝曲率中心軌跡的半徑，uc為軸承內圈的離心膨脹量，BD為軸承靜止時內、外溝道曲率中心的距離。

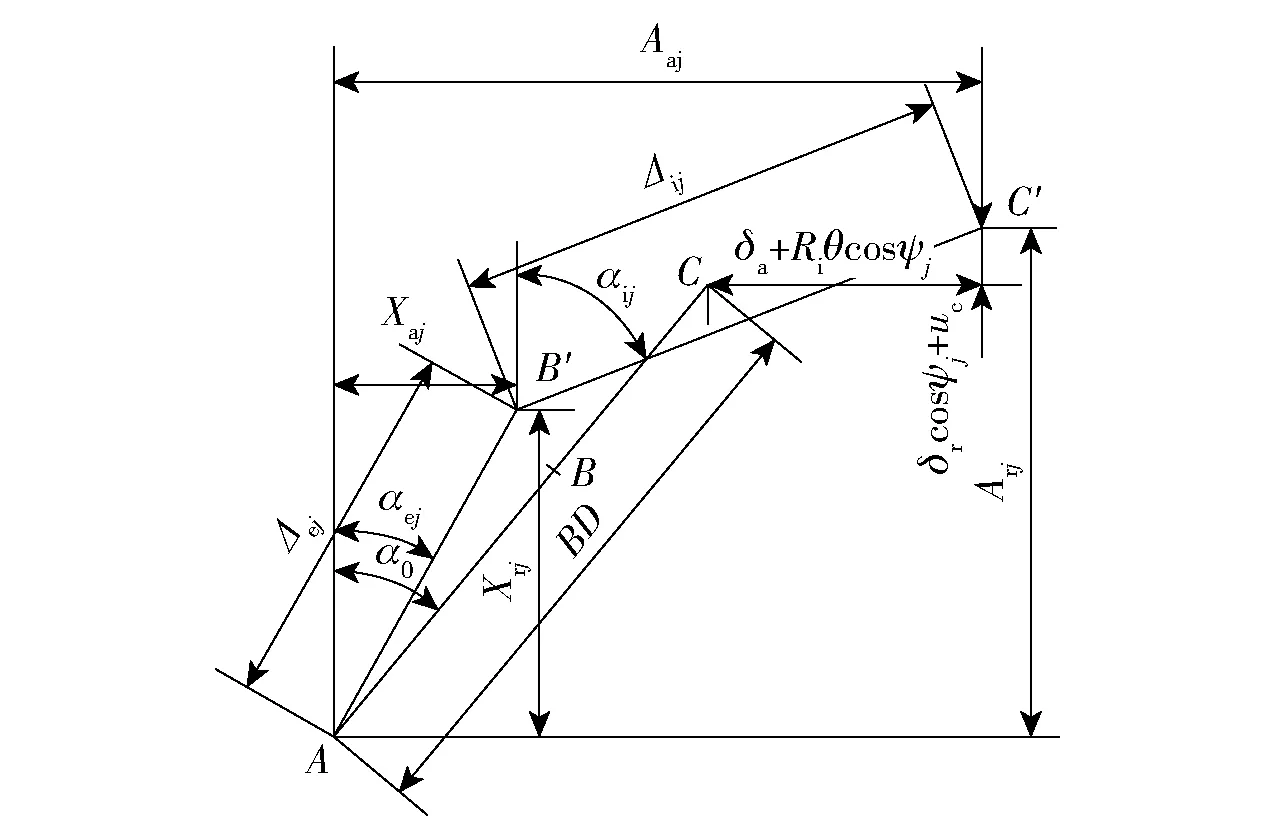
圖2 滾珠j位移圖

軸承內圈高速旋轉產生離心膨脹，軸承內圈的離心膨脹量uc[16]表示為

(1)

式中:ρ為材料密度；ω為轉速；E為材料楊氏模量；d為軸承內徑；υ為材料泊松比。

軸承運行時，內外溝道曲率中心與球中心運轉平衡位置之間的距離為

Δij=(fi-0.5)Dw+δij，

(2)

Δej=(fe-0.5)Dw+δej，

(3)

式中:fi、fe為內、外滾道溝曲率半徑系數；Dw為滾珠直徑；δij、δej為第j個滾珠與內外滾道間的接觸變形。

變形后，軸承內、外溝道曲率中心間距離在軸向和徑向分量分別表示為

Aaj=(fi+fe-1)Dwsinα0+δa+Riθsinψj，

(4)

Arj=(fi+fe-1)Dwcosα0+δrcosψj+uc，

(5)

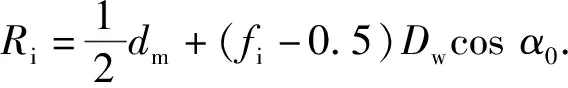
運行時，第j個滾珠與內、外滾道接觸角可通過(6)式得到

(6)

根據勾股定理，得到變形協調方程組如下：

(Aaj-Xaj)2+(Arj-Xrj)2-[(fi-0.5)Dw+δij]2=0，

(7)

(8)

1.2 受力分析

高速角接觸球軸承中，球的離心力引起接觸變形和接觸角變化，加之球自轉軸線不斷變化引起陀螺力矩和相應摩擦阻力，計算復雜。考慮通過軸承軸線和方位角ψj處球中心的平面，作用于球的載荷和力矩如圖3所示。圖3中：Mgj為第j個滾珠所受陀螺力矩，Fcj為第j個滾珠的離心力，Qij、Qej分別為滾珠與滾道之間的法向接觸力；λij、λej為求解系數。

圖3 滾珠受力平衡

滾珠與滾道之間的法向接觸力表示為

(9)

式中：Kij、Kej為第j個滾珠與內外滾道間的負荷變形系數。

根據圖3所示第j個滾珠的受力平衡情況，可以列出滾珠的平衡方程組為

(10)

Qijcosαij-Qejcosαej-

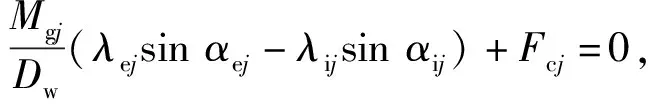
(11)

根據滾珠與軸承內圈的力學關系，列出軸承內圈的平衡方程為

(12)

(13)

式中:Fa為軸承所受軸向負荷；Fr為軸承所受徑向負荷。

2 模型求解

根據第1節模型，采用Newton-Raphson迭代法對模型求解對該動剛度模型進行求解，按照圖4算法設計開發了計算程序，求解精度ε=10-5.需要說明的是，內圈傾斜角θ并不是作為一個未知量經迭代求解得出，而是通過預先給定它的值來研究內圈傾斜角對軸承動態特性的影響規律。采取這種處理方式有兩個原因：1)內圈傾斜角通過實驗測試的方法易于獲得；2)內圈傾斜角對軸承動態特性的影響很大，如果將其作為迭代求解的未知量，則很難得出收斂的結果。

圖4 角接觸球軸承算法設計

3 計算結果與分析

使用自編程序與ROMAX軟件對7206軸承(基本結構參數見表1)計算實例進行對比，對比結果如圖5所示。由于ROMAX軟件輸出中不包含諸如軸承的旋滾比、滾珠公轉轉速和動剛度等參數結果，僅對軸承接觸角和內、外圈最大接觸應力進行對比。從表1中的對比數據來看，本文計算結果與ROMAX軟件的計算結果十分吻合，最大計算差距3.7%.由此表明，本文分析模型所編制的程序可用于后續的分析。

表1 軸承結構參數

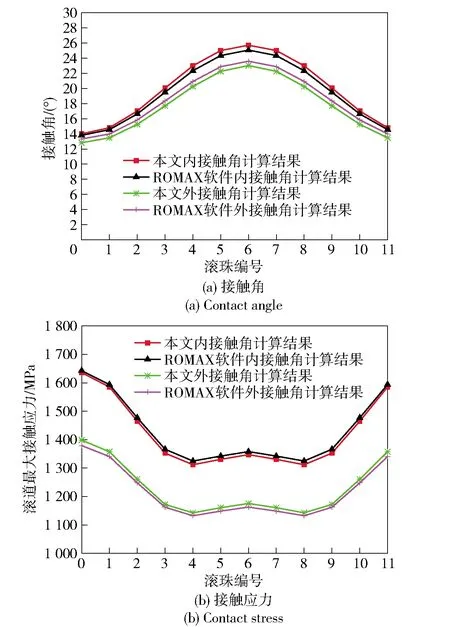
圖5 計算結果對比

以7008軸承(基本結構參數見表1)為例開展研究。通過對接觸角、接觸應力、旋滾比、滾珠公轉速度、剛度5個項點進行計算分析表征軸承動態特性變化。

3.1 內圈傾斜角對不同轉速工況下軸承動態特性的影響

觀察圖6(a)、圖6(b)可知，內圈傾斜角引起軸承內、外圈接觸角波動變化，不同轉速下波動規律基本一致，表明內、外圈接觸角波動主要受內圈傾斜角影響，轉速對其影響不大。

觀察圖6(c)、圖6(d)可知，隨轉速升高，內圈傾斜角所引起的軸承接觸應力波動變弱。同樣是6′傾斜角，當轉速為10 000 r/min時，內、外圈最大接觸應力峰值較無內圈傾斜角時分別變化8.0%、8.4%；當轉速為30 000 r/min，內、外圈最大接觸應力峰值較無內圈傾斜角時分別變化5.7%、3.8%.

觀察圖6(e)可知，軸承轉速升高，內圈傾斜角引起旋滾比大幅增加。轉速為10 000 r/min時，有6′傾斜角旋滾比最大值較內圈傾斜前增加了7.8%；轉速為30 000 r/min時，有6′傾斜角旋滾比最大值較內圈傾斜前增加了14.0%.旋滾比增大意味著軸承磨損發熱嚴重。

觀察圖6(f)滾珠公轉轉速隨位置角的變化可知，軸承轉速愈高，內圈傾斜角引起滾珠公轉轉速波動幅度愈大。轉速為10 000 r/min時，6′內圈傾斜角引起滾珠公轉轉速波動最大變化量為80 r/min，占比0.8%；轉速為30 000 r/min時，6′內圈傾斜角引起滾珠公轉轉速波動最大變化量為570 r/min，占比1.9%.這意味著轉速為30 000 r/min時滾珠在公轉周期內會經歷更加劇烈的加速和減速過程。

由以上分析可知，軸承轉速升高，內圈傾斜角所引起的軸承接觸應力波動變弱，但旋滾比、公轉轉速波動變化均增強。這表明在高速下，內圈傾斜角更易引發與軸承熱相關的失效模式，而非常見的疲勞失效。

圖6(g)為軸承動態剛度隨轉速的變化曲線，由圖6(g)可知：無論是否存在內圈傾斜角，隨轉速升高，徑向剛度Kr、軸向剛度Ka和角剛度Kθ均呈下降趨勢，且角剛度下降最快。

圖6 內圈傾斜角對不同轉速軸承動態特性的影響(Fa=1 kN，Fr=0 kN)

3.2 內圈傾斜角對單軸向載荷工況下軸承動態特性的影響

圖7給出了內圈傾斜角為6′時不同軸向載荷軸承動態特性變化曲線。通過觀察可以發現，軸向載荷增加顯著增大內、外接觸角和最大接觸應力，但幾乎不改變波動規律，且隨著軸向載荷增大，增幅放緩。軸向載荷對內圈旋滾比和滾珠公轉轉速影響不大。無論是否存在內圈傾斜角，隨軸向載荷增加，軸承動態剛度變化規律一致[17]。

圖7 內圈傾斜角對單軸向力工況下軸承動態特性的影響(Fr=0 kN, 軸承轉速10 kr/min)

3.3 內圈傾斜角對聯合載荷工況下軸承動態特性的影響

圖8給出了內圈傾斜角對聯合載荷工況軸承動態特性的影響。通過觀察可以發現徑向載荷的作用會引起軸承動態特性波動，存在一個適當的內圈傾斜角將徑向載荷所帶來的接觸角、旋滾比、公轉速度的波動降至最低。圖8(g)為內圈傾斜角對聯合載荷工況下軸承動態剛度的影響曲線，可以看到，內圈傾斜角的存在增大了軸承徑向剛度和角剛度。以上這些變化對軸承穩定運轉是有利的。然而，從圖8(c)、圖8(d)可知，內圈傾斜角會引起軸承套圈最大應力幅值增大，這削弱了軸承徑向承載能力。盡管如此，在對軸承徑向承載能力要求低的應用場合，通過適當初始內圈傾斜角使軸承非均勻預緊[18]，可降低軸承磨損和發熱，增大軸承動態剛度，提高主機運轉穩定性。

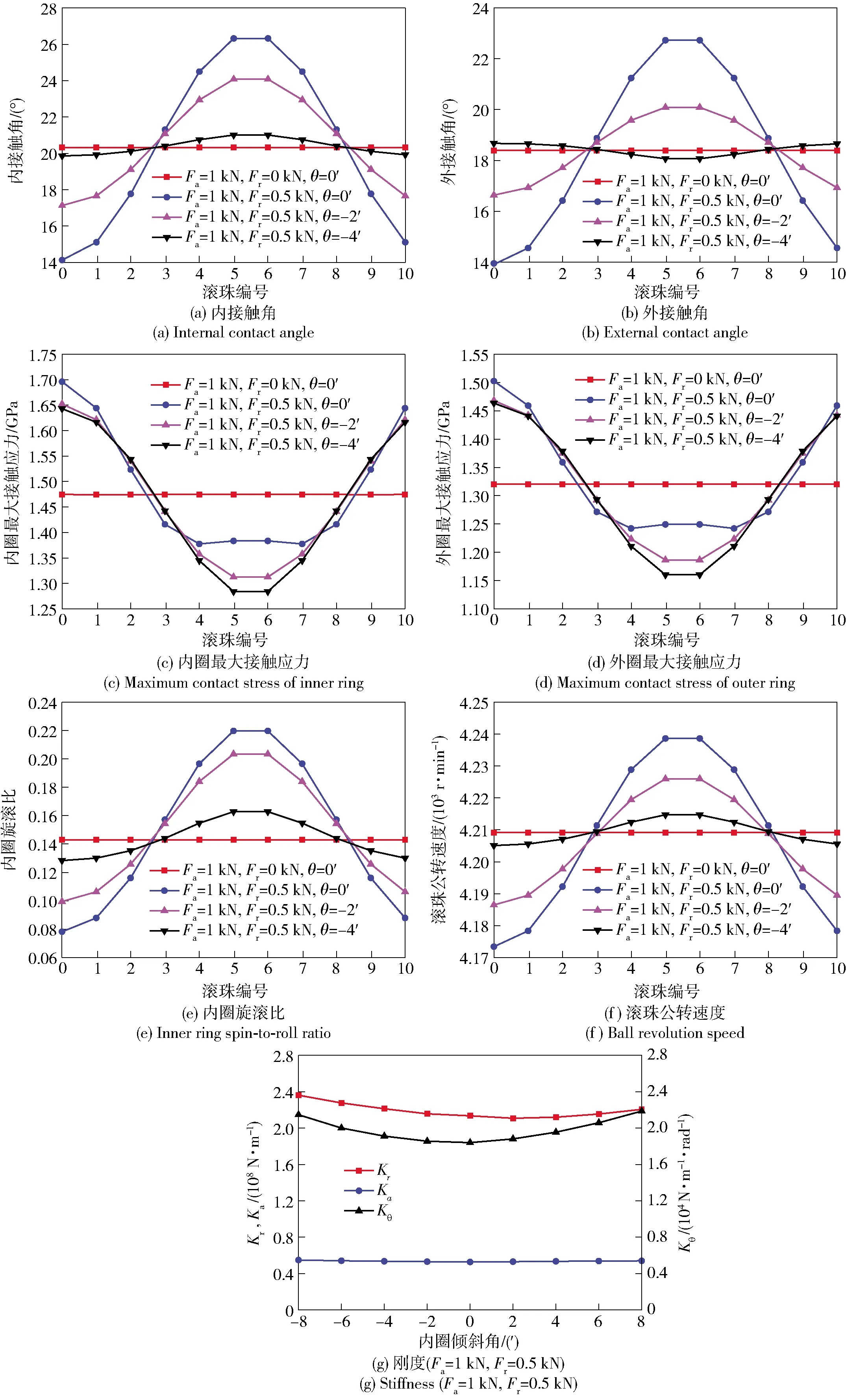
圖8 內圈傾斜角對聯合載荷工況下軸承動態特性的影響(軸承轉速10 kr/min)

3.4 內圈傾斜角對不同材料滾動體軸承動態特性的影響

內圈傾斜角對不同材料滾動體軸承動態特性的影響如圖9所示。由圖9可知，受內圈傾斜角影響，氮化硅陶瓷球軸承內、外圈接觸角波動較鋼球軸承小，氮化硅陶瓷球軸承旋滾比和滾珠公轉轉速也遠小于鋼球軸承。圖9(g)、圖9(i)為不同滾珠材料軸承動態剛度變化曲線，從中可以看到，氮化硅陶瓷球軸承的動態剛度大于鋼球軸承，隨轉速提高，氮化硅陶瓷球軸承動態剛度下降速度小于鋼球軸承。此外，無論是鋼球軸承還是氮化硅陶瓷球軸承，軸承徑向剛度和角剛度因內圈傾斜角作用而顯著增加，軸向剛度受內圈傾斜角影響較小，幾乎沒有改變。相同的工況下，陶瓷球軸承比鋼球軸承有著相當多的優勢，具有更低的磨損和發熱、更高的剛度及運轉穩定性。

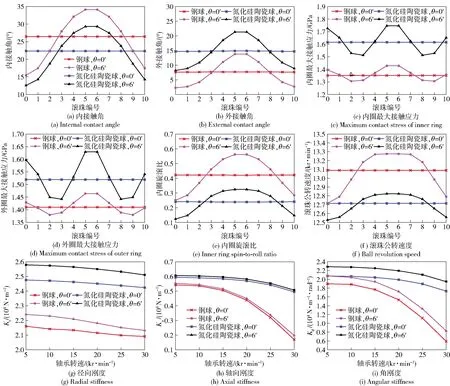
圖9 內圈傾斜角對不同材料滾動體軸承動態特性的影響(Fa=1 kN, Fr=0 kN，軸承轉速30 kr/min)

盡管如此，從圖9(c)、圖9(d)可見，氮化硅陶瓷球軸承接觸應力對內圈傾斜角更加敏感，受內圈傾斜角影響接觸應力波動更強烈，徑向承載能力下降更多。可以看到，有6′傾斜角時：氮化硅陶瓷球軸承內、外圈最大接觸應力峰值較無內圈傾斜角時分別變化8.0%、7.2%；鋼球軸承內、外圈最大接觸應力峰值較無內圈傾斜角時分別變化5.6%、3.8%.鑒于此，使用氮化硅陶瓷球軸承時，應更加嚴格地控制軸承配合件的形位公差，減小安裝后內圈傾斜，否則易造成軸承提前失效。

4 結論

本文給出一種綜合考慮內圈傾斜角、高速離心效應的軸承分析計算模型，采用Newton-Raphson法求解該模型，研究了內圈傾斜角對高速角接觸球軸承接觸角、接觸應力、旋滾比、滾珠公轉轉速以及剛度的影響。得出如下主要結論：

1)軸承轉速升高，內圈傾斜角所引起的軸承接觸應力波動變弱，但旋滾比、公轉轉速波動變化均增強。這表明在高速下，內圈傾斜角更易引發與軸承熱相關的失效模式，而非常見的疲勞失效。

2)對于承受聯合載荷的角接觸球軸承，適當的初始內圈傾斜角可大幅降低由徑向載荷所帶來的接觸角、旋滾比、公轉速度的波動，顯著增大軸承徑向剛度和角剛度，但同時也會減弱軸承徑向承載能力。因此，在某些對軸承徑向承載能力要求低的應用場合，通過適當初始內圈傾斜角使軸承非均勻預緊，可在一定程度上降低軸承磨損和發熱，增大軸承動態剛度，提高主機運轉穩定性。對于本文所研究的軸承及對應的工況，-4′的內圈傾斜角可最大程度減弱由徑向載荷帶來的軸承動態特性不均勻分布。

3)內圈存在傾斜角時，氮化硅陶瓷球軸承在接觸角、內圈旋滾比、公轉轉速、動態剛度方面表現均優于鋼球軸承，但與鋼球軸承相比接觸應力受內圈傾斜角影響波動更加劇烈，徑向承載下降較多。因此，使用氮化硅陶瓷球軸承時，應更加嚴格地控制軸承配合件的形位公差，減小安裝后內圈傾斜，否則易造成軸承提前失效。