四旋翼無人機反步積分自適應控制器設計

王慧東，周來宏

(1.包頭職業技術學院 數控技術系，內蒙古 包頭 014030；2.新余學院 機電工程學院，江西 新余 338004)

0 引言

近年來，無人機在軍事、民用和商用領域得到了廣泛應用，逐漸成為航空飛行器領域的研究熱點[1-5]。其中，四旋翼無人飛行器更成為無人機研究的新寵，相對于直升機和固定翼飛機，具有體積小、質量輕、操控靈活等特點，可完成垂直起降、低空懸停、低速巡航等飛行動作，因此廣泛應用于軍事偵察、搶險救災、農林植保、航拍攝影等領域[6-9]。雖然四旋翼無人機具有很多優點，但它是一個欠驅動系統，只有4個控制輸入，卻有6個控制輸出，并且四旋翼系統還具有強非線性、強耦合、強時變性等特點，給飛行控制系統的設計帶來了巨大的挑戰[10-14]。

國內外很多學者應用線性、非線性及智能控制方法設計了四旋翼無人機控制系統。如Salih 等[15]用PID算法設計了飛行控制器；Besnard等[16]用滑模算法設計了抗干擾觀測器，用于抑制飛行中受到的外界干擾；Shirzadeh等[17]基于視覺方法為四旋翼無人機設計了一種神經網絡控制器；Erginer等[18]設計了混合模糊PID控制器，用以研究四旋翼無人機的時間延遲問題。這些研究成果使四旋翼的飛行控制系統有了一定改進。

但是，當四旋翼無人機用于執行某些特殊的飛行任務時，其自身參數(如自身質量)會產生較大變化，例如在執行噴灑農藥、播種、授粉、滅火等任務時，無人機自身質量會隨時間緩慢減小，且減小量可能會達到初始質量的2/3，從而給飛行控制帶來嚴重干擾。之前的研究大多沒有考慮四旋翼在這類情況下的應用，而是假設無人機質量為固定值，從而引入了較大的模型參數誤差，降低了控制器的穩定性，嚴重影響了無人機的飛行品質。

本文研究主要針對四旋翼無人機在有質量慢變情況下的應用，基于自適應控制理論設計質量觀測器來估計四旋翼的實時質量，并用估計值修正控制系統的質量參數。將質量觀測器與經典反步控制器(CBC)結合，并增加了第一類控制誤差的積分，提出了反步自適應控制器(BIAC)，用于無人機的飛行控制。仿真實驗結果表明：當無人機發生質量慢變或質量突變的情況時，BIAC都可以更好地估計四旋翼的實時質量，估計誤差為自身質量的5%～8%；ze軸的軌跡跟蹤誤差也大為減小，相對CBC，ze軸的跟蹤誤差減小80%左右。表明BIAC能夠更有效地對變質量四旋翼無人機進行實時控制，軌跡跟蹤精度明顯提高。

1 四旋翼無人機動力學模型

(1)

式中：R和N為轉換矩陣，

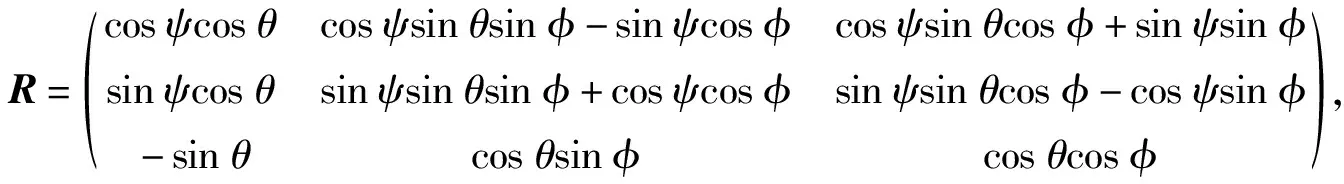
(2)

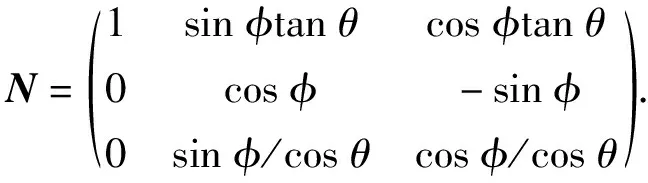
(3)

四旋翼無人機通過適當改變4個旋翼的轉速，產生φ、θ、ψ3種姿態角，并產生相應的運動，如圖1、圖2所示。圖1中，m為無人機質量，g為重力加速度，F1、F2、F3、F4分別為旋翼1、旋翼2、旋翼3、旋翼4的升力，ω1、ω2、ω3、ω4分別為旋翼1、旋翼2、旋翼3、旋翼4的轉速。

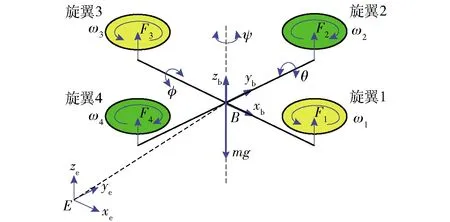
圖1 四旋翼無人機結構圖

圖2 四旋翼無人機運動示意圖

為了簡化動力學模型，便于求解計算，對四旋翼系統做出如下假設：

1)四旋翼無人機的機身是嚴格對稱的剛體。

2)無人機的幾何中心與質量中心重合。

3)忽略飛行中的槳葉揮舞和外部干擾。

利用牛頓定律和歐拉方程，可以得到四旋翼無人機動力學方程為

(4)

式中：Ff、Fd和Fg分別為平動力、平動空氣阻力和重力；I、Mf和Md分別為轉動慣量、轉動力矩和空氣阻力力矩向量。(1)式～(3)式代入(4)式，并考慮假設條件，可整理得到無人機非線性動力學模型如下：

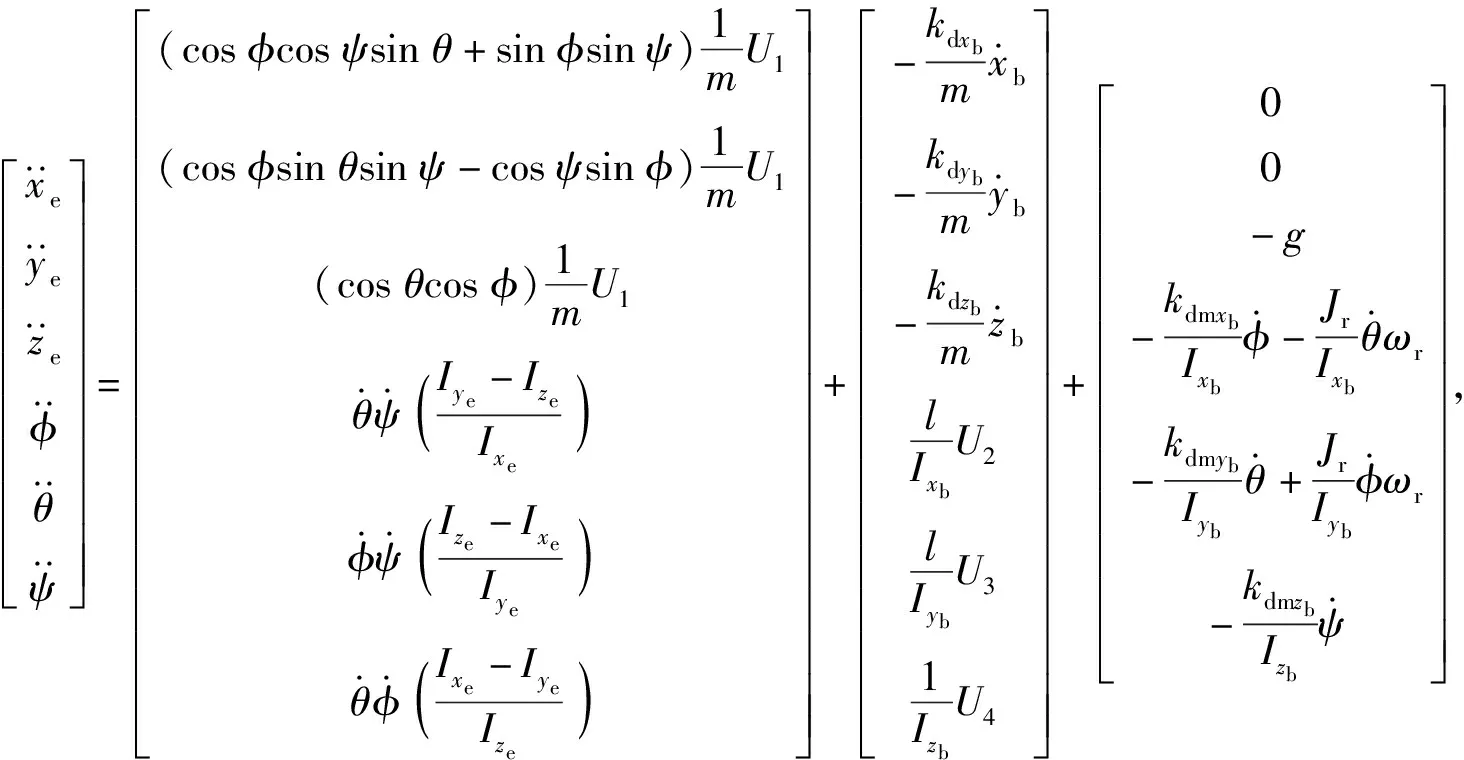
(5)

式中：Jr為電機轉動慣量；Ixb、Iyb、Izb分別為無人機繞xb、yb、zb軸的轉動慣量；kdxb、kdyb、kdzb分別為無人機沿xb、yb、zb軸的空氣阻力系數；l為旋翼中心到機體坐標系原點的距離；kdmxb、kdmyb、kdmzb分別為無人機沿xb、yb、zb軸的空氣阻力矩系數；Ui(i=1,2,3,4)為控制輸入，

(6)

b為U1、U2、U3與轉速之間的轉換系數，d為U4與轉速之間的轉換系數；ωr為電機轉速差值，

ωr=ω2+ω4-ω1-ω3.

(7)

定義控制輸入向量為

(8)

式中：uxe、uye為虛擬控制輸入。

2 CBC控制器設計

由于四旋翼無人機飛行速度較低，空氣阻力Fd和空氣阻力矩Md對模型精度的影響可忽略，在地球坐標系Exeyeze下建立四旋翼系統的非線性動力學方程為

(9)

式中：

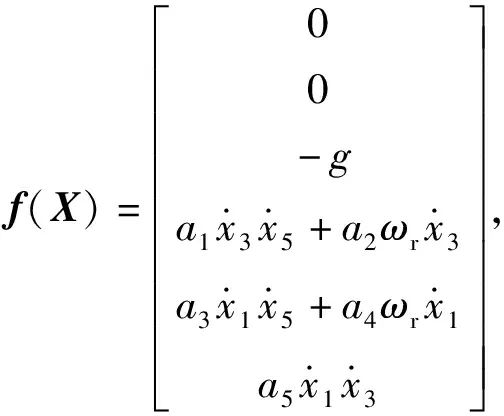
(10)

式中：

(11)

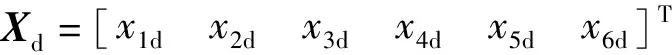
步驟1引入第一類跟蹤誤差向量

(12)

式中：e1、e3、e5、e7、e9、e11分別為x1、x2、x3、x4、x5、x6的第一類跟蹤誤差。

選擇Lyapunov函數為

(13)

對V1按時間求導，有

(14)

為穩定E1，引入函數

(15)

式中：K1為參數向量，K1=[k1k3k5k7k9k11]，k1、k3、k5、k7、k9、k11均為正常數。

(16)

步驟2引入第二類跟蹤誤差向量

[e2e4e6e8e10e12]T，

(17)

式中：e2、e4、e6、e8、e10、e12分別為xj,j=1,2,…,6的第二類跟蹤誤差。對E2按時間求導，有

(18)

選擇Lyapunov函數為

(19)

對V2按時間求導，有

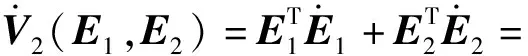
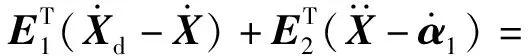
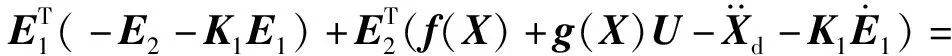
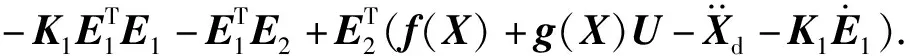
(20)

步驟3為了使E2穩定，選取控制律Uc為

(21)

式中：K2為參數向量，K2=[k2k4k6k8k10k12]，k2、k4、k6、k8、k10、k12均為正常數。用Uc代替(20)式中的U，則V2的導數可以改寫為

(22)

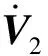
3 BIAC設計

對于存在質量慢變的四旋翼系統，基于自適應控制理論設計了質量觀測器，用于估計無人機的實時質量，并在反步控制方法基礎上增加第一類誤差的積分，設計BIAC。考慮系統質量僅與控制輸入uxe、uye和U1有關，因此質量觀測器僅作用于控制系統的位置控制器，如圖3所示。

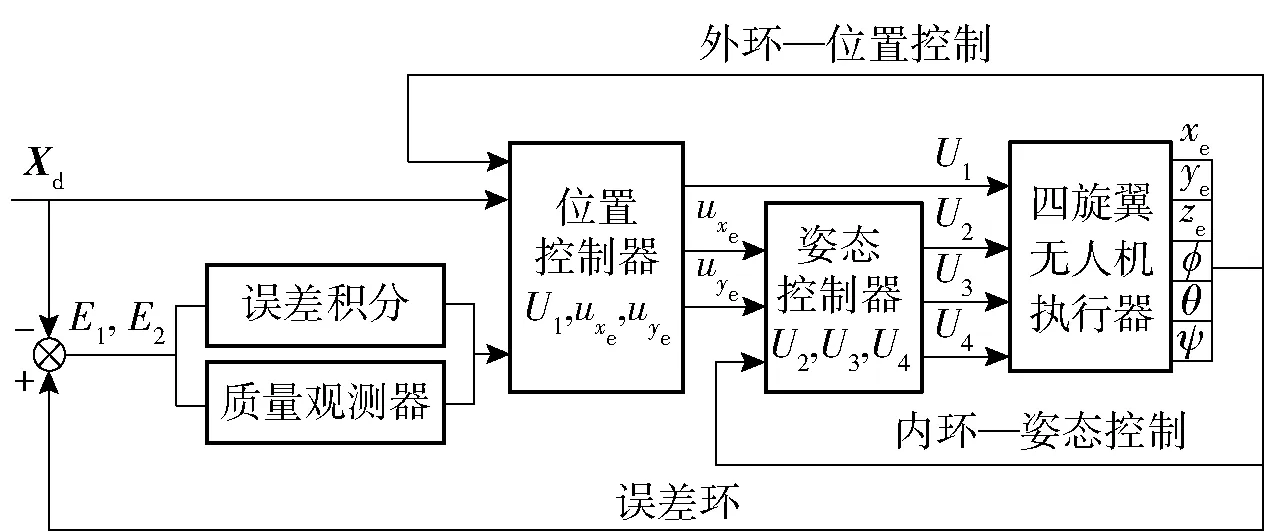
圖3 四旋翼無人機控制方案

BIAC的設計過程如下：

步驟1將(21)式中uxe、uye和U1的質量m替換為估計質量并引入誤差積分，可以得到

(23)

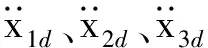
(24)

步驟2定義系統質量的觀測誤差為

mδ=m-.

(25)

由于系統質量緩慢變化，質量變化對時間的導數近似為0 kg/s，則mδ對時間求導，得

(26)

步驟3選擇新的Lyapunov函數為

(27)

式中：km為質量自適應參數。

V3對時間求導，得

(28)

步驟4令

(29)

為了使質量觀測誤差mδ收斂，令對時間的導數為

(30)

(31)

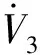
控制律(21)式中的位置控制律替換成(23)式，可以得到BIAC的控制律為

(32)

式中：P為誤差積分向量，P=[p1p3p50 0 0]T。

由此可得BIAC的姿態控制律為

(33)

4 仿真結果及分析

為了驗證BIAC對變質量四旋翼無人機的控制效果，在MATLAB/Simulink軟件環境下進行軌跡跟蹤的仿真實驗。期望軌跡為地球坐標系Exeyeze下Exeye平面的圓形軌跡，ze軸為固定高度2 m，期望軌跡表達式為

(34)

設置初始值xe0=4 m，ye0=6 m，ze0=2 m，仿真時間為20 s.系統的初始質量為0.65 kg，質量的變化量Δm=-0.02×t(kg)，t為仿真時間，施加外部周期干擾力fxe=fye=fze=0.2×Nsint.仿真結果如圖4和圖5所示，質量估計結果如圖6所示。

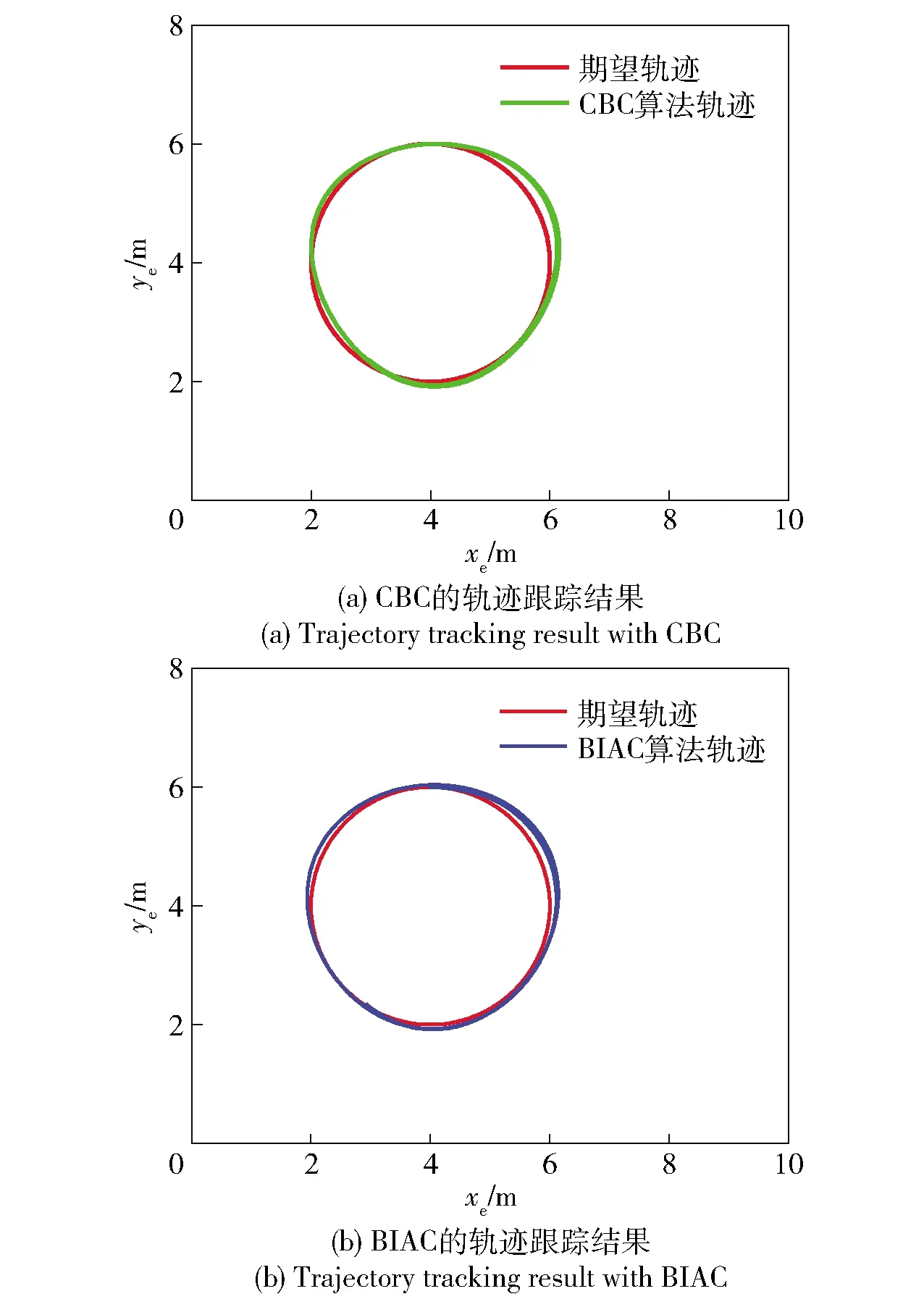
圖4 Exeye平面的軌跡跟蹤

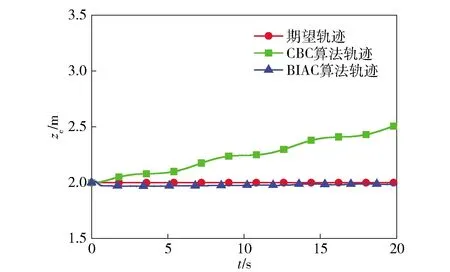
圖5 ze軸的軌跡跟蹤

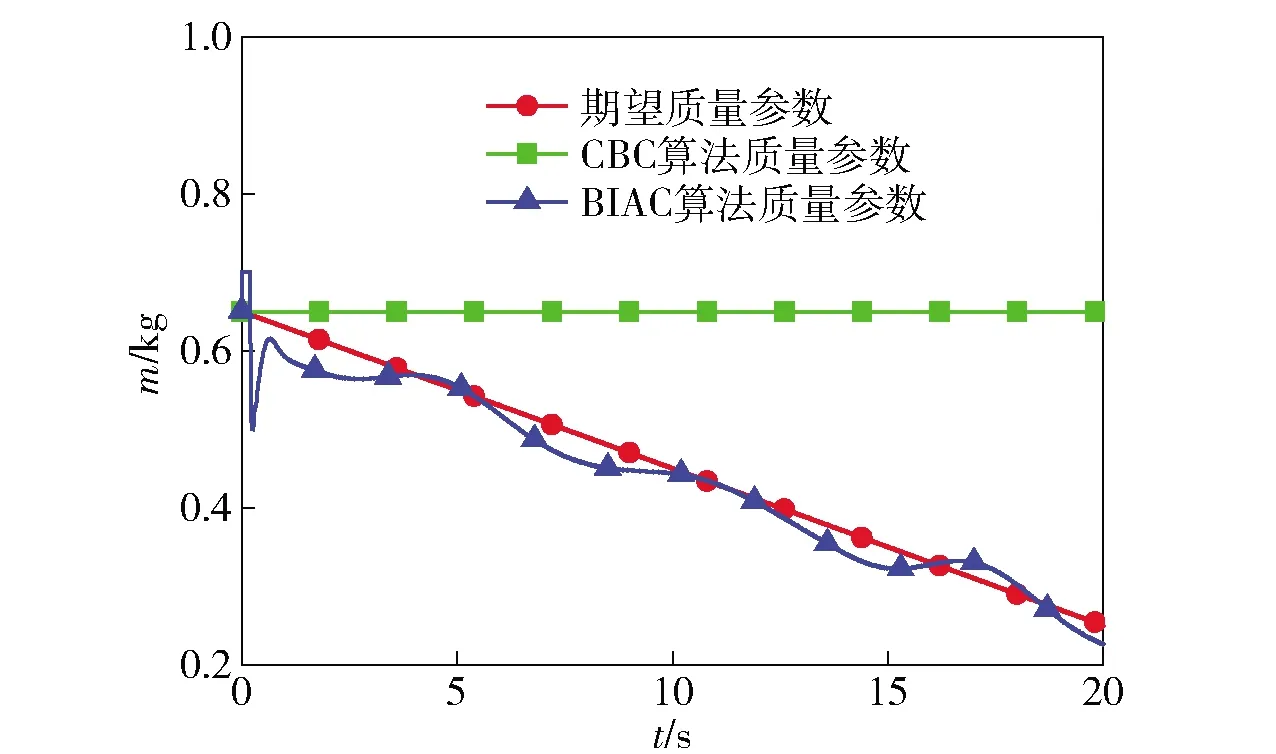
圖6 四旋翼無人機的實時質量

從圖4(a)、圖4(b)可以看出，在Exeye平面內，CBC和BIAC都可以使四旋翼無人機較好地跟蹤預定軌跡，可見無人機的質量變化對xe軸方向、ye軸方向的控制影響不大。由圖5可知，在ze軸方向，由于系統質量一直設置為初始值0.65，質量誤差隨時間累積，用CBC得到的跟蹤誤差逐漸增大；由于使用質量觀測器估計并修正了系統實時質量，BIAC的跟蹤誤差隨時間逐漸減小。在20 s內ze軸的平均跟蹤誤差，BIAC較CBC減小了89%.

從圖6中可以看出：用BIAC得到了系統質量估計值，在初始階段經歷了短暫的波動后，逐漸逼近系統的真實質量；受到外部周期干擾的影響，質量估計誤差也呈現出周期性振動，但振幅不大，表明在引入誤差積分后，質量觀測器的魯棒性得到了提高；20 s內系統質量估計的平均誤差，為系統自身質量的5.2%.

當無人機在仿真第5 s時產生質量突變，質量的變化量Δm=-0.3 kg，仍然對無人機施加外部周期干擾力fxe=fye=fze=0.2×Nsint，此時ze軸的軌跡跟蹤和無人機實時質量結果如圖7、圖8所示。由圖7可以看出：在無人機發生質量突變后，CBC控制律的位置誤差產生了突變，并且穩態誤差沒有隨時間減小，表明質量突變使控制精度大為降低；BIAC仍然能夠穩定地跟蹤ze軸軌跡，穩態跟蹤誤差沒有發生突變；20 s內BIAC的ze軸平均跟蹤誤差較CBC減小了71%.由圖8可以看出，BIAC得到了系統質量估計值收斂于系統的真實質量，20 s內質量估計的平均誤差，為系統自身質量的7.6%，最大超調量為29%.

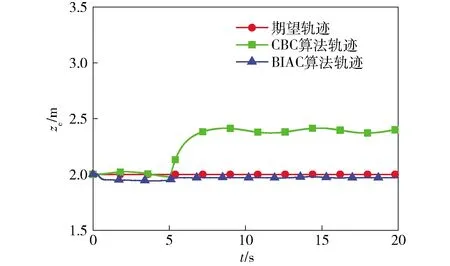
圖7 質量突變情況下ze軸軌跡跟蹤

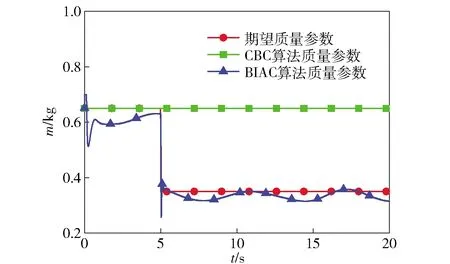
圖8 質量突變情況下四旋翼無人機的實時質量

5 結論

本文基于自適應控制理論設計了質量觀測器，用于估計四旋翼無人機的實時質量，與CBC相結合，并在位置控制器中增加了第一類控制誤差的積分，提出了BIAC，用于無人機的軌跡跟蹤控制。仿真實驗結果表明，質量觀測器可有效地估計無人機的實時質量，并有較強的魯棒性，通過實時修正質量參數降低了無人機ze軸的軌跡跟蹤誤差。因此，對于存在質量慢變或突變的四旋翼無人機系統，BIAC都能夠更好地完成軌跡跟蹤任務，跟蹤精度明顯優于CBC.

目前的研究只使用仿真方法對控制器進行了驗證，沒有對控制參數進行實際整定；在未來的工作中，將利用四旋翼無人機試驗平臺驗證并優化本文提出的控制算法。