球扁鋼的矯直角及軸向矯直解析模型

殷 璟，胡如夫，陳春梅

(寧波工程學院 機械工程學院，浙江 寧波 315336)

0 引言

球扁鋼是船舶專用結構型鋼，是建造航母、戰艦、貨輪、破冰船等大型船只所必需的重要龍骨鋼材[1]，其特點是截面不對稱使冷卻過程中溫度分布不均，從而造成嚴重的內應力彎曲，矯直前撓度通常超過30 mm/m，且在縱向和水平方向均有初始彎曲，如圖1所示。國標GB/T 9945—2012規定，球扁鋼的殘余撓度應小于3 mm/m，總撓度不大于總長度的0.3%，因此球扁鋼矯直時需在專用矯直機上，借助特殊形狀的矯直輥對兩個方向同時進行矯直。

圖1 矯直前的球扁鋼Fig. 1 Bulb-flat steel before straightening

球扁鋼因軋制過程中不一致的壓下率和冷卻過程中不均勻的溫度場致使彎曲問題嚴重[2-3]，研究人員立足于生產實踐，提出了一些解決該問題的方案。魏振洲等[4]提出采用雙根對稱軋制法，解決球扁鋼的軋制不對稱和冷卻不對稱問題，并給出了具體的孔型設計和軋制方案；吳維等[5]發現球扁鋼在軋制過程的扭轉變形與軋制壓下量和軋件長度有關，提出軋件長度取軋件原始厚度的10 倍進行軋制，能夠明顯減少球扁鋼的扭轉變形；李秋紅等[6]通過有限元法模擬了球扁鋼的冷卻過程，其截面溫度場分布說明冷卻不均是引起球扁鋼彎曲的主要原因，提出通過對球扁鋼進行軋前、軋后水冷的措施來解決該問題，并介紹了球扁鋼軋后水冷裝置的布置和設計；李建華等[7]提出終軋后設置噴霧嘴對內側表面進行強制冷卻以及增加冷床預彎功能，可有效提高球扁鋼的成材率。

從上述研究成果中可以發現，目前針對球扁鋼的大部分研究主要集中于對球扁鋼初始彎曲原因的分析及如何在軋制和冷卻過程中減小球扁鋼的初始彎曲。但在球扁鋼的生產過程中，軋制和冷卻的不均勻、不對稱是不可避免的，即使通過多種途徑減小球扁鋼的初始彎曲，仍需多輥矯直機矯直才能達到其平直度要求。在球扁鋼的矯直過程中，最重要的是矯直角和軸向矯直規程的制定，但由于球扁鋼的截面形狀完全非對稱，使其矯直工藝的理論研究較為困難[8-9]，生產中工藝規程的制定主要依賴技術人員的經驗，調試成本高、周期長。因此，建立一種球扁鋼軸向矯直解析模型為其矯直角和軸向矯直規程的制定提供理論依據，從而提高球扁鋼的矯直效率和矯直精度十分必要。

1 球扁鋼的雙向同矯工藝

球扁鋼初始彎曲的特點是縱向為“波浪彎”，軸向為“鐮刀彎”，生產中球扁鋼采用雙向同矯的方式，即：縱向連續往復彎曲矯直，軸向單向反彎曲矯直。因此球扁鋼矯直機與普通矯直機略有不同。首先，球扁鋼矯直機的矯直輥為圓錐形，使球扁鋼矯直時與水平面呈一定角度，有利于減小軸向矯直力，同時可提高矯直輥的通用性，降低了換輥成本；其次，為滿足球扁鋼雙向同矯的要求，球扁鋼矯直機的下排輥軸向可調，上排輥縱向和軸向均可調。當球扁鋼傾斜進入矯直機后，上排矯直輥的縱向壓下使球扁鋼發生連續往復彎曲變形，以矯直其z向初始撓度；將各矯直輥的軸向位置調整成一條與球扁鋼軸向初始撓度方向相反的反彎曲線，使球扁鋼發生單向反彎曲變形，以矯直其y向初始撓度。球扁鋼的雙向同矯工藝如圖2所示。

圖2 球扁鋼雙向同矯工藝示意圖Fig. 2 Diagram of double-direction straightening for bulb-flat steel

在實際生產中發現，球扁鋼的縱向初始彎曲率并不大，部分規格的球扁鋼在軋制冷卻后，其z向初始撓度甚至是滿足國標中對平直度要求的，因此球扁鋼的矯直重點是軸向(即y向)大初始曲率彎曲，其關鍵參數是矯直角和軸向矯直規程。

2 球扁鋼截面簡化及參數化

球扁鋼截面如圖3所示，其截面參數分別為：高度h，寬度b，腹板厚度t1，球頂面與腹板間的圓角半徑、球端圓角半徑r1，腹板端部圓角半徑r，重心距離dx。

為便于分析計算，球扁鋼截面按以下方式簡化：球扁鋼腹板端部圓角半徑r很小，忽略不計后簡化為直角；球端圓弧部分簡化為與原弧面相切的直線，寬度為t2；球頂面與腹板間的球端圓弧，簡化為直線相交。簡化后的球扁鋼截面如圖3中虛線所示。通過數學方法可證明，球頂寬度t2與球頭圓角半徑r1有如下關系：

圖3 球扁鋼截面參數Fig. 3 Sectional parameters of bulb-flat steel

為檢驗截面簡化對截面屬性的影響程度，以截面面積A和重心距離dx作為截面簡化前后的對比參數，對比范圍是國標GB/T 9945—2012列出的全部54個規格的球扁鋼，對比結果如圖4所示。

圖4 球扁鋼截面簡化前后參數對比Fig. 4 Comparison of parameters before and after section simplification for bulb-flat steel

數據顯示，簡化后面積相對偏差的最大值為1.304%，平均值為0.656%；重心距離相對偏差的最大值為0.621%，平均值為0.404%。因此，簡化后的球扁鋼截面特征和參數可以較為準確地反映原截面的幾何特征，由截面簡化引入的計算誤差較小。

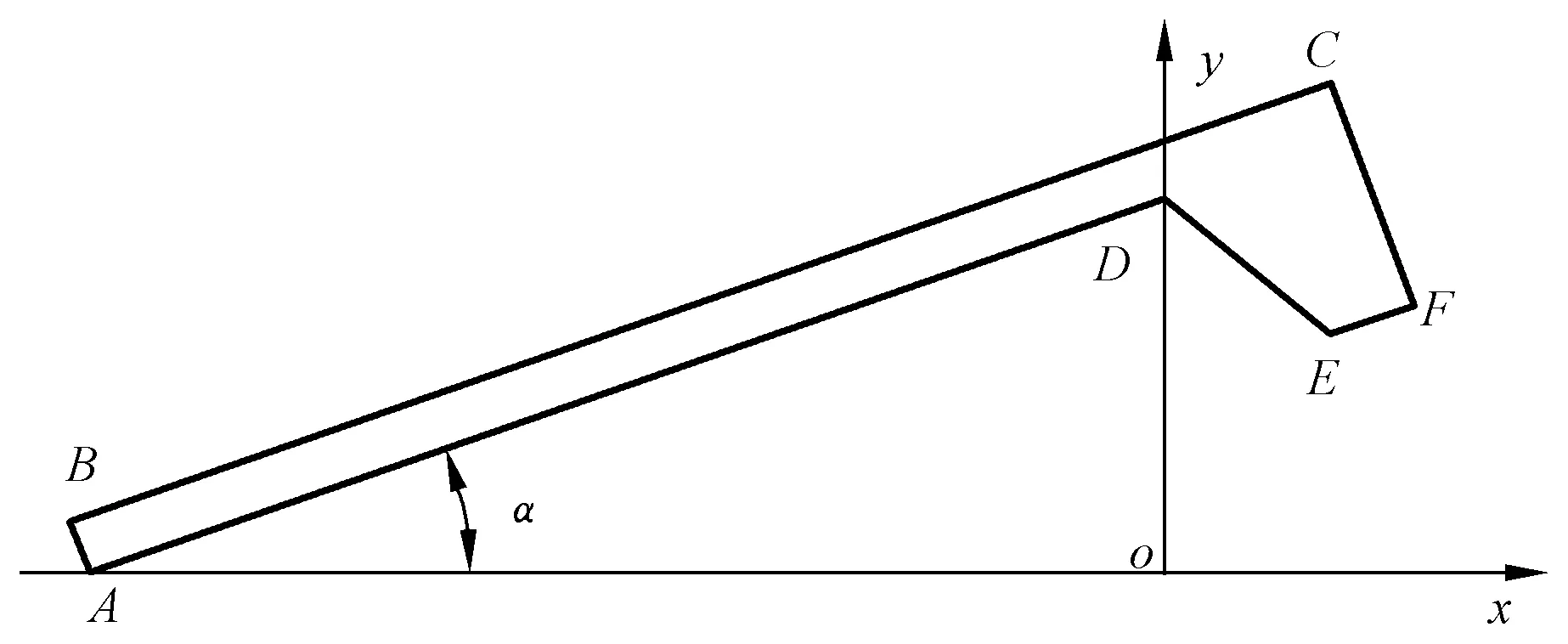
圖5 球扁鋼截面參數化Fig. 5 Section parameterization of bulb-flat steel

(1)

(2)

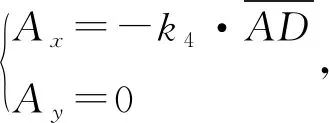
lAB：y=k3(x-Ax)，

lBC：y=k1(x-Bx)+By，

lCF：y=k3(x-Cx)+Cy，

lDE：y=k2·x+Dy，

lEF：y=k1(x-Ex)+Ey。

3 球扁鋼的矯直角

出于矯直工藝的考慮，球扁鋼矯直時，腹板與水平方向呈一定夾角，即矯直角。如圖6所示，當球扁鋼自然朝下放置時，腹板與水平方向的夾角是最小矯直角，用αmin表示。根據幾何關系，有

圖6 球扁鋼最小矯直角Fig. 6 The minimum straightening angle of bulb-flat steel

(3)

αmin=arccos(cosαmin)。 (4)

由式(4)計算出全部國標規格球扁鋼最小矯直角αmin的范圍是8.23°～10.75°。而球扁鋼矯直角的確定還要綜合考慮其對矯直力和矯直質量的影響。通過計算發現，當矯直角為20°時，球扁鋼截面對縱向形心線的慣性矩比腹板平放時小6%左右，這就意味著矯直角使軸向矯直力減小，且矯直角越大，軸向力就越小。通常，球扁鋼矯直機設計的最大軸向載荷是縱向最大載荷的60%左右，因此減小軸向矯直力對矯直機有利。從矯直質量方面考慮，當有一定矯直角時，縱向的多輥矯直過程會對側彎有輔助矯直的作用，矯直角越大，側彎的縱向分量越大，矯直效果越好。但矯直角不能過大，因為矯直角增大雖然會減小軸向矯直力，但會相應增加縱向矯直力，且縱向矯直力增加的絕對值大于軸向矯直力減小的絕對值。另外，過大的矯直角會使球扁鋼進入矯直機時咬入困難，從而降低矯直速度，增加“擺尾”隱患。綜合考慮，矯直角在15°～25°較為合適。南鋼集團無錫金鑫軋鋼有限公司在生產中大型規格球扁鋼時均采用20°的矯直角。

值得注意的是，球扁鋼軋制時為保證其斷面形狀的正確和提高軋輥重車次數，采用孔型的斜配角度。對于球頭部開口的孔型，斜配角取10°～15°；對于蝶式孔型，斜配角取15°～16°[10]。球扁鋼的矯直角與軋制時的斜配角接近或是出于相似的考慮，既能使矯直輥受力均衡，也能增加矯直輥的重車次數。

4 球扁鋼軸向矯直解析模型

4.1 球扁鋼軸向純彎曲回彈分析

球扁鋼的軸向矯直可視為完全非對稱截面曲梁的單向反彎曲。完全非對稱截面曲梁彎曲時應變中性層和幾何中心層不重合，按經典彎曲彈復理論很難建立準確的彈復方程，矯直角的加入使彎曲回彈后曲率的計算更為困難。而小曲率平面彎曲彈復理論[11]的建立為該類工程問題的理論分析提供了可靠的分析方法和統一的彈復方程，并已在單向非對稱截面曲梁的彎曲回彈分析中得到了應用與驗證[12]。本文也將繼續采用小曲率平面彎曲彈復理論分析球扁鋼矯直時的彎曲回彈。

設球扁鋼軸向的初始曲率半徑是ρ0x，軸向反彎曲率半徑是ρx，在xoy坐標系下，球扁鋼幾何中心層橫坐標為xc，當量應變中性層的橫坐標為x0，真實應變中性層的橫坐標為xt，軸向初始曲率為K0x，軸向彎曲曲率為Kx，軸向當量應變中性層曲率為Kεx。由小曲率平面彎曲彈復理論，軸向反彎時的真實應變εx可表示為

εx=(x-xc)(Kεx-K0x)-(Kεx/Kx-1)=
K0x(xc-x)-Kεx(x0-x),

式中，

Kx=1/ρx，

(5)

Kεx=1/[ρx-(x0-xc)]，

(6)

K0x=-1/ρ0x。

當x=xt時，真實應變εx=0，即

K0x(xc-xt)-Kεx(x0-xt)=0，

則

xt=(K0x·xc-Kεx·x0)/(K0x-Kεx)。

(7)

設球扁鋼的材料性能符合簡單隨動強化材料模型[12]，ex為軸向彈性區高度，則其彈性應變εe可表示為

εe=K0x(xc-xt-ex)-Kεx(x0-xt-ex)=σs/E,

式中,σs為屈服應力，E為彈性模量，由此可推出

ex=σs/[E(Kεx-K0x)]，

(8)

則純彎曲時球扁鋼的截面應力可表示為

式中，D為塑性切線模量，σ0=(1-D/E)σs。

球扁鋼軸向純彎曲時的真實應力和真實應變如圖7所示。

圖7 球扁鋼軸向純彎曲應變、應力示意圖Fig. 7 Schematic diagram of strain and stress for bulb-flat steel axial pure bending

由圖7可知，球扁鋼截面的不對稱造成其純彎曲時受拉和受壓的部分也不對稱，但其截面軸向受力仍然滿足力平衡方程，即

Fx1=-Fx2，

式中,Fx1是真實應變中性層xt右側應力對相應面積的積分，Fx2是真實應變中性層xt左側應力對相應面積的積分。

顯然，用解析法求解真實應變中性層xt和當量應變中性層x0的位置是非常困難的，但借助力平衡方程和數值積分法可以較為準確地求解出這兩個關鍵參數，具體求解思路如下：

1)由截面形狀可以判斷x0≥xc，因此給x0賦初值x0=xc。

2)初始曲率K0x、彎曲曲率Kx均為已知量，由x0的初值可求出當量應變中性層曲率Kεx的初值，繼而求出xt和ex的初值。

3)由xt的位置和ex的大小確定應力彈性區和塑性區所對應的面積范圍。

4)用數值積分法求解Fx1和Fx2。

5)判斷ΔFx=|Fx1+Fx2|是否大于允差ζ，程序中設定ζ=100 N。

6)如ΔFx>ζ，則給x0賦新值x0=x0+0.01(0.01是迭代步長)，程序回到第(2)步進行循環。

7)如ΔFx≤ζ，則認為x0的賦值使力平衡方程成立，將其代入式(7)和式(8)可求出xt和ex，圖7中應力和應變的分布被確定。

8)由小曲率平面彎曲彈復理論可知，球扁鋼軸向純彎曲彈復后的曲率Kpx為

(9)

9)球扁鋼軸向最大矯直力Fx可表示為

(10)

式中，n是矯直輥個數，L是輥距。將球扁鋼純彎曲時的彎矩Mx和矯直機設備參數代入式(10)，即可求得球扁鋼軸向最大矯直力Fx。

借助MATLAB軟件對上述分析計算過程進行編程，輸入球扁鋼截面的基本參數h、b、t1和r1以及初始曲率、彎曲曲率，即可計算出球扁鋼彎曲回彈后的曲率，計算結果如圖8所示。通過大量的分析計算發現，彎曲變形越大，當量應變中性層和真實應變中性層偏離幾何中心層越遠。

圖8 球扁鋼軸向彎曲程序運行結果Fig. 8 Program result of axial bending for bulb-flat steel

4.2 球扁鋼軸向矯直解析模型的驗證

為驗證球扁鋼軸向矯直解析模型的可靠性，在南鋼集團無錫金鑫軋鋼有限公司的8輥球扁鋼矯直機上對430×20和260×10兩種典型規格的球扁鋼進行了軸向矯直實驗。該矯直機的輥距L為1 m，矯直角為20°。球扁鋼的材料性能參數如表1所示。

表1 球扁鋼的材料性能Tab.1 Material properties of bulb-flat steel

430×20規格球扁鋼的軋制長度為50 m，最大初始撓度達2.5 m/50 m，即初始曲率K0=7.92×10-3m-1，換算后軸向初始曲率K0x=K0cosα=7.44×10-3m-1。通過程序試算后確定，當軸向彎曲曲率Kx達到11.26×10-3m-1時，彎曲回彈后的曲率Kpx為0.271×10-3m-1，即矯后殘余撓度為0.084 m/50 m，可達到國標要求。由輥距和輥數可反推出當軸向矯直規程為[0,8.5,14,17,17,14,8.5,0]mm時軸向彎曲曲率Kx為11.26×10-3m-1。將該軸向矯直規程輸入球扁鋼矯直機的控制系統進行矯直實驗，經測量，球扁鋼矯后殘余撓度為0.102 m/50 m，與理論計算值較為吻合，另外實測的最大矯直力為531 kN，亦與理論計算的517 kN較為接近。

260×10規格球扁鋼的軋制長度也是50 m，最大初始撓度為1 m/50 m，即初始曲率K0=3.20×10-3m-1，換算后軸向初始曲率K0x=K0cosα=3.01×10-3m-1。通過程序試算后確定，當軸向彎曲曲率Kx達到15.92×10-3m-1時，彎曲回彈后的曲率Kpx為0.025×10-3m-1，即矯后殘余撓度為0.007 8 m/50 m，遠小于國標要求。但在反推軸向矯直規程時發現，當軸向彎曲曲率較大時，中間幾個矯直輥的軸向調整量會超過矯直機的設計標準，因此選擇前6個矯直輥形成反彎曲線，后兩個矯直輥的軸向調整量逐步過渡，便于球扁鋼的導出，最終確定軸向矯直規程為[0,7.3,11,11,7.3,0,8.3,11]mm。將該軸向矯直規程輸入球扁鋼矯直機的控制系統進行矯直實驗，經測量，球扁鋼矯后殘余撓度為0.065 m/50 m，達到了國標的矯直要求，實測最大矯直力為102 kN，比理論計算的86 kN大15.7%。

矯直實驗結果說明，利用球扁鋼軸向矯直解析模型可以較為準確地預測出矯直所需的軸向彎曲曲率和矯直時的最大軸向力，進而反推出軸向矯直規程，可大大縮短球扁鋼矯直的調試時間。

5 結論

本文建立了精確的球扁鋼幾何參數化模型，基于該模型計算出全部國標規格球扁鋼最小矯直角αmin的范圍是8.23°～10.75°。增大矯直角可減小軸向矯直力，并能增大側彎的縱向分量，提高矯直效果；但過大的矯直角會使縱向矯直力大幅增加，同時增加了球扁鋼進入矯直機時的咬入困難，降低矯直速度，增加“擺尾”隱患。綜合考慮矯直力、矯直質量和咬入條件等多種因素，球扁鋼的矯直角應在15°～25°。在此基礎上，本文借助小曲率平面彎曲彈復理論，建立了球扁鋼軸向矯直解析模型。該模型通過引入當量應變和當量應變中性層的概念，解決了非對稱截面曲梁純彎曲時真實應變中性層和幾何中心層不重合的問題，實現了球扁鋼曲梁純彎曲回彈曲率的精確計算。現場矯直實驗結果表明，球扁鋼軸向矯直解析模型可準確預測球扁鋼軸向矯直彎曲曲率和最大矯直力，為球扁鋼軸向矯直規程的制定提供了理論依據。