基于三線陣CCD的室內導航方法研究

王 闖，屠曉偉

(1.上海大學 機電工程與自動化學院，上海 200444；2.許昌學院 信息工程學院，河南 許昌 461000)

0 引言

室內移動智能體廣泛應用在商業、物流、自動化生產、軍事等領域。移動智能體的高精度位置和姿態信息是完成用戶指定運行任務的基礎，同時也是實現精準運動控制和導航路徑規劃的前提條件。

室內移動智能體位置和姿態的測量方法主要分為兩類：相對定位和絕對定位[1]。相對定位技術通過估測移動智能體相對于起始位置的方向和距離來推斷出當前的位置信息。航跡推算法是相對定位技術中的一種經典方法，通過慣性測量單元或測量里程計的方法而實現的航跡推算法既不需要外部信息,也不需要向外發射任何信息，它能夠獨立工作并且連續不斷地為移動智能體提供定位服務。然而，航跡推算法的測量誤差會隨著時間積累，所以該方法僅滿足短時間內的狀態估計，無法實現復雜環境下的長時間定位[2]。同時航跡推算法還需要引入初始航向角與位置信息，在實際場景中較難實現。因此，移動智能體位置和姿態的估測更多地依靠絕對定位方法。

在過去幾十年，絕對定位受到相關研究者的關注，并取得了重大進展。絕對定位需要測量多個已知位置的參考點來獲取移動智能體的位置信息。室外絕對定位技術的典型代表是全球定位系統(Global Positioning System,GPS)，自從GPS投入使用后，室外定位的應用越來越廣泛。然而，在城市地區和建筑物內部，建筑物的墻壁和屋頂阻擋了GPS信號傳播，使得GPS系統不能在室內正常工作，因此室內絕對定位方法的研究進入了一個快速發展的時期[3]。

在室內絕對定位技術中，基于錨節點的測量方法為室內移動智能體的定位和導航提供了多種選擇，例如使用可見光[4]、超聲波[5]、Wi-Fi[6]、Ultra Wide Band (UWB)[7]等無線定位技術。然而，這些定位技術往往受到多徑效應等因素的干擾，而且絕大多數都不能提供三維的位置和姿態服務，在室內移動智能體的導航應用中存在很大的缺陷。

最近幾十年來，光電測量技術發展迅速，相關研究者提出了很多可行的方法。激光雷達主要采用紅外激光束以徑向視野掃描周圍環境，它以其測量精度高、靈活性強、實時性好等特點，已在多種室內環境場合中廣泛使用[8]。但是在某些場合下，如在飛機大部件的高精度裝配和對接程序中，激光雷達技術很難同時獲得移動平臺的位置和方向[9]。文獻[10]采用基于激光的光電掃描方式測量錨節點的三維坐標，并使用坐標轉換算法實現了室內位置和姿態的測量。但該方法需要使用復雜的旋轉激光掃描儀器測量室內錨節點的三維坐標，并且激光設備價格昂貴，不便于在室內多個移動智能體情況下大規模使用。

基于電荷耦合器件(CCD)或CMOS的視覺傳感器采用非接觸的測量方法，可以在不干擾系統的情況下估測出室內移動物體運動參數。視覺傳感器具有結構簡單、安裝方式多元化、探測信息豐富、自身不受外界電磁干擾等優點。文獻[11]使用面陣CCD相機來估測室內位置和姿態，但該方案需要分別考慮二維或三維工作情況，從而決定錨節點的使用個數。文獻[12]使用面陣相機觀測矩形約束信標，然后獲得機器人位置和姿態。然而，該系統要求相機的光軸總是指向目標中心點，這使得該方法復雜而笨拙，不適合室內較大工作范圍的使用。目前有一些商業現成的設備通過計算機視覺的方法來測量目標的位置和姿態信息[13]，但是這種設備不能提供360°方向的測量，不適合不斷變化的室內背景，并且這些設備價格昂貴，更大的測量空間需要更多的相機測量設備，導致整個系統成本開銷的增加。

現有的室內位置和姿態的視覺測量方法主要采用面陣CCD或CMOS，較少采用線陣CCD來實現室內移動智能體的位置和姿態的測量。文獻[14]使用線陣CCD測量室內移動物體的位置和姿態，然而該方法需要使用多套線陣CCD測量設備，并且只能在較小的室內空間測量位置和姿態。文獻[15]提出了一種3D運動跟蹤系統，該系統使用多個線性光學傳感器陣列，輔以慣性測量單元，在位置和姿態跟蹤方面取得了良好的性能。但是該方法需要使用線陣CCD和慣性測量單元分別測量位置和姿態，并且也只能在小范圍的室內空間內實現位置和姿態測量。

針對移動智能體在室內導航過程中的位置和姿態問題，本文使用3個線陣CCD和3個柱面透鏡設計了一種新型的室內位置姿態傳感器，通過三平面相交于空間一點的方法，即可在該傳感器上建立傳感器坐標系。通過在室內屋頂上布置多個紅外LED錨節點，根據位置姿態傳感器在室內移動的位置，測量傳感器視域范圍內錨節點的三維坐標值，獲取到至少3個錨節點在傳感器坐標系下的三維坐標值后，通過羅德里格矩陣坐標轉換算法，即可估測出移動智能體在室內的位置和姿態信息。該方法簡單實用，精度高，成本低，適合于室內移動智能體的大規模應用。

1 測量原理

線陣CCD在計算機視覺測量中應用廣泛，與面陣CCD或CMOS相比，線陣CCD具有高分辨率和快速的幀速率，在精確坐標測量和動態位置跟蹤方面具有突出的優勢[16]。

1.1 系統組成和工作原理

一維線陣相機由兩個部分組成，一個線陣CCD和一個柱面透鏡。柱面透鏡用于實現從三維空間到一維成像的投影映射。根據光學的基本原理，來自柱面透鏡一側物點的光線將在另一側形成線性圖像[17]，如圖1所示。

圖1 一維成像單元投影模型Fig.1 Projection model of the one-dimentional imaging unit

在圖1中，線陣CCD和柱面透鏡構成一維成像單元(One Dimensional Imaging Unit,ODIU)，來自LED發光點的光線通過柱面透鏡將聚焦在焦平面上。為了檢測由于LED發光點移動而引起的變化，將線陣CCD圖像傳感器放置在柱面透鏡的焦平面。線陣CCD垂直于柱面透鏡的光軸放置，用來檢測和標記LED移動時投影線的變化。線陣CCD的中心與柱面透鏡光軸的中心上下對照，它們之間的距離是柱面透鏡的焦距。LED的投影線垂直于線陣CCD并在CCD上形成脈沖峰值點，經過圖像處理后可計算出LED的一維圖像坐標。如果線陣CCD上的成像點和柱面透鏡的光軸是已知的，則可以計算出包含LED位置的平面。

一條直線和一個不在這條線上的點可以定義一個平面。為了在傳感器坐標系下測量LED錨節點的三維坐標，至少需要3個ODIU來存儲LED的3個一維圖像位置坐標，以重建傳感器坐標系下LED的坐標值。如圖2所示，3個ODIU的線陣CCD在同一水平面布置，LED的三維坐標可以通過3個平面的相交點來估測。當LED位于傳感器的視域范圍時候，LED穿過相應的柱面透鏡并形成分別垂直于3個線陣CCD的3條投影線，投影線在相應的焦平面上與3個線陣CCD相交形成3個投影點，以此來計算投影線的位置信息。如果確定了每個ODIU中的投影線的交點位置，則就確定了3個投影面，這3個投影面的相交點就是LED錨節點在傳感器坐標系的位置。因此，在傳感器坐標系下的LED錨節點的三維坐標可以由3個虛擬平面唯一地解析。

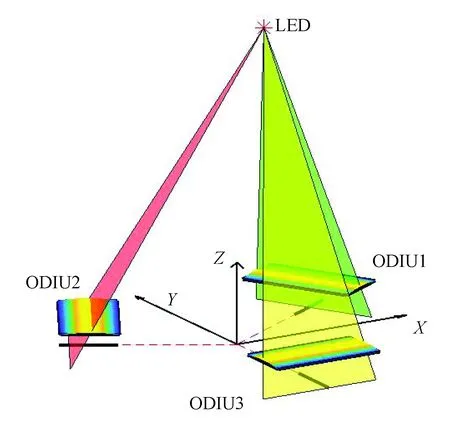
圖2 位置姿態傳感器原理圖Fig.2 Schematic of the position and attitude sensor

同時，將3個線陣CCD感光區域的延長線交點設置為位置姿態傳感器坐標系的原點，每個線陣CCD的感光區域都位于傳感器坐標系的XY平面上。其中線陣CCD3位于Y軸的負半軸上，而CCD1和CCD2分別位于第一象限和第二象限。

1.2 位置姿態傳感器視域

圖2中的位置姿態傳感器只能測量其視域范圍內LED錨節點的三維坐標。同時在室內導航中，傳感器的視域對于天花板上的錨節點布局非常重要，傳感器坐標系在XY平面上的投影圖如圖3所示。

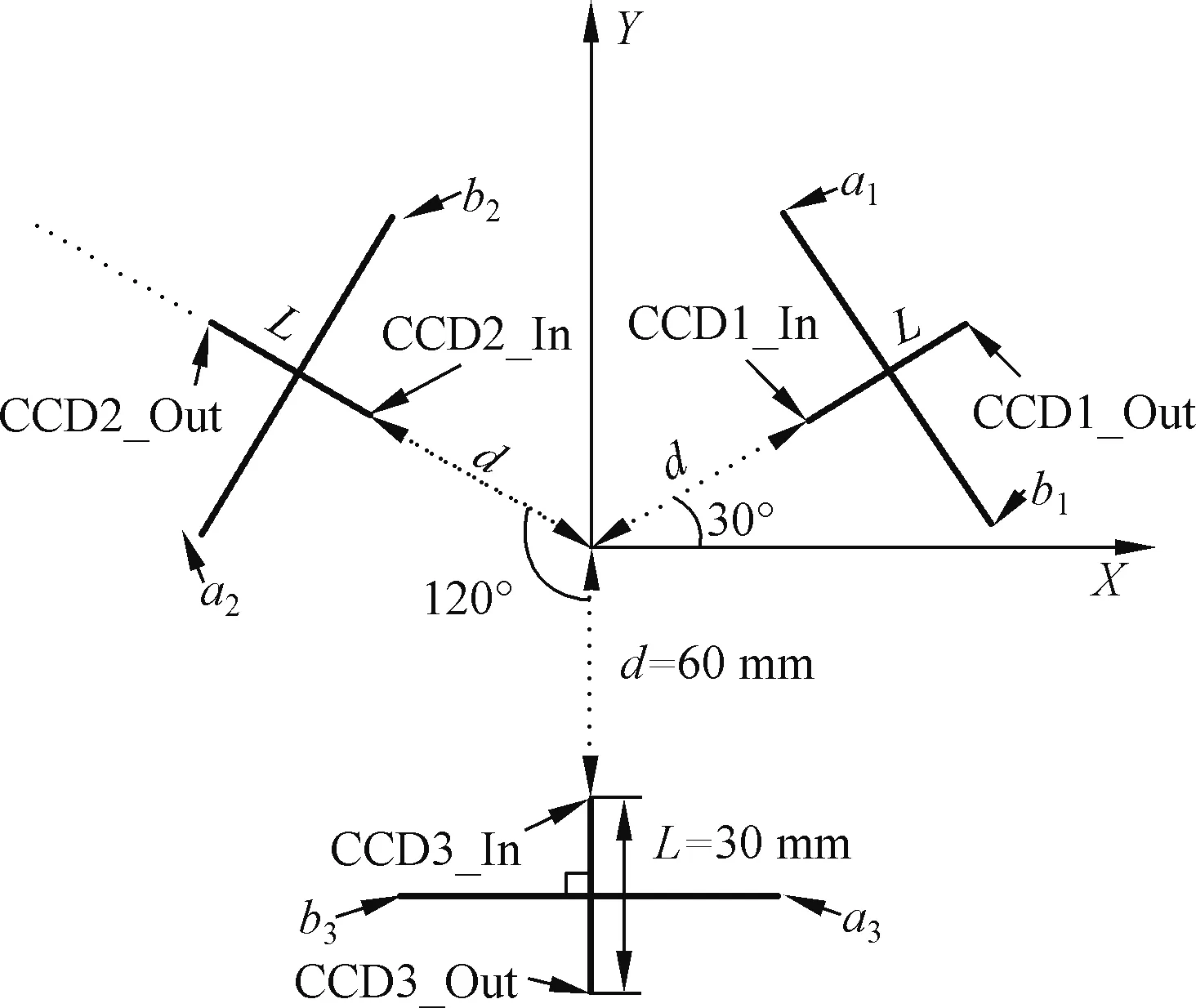
圖3 傳感器在XY平面投影圖Fig.3 Projection drawing of the sensor on XY plane

在圖3中，線陣CCD光敏元件的感光長度L都等于30 mm。線陣CCD3位于Y軸的負半軸上，將CCD3順時針旋轉120°移動到CCD2的位置，同時將CCD3逆時針旋轉120°移動到CCD1的位置。CCD1_In，CCD2_In和CCD3_In是線陣CCD靠近坐標原點的內邊緣，它們到原點的距離d都等于60 mm；CCD1_Out，CCD2_Out，CCD3_Out是線陣CCD的外邊緣，它們到原點的距離都等于90 mm。a1和b1，a2和b2，a3和b3分別是3個柱面透鏡的光軸在XY平面上的投影線，柱面透鏡的焦距為50 mm，仿真參數如表1所示。

根據表1，在3個線陣CCD的光敏區域每隔1 mm選擇投影點，由于一般室內距離大部分在6 m以內，因此只考慮室內空間的Z坐標值在[0,6 000 mm]范圍的情況。圖4是根據表1中的參數仿真得到的傳感器的視域圖。根據圖4中的仿真結果，傳感器最近的測量距離為300 mm，同時可測量視域隨著距離的增加而變大。

表1 仿真參數Tab.1 Simulation parameters

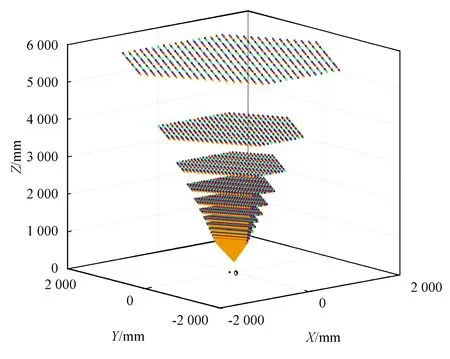
圖4 傳感器視域圖Fig.4 The vision field of the sensor

2 位置和姿態測量算法

在室內位置和姿態測量系統中，有兩個不同的坐標系統。一個是室內坐標系，它的坐標原點設在屋內的墻角處。另一個是位置姿態傳感器坐標系，它的坐標原點設定在傳感器上，如圖2所示。

2.1 數學模型

設定3個錨節點A1，A2，A3固定在天花板上，它們在室內坐標系下的坐標分別為A1(X1,Y1,Z1)，A2(X2,Y2,Z2)和A3(X3,Y3,Z3)。同時設定這3個錨節點在傳感器坐標系下的坐標值分別為C1(xc1,yc1,zc1),C2(xc2,yc2,zc2)和C2(xc2,yc2,zc2)，根據錨節點在室內坐標系和傳感器坐標系下的三維坐標值，列出坐標轉換方程來實現從傳感器坐標系到室內坐標系的轉換，即

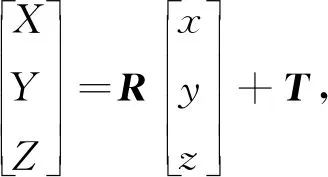
(1)

式(1)建立了錨節點在兩個坐標系之間的關系，其中[XYZ]T表示錨節點在室內坐標系下的坐標值，[xyz]T表示錨節點在傳感器坐標系下的坐標值，R是3×3旋轉矩陣，T=[x0y0z0]T是平移向量。在坐標轉換方程中，平移向量T表示傳感器坐標系的原點在室內坐標系的位置，旋轉矩陣R里面含有傳感器坐標系相對于室內坐標系的旋轉角度，這些旋轉角就是要求的姿態角。

假設傳感器坐標系的x軸，y軸和z軸在室內坐標系下的旋轉角分別是α、β和γ。設定α為俯仰角，β為滾轉角，γ為偏航角。同時定義順時針方向的旋轉角為正，逆時針方向的旋轉角為負。根據旋轉角，可以得到繞x軸，y軸和z軸轉動的旋轉矩陣為

定義旋轉矩陣R=Ry(β)Rx(α)Rz(γ)，其中α=arcsin(R[2,3]),β=-arctan(R[1,3]/R[3,3]),γ=-arctan(R[2,1]/R[2,2]),R的計算結果為

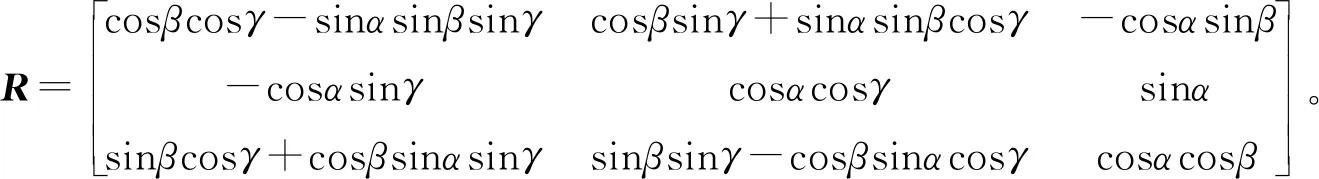
2.2 羅德里格矩陣坐標轉換算法

為了求解式(1)中T和R，至少需要3個錨節點。使用羅德里格矩陣坐標轉換算法來求解R和T。在式(1)中，根據轉換算法，首先要計算R，然后計算T[18]。

設反對稱矩陣S為

(2)

其中，a、b、c是獨立參數，R由反對稱矩陣S和3×3單位矩陣I組成，即

R=(I-S)-1(I+S)

。

(3)

由式(1)可以列出3個方程，第j個錨節點的方程分別減去第i個錨節點的方程，可以消除平移向量，然后得到

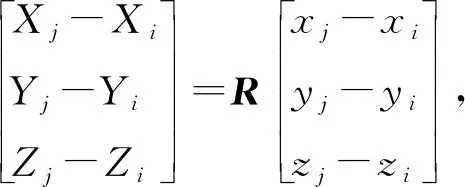
(4)

把式(3)代入(4)，可得到

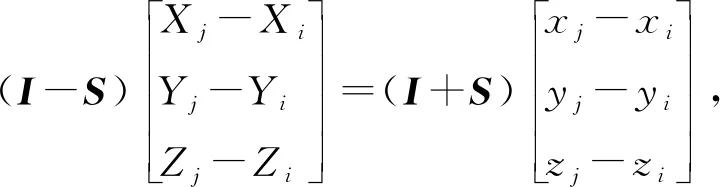
(5)

將式(2)代入式(5)，然后提取a，b和c并表示成

(6)

其中,Xij=Xj-Xi,Yij=Yj-Yi,Zij=Zj-Zi,xij=xj-xi,yij=yj-yi,zij=zj-zi。

在式(6)中，左邊的系數矩陣是一個奇異矩陣，在只有兩個獨立方程的情況下不能求解a、b和c這3個參數，再使用錨節點k和錨節點i可以得到

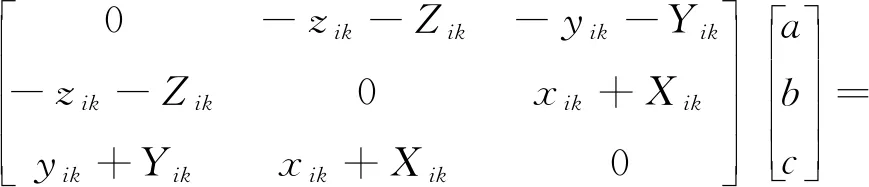
(7)

然后結合式(6)和(7)，得到

。

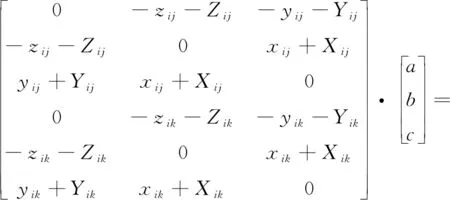
(8)

由式(8)可以計算出a、b、c三個參數，再根據式(2)和(3)可求出旋轉矩陣R，然后把R代入式(1)可以計算出平移向量T。經過上面的步驟，就可以求出平移向量T和旋轉矩陣R，這兩個參數分別包含有位置姿態傳感器在室內坐標系下的位置和姿態角。

2.3 多個公共點情況的坐標轉換算法

如果位置姿態傳感器在其視域范圍內檢測到3個以上的錨節點(n>3)，由多個錨節點估測旋轉矩陣和平移矩陣的問題就可以轉換為最小二乘問題。當兩個坐標系中存在有多個公共點，根據式(8)，列出誤差方程為

V3(n-1)×1=A3(n-1)×3·X3×1-L3(n-1)×1,

(9)

式中，X3×1=[abc]T，矩陣A3(n-1)×3和L3(n-1)×1為

L3(n-1)×1=[Xij-xijYij-yijZij-zij…
Xin-xinYin-yinZin-zin]T。

根據最小二乘原理，可得到式(9)的最優解為X=(AT·A)-1·AT·L。

根據最優解，即可求出在多個公共點情況下，羅德里格矩陣坐標轉換算法中的3個獨立參數a、b、c。由這3個參數和式(2)、(3)即可求出多個公共點情況下的旋轉矩陣R。

考慮到公共點在空間坐標系的測量誤差，根據式(1)列出其誤差方程，即

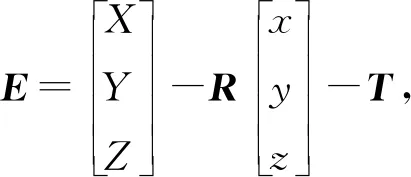
(10)

令ae=[XYZ]T，be=[xyz]T,則式(10)可以簡化為E=ae-R·be-T。

由最小二乘的矩陣推導，在滿足

min(‖ae-R·be-T‖2)2

(11)

條件下，可使誤差矩陣E達到最小，其中‖‖2表示二階范數。將式(11)展開，可得

min(‖ae-R·be-T‖2)2=

min((ae-R·be-T)T·(ae-R·be-T)),

(12)

將式(12)對平移向量T求偏導，并令其偏導值等于零，求出誤差矩陣達到最小時，平移向量的最優解為

(13)

根據式(13)，計算出3個以上的公共點分別在兩個坐標系的重心坐標，然后使用多個公共點情況下求出的旋轉矩陣R，即可求出多個公共點情況下的平移向量T。

3 仿真結果與分析

圖5是室內位置姿態測量系統的仿真模型，尺寸為5 000 mm×5 000 mm×3 000 mm，25個紅外LED作為錨節點固定在天花板上，錨節點在室內坐標系下的坐標值如表2所示。

表2 室內錨節點坐標值Tab.2 The coordinate of indoor anchorsmm

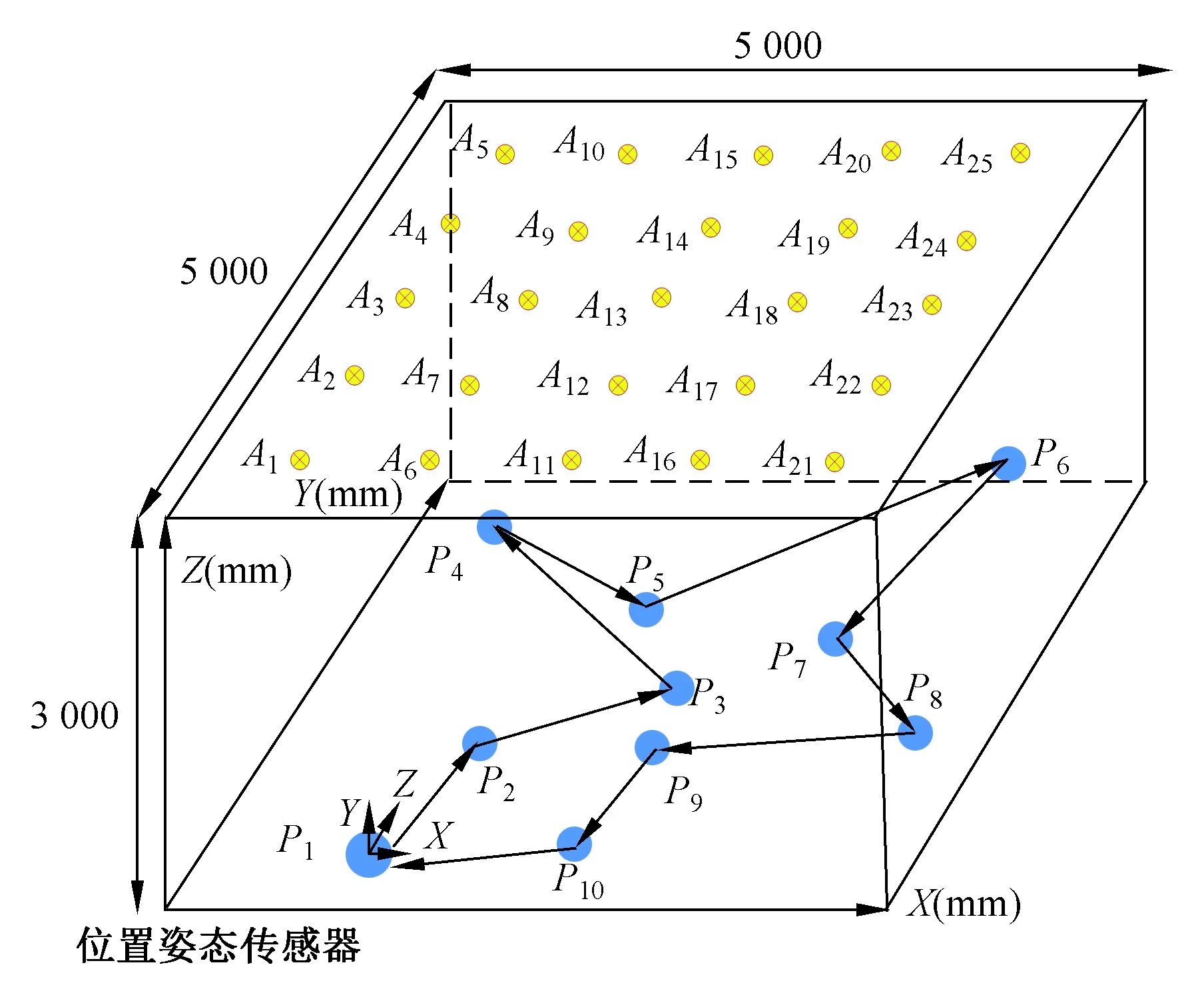
圖5 室內導航系統模型Fig.5 System model for indoor navigation

位置姿態傳感器在室內移動，從測量點P1，經過P2、P3、P4、P5、P6、P7、P8、P9、P10，最后回到P1，如圖5所示。

設定傳感器在室內坐標系下P1的位置[1 000 mm, 1 000 mm,300 mm]，俯仰角α=0°，滾轉角β= 0°，偏航角γ= 0°，因此平移向量T=[1 000 mm,1 000 mm,300 mm]。根據各個錨節點在傳感器上3個線陣CCD的投影點位置，計算后可知A1，A2，A6，A7這4個錨節點在傳感器的視域范圍內，求出錨節點A1在線陣CCD1，CCD2和CCD3上的投影點在傳感器坐標系下的坐標值分別為m1，m2，m3；A2，A6和A7在線陣CCD1，CCD2和CCD3上的投影點在傳感器坐標系下的坐標值分別為n1，n2，n3；p1，p2，p3；q1，q2，q3，如表3所示。

表3 傳感器坐標系下的相交點坐標Tab.3 The intersection in sensor coordinate system mm

根據表1中位置姿態傳感器的仿真參數，將錨節點A1，A2，A6，A7在傳感器坐標系下的交點坐標m1，m2，m3，n1，n2，n3，p1，p2，p3和q1，q2，q3與仿真參數表1相對比，這些交點坐標全部都位于CCD1,CCD2和CCD3在傳感器坐標系下的可測量范圍內。

根據表3中錨節點A1在3個線陣CCD上的坐標值m1，m2，m3，求出A1在傳感器坐標系下的坐標值為a1=[-499.99 mm,-499.99 mm,2 699.99 mm]。同理根據n1，n2，n3，p1，p2，p3，q1，q2，q3可以求出錨節點A2，A6，A7在傳感器坐標系下的坐標值為a2=[-499.99 mm,499.99 mm,2 699.99 mm]和a6=[499.99 mm,-499.99 mm,2 699.99 mm]，a7=[499.99 mm,499.99 mm,2699.99 mm]，如表4所示。

根據4個錨節點A1，A2，A6，A7在表2中室內坐標系下的坐標值和表4中傳感器坐標系下的坐標值，使用第2節的羅德里格矩陣坐標轉換算法同時求解在位置P1時傳感器的位置和姿態。

表4 傳感器坐標系下A1，A2，A6，A7坐標值Tab.4 The coordinate of A1,A2,A6,A7 in sensor coordinate system mm

同理，由P2，P3，P4，P5，P6，P7，P8，P9，P10在室內設定的位置和姿態的，按照傳感器在位置P1的計算過程和方法，可分別計算出其他9種情況下可以估測到的錨節點，如表5所示。

表5 不同位置可估測的錨節點Tab.5 Measurable anchors at different location

由表5中P2，P3，P4，P5，P6，P7，P8，P9，P10這9個位置可測量到的錨節點，按照位置P1時候的求解方法，分別求出不同位置時可估測到的錨節點在傳感器坐標系下的坐標，使用第2節的羅德里格矩陣坐標轉換算法，將不同位置時估測出的位置和姿態列于表6中。

將表6中10次計算結果在x，y，z軸3個方向的測量誤差值進行最大誤差和平均誤差統計，并根據平均誤差求出標準差，如表7所示。

同時對表6中10次計算結果在俯仰角α，滾轉角β，偏航角γ的測量誤差值進行最大誤差和平均誤差統計，并根據平均誤差求出標準差，如表8所示。

表6 傳感器在各測量點的位置和姿態Tab.6 The position and attitude of the sensor at different measurement point

由表7和表8的測量誤差評估結果，將本文提出的方法與文獻[9]的方法相對比。本文的測量誤差小于文獻[9]的方法，如表9所示，表明本文提出的位置姿態傳感器在室內導航中的可行性和高精確性。

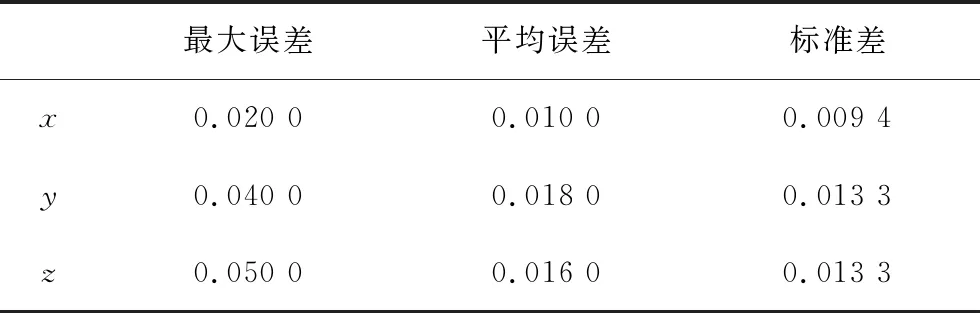
表7 位置測量誤差Tab.7 Position measurement error mm

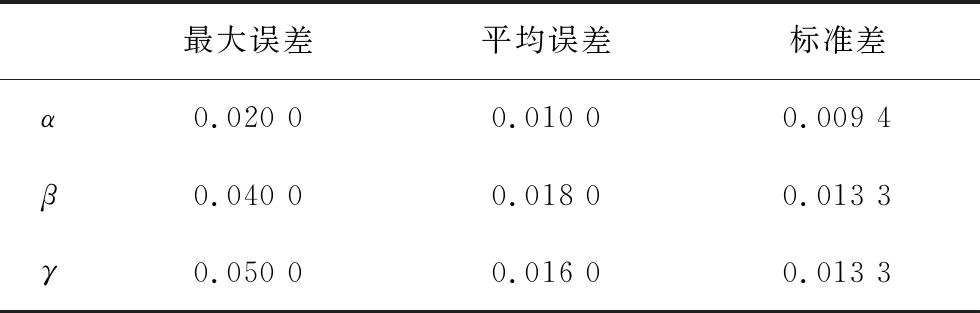
表8 姿態測量誤差Tab.8 Attitude measurement error (°)

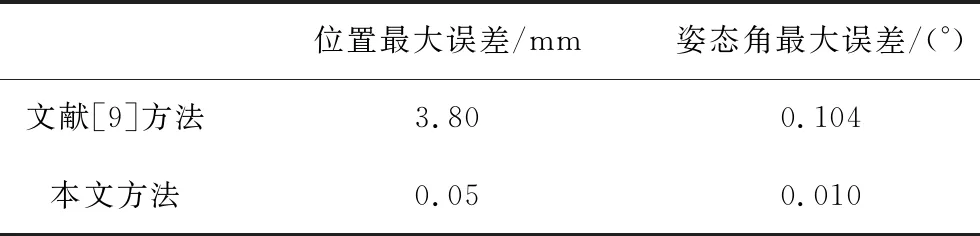
表9 兩種測量方法的誤差比較Tab.9 Error comparison between two measurement methods

4 結論和展望

本文使用3個線陣CCD和3個柱面透鏡設計了一種新型的室內位置姿態傳感器，在估測出至少3個錨節點在傳感器坐標系下的坐標之后，使用羅德里格矩陣坐標轉換算法同時估測出該傳感器在室內的位置和姿態。位置姿態傳感器不需要考慮平行或傾斜的工作情況，并且與傳統的使用3個錨點僅能估測位置的室內導航方法相比，本文提出的方法不僅可以估測傳感器在室內的位置，還可以同時估測傳感器在二維情況下的航向或三維情況下的姿態。并且在室內導航過程中，傳感器的使用個數不受限制。本文提出的方法部署成本低，易于室內大范圍擴展使用，仿真結果表明了該方法的可行性和高精度特性。

搭建實物平臺是接下來的工作，同時為了提高位置和姿態測量的實時性，位置姿態傳感器高速同步曝光多個LED錨節點也是接下來的工作重點。