輸電線強風抖振順風向動張力的理論與試驗

汪偉，汪大海，章東鴻，何運祥，向越

(1. 中國能源建設集團廣東省電力設計研究院有限公司，廣州510663；2. 武漢理工大學土木工程與建筑學院，武漢430070； 3. 中國能源建設集團西南電力設計院有限公司，成都610021)

0 引言

在大氣邊界層湍流的作用下，輸電線的動力響應復雜，導線傳遞到支撐桿塔上的風荷載變化巨大，導致桿塔的受力特性發(fā)生較大變化。現(xiàn)場實測、理論分析和風洞試驗等已有研究均表明，輸電線路體系中導線和地線傳遞給桿塔的荷載為桿塔結(jié)構(gòu)的控制荷載[1 - 3]。由于輸電線結(jié)構(gòu)振動的復雜性及風場的隨機性，目前對其形成機制的認識尚未明確，尤其是缺乏完備的動張力理論計算模型及合理的荷載評估方法，致使桿塔倒塌事件時有發(fā)生[4 - 5]。因此開展標準氣動彈性模型風洞試驗測試，并結(jié)合現(xiàn)有的頻域理論計算方法，對輸電線風振動力響應及其模態(tài)參數(shù)作深入研究是十分必要的。

風荷載作用下導線平面的非線性靜力變形和平均風偏非常顯著，使得導線張力相對初始狀態(tài)(只受重力)發(fā)生了相當大的變化，進而導致了系統(tǒng)動力特性的變化[6]。馬人樂和胡宇濱等對江陰500 kV輸電塔進行了實地模態(tài)參數(shù)識別，發(fā)現(xiàn)輸電線振動方向的不同對桿塔動力特性的影響較為明顯[7]。Okamura等通過對原型塔線體系現(xiàn)場實測，發(fā)現(xiàn)輸電塔的動力特征變化極大地影響著輸電線的動力響應，且總阻尼(結(jié)構(gòu)阻尼與氣動阻尼之和)的主要部分為氣動阻尼[8]。由于現(xiàn)場實測代價太大，在結(jié)構(gòu)風工程中沒有得到廣泛應用。但現(xiàn)場實測為縮尺風洞試驗和理論分析研究奠定了夯實的基礎(chǔ)。早年受困于風洞試驗的尺寸限制，Souza和Davenport等提出了一種只考慮第一階振型的跨度縮減氣彈模型的試驗方法[9]。在此技術(shù)上，樓文娟和孫炳楠等率先對輸電塔開展了風洞試驗研究，考察了有無導線對風振響應和風振系數(shù)造成的影響[10]。趙桂峰和謝強等完成了塔線體系的氣彈模型風洞試驗，還原了原型塔體的風致破壞形態(tài)[11]。李正良和肖正直等完成了單一塔體以及掛線塔體的氣彈模型試驗，探究了塔線體系耦合作用對風振總響應的影響[12]。以上試驗均采用跨度縮減氣彈模型的方法，參數(shù)上采用了諸多近似，并非嚴格意義上按照基本縮尺比設計的標準氣彈風洞試驗[13]。

在風致響應理論研究方面，導線的風振響應分為平均風荷載作用下的靜力響應和平均風偏狀態(tài)處脈動風引起的動力響應，其中脈動風引起的動力響應是抗風設計的重難點問題。Irvine建立了懸索的靜力平衡方程，得到了懸索結(jié)構(gòu)的懸鏈線和拋物線解析計算理論模型，并通過動力微分方程系統(tǒng)的闡述了懸索的動力特性及響應的計算方法[14]。在此理論基礎(chǔ)上，Wang等基于懸索連續(xù)體平面內(nèi)和平面外動力方程，將風荷載對輸電線的作用分解成平均風的非線性的靜力作用和在平均風偏位置處的脈動風的近似線性動力作用，從而推導了導線風振三維動張力的時域和頻域理論計算模型，并通過有限元分析發(fā)現(xiàn)平均風偏的非線性靜力狀態(tài)及氣動阻尼效應對導線順風向動張力的影響尤其顯著，理論結(jié)果證實了由于氣動阻尼較大，背景響應占順風向動力總響的主要部分[15 - 16]。

隨著現(xiàn)有試驗條件的快速發(fā)展，標準氣彈風洞試驗已成為可能。本文嚴格控制基本縮尺比參數(shù)，設計并完成了雙跨四分裂輸電線標準氣動彈性模型風洞試驗，通過高頻測力天平考察了輸電線順風向動張力的作用規(guī)律。并以耐張絕緣子邊界條件為例，將風洞試驗結(jié)果與理論計算方法進行了比較驗證。本研究為揭示輸電線風振響應的變化規(guī)律，合理預測輸電塔結(jié)構(gòu)風致抖振動張力荷載，提供了風洞試驗的基本數(shù)據(jù)和分析方法。

1 標準氣彈模型風洞試驗

1.1 模型設計與試驗工況

此次試驗在西南交通大學XNJD- 3號大型大氣邊界層風洞中進行。為了使試驗結(jié)果具有代表性，本次試驗導線型號為JL/G3A-1250/125。導線模型由康銅絲和低密度的塑料套管組成，銅絲直徑為0.089 mm。銅絲外面套有線密度為1.1 g/m且直徑為1 mm的塑料軟管，同時每隔50 cm配置1段塑料軟管，通過每米1個0.5 g的鉛絲纏繞于軟管上來為導線配重，每米配置1個間隔棒。導線原型具體參數(shù)如表1所示。

表1 導線原型參數(shù)Tab.1 Parameters of conductor prototype

考慮到導線和風洞實驗室的尺寸，以及模擬紊流邊界層尺寸等要求，模型幾何相似比定為λL=1:50。 基于氣彈模型的相似準則，不考慮跨度縮減，嚴格控制導線模型的各項縮尺比參數(shù)。保證了柯西數(shù)、斯托羅哈數(shù)、密度相似和阻尼系數(shù)一致。確定模型的各項標準縮尺比參數(shù)如表2所示。

表2 導線模型相似比Tab.2 Similarity ratio of conductor model

此次試驗輸電線模型為雙跨四分裂，每跨長度為10 m，對應實際跨長500 m，邊界條件為耐張絕緣子、I形絕緣子和V形絕緣子的3種連接方式。可將絕緣子-導線體系在沿導線方向看作鉸接[17]。本文所有研究均考慮風致響應最為不利的風向角，即垂直于導線平面90 °方向。試驗風速為2.8、4.3、5.7、7.1 m/s共4種工況，對應實際風速分別為20、30、40、50 m/s。每個工況的采樣時長為90 s，測力天平傳感器采樣頻率為1 000 Hz，量程為5 N。風洞試驗測試的主要內(nèi)容為導線模型跨中連接處的張力響應以及氣彈動力特性的識別。導線模型及其測試裝置如圖1所示。

圖1 試驗模型Fig.1 Test model

1.2 風場模擬

依據(jù)輸電塔線結(jié)構(gòu)所處地理特征，此次試驗風場選為B類地貌。風場的模擬通過在試驗段上游調(diào)試尖劈和粗糙元來實現(xiàn)。風場實測平均風剖面、湍流度剖面、縱向脈動風速功率譜及其沿著線路方向的空間相關(guān)性系數(shù)如圖2所示。

圖2 風場模擬Fig.2 Wind field simulation

2 理論計算模型

2.1 平均風偏狀態(tài)下靜力分析

研究對象為雙跨兩端懸掛于等高點處，每跨跨長為L=10 m，垂跨比d0/L=1/30～1/50的均質(zhì)懸掛輸電線。初始自重狀態(tài)下：單位長度的重力荷載為mg=q0； 縱向(沿導線跨度方向)張力為H0； 豎向位移為z0(x)； 弧垂為d0=q0L2/8H0。 導線模型布置及受力構(gòu)型如圖3所示。

圖3 導線模型布置及受力構(gòu)型Fig.3 Conductor model layout and force configuration

考慮風致響應最為不利的風向，即α=90 °。 則單位長度上的導線平均風荷載為：

(1)

(2)

(3)

代入邊界條件z0(0)=0和z0(L)=0， 解得導線面內(nèi)、面外非線性靜力位移分別為：

(4)

(5)

其中平均風偏狀態(tài)下導線縱向張力H可由式(6)得到。

(6)

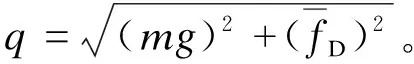
(7)

2.2 平均風偏狀態(tài)下模態(tài)參數(shù)分析

導線平面內(nèi)振動分為正對稱和反對稱振動，對于導線第i階面內(nèi)正對稱振動的頻率和振型分別為：

(8)

(9)

式中：βi為特征方程的根；bi為模態(tài)標準化的常量；同時Irvine常數(shù)λ2和導線弧長Le都由式(10)確定。

(10)

(11)

(12)

對于導線平面內(nèi)反對稱振動，其頻率和振型分別由式(13)—(14)給出。

(13)

(14)

式中a為振型標準化的常數(shù)。且有：

(15)

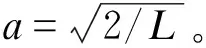
而平面外振動頻率和振型分別由式(16)—(17)給出。

(16)

(17)

1.5動力狀態(tài)下背景響應分析

結(jié)構(gòu)響應譜可以分為2部分，首先由低頻的脈動風荷載對結(jié)構(gòu)動力響應貢獻的部分，可近似為準靜力作用的響應，稱之為背景響應。而在結(jié)構(gòu)自振頻率附近的響應譜波峰體現(xiàn)了由于結(jié)構(gòu)慣性力引起的動力放大作用，稱為共振響應。

由于背景響應可近似為準靜力作用的響應，因此背景響應可以通過影響線函數(shù)進行計算。則對于任意給定的響應R(t)， 其背景響應可以表示為：

(18)

由結(jié)構(gòu)隨機振動理論，對式(18)作頻域譜分析，推導可得導線順風向動張力背景響應的功率譜密度函數(shù)為：

(19)

(20)

那么，順風向動張力背景響應的均方根σTB可以表示為：

(21)

式中corV(x1,x2)為沿導線跨度方向上x1和x2兩個位置風速的相關(guān)函數(shù)。

3 風振響應的試驗數(shù)據(jù)分析

3.1 模態(tài)參數(shù)識別

為了驗證此次輸電線風洞模型試驗完成的效果，采用Hilbert-Huang變換方法對自由振動和不同風速工況下測力天平信號進行處理，識別了導線振動的各階模態(tài)頻率和阻尼比。圖4給出了耐張絕緣子下面外自由振動(V=0 m/s)的衰減曲線及其傅里葉幅值譜圖。同理可以獲得各工況下導線振動的試驗頻率，并與2.2節(jié)理論解進行對比，對比結(jié)果如表3所示。

圖4 自由振動衰減曲線及其傅里葉幅值譜Fig.4 Free vibration decay curve and Fourier amplitude spectrum

表3 各風速下的雙跨耐張絕緣子面外振動頻率Tab.3 Out-of-plane vibration frequency of double span strain InsulatorHz

由表3可以看出，導線振動頻率均隨著風速的增大而變大，理論計算和試驗測得的二階振動頻率約為其一階振動頻率的2倍。從整體上看，不同風速下，耐張絕緣子試驗測得的導線固有頻率與理論計算結(jié)果比較吻合，表明導線模型動力特性滿足測試要求，繼而驗證了模型制作的可靠性。同時也測得了耐張絕緣子、I形絕緣子和V形絕緣子邊界條件下輸電線模型面外振動的結(jié)構(gòu)阻尼比分別為1.771%、1.730%和1.762%，與實際工程的結(jié)構(gòu)阻尼比相符合。

表4為一階面外試驗氣動阻尼比。從表中數(shù)據(jù)可以看出，試驗測量的氣動阻尼比均隨風速的增大而增大。大風工況下的氣動阻尼比遠大于結(jié)構(gòu)阻尼比，可見氣動阻尼對輸電線強風抖振動張力響應影響占主導地位。本次試驗測量的氣動阻尼與文獻[18]中試驗的結(jié)果接近。

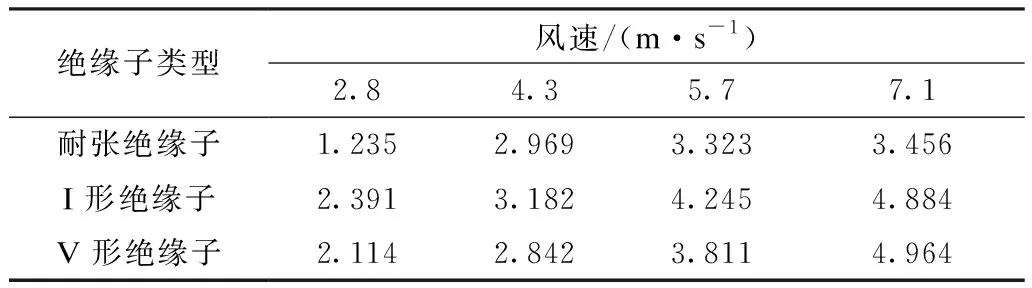
表4 一階面外試驗氣動阻尼比ξTab.4 Aerodynamic damping ratio for first order out-of-plane tests %

3.2 風偏角和阻力系數(shù)

圖5 導線風偏角度Fig.5 Windage yaw angle of conductor

圖6 阻力系數(shù)Fig.6 Drag coefficient of conductor

以上數(shù)據(jù)分析表明，導線平面風偏角度隨風速的增大而明顯增大，大致呈線性關(guān)系，不同工況下對應導線平面風偏角度最大相差僅2 °，可見絕緣子類型對導線平面的風偏角度影響不大。而導線阻力系數(shù)隨風速變化不大，整體趨勢略有增加。本文試驗測得的阻力系數(shù)與文獻[19]比較接近。3種邊界條件下，V形絕緣子條件測得的阻力系數(shù)CD最大，而耐張絕緣子與I形絕緣子條件下測得的阻力系數(shù)CD比較接近。

3.3 氣彈試驗數(shù)據(jù)分析

雙跨四分裂I形、V形和耐張絕緣子條件下，對測力天平時程數(shù)據(jù)處理后，試驗測得各級風速作用下，順風向動張力功率譜如圖7所示，順風向張力的均值、極值和均方根響應如圖8所示。

圖7 順風向動張力總響應的功率譜Fig.7 Power spectrum of total response of along-wind dynamic tension

圖8 順風向張力響應的統(tǒng)計分析Fig.8 Statistical analysis of along-wind dynamic tension

功率譜分析表明，順風向動張力響應有顯著的背景響應和共振響應，其中以共振響應面外前兩階較為明顯。由功率譜圖共振波峰可看出，一階共振響應明顯遠大于二階共振響應，可見共振響應以一階面外模態(tài)為主。對于順風向張力響應而言，從上述分析中可以發(fā)現(xiàn)，各級風速下不同邊界條件對應的動張力總響應的均值、極值和均方根都比較接近。

3.4 順風向動張力的理論試驗對比

首先對采集的時程信號數(shù)據(jù)進行去噪，將8 Hz以上的高頻信號數(shù)據(jù)濾波，然后對濾波后的動張力時程數(shù)據(jù)采用Pwelch方法進行功率譜估計，從而得到了順風向動張力的試驗總響應功率譜。繼而基于背景分量和共振分量的功率譜密度函數(shù)關(guān)系，對總響應功率譜曲線的各顯著極小值點采用3次埃爾米特(Hermit)插值多項式擬合，將功率譜的背景分量和共振分量進行了分離，從而獲得試驗測得的背景響應功率譜。由2.3節(jié)的背景響應頻域理論框架可以計算出各風速下耐張絕緣子脈動風荷載作用下順風向動張力的的背景響應功率譜與均方根。將其與試驗測得結(jié)果進行對比，功率譜比較結(jié)果如圖9所示，均方根比較結(jié)果如表5所示。

由以上圖表可以看出，順風向動張力的背景響應理論功率譜與試驗功率譜趨勢一致，理論計算的背景響應均方根占試驗總響應的88%～94%之間，試驗背景響應均方根占比在81%～97%之間，可見

圖9 順風向動張力響應的功率譜Fig.9 Power spectrum of along-wind dynamic tension response

表5 順風向動張力響應的均方根σTBTab.5 Root mean square of along-wind dynamic tension response ×10-2N

背景響應占動張力總響應的絕大部分。隨著風速的增大，試驗測得與理論計算的順風向張力的背景響應都明顯增大。整體上試驗測得和理論計算的順風向動張力背景響應的均方根非常接近。

4 結(jié)論

本文設計并完成了雙跨四分裂輸電線標準氣動彈性模型風洞試驗，考察了輸電線順風向動張力的作用規(guī)律。主要結(jié)論如下。

1) 模態(tài)參數(shù)分析表明，理論計算和試驗識別的導線振動頻率、氣動阻尼均隨著風速的大而明顯變大，不同風速下耐張絕緣子試驗測得的導線振動頻率與理論計算結(jié)果較吻合，導線氣動阻尼比遠大于結(jié)構(gòu)阻尼比。

2) 風偏角和阻力系數(shù)分析表明，導線平面風偏角度隨風速的增大而明顯增大，大致呈線性關(guān)系，絕緣子類型對導線平面的風偏角度影響不大。而導線阻力系數(shù)隨風速變化不大，但整體趨勢略有增加。3種連接方式中，V形絕緣子條件下測得的阻力系數(shù)最大，而耐張絕緣子和I形絕緣子條件下測得的阻力系數(shù)比較接近。

3) 3種連接方式下的試驗結(jié)果表明，順風向動張力響應有顯著的背景響應和共振響應，其中共振響應以一階面外振型為主。不同連接方式對應的功率譜、均值、極值和均方根都比較接近。

4) 耐張絕緣子連接方式下順風向動張力背景響應的理論與試驗對比分析表明，理論功率譜與試驗功率譜曲線吻合較好，而且理論計算的背景響應均方根和試驗結(jié)果非常接近，其中背景響應占動力總響應的絕大部分。