高速動車組接觸器復合應力加速模型研究

周建升，唐 輝，劉 廣

（1.中車青島四方機車車輛股份有限公司，山東青島 266000；2.中國鐵路廣州局集團有限公司廣州動車段，廣東廣州 510000；3.西南交通大學機械工程學院，四川成都 610031）

0 引言

隨著動車組運營規模的提高，列車運行安全性要求也越來越高。接觸器作為完成電路切換、控制與保護功能的關鍵元器件[1]，廣泛應用于高速動車組的電氣系統。一旦發生故障，將直接影響高速動車組正常運行。因此，對接觸器進行可靠性分析具有重要意義。

研究接觸器可靠性的方法需要基于產品的壽命數據[2-3]。而高速動車組為了保持安全運行，接觸器等元件在失效之前就必須進行更換，避免事故的發生。因此為了得到足夠的壽命數據，需要對接觸器進行大量的壽命試驗。隨著生產技術的不斷發展，接觸器壽命不斷提高，按照動車組上接觸器的實際使用頻率，壽命試驗可能長達數年，而通過加速實驗可以大量縮短試驗時間[4]。

加速壽命試驗的統一定義最早于1967 年由美羅姆航展中心提出[5]。該試驗在進行了合理的工程及統計假設后，通過超出正常水平的應力對試驗進行加速，利用統計模型將加速環境下的可靠性信息與物理失效規律下的信息進行轉換，從而復現出在正常應力水平下的可靠性特征的數值估計[6]。即在不改變試驗樣品的失效機理的條件下，通過增大試驗應力縮短試驗周期，提高試驗效率。

加速壽命試驗屬于統計試驗范疇，試驗中對產品所加的應力可以是溫度、電流、電流、功率、濕度、機械應力等[7]。目前加速模型多為單應力模型，未考慮應力交互項。針對以溫度為加速應力的單應力加速試驗，阿倫尼斯（Arrhenius）在1880 年提出了阿倫尼斯模型，該模型指出產品壽命隨溫度上升而呈指數下降[8-9]。針對電應力的加速試驗，其加速模型被物理上的數據證實符合逆冪率模型。同濟大學的康勁松等在分析驅動電機系統中直流母線電容單一加速模型及加速系數的基礎上，推導出了直流母線電容在溫度—電應力同時作用下的加速模型和加速系數，并通過仿真分析進行了驗證[10]。查國清等通過對智能電表的失效機理分析，設計并實施了加速試驗方案，通過對試驗數據的退化軌跡進行建模以及多應力加速模型的研究，對智能電表可靠性和壽命水平進行了綜合分析[11]。

本文所依據試驗施加溫度和電流這兩種接觸器上最常見的應力。在加速試驗的基礎上，計算出了一種復合應力加速模型，并通過實驗數據驗證復合應力加速模型的準確性。

1 單應力加速模型

1.1 阿倫尼斯模型

由于接觸器開合過程中，觸頭間會產生電弧，并且設備運行過程中線圈會出現發熱現象，二者都會引起接觸器工作環境的溫度發生變化。溫度改變將導致材料的性能發生變化，加速產品失效。阿倫尼斯模型是阿倫尼斯基于溫度為加速應力提出的模型。

其中，L 為產品的壽命特征，如中位壽命、平均壽命等；A 為大于0 的常數；E 為與材料有關的激活能，單位為eV；K為玻爾茲曼常數，8.617×10-5eV/K；T 為絕對溫度，單位為K（開爾文）。E/K 又稱激活溫度，單位為K。

激活能是一種反映溫度對產品壽命影響的指標，在低于500 K 的情況下，對確定的反應，其激活能為常數[10]。這確保了加速壽命試驗的可行性，而對于一般電子產品來說，溫度應力一般不會超過500 K。

阿倫尼斯模型表明：產品的壽命特征隨溫度上升呈指數下降。故對模型兩邊同時取對數可得：

其中，a1=lnA1，b1=E/K，a1和b1均為待定參數。從阿倫尼斯模型可知，壽命特征的對數與溫度的倒數呈線性關系。

1.2 逆冪律模型

在加速壽命試驗中，電應力作為一種常見應力也可普遍作為加速應力。在接觸器實際使用過程中，增大接觸器觸頭間的電流，會影響接觸器觸頭間的電弧。由于每次接觸器開斷觸頭間均會產生電弧對觸頭造成侵蝕，因此將電應力作為加速應力進行試驗。

在物理上很多試驗數據證明，電應力作為加速應力時，產品的壽命特征復合逆冪率模型[10]：

其中，L 為產品的壽命特征（如中位壽命、平均壽命等），A2為大于0 的常數，m 為與材料激活能有關的正常數，I 為電應力。

逆冪率模型表示產品的某壽命特征是電應力I 的負次冪函數。將模型兩邊取對數可得：

其中，c1=lnF2，d1=-m，c1和d1均為待定常數；I 大于0。

2 復合應力加速模型

產品在使用過程通常受到復雜的環境應力，對接觸器而言會受到溫度、電應力、濕度的影響。這些應力的綜合效果對接觸器的使用壽命產生了影響。但同時考慮多種應力對接觸器的壽命影響將使模型過于復雜且不利于實際應用。對于接觸器而言，電應力和溫度對接觸器壽命影響最大，因此本文加速模型只考慮溫度及電應力的影響。

2.1 無交互項的復合模型

由于接觸器本身的結構及工作原理較為簡單，因此在忽略掉溫度和電應力之間的影響的情況下。直接將溫度與電應力的影響相乘便可得到一種簡單的加速試驗模型[10]。

經分析可知，溫度加速模型服從阿倫尼斯模型，電應力加速模型服從逆冪率模型，將兩種模型相乘可得：

對該模型兩邊同時取對數可得：

其中，a3=lnA3，b1=E/K，d1=-m，a3、b1和c1均為待定常數。

2.2 考慮交互項的復合模型

Eyring 等針對溫度及電壓作為加速應力的情況，于1941 年提出了廣義艾林模型[7]。廣義艾林模型為：

其中，A′、B′、C′和D′均為待定常數，K 是玻爾茲曼常數。若令L′=LT，再對上式兩端同時取對數，可得：

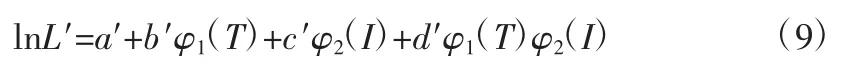
其中，a′=lnA′，b′=B′/K，c′=C′，d′=D′/K，φ1（T）=1/T，φ2（I）=I。上式中的第四項為溫度應力與電應力的交互項，為簡化模型實際使用中常忽視掉該項，但為了提高模型精度，需要對其交互項進行研究。

3 加速試驗及模型參數計算

由于高速列車所用接觸器額定電氣壽命高達50 萬次，且接觸器所處工況常優于額定工況，故而接觸器實際使用壽命次數將高于50 萬次。常規壽命試驗將耗費大量時間來對接觸器進行壽命測試，為縮短試驗周期且保證測試準確性，本文設計接觸器在溫度和電應力條件下的復合應力加速試驗。

3.1 試驗方法

根據阿倫尼斯模型，當單獨取溫度作為加速應力時，T0，T1，T2，T3，T4應按照溫度梯度的倒數呈等間隔的原則進行溫度選取，選取規則如式（10）所示：

其中，k=0，1，2，3；T0為常溫條件，25 ℃；T4為極限工作最高溫度，80 ℃。

根據逆冪率模型，在單獨取電流作為加速應力時，應按照電應力參數的對數呈等間隔的原則進行選取：

其中，k=0，1，2，3。I0=35 A，為實際使用電流，I4=100 A，為額定負載電流值。根據式（8）計算出I1、I2、I3，將對應的Tk和Ik組合形成4 個梯度的復合應力加速條件。接觸器額定參數見表1，加速實驗條件見表2。

表1 接觸器額定參數

表2 加速實驗條件

3.2 特征壽命計算

根據接觸器樣本數據，進行接觸器的威布爾分布計算和特征壽命計算。隨著應力增大，接觸器壽命逐漸縮短，需要針對不同測試應力調整測試間隔。因此條件1～條件3 測試間隔為接觸器開斷每1000 次，條件4 測試間隔為接觸器開斷每500 次，條件5 測試間隔為接觸器開斷每100 次。

以樣品1 為例進行計算，實驗共用5 個樣品，即測試總量n=5，試驗采用定數截尾法，在總樣本數量的60%失效時停止試驗，即3 個樣品失效時。試驗結束時不同條件下接觸器開斷次數情況如表3 所示。

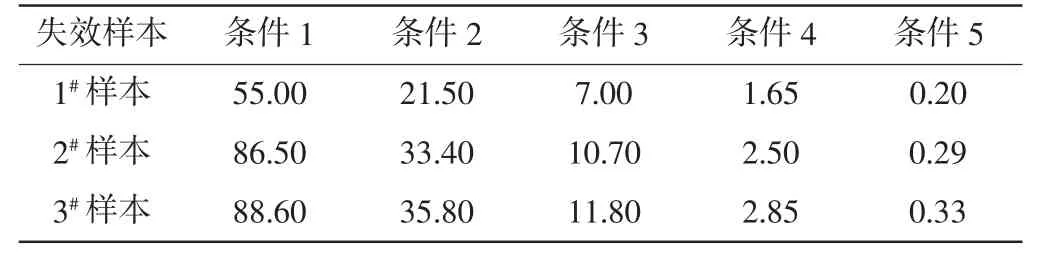
表3 接觸器失效次數 萬次

根據威布爾分布的定義，其累積分布函數為：

其中，c 為部件工作次數，β 為威布爾分布形狀參數，η 為威布爾分布尺度參數。

對式（12）進行變換可得：

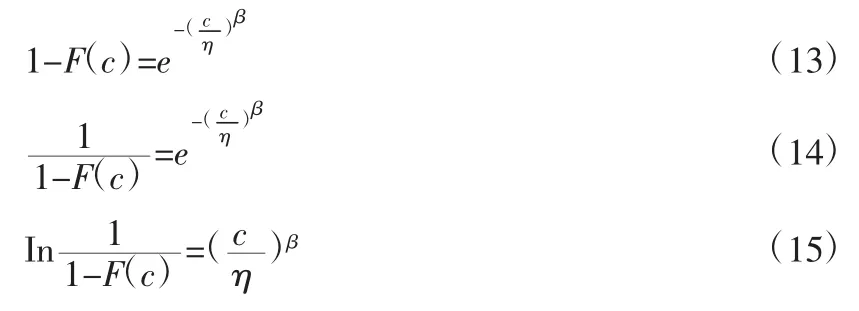
將Inc 看作自變量，y 看作因變量，β 即為擬合直線的斜率，直線與縱軸截距q=-β×Inη，則。由失效數據的中位秩確定。

其中，i 為累積失效數量，n 為測試總數量。

將樣品1 失效數據帶入上式后得到F（c），將測試數據進行變換以后，按照x=Inc 為橫坐標，y 為縱坐標，在威布爾坐標圖中進行描點（表4）。

表4 威布爾分布待擬合數據

表4 中數據通過最小二乘法擬合擬合后圖像如圖1 所示。

圖1 威布爾坐標圖

根據坐標中數據的擬合結果，得出形狀參數和尺寸參數。

由圖1 可知，擬合后直線為y=2.852 1x-39.686 6，擬合直線斜率β=2.852 1，直線與縱坐標軸截距q=-39.686 6，則尺度參數為η=1.104 4×106。由此得到第一個接觸器樣品的威布爾形狀參數β 和尺度參數η。

同理得到其余4 組接觸器樣品的威布爾形狀參數β 和尺度參數η（表5）。

表5 接觸器威布爾分布特征參數

3.3 復合模型參數計算

按照忽略應力之間的相互影響，直接相乘的模型進行擬合。

式（7）中，由b1=E/K，激活能E 選取為0.534 eV，計算可得b1=6197.05 K。將加速實驗所得特征壽命數據帶入式（7），可解得不考慮溫度與電應力之間影響的模型為：

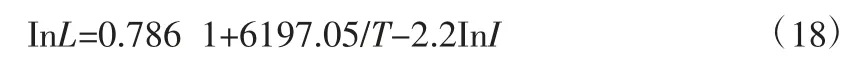
將式兩邊同時取自然常數為底數的指數運算得：

將加速實驗特征壽命數據帶入式（9）中解得參數為：

帶入式（9）可得復合應力加速模型為：

4 應力模型準確性對比分析

將常規實驗的條件參數T=298.15 K、I=35 A 代入無交互項的加速應力模型即式（19）中，可得預測結果L1=936 108。

將常規實驗的條件參數T=298.15 K、I=35 A 代入考慮交互項的加速應力模型即式（21）中，可得預測結果L2=1 023 369。

根據加速實驗數據分析可知，常規實驗的特征壽命為L0為110.44 萬次。

預測準確率為：

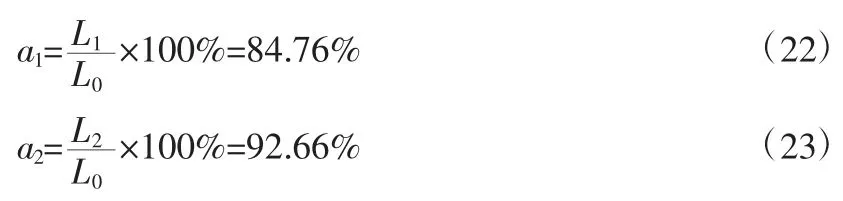
其中，a1、a2分別為不考慮溫度與電應力交互項與考慮交互項模型的預測準確率。通過常規實驗特征壽命驗證，含交互項的復合應力加速模型相較于不含交互項的復合加速模型壽命預測準確率提升了7.9%。

5 結束語

本文通過接觸器的加速試驗對接觸器的可靠性進行研究，結合接觸器額定運行工況以及加速實驗的研究，設計并完成溫度和電應力的復合應力加速試驗。通過對接觸器加速實驗下失效樣本壽命進行分析，計算出為威布爾分布模型及各個加速條件下的樣本特征壽命。

通過樣本特征壽命分別推導出不含交互項和考慮交互項的復合應力加速模型，并對模型參數進行求解。利用兩種加速模型分別映射到常規實驗條件計算特征壽命。通過對比分析，證明相較于忽略應力交互項的模型，考慮溫度和電應力之間影響的復合應力模型對接觸器壽命預測準確率提升了7.9%，對接觸器的壽命預測方法及加速應力模型具有指導作用。

基金項目：中國鐵路總公司科技研究開發計劃項目（編號：P2018J001）。