基于有限元方法的平房倉(cāng)中小麥堆的密度分布研究

陳 雪 程緒鐸 胡美珠

(南京財(cái)經(jīng)大學(xué)食品科學(xué)與工程學(xué)院；江蘇省現(xiàn)代糧食流通與安全協(xié)同創(chuàng)新中心，南京 210046)

當(dāng)小麥儲(chǔ)藏在平房倉(cāng)中時(shí)，糧堆受到自身質(zhì)量、內(nèi)摩擦力以及倉(cāng)壁與糧堆之間的摩擦力作用，產(chǎn)生壓應(yīng)力和切應(yīng)力[1]。小麥的籽粒松軟，糧堆各處的應(yīng)力作用導(dǎo)致糧堆產(chǎn)生形變和體積壓縮，體積壓縮導(dǎo)致糧堆密度的增加，平房倉(cāng)內(nèi)小麥堆的應(yīng)力分布是不均勻的，所以小麥堆密度分布也是不均勻的。每年我國(guó)均需投入大量人力、物力和資金開(kāi)展清倉(cāng)查庫(kù)工作[2]。糧食儲(chǔ)藏?cái)?shù)量檢查是糧食庫(kù)存檢查的一項(xiàng)重要內(nèi)容[3]，即通過(guò)一定的手段獲取糧倉(cāng)中所儲(chǔ)存糧食的數(shù)量，主要包括稱(chēng)重法和體積密度法[4]。稱(chēng)重法工作量大、效率低，在大規(guī)模的庫(kù)存檢查中很難廣泛使用。體積密度法是指通過(guò)測(cè)量糧堆的體積和平均密度計(jì)算糧倉(cāng)中糧食數(shù)量的檢查方法。現(xiàn)有的體積密度法是使用糧食的表層密度乘以修正系數(shù)來(lái)獲取糧堆的平均密度，修正系數(shù)是憑經(jīng)驗(yàn)給出的，此方法誤差較大。因此，只有準(zhǔn)確計(jì)算或測(cè)量出平房倉(cāng)中的密度分布值才能準(zhǔn)確快捷地計(jì)算平房倉(cāng)中小麥堆的總質(zhì)量。

前人通過(guò)在糧倉(cāng)底部安裝了壓力傳感器[5,6]，測(cè)定糧倉(cāng)底部的壓力分布，從而估算出糧堆的總質(zhì)量，此方法成本高且只能得出糧堆總質(zhì)量而無(wú)法得出糧倉(cāng)內(nèi)糧堆密度分布值。程緒鐸等[7]開(kāi)發(fā)了一個(gè)分層壓縮模型來(lái)預(yù)測(cè)平房倉(cāng)中的糧堆密度和壓力分布，但其假設(shè)平房倉(cāng)中同一糧層的密度是相同的，而實(shí)際中平房倉(cāng)內(nèi)同一糧層的堆密度分布是不均勻的，該分層壓縮模型不能準(zhǔn)確給出平房倉(cāng)中的糧堆的密度分布值。

自20世紀(jì)70年代開(kāi)始，有限元法被用來(lái)研究糧倉(cāng)中物料的應(yīng)力分布及倉(cāng)壁的壓力問(wèn)題。Jofriet[8]采用線彈性模型，用有限元方法研究了直筒倉(cāng)內(nèi)物料靜態(tài)時(shí)的應(yīng)力分布問(wèn)題。Ooi[9]使用有限元方法研究了柔性筒倉(cāng)內(nèi)散體的應(yīng)力分布。國(guó)際上一些研究人員構(gòu)建了許多本構(gòu)方程，例如：Mohr-Coulomb模型、Drucker-Prager模型和Lade-Duncan模型等，通過(guò)有限元方法研究了糧倉(cāng)中物料的應(yīng)力分布問(wèn)題。這些研究很好地計(jì)算出了儲(chǔ)藏在筒倉(cāng)中壓縮性很小的沙子、碎石、工業(yè)物料的應(yīng)力分布，這些彈塑性本構(gòu)方程也可以較準(zhǔn)確地求解出糧倉(cāng)內(nèi)糧堆的應(yīng)力分布。糧食與土壤、沙子等物料的力學(xué)特性有很大的差異，小麥籽粒松軟，籽粒間的孔隙大，小麥堆在受壓時(shí)體積變化大且體積變化同時(shí)發(fā)生在彈性變形和塑性變形兩個(gè)階段。但研究所使用的本構(gòu)方程均假定物料的體積變化很小且只發(fā)生在彈性變形階段，形狀變化發(fā)生在塑性變形階段。因此這些模型難以反映小麥堆變形時(shí)的應(yīng)力與應(yīng)變關(guān)系，用它們求解平房倉(cāng)內(nèi)小麥堆的應(yīng)變分布是不準(zhǔn)確的。1968年，Roscoe[10]提出了修正劍橋模型(Modified Cam Cay)，修正劍橋模型既考慮了彈性階段的體積與形狀變化又考慮了塑性階段體積與形狀的變化，修正劍橋模型以體積應(yīng)變與剪切應(yīng)變作為應(yīng)變量，且屈服面為平均主應(yīng)力屈服面，適合松軟的散粒體的大體積變形特征，被廣泛應(yīng)用于土壤力學(xué)[11,12]。

目前鮮有將修正劍橋模型應(yīng)用于平房倉(cāng)中小麥堆密度分布的研究。本實(shí)驗(yàn)將使用有限元軟件求解修正劍橋模型計(jì)算平房倉(cāng)內(nèi)的小麥堆密度分布值。

1 材料與方法

1.1 實(shí)驗(yàn)材料

小麥，品種名為淮麥44號(hào)，產(chǎn)地江蘇南京，原始含水率為12.03%w.b., 小麥籽粒的大直徑、中直徑和小直徑分別為5.88、3.07、2.79 mm。取 10 kg小麥樣品，放置在太陽(yáng)光下晾曬 24 h，測(cè)得其含水率為 9.72% w.b.，再取 20 kg小麥樣品，分成 2 份，各自加適當(dāng)?shù)恼麴s水，然后將其裝入塑料袋中封閉好，放置恒溫箱中，溫度選定 5 ℃，1周后從恒溫箱中取出，測(cè)得2份小麥樣品含水率分別為16.55%w.b.和14.61%w.b.。用標(biāo)準(zhǔn)烘箱干燥法將 10 g 樣品在 130 ℃下干燥 19 h，重復(fù) 3 次，測(cè)定小麥的含水率。這樣，實(shí)驗(yàn)用的小麥的含水率分別為 16.55%、14.61%、12.03%和9.72% w.b.。

1.2 實(shí)驗(yàn)儀器

HG202-2(2A/2AD)電熱干燥箱，LKY-1型糧食孔隙率測(cè)定儀，SLB-6A型應(yīng)變控制式三軸儀，HGT-1000A 容重儀。

1.3 修正劍橋模型

修正劍橋模型是一個(gè)應(yīng)力-應(yīng)變關(guān)系的彈塑性本構(gòu)模型[13]。受到外界力作用時(shí)，物體產(chǎn)生的應(yīng)變?cè)隽堪w積應(yīng)變?cè)隽縟εv和剪切應(yīng)變?cè)隽縟εs，而它們分別是由彈性應(yīng)變?cè)隽亢退苄詰?yīng)變?cè)隽拷M成：

(1)

(2)

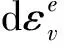
修正劍橋模型為[11]：

(3)

(4)

(5)

(6)

(7)

式中：q為廣義剪切力/kPa；p為平均主應(yīng)力/kPa；K=E/(3(1-2ν)),K為體積模量/kPa ；G=E/(2(1+ν)),G為剪切模量/kPa。

由式(4)～式(7)可知，修正劍橋模型的參數(shù)為臨界狀態(tài)應(yīng)力比M、等向膨脹指數(shù)κ、對(duì)數(shù)硬化模量λ、彈性模量E、泊松比υ、初始孔隙比e0。

1.4 小麥的修正劍橋模型參數(shù)測(cè)定

使用 HGT-1000A 容重器測(cè)定小麥堆無(wú)壓縮密度(糧倉(cāng)表層小麥密度)ρ0；使用 LKY-1 型糧食孔隙率測(cè)定儀測(cè)定小麥堆的修正劍橋模型參數(shù)初始孔隙比e0；使用 TSZ-6A 應(yīng)變控制式三軸儀測(cè)定小麥的修正劍橋模型參數(shù)E、υ、M、κ、λ。

1.5 平房倉(cāng)倉(cāng)壁的幾何與力學(xué)參數(shù)

混凝土倉(cāng)壁可視為剛性體，在有限元分析過(guò)程中不產(chǎn)生變形。平房倉(cāng)尺寸參考南京鐵心橋國(guó)家糧食儲(chǔ)備庫(kù)中糧倉(cāng)的實(shí)際大小，具體倉(cāng)壁材料的幾何與力學(xué)參數(shù)見(jiàn)表1。

表1 平房倉(cāng)及其材料的參數(shù)

1.6 平房倉(cāng)中小麥堆有限元模型構(gòu)建與運(yùn)行步驟

在Part步驟中采用三維可形變模型(3D Deformable)建模，創(chuàng)建平房倉(cāng)和小麥堆部件，尺寸見(jiàn)表1；在Property步驟中分別設(shè)定倉(cāng)壁的材料屬性和糧堆的塑彈性屬性(修正劍橋模型選擇塑性模型Clay Plasticity和彈性模型Porous Elastic)；在Assembly 步驟中將平房倉(cāng)倉(cāng)壁和糧堆部件組合起來(lái)；在 Step步驟中設(shè)定分析步； Interaction步驟是定義各個(gè)部件之間的相互接觸關(guān)系。糧堆與倉(cāng)壁之間存在相互作用，在ABAQUS中設(shè)定一個(gè)完整的接觸必須包括兩個(gè)部分：一是接觸對(duì)，選擇點(diǎn)對(duì)面離散方法，選擇倉(cāng)壁內(nèi)側(cè)面為主接觸面，糧堆外側(cè)面為從屬接觸面；二是定義相互作用力，兩個(gè)接觸面之間會(huì)產(chǎn)生摩擦力。其中，庫(kù)侖模型是較為常用的摩擦模型，即通過(guò)摩擦系數(shù)來(lái)描述兩表面間的摩擦關(guān)系。

在Load步驟進(jìn)行載荷以及邊界條件的設(shè)定，約束平房倉(cāng)倉(cāng)底和倉(cāng)壁的位移。由于平房倉(cāng)中的糧堆受到自重，通過(guò)體積力來(lái)加載。

在 Mesh 模塊中對(duì)模型進(jìn)行網(wǎng)格劃分。小麥堆模型共被劃分為9層，將每層糧堆部件均等分為1 m2的單元(圖1)。本實(shí)驗(yàn)采用節(jié)點(diǎn)法，提取各個(gè)節(jié)點(diǎn)應(yīng)力應(yīng)變值進(jìn)行計(jì)算；在Job步驟中對(duì)構(gòu)建的模型進(jìn)行運(yùn)算；待運(yùn)算成功后，在Visualization步驟中查看運(yùn)算結(jié)果提取所需數(shù)據(jù)。

建立有限元模型，平房倉(cāng)內(nèi)小麥堆長(zhǎng)26 m，寬24 m，高9 m(重力未施加，糧堆無(wú)壓縮狀態(tài))。

1.7 小麥堆節(jié)點(diǎn)密度的計(jì)算

有限元軟件計(jì)算后提取小麥堆中各個(gè)節(jié)點(diǎn)的應(yīng)變值，小麥堆節(jié)點(diǎn)密度可以由式(8)計(jì)算得到。

(8)

1.8 平房倉(cāng)中小麥堆的糧層平均堆密度

限元軟件計(jì)算后提取小麥堆中各個(gè)節(jié)點(diǎn)的應(yīng)變值，小麥堆的第i層平均堆密度可由式(9)計(jì)算。

(9)

式中：ρi為第i層小麥層的平均堆密度/kg/m3；Vijk為ijk個(gè)節(jié)點(diǎn)所在處的單元體積/m3；m是沿寬度方向的單元數(shù)，n是沿長(zhǎng)度方向的單元數(shù)。

2 結(jié)果與分析

2.1 小麥的修正劍橋模型參數(shù)及無(wú)壓縮密度

實(shí)驗(yàn)測(cè)定的修正劍橋模型的參數(shù)及無(wú)壓縮密度見(jiàn)表2。

表2 修正劍橋模型參數(shù)表及無(wú)壓縮密度

2.2 平房倉(cāng)中小麥堆的密度分布

2.2.1 同一糧層小麥堆密度分布

平房倉(cāng)中的小麥堆是一個(gè)軸對(duì)稱(chēng)的長(zhǎng)方體，選擇其中的四分之一小麥堆來(lái)分析其堆密度。由式(8)計(jì)算出平房倉(cāng)內(nèi)小麥堆的各節(jié)點(diǎn)的堆密度，本文給出了平房倉(cāng)中小麥堆(含水率為12.03% w.b.)的第2、5、8層的堆密度分布，見(jiàn)圖1(設(shè)平房倉(cāng)的拐角為原點(diǎn))。

由圖1可知，平房倉(cāng)內(nèi)在同一糧層的小麥堆的堆密度分布是不均勻的。在同一糧層中，隨著距倉(cāng)壁越遠(yuǎn)，小麥的堆密度越大，并且在該層的中間趨于穩(wěn)定值。在同一糧層中，在平房倉(cāng)的拐角附近的小麥的堆密度迅速下降，拐角處的小麥堆密度達(dá)到該層的最低值。不同糧層之間的小麥堆密度也存在明顯差異，小麥糧層深度越深，其拐角的堆密度變化越大，該糧層密度分布越不均勻。

圖1 含水率12.03%w.b.的小麥堆不同糧層的堆密度

2.2.2 小麥堆的糧層平均堆密度

根據(jù)式(9)計(jì)算得到小麥的4個(gè)不同含水率各糧層平均密度，見(jiàn)表3。

表3 不同含水率的小麥堆的不同糧層平均密度

由表3可知，在平房倉(cāng)內(nèi)，在同一含水率下，小麥堆的糧層平均密度隨深度增加而增加，但增加率隨深度增加而減小。當(dāng)含水率分別為9.72%、12.03%、14.61%、16.55% w.b.時(shí)，小麥的糧層深度分別從0增至7.62、7.65、7.73、7.81 m時(shí)，小麥的堆密度分別從802.3增至841.6 kg/m3、787.3增至829.8 kg/m3、752.5增至794.9 kg/m3和739.8增至782.7 kg/m3。

2.2.3 小麥堆的平均堆密度與含水率的關(guān)系

由表3中的數(shù)據(jù)計(jì)算出各個(gè)含水率下的平房倉(cāng)內(nèi)小麥的平均堆密度。含水率分別為9.72%、12.03%、14.61%、16.55% w.b.時(shí)，小麥的平均堆密度分別為827.8、816.1、782.1、770.5 kg/m3，其與無(wú)壓縮時(shí)的密度相比，增加率分別為4.39%、4.75%、5.12%、5.33%。平房倉(cāng)中小麥堆的平均密度隨含水率的增加而減小，平均密度相對(duì)于無(wú)壓縮密度的增加率隨含水率增加而增大。

2.3 平房倉(cāng)中小麥堆的密度與含水率和糧層深度關(guān)系模型

設(shè)關(guān)于平房倉(cāng)中小麥堆(淮麥44號(hào))糧層平均密度與糧層深度、含水率的關(guān)系方程見(jiàn)式(10)。

ρi=ρ0+(ρmax-ρ0)(1-eah3+bh2+ch+d)

(10)

式中：ρi為小麥堆第i層平均密度/kg/m3；ρ0為小麥堆表層平均密度/kg/m3；ρmax為小麥堆最深層平均密度/kg/m3；h為小麥堆糧層深度/m。

首先求出小麥的表層密度和最深糧層平均密度與于含水率的關(guān)系式。由表3中的數(shù)據(jù)，小麥堆表層密度與含水率的關(guān)系擬合為線性方程(11)。

ρ0=-9.686 6MC+898.61，R2=0.978 3

(11)

式中：MC為小麥的含水率/%w.b.。

平房倉(cāng)中小麥堆最深層平均密度與含水率的關(guān)系可擬合為線性方程見(jiàn)式(12)。

ρmax=-9.2213MC+934.22，R2=0.968 5

(12)

將式(10)兩端取對(duì)數(shù)式：

(13)

將a、b、c、d的值和式(11)、式(12)代入式(10)，得到平房倉(cāng)中小麥堆糧層平均密度ρ與含水率MC、糧層深度h的關(guān)系模型為：

ρ=-9.688 66MC+898.61+(35.61+0.465 3MC)(1-e-0.016 5h3+0.150 5h2-0.614 3h-0.01)

(14)

圖2為由式(14)預(yù)測(cè)的小麥糧層的平均密度與與含水率、糧層深度的關(guān)系曲線。方程(14)的預(yù)測(cè)值與有限元方法的計(jì)算值的相對(duì)誤差低于0.05%，RMSE的值在0.9～2 kg/m3之間，誤差較小。

圖2 糧層平均密度與含水率、糧層深度的關(guān)系

2.4 實(shí)倉(cāng)驗(yàn)證

以南京鐵心橋國(guó)家糧食儲(chǔ)備庫(kù)提供的小麥的實(shí)倉(cāng)數(shù)據(jù)作為驗(yàn)證參數(shù)[14]，所得到賬面實(shí)際小麥的總質(zhì)量與修正劍橋模型計(jì)算得到小麥的總質(zhì)量進(jìn)行對(duì)比，見(jiàn)表4。

用本修正劍橋模型計(jì)算所得的小麥總質(zhì)量與南京鐵心橋國(guó)家糧食儲(chǔ)備庫(kù)提供的實(shí)倉(cāng)中小麥總質(zhì)量比較接近，誤差在0.93～1.64%之間，誤差較小，說(shuō)明修正劍橋模型計(jì)算出的密度分布值的精度高。

表4 修正劍橋模型模型計(jì)算的小麥堆質(zhì)量與實(shí)際儲(chǔ)糧質(zhì)量的對(duì)比

3 討論

3.1 裝糧方式對(duì)糧堆密度的影響

不同的裝糧方式糧食下落的速度不同，下落的糧食對(duì)糧堆產(chǎn)生的沖擊力不同，糧食落點(diǎn)處的密度與沖擊力的大小有關(guān)。對(duì)于小型糧倉(cāng)或裝糧容器，由于糧堆高度不高，裝糧方式對(duì)裝糧后的糧堆密度有一定的影響。對(duì)于高大的平房倉(cāng)，盡管糧食沖擊力改變了糧食落點(diǎn)密度(相對(duì)于糧食下落速度為零的糧堆落點(diǎn)密度)，后續(xù)下落的糧食壓住了先前的糧食落點(diǎn)，隨著糧食的不斷下落，落點(diǎn)上方的壓力越來(lái)越大，落點(diǎn)上方的壓力改變糧食落點(diǎn)密度，這種改變?nèi)〈藳_擊力對(duì)糧食落點(diǎn)密度的改變量，即沖擊力對(duì)糧食落點(diǎn)密度的改變量有壓力引起的密度改變量代替了。對(duì)于4 m以上堆高的糧堆，除了糧堆表層，裝糧方式對(duì)糧堆各處的密度影響很小，可以略去不計(jì)。所以本研究可適用于各種裝糧方式。

3.2 平方倉(cāng)中糧堆密度分布值的驗(yàn)證

本研究計(jì)算出平房倉(cāng)內(nèi)糧堆的密度三維分布值。目前還無(wú)法直接測(cè)量出糧堆內(nèi)部各點(diǎn)的密度值，因此，無(wú)法使用實(shí)驗(yàn)來(lái)驗(yàn)證平房倉(cāng)內(nèi)糧堆各處的密度值。本研究以南京鐵心橋國(guó)家糧食儲(chǔ)備庫(kù)的平房倉(cāng)為例，將計(jì)算出的糧堆各點(diǎn)糧塊的密度乘以糧塊體積，然后求和得到糧堆總質(zhì)量。將這個(gè)總質(zhì)量與實(shí)際賬面儲(chǔ)糧質(zhì)量比較，兩者幾乎一致(誤差≤1.64%)，間接說(shuō)明本研究的計(jì)算結(jié)果是可靠的。

4 結(jié)論

以劍橋修正劍橋模型為小麥堆應(yīng)力與應(yīng)變關(guān)系本構(gòu)模型，有限元方法求解平房倉(cāng)內(nèi)小麥堆(長(zhǎng)26 m，寬24 m，高7.62～7.81 m。)的修正劍橋模型，從而計(jì)算出平房倉(cāng)中的小麥堆密度分布值。結(jié)果表明，小麥儲(chǔ)藏在平房倉(cāng)中時(shí)，其堆密度分布是不均勻的。小麥平均層密度隨著糧層深度的增加而增大；當(dāng)含水率分別為9.72%、12.03%、14.61%、16.55% w.b.時(shí)，小麥的糧層深度和堆密度增加。在同一糧層下，小麥的堆密度隨距倉(cāng)壁的距離減小而減小，在糧倉(cāng)的拐角處糧堆密度達(dá)到該層的最小值，在該層的中間位置密度到達(dá)最大值，當(dāng)糧層深度越深，該層的糧堆密度分布越不均勻。平房倉(cāng)內(nèi)小麥的平均堆密度隨著含水率的增加而減小，平均堆密度相對(duì)于無(wú)壓縮密度的增加率隨含水率增加而增大。平房倉(cāng)中小麥堆平均層密度與糧層深度、含水率之間關(guān)系方程為：ρ=-9.689MC+888.61+(35.61+0.4653MC)(1-e-0.016 5h3+0.150 5h2-0.614 3h-0.01)。

實(shí)倉(cāng)驗(yàn)證得到，由該模型計(jì)算的平房倉(cāng)中小麥的總質(zhì)量與實(shí)際糧倉(cāng)的賬面小麥總質(zhì)量誤差小，相對(duì)誤差在0.94%～1.64%之間。