基于模糊突變的水利工程脆弱性評價探討

朱遠東，歐正蜂

(1.廣東省水利水電科學研究院，廣東 廣州 510635；2.廣東省水動力學應用研究重點實驗室，廣東 廣州 510635；3.河口水利技術國家地方聯合工程實驗室，廣東 廣州 510635)

近年來，我國出現大范圍極端溫度、強降水和強臺風等極端性天氣，導致水利工程系統的不確定性日益凸顯，次生自然災害頻發，使得水利工程系統風險和脆弱性不斷增加。由于水利工程系統具有多層次多維度的特性，各子系統聯系密切，高度耦合，特別是當突發、極端事件發生時，其運行過程受內、外部因素的脅迫和擾動更為劇烈，系統的穩定性能將大幅降低。若脅迫和擾動作用突破了系統自我恢復極限，則會造成嚴重的后果，甚至引發系統崩潰。由于傳統線性模型難以實現對水利工程脆弱性的激發因素及其復雜的不確定突發過程進行解析，而Rene·Thom所創立的突變理論在處理非線性的突發性事件問題表現出色，因此被廣泛的應用于工程領域。

有關脆弱性的研究起源于20世紀80年代對致災因子論的反思[1]。1975年，White拓展了防災減災研究范疇，率先對人類面對洪災時的脆弱性進行了研究[2]。當前有關水利學科的脆弱性研究主要集中在水資源、水環境領域，而對于水利工程的脆弱性研究則涉及很少。如黃木易[3]等基于網格單元尺度對1970—2015年間巢湖流域水環境保護區景觀生態脆弱性進行分析研究；張永芳[4]、任源鑫[5]、杜娟娟[6]等通過構建多維度的脆弱性評價指標體系，采用AHP—熵權、綜合指數評估、綜合賦權等方法，分別對河北、陜西和山西省水資源的脆弱性予以評價。因此，本文基于突變理論，引入模糊數學，建立模糊突變模型并對水利工程的脆弱性進行研究分析和量化評價，可為水利工程的風險評價提供參考。

1 基本理論

1.1 突變理論

突變理論是由法國數學家雷勒·托姆(ReneThom)于1972年創立的，以突破學、奇點理論為數學工具，對基于未知系統的內部作用的研究尤為適用，可較好地解決不連續問題，為研究自然界中突變現象的數學橋梁和紐帶。突變理論中以控制變量和狀態變量來描述系統，其中系統突變原因的連續變化因素稱為控制變量，而系統的行為狀態用狀態變量表示。一般意義上的突變理論，實際指的是由Thom根據空間中分歧集的幾何形態所總結出的7種初等突變模型，即拋物形、橢圓形、雙曲形、蝴蝶形、燕尾形、尖角形和折線形。

在工程實際中，尖點、燕尾和蝴蝶型突變模型應用比較廣泛，目前已被引入到災害系統研究[7-8]，脆弱性分析評價[9-10]，工程安全評價[11-12]、風險評價[13-14]以及穩定性分析[15-17]等實際工程問題和理論研究中，取得了較好的應用效果。

1.2 模糊聚類分析法

模糊聚類分析數據數理統計中多元分析的一種，是按照特定標準來鑒別事物間的接近程度，并將性質接近的事物進行歸類的數學方法[18]。由于客觀事物之間并沒有明確的界限，為模糊數學理論的誕生及其引入聚類分析提供了理論基礎。

2 模糊突變評價指標體系構建

當突發性事件發生時，水利工程的脆弱性極其容易被激發，究其原因，主要來源于水利工程自身因素和外在因素的共同作用。因此，充分挖掘和分析水利工程脆弱性觸發的驅動因子，建立符合水利工程特性的脆弱性評價指標體系，對水利工程的風險評價分析具有重要的意義。

2.1 評價指標選取

由于水利工程在運行過程中同時受到內外界活動的干擾作用，其脆弱程度與系統承受的破壞和恢復活動具有直接相關性。當恢復活動程度可以制約破壞活動的發展時，水利工程則處于穩定狀態；反之，水利工程則向潰決的方向演化。當影響系統穩定性的破壞活動無法制約時，系統的脆弱性會被極大地激發并發生突跳，導致系統從安全狀態跳躍到崩潰狀態，由此水利工程的穩定性被破壞，將導致水災害事件發生。

綜合考慮水利工程系統的復雜性和影響因素的多層次性，本文將整個系統逐級細分成由多個指標組成的多層系統，將激發水利工程系統脆弱性的控制變量分為3個層次。原生脆弱性包括突發事件指數(E)、工程地質狀況(G)、水文氣象條件(H)以及自然地理環境概況(N)4個方面影響因素，包含4項定性指標和9項定量指標；水利工程外在脆弱性主要來源于技術(T)、管理(M)、社會(S)以及人員(P)脆弱性4個層面，包含13項定性指標。

依據突變理論原理，通過指標重要性程度排序，按照底層指標數量，選用尖點突變(J)、燕尾突變(Y)和蝴蝶突變模型(H)等不同突變模型，按照歸一公式逐層向上量化遞歸運算，求得最高層評價指標突變級數值，對照評判集進行脆弱性評價(評價指標體系見圖1)。

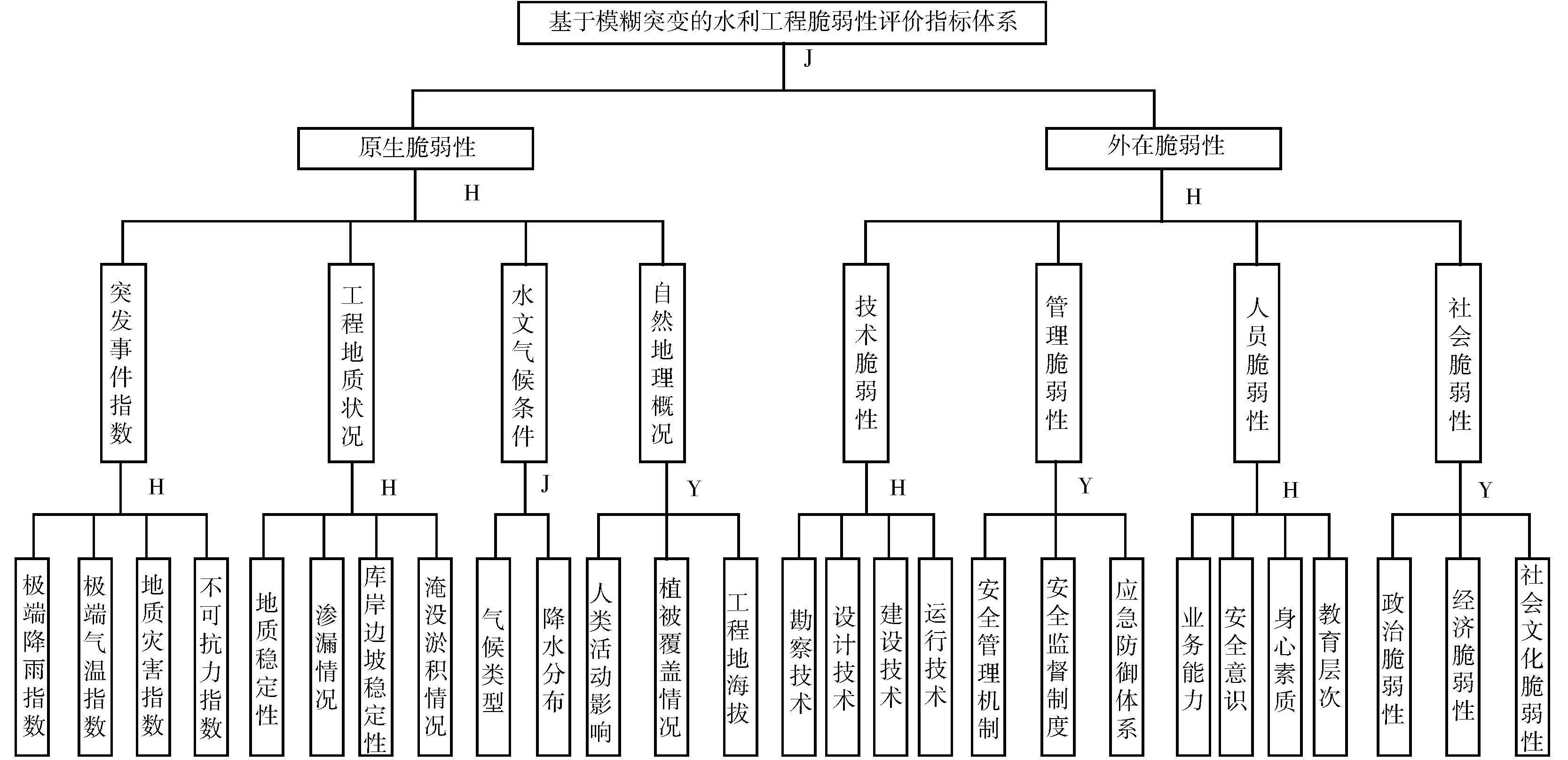
圖1 水利工程脆弱性評價指標體系示意

2.2 評價指標處理

在指標評價過程中，通常是定性和定量指標并存，因此通常采用定性與定量相結合的方法得到相關底層指標的初始值。對于模糊、不確定性的定性指標，參照文獻[19]通過采用專家打分法和模糊綜合評價相結合的方法進行規格化處理。定量指標采用極差變換法進行無量綱化處理。對于正向指標，按式(1)進行轉換，逆向指標則按式(2)進行轉換，從而將原始數據轉化為[0，1]區間上的越大越優型指標值。

(1)

(2)

為使模型中的各變量指標的性質和量綱統一，控制變量的數值分別作放大和縮小處理，則可將其取值制滿足條件的模糊隸屬函數取值區間內，由此可推出常見初等突變模型的歸一公式見表1所示。

表1 常見突變模型的歸一公式

2.3 確定隸屬函數值

水利工程脆弱性評價指標眾多，部分指標可能密切關聯，甚至可以相互替代，因此，在對水利工程脆弱性進行模糊突變綜合評價時，要充分考慮指標間的關聯性。當各控制指標間具有明顯相關性，則適用“互補”原則，即以控制變量對應的突變隸屬函數的平均值作為系統的x值；反之，適用“非互補”原則，取最小值。在計算過程中，根據底層指標數量分別選用尖點突變、燕尾突變和蝴蝶突變模型相對應的歸一公式，由指標底層逐層向上進行量化遞歸運算，最終求得最高層評價指標突變級數值，并依據評判集進行脆弱性評價。

2.4 確立評判集

根據水利工程脆弱性評價實際情況，將水利工程評價指標的評判等級劃分為4類：不脆弱、低度、中度和脆弱。各評判等級評級值區間根據底層指標賦值逐步向上層遞歸推算求得，當底層所有指標評價值為Yij=1時，則最高層綜合評價值V=1，表示水利工程不存在任何脆弱性；反之當Yij=0，表示水利工程系統已經崩潰。

參考已有研究成果[20-22]，按照可靠度和水利工程設計規范，結合水利工程實際，各底層指標分別取0.6、0.8和0.9作為水利工程高、中、低度脆弱和不脆弱的臨界值，并由底層指標逐步向上層遞歸求得最高層綜合評價值V分別為：V=0.89、V=0.95和V=0.98，則相應評判值區間見表2。

表2 水利工程脆弱性評判等級區間

3 工程案例分析

3.1 工程概況

某中型水庫位于瀾滄江水系南碧河上游，壩址海拔為1 100.0 m，距當地縣城6 km，交通便利，以農田灌溉、工業供水為主，兼顧防洪。水庫徑流面積為47 km2，年均徑流量為482.4萬m3，總庫容為1 236.8萬m3，正常蓄水位為1 098.60 m，設計洪水位為1 099.04 m，校核洪水位為1 099.21 m，工程等別為三等，主、次要建筑物級別分別為3級和4級；設計洪水標準為50年一遇(P=2%)，校核洪水標準為千年一遇(P=0.1%)。

該水庫樞紐工程包括主、副壩、輸水隧洞和溢洪道。水庫設有管理所，負責水庫運行調度管理，機構健全，管理規范，現有管理人員17人，負責水庫工程的日常運行管理工作。在全省水庫的安全評價中，綜合評定該水庫大壩安全等級為三類壩。其中，該水庫工程質量為不合格；運行管理等級為較好；防洪安全復核評價屬于A級；大壩抗滑穩定安全系數存在小于現行規范值，抗滑穩定性差，綜合評價等級為C級；現狀水位情況下，出逸水力坡降均大于允許水力坡降，易于發生滲透變形(流土)破壞，綜合評價滲流安全等級為C級；大壩抗震穩定安全系數均小于現行規范值，綜合評價等級為C級；輸泄水建筑物評價為B級；金屬結構安全評價等級為B級。

3.2 底層基礎指標評價值確定

根據該水庫相關設計資料和安全評估專家報告，以及相關機構對水庫大壩的質量檢測和土工試驗報告，對上述25項評價指標按照定量指標通過計算予以確定，定性指標通過專家打分予以量化的原則，采用定性與定量相結合的方法進行量化，獲得各底層指標的百分制初始值，對其標準化處理后獲得結果見表3。

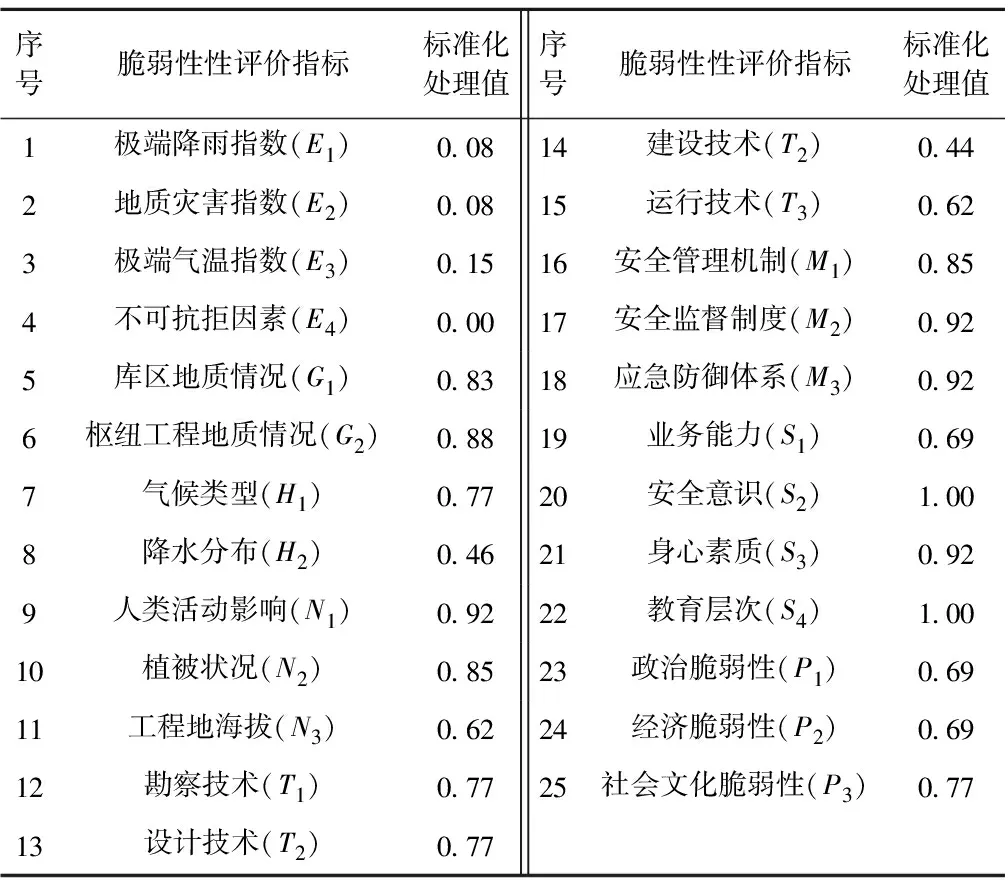
表3 水利工程脆弱性底層指標標準化處理

3.3 歸一化計算

3.3.1原生脆弱性突變分析

根據上文分析原生脆弱性影響因素集可描述為Y={E,G,H,N}，其中E表示突發事件脆弱性，G表示工程地質脆弱性，H表示水文氣象條件脆弱性，N表示自然地理脆弱性。

一級影響因素集：E={E1,E2,E3,E4}，G={G1,G2}，H={H1,H2}，N={N1,N2,N3}

水利工程原生脆弱性的4個控制變量E、G、H和N適用于非互補型的蝴蝶突變模型，其中E1、E2、E3、E4構成互補型蝴蝶突變模型，G1、G2和H1、H2分別構成尖點突變模型，N1、N2和N3適用燕尾突變模型。根據歸一公式，逐級向上層遞歸運算求得各變量的突變級數值為：xE=0.57，xG=0.98，xH=0.94，xN=0.99，由于指標不具有顯著相互關聯性，故適用非互補原則，取最小值，從而得到水利工程原生脆弱性總突變隸屬函數值x(Y)=0.57，相關評判指標及歸一化計算結果見表4所示。

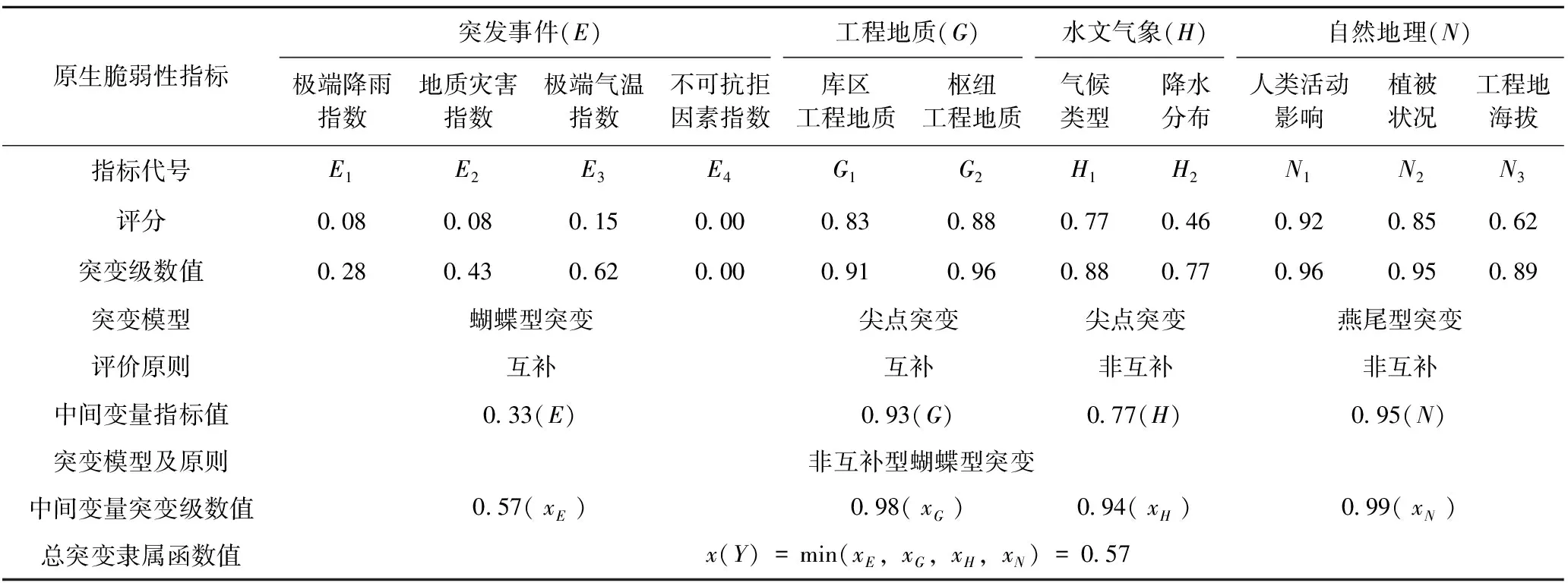
表4 水利工程原生脆弱性評判指標及歸一化計算果

3.3.2水利工程外在脆弱性分析

水利工程外在脆弱性可描述為W={T,M,P,S}，其中T表示技術脆弱性，M表示管理脆弱性，P表示人員脆弱性，S表示社會脆弱性。分別對技術、管理、人員和社會脆弱性的突變過程進行分析計算，得到突變級數值分別為：xT=0.94、xM=0.99、xP=0.98和xS=0.96，根據相應評價原則求得控制變量W的突變隸屬函數值為x(W)=0.94。

3.3.3水利工程脆弱性突變分析

基于上述計算過程，求得水利工程原生脆弱性和外在脆弱性的總突變隸屬函數值分別x(Y)=0.57和x(W)=0.94。由于水利工程脆弱性是水利工程原生脆弱源和外在脆弱源共同作用的結果，故而以Y和W控制變量構建尖點突變模型，求得其相應的突變級數值分別為：xY=0.75、xW=0.98。由于Y和W之間作用結果具有可替代性，因此適用互補原則，取平均值，故水利工程脆弱性的總突變隸屬函數值為x(V)=0.88。相關因素評判指標及歸一化計算結果見表5。

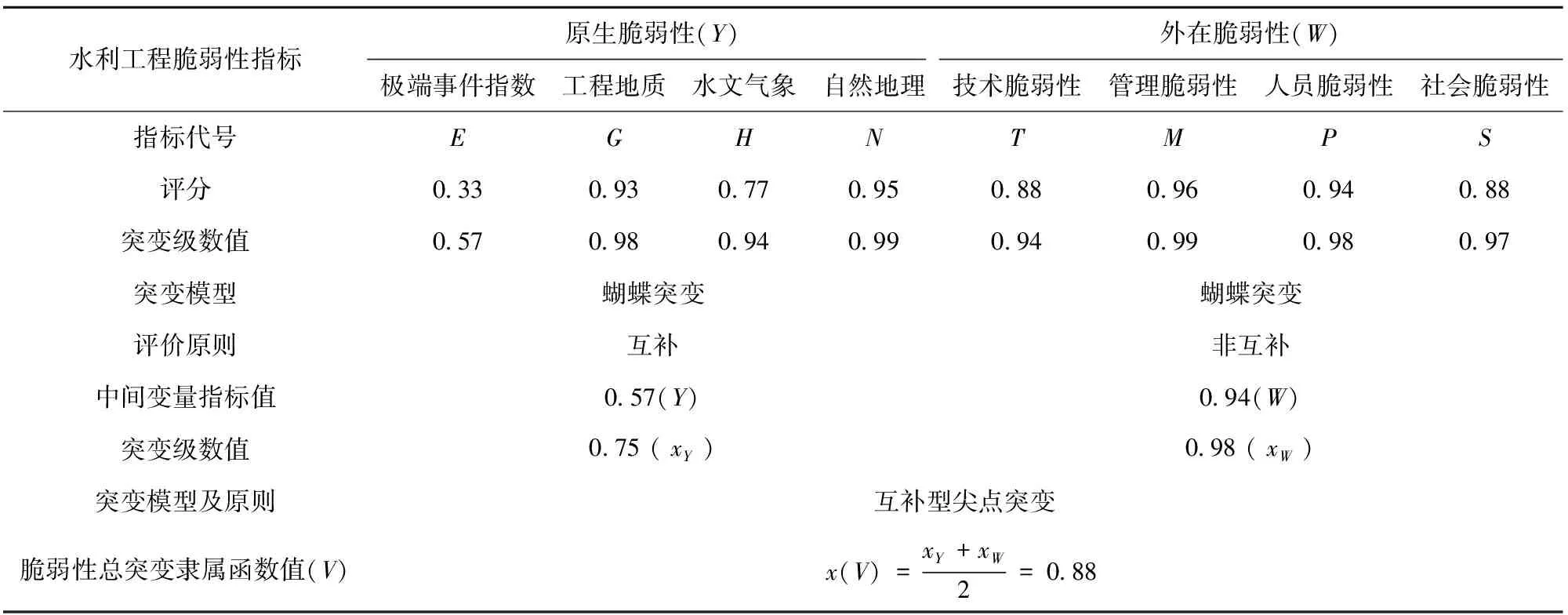
表5 水利工程脆弱性評判指標及歸一化計算

3.4 評價結果分析

根據計算結果，將利工程脆弱性一二級影響指標及其突變級數值列于表6。

1)對照表2所列水利工程脆弱性等級劃分標準可知，該水利工程屬于高度脆弱等級，與上級水利部門出具的安全鑒定評價結果相吻合，證明該評價方法可靠。

2)表6數據顯示，該水利工程原生脆弱性明顯高于外在脆弱性，主要在于考慮了極端事件的影響。在極端氣候環境下，原生脆弱性的破壞作用較外在脆弱性具有更大的破壞力。水利工程原生脆弱性影響因素中自然地理屬于低度脆弱，工程地質狀況屬于中度脆弱，水文氣象條件屬于高度脆弱，基本符合安全鑒定專家報告相關內容。

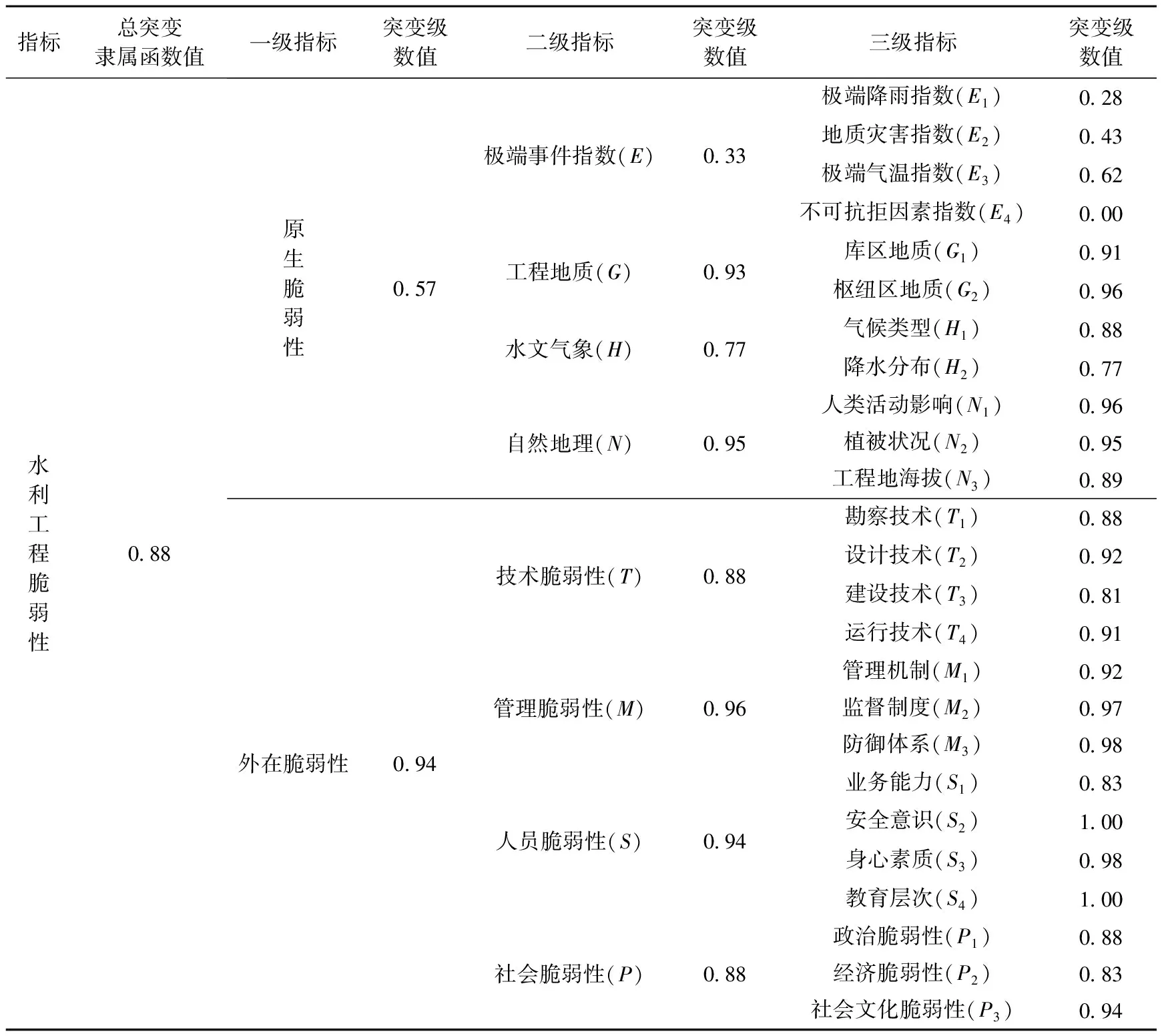
表6 水利工程脆弱性突變評價結果分析

3)表6數據顯示，該水利工程技術脆弱性為高度脆弱，其下級指標勘察技術和建設技術評價值都屬于高度脆弱，運行技術和設計技術指標屬于中度脆弱，說明勘察設計和建設過程中存在重大質量問題，符合水利部門出具的安全鑒定專家報告中工程質量等級為不合格的評價。

4)管理情況屬于低度脆弱，人員狀況處于中度脆弱，社會脆弱性處于高度脆弱狀態，其中社會脆弱性的脆弱源主要反映在經濟脆弱性，說明該工程層存在經濟問題，符合水利部門出具的安全鑒定結果。

4 結語

應用突變理論從原生脆弱性和外在脆弱性兩方面因素對某中型水庫的脆弱性進行評價，最終得到該中型水庫脆弱性等級為高度脆弱，與相關水利部門出具的安全鑒定結果相符，證明該模糊突變模型應用于水庫風險評價有效可行。由于水工建筑形式多樣，其安全類別和評價標準存在差異，從而決定了水利工程脆弱性評價指標的非唯一性和變化性。因此，針對不同類別水利工程的脆弱性評價及其評價指標體系的優化構建，有待于進一步深入研究和探討。同時，為獲取更為準確的評價結果，水利工程管理部門應加強運行管理，建立基于實測資料和工情數據的水利工程脆弱性動態評價和自動預警系統，為水利工程安全管理提供理論依據和決策支持。