基于用戶偏好和項目偏差的創新型科研項目推薦技術研究

贠濤

(中國科學技術交流中心，北京 100045)

0 引言

各種網絡平臺的創新型項目推薦功能能夠使用戶快速獲取有價值的信息，因此對此類技術開展研究十分必要。協同過濾算法在創新型項目推薦技術中的應用非常普遍，但由于沒有充分考慮用戶的個性化需求以及推薦項目間類似元素存在相互干擾的問題，該算法的準確性受到了嚴重的限制。本文提出了一種基于用戶偏好和項目偏差的協同過濾算法(IUCF算法)用于創新型項目推薦，首先進行用戶和項目的聚類再分別計算評分，最后基于二者融合后的預測評分結果實現項目推薦。

1 概論

1.1 用戶評分協同過濾算法

該算法的計算流程為：基于用戶—項目評分矩陣獲取不同用戶的相似度；利用相似度進行相鄰用戶匹配；通過相鄰用戶進行預測評分。選取皮爾森相關系數進行用戶的相似度計算[1]，如式(1)。

(1)

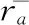
1.2 LDA主題模型

LDA(latent Dirichlet allocation，潛在Dirichlet分布)模型通過Dirichlet概率分布對文本文件的潛在概率進行設定，再通過抽樣算法分別對文本—主題以及主題—詞組的潛在分布進行預估。基于Gibbs采樣的抽樣算法[2]為式(2)。

(2)

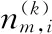
1.3 算法分析

在對創新型項目進行評分預測時，項目間類型較為相近的元素會互相產生干擾進而造成項目偏差，同理，用戶通常是在整個用戶集中選擇近鄰，沒有考慮用戶本質的差異，因而無法明確表達用戶對于項目的個性化需求，此外，用戶的偏好對用戶給出的項目評分存在實際的影響，所以必須以充分挖掘用戶偏好和項目偏差為基礎對創新型項目進行評分。

IUCF(item deviation and user preference combin filtering，項目偏差與用戶偏好組合過濾)算法充分體現了用戶和項目的本質差異，依據用戶本質和項目類別實現聚類，能夠獲得準確的項目偏差分析結果。項目中某類型出現次數的占比與用戶評分矩陣相結合，能夠使出現次數較多的類型獲得對應的高分，從而明確用戶的偏好。

2 算法設計

IUCF算法的模型如圖1所示。

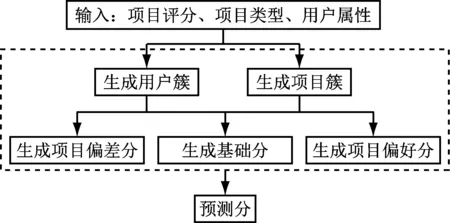
圖1 IUCF算法模型

該算法包含兩個部分，一是分別基于用戶簇和項目簇完成不同類型項目的用戶偏好評分和項目偏差評分，二是利用項目簇中目標用戶對項目的評分均值，通過線性加權處理得到最終的預測評分。

2.1 聚類處理

(1)項目簇創建

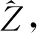
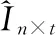
(3)

通過該矩陣的一個行可獲得項目主題簇CNn，通過一個列可獲得主題項目簇CTt[4]，即式(4)。

(4)

式中，CNn為包含項目n的主題的集合；CTt為主題是t的項目的集合；i、j分別為主題號和項目號。

項目n的找尋過程為：首先確定項目所在集合CNn，接下來確定對應每個主題的CTt，通過對CTt的并集處理獲取包含項目n的項目簇Cn，其表達式為式(5)。

(5)

(2)用戶簇創建

用戶的職業、性別、年齡都可以作為用戶的屬性元素。設Q為用戶的集合，Q={Q1，…，Qi}，Qi為第i個用戶，每個用戶的屬性集合為Qi={q1，…，qk}，qk為i用戶所具有的第k個屬性。

K-means聚類應以用戶基本屬性的預處理為前提，其過程以通過對具體的屬性進行編碼分組實現。對于性別，以數字1和2分別代表男性和女性；對于年齡，可通過劃分不同的年齡段進行分組，其中，1—80歲人群以20歲為間隔創建編號1—4的四個組，80歲以上人群全部劃入5號組；對于職業，首先對所有用戶的職業進行分類，再明確各種職業所對應的用戶數量，根據成組元素二八定理的重要性權重理論，將用戶數量排名屬于前20%的職業分別編入1—4號組，剩余職業全部編入5號組。按照上述方式分組后，用戶屬性集合Qi即可通過數字編碼表示。

鑒于K-means聚類具有無監督學習的特征，本文選用簇內曲線拐點聚類法基于SSE(sum of squares errors，誤差平方和)確定聚類的實際數量。K-means聚類的結果即為包含用戶a的用戶簇Ua，即式(6)。

Ua={uj|uj∈Q,j∈[1,i]}

(6)

式中，uj為用戶簇所包含的第j個用戶。

2.2 項目偏差分計算

分別基于用戶簇和項目簇對用戶和項目進行過濾，通過單個項目得分與所有項目平均得分的差值來量化項目偏離的程度。具體的計算過程如下。

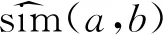
(7)

(2)在用戶簇中，計算目標用戶與其余用戶的放大相似度，篩選出與目標用戶a相關性最強的k個用戶作為其最近鄰,為式(8)。

(8)

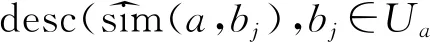
(3)在用戶簇中，用戶a對項目n的項目偏差IDan分由加權平均偏差表示，即式(9)。

(9)

2.3 用戶偏好分計算

用戶偏好分表達了用戶對各種項目的主觀偏好，能夠彌補評分項過少的情況下項目偏差分調節能力不足的缺陷，具體的計算過程如下。

(1)通過用戶類型偏好明確用戶類型喜好，用戶偏好分是某一類型在所有類型的總評分中所做出的貢獻占比，即式(10)。

(10)

式中，pai為用戶a對第i個類型的用戶偏好分；sai為用戶a對第i個類型的打分次數；paj為用戶a對項第j個類型的評分；m、n分別為類型數量和項目數量。sai為用戶—類型評分矩陣Sa×m內的所有項，Sa×m的獲取方法為式(11)。

(11)

z-score標準化能夠體現單項值與平均值差距的大小，該數值的正負說明了用戶對類型的喜好，即喜歡或不喜歡，用戶類型偏好分的z-score標準化處理方式為式(12)。

(12)

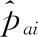
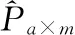
(13)

式中，dit為矩陣Dm×t的第m個類型與第t個主題相對應的概率；Nn為主題簇CNn中主題的總數量。

2.4 綜合預測評分

在包含創新型項目的項目簇初始評分均值的基礎上，加入用戶偏好分和項目偏差分即可得到該項目的綜合預測評分。引入權重系數λ調節用戶偏好分和項目偏差分，則用戶a對項目n的綜合預測評分Tan的計算方式為式(14)。

(14)

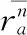
3 實驗驗證

實驗采用國外某知名高校所建立的Movielens100k數據集，其中包含943位用戶對1 682個創新型項目的預測評分以及用戶的屬性和項目的類型。從數據集中選取80%的數據進行評分訓練，其余部分用以評分測試。

3.1 實驗指標

實驗結果的準確性通過MAE(平均絕對誤差)進行衡量，其計算方式為式(15)。

(15)

式中，N為預測項目的數量。MAE值越小則項目推薦的準確性越高。

3.2 參數確定實驗

(1)K-means聚類數量

基于肘方法分別代入2—8七個數值作為待定聚類數量，計算出每個數值對應的SSE，計算結果如圖2所示。

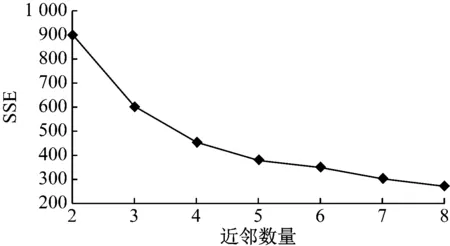
圖2 不同聚類數量下SSE的計算結果

由圖2可見，SSE的值隨聚類數量的增多而減小，聚類數量由2增加到3時，SSE的減幅為約為300，且自此之后的減幅均比第一次調整小，可見聚類數量為3時對應的坐標點即為簇內曲線拐點聚類法的拐點，因此能夠確定最佳聚類數量為3。

(2)LDA聚類主題數量

設定λ=1，由式(14)可知此時預測評分僅受項目偏差分的影響，因此可以快速確定最合適的主題數量。將近鄰數量設定為10、30、50，基于Gibbs抽樣方法分別代入12—18七個數值作為待定主題數量，同時根據文獻[1]的實踐設定a=50/T，β=0.01，計算結果如圖3所示。

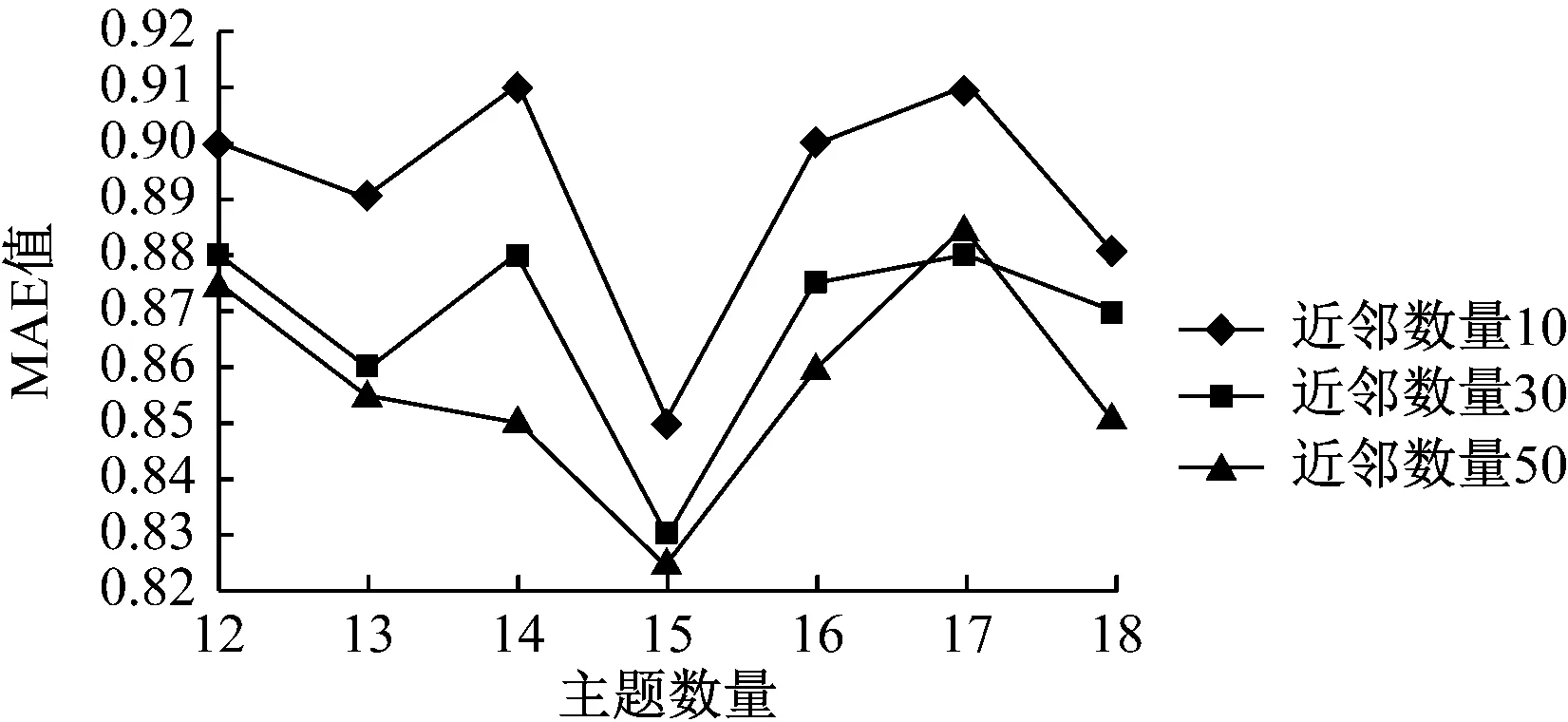
圖3 不同主題數量下MAE的計算結果

由圖3可見，在設定的3種近鄰數量條件下，MAE值均在主題數量為15時為最小，因此可以確定最佳LDA聚類主題數量為15。

(3)權重系數λ

將近鄰數量設定為10、30、50，反復對權重系數λ的值進行調整，通過IUCF算法所得的MAE值，如圖4所示。

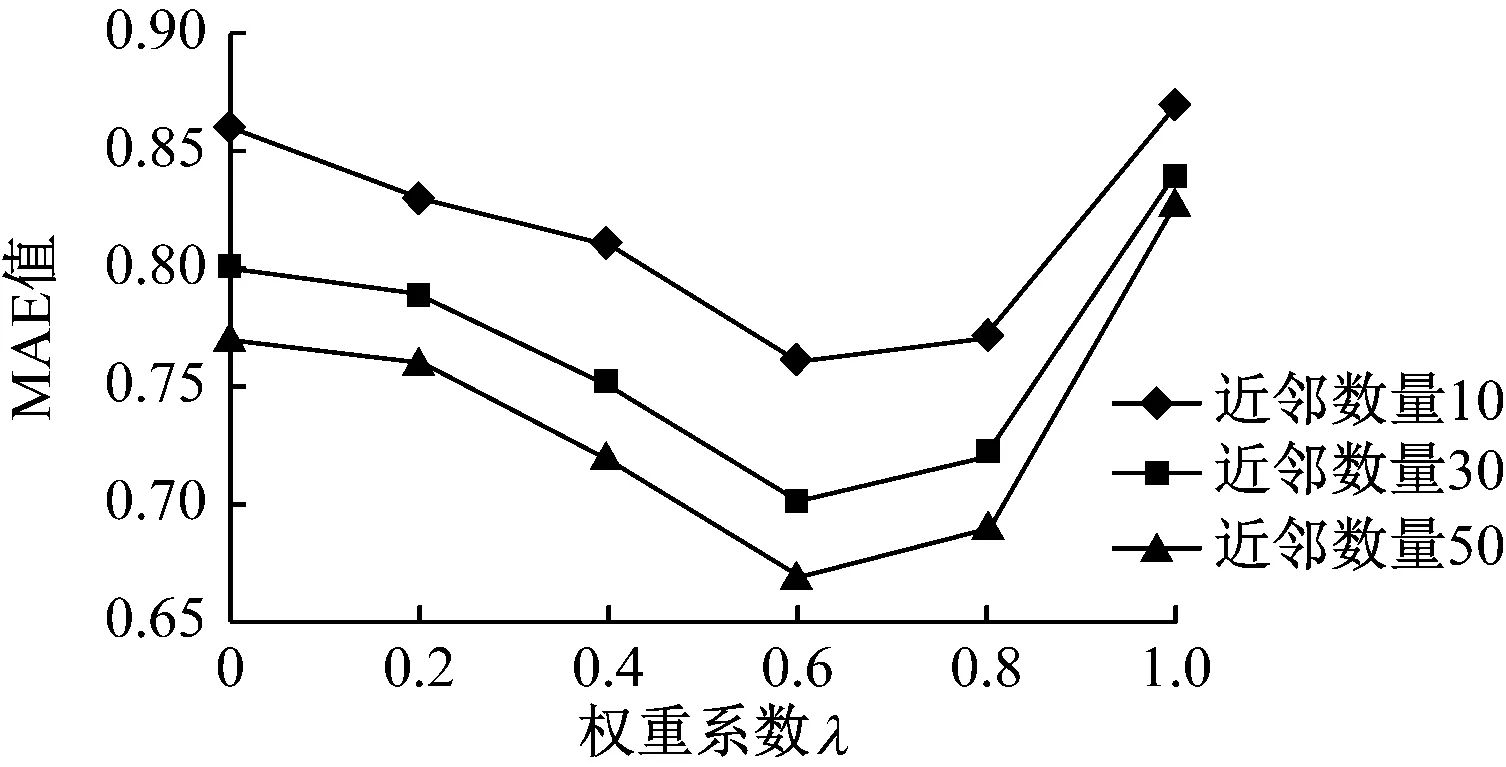
圖4 不同權重系數下MAE的計算結果

由圖4可見，在設定的3種近鄰數量條件下，MAE值均在λ=0.6時為最小，因此可以確定權重系數λ的最佳取值為0.6。

3.3 對比實驗

為了驗證本文所提出的IUCF算法在準確度方面是否具有優勢，選取常規協同過濾算法UCF[2]、基于項目類型的協同過濾算法ICF[3]、基于概率矩陣分解和特征轉移的推薦算法FTMF[4]以及基于安全網絡的協同過濾算法ECFATN[5]共4種算法與本算法進行準確度對比，實驗結果如圖5所示。

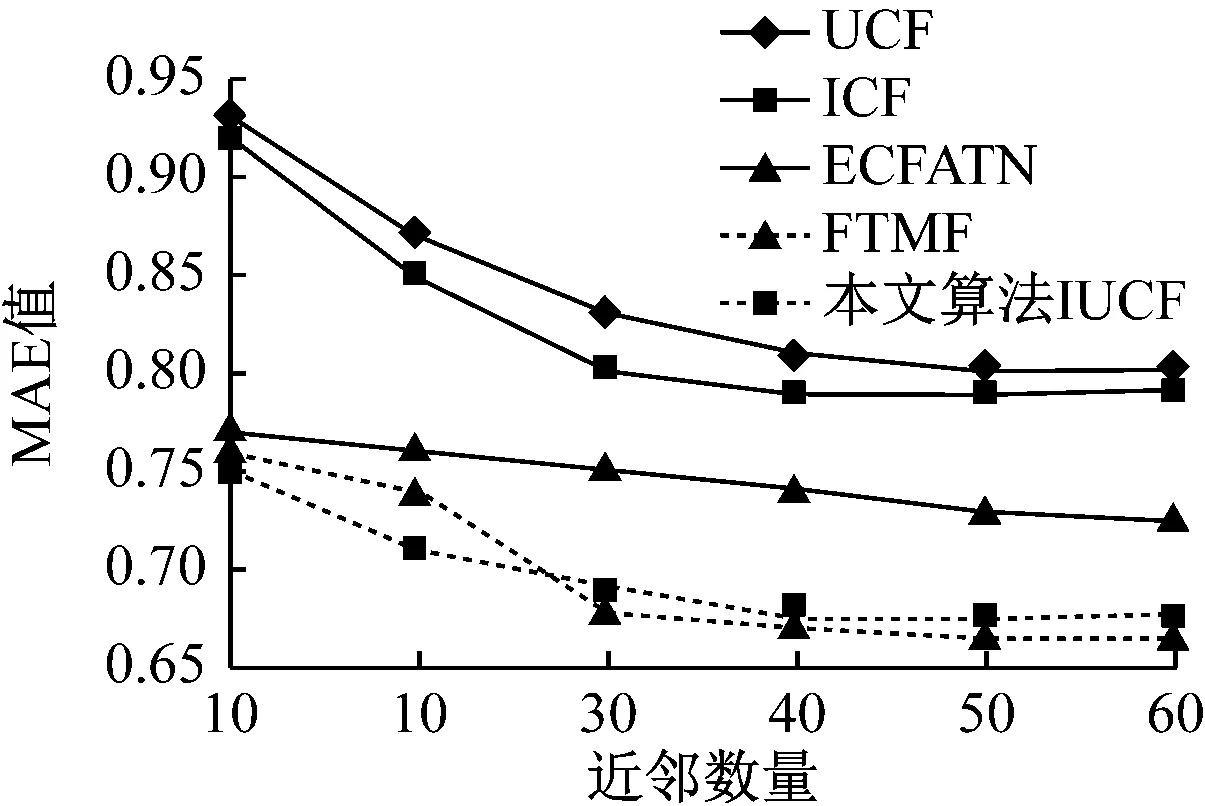
圖5 不同算法的MAE值對比結果

由圖5可見，通過IUCF算法所得的MAE值低于UCF、ICF與FTMF 3種算法，說明IUCF算法相較于其它協同過濾算法能夠實現更準確的推薦。在不同近鄰數量的條件下，IUCF算法的MAE值低于ECFATN算法，但近鄰數量達到30以上時，MAE值較FTMF算法高，分析認為可能是近鄰數量過多造成的，而只要近鄰數量少于30，IUCF算法的MAE值均低于FTMF算法，可見在近鄰數量不多于30的條件下IUCF算法的準確度是具有優勢的。

4 總結

為了解決創新型項目推薦技術原有算法準確度受限的問題，本文提出了一種基于用戶偏好和項目偏差的IUCF算法，介紹了算法的實現機制，闡述了算法的設計過程，通過實驗確定了算法關鍵參數的最佳取值，并通過與其它算法的對比驗證了IUCF算法在創新型項目推薦方面所具備的高準確度的優勢。本文所設計的算法有效解決了用戶與項目間類似元素互相干擾所造成的準確度較低的問題，目前已應用于國內人口年齡組劃分新方法的研究項目并發揮了顯著的作用，具有很強的實用性。