考慮非高斯相關噪聲的視線角速率提取算法

張鐸，宋建梅，趙良玉,*，焦天峰，丁國強

1.北京理工大學 宇航學院，北京 100081 2.中國兵器工業導航與控制技術研究所，北京 100089 3.鄭州輕工業大學 電氣信息工程學院，鄭州 450002

捷聯導引頭因性能可靠、結構簡單、成本低廉等優勢，在空空導彈、反坦克導彈、制導炮彈、制導火箭彈等戰術武器領域具有廣闊而明確的應用需求。但是，由于捷聯導引頭只能敏感到目標與彈體軸線方向的角度關系，無法直接獲取諸多戰術武器制導所需的視線角速率信息。為了解決捷聯導引頭的視線角速率提取問題，國內外專家學者開展了廣泛而深入的研究，并取得了豐富的研究成果。

姚郁和章國江[1]在將視線角與彈體姿態進行解耦的基礎上，實現了捷聯成像導引頭視線角速率的提取。文獻[2]建立了以視線高低角、視線高低角速率、視線方位角和視線方位角速率為狀態變量的視線角速率估計模型以及全捷聯導引頭解耦模型，提出了基于擴展卡爾曼濾波(Extended Kalman Filter，EKF)的視線角速率提取算法。文獻[3]提出了基于無跡卡爾曼濾波(Unscented Kalman Filter，UKF)的視線角速率提取算法，得到了更高的估計精度。文獻[4]對狀態變量進行擴充，增加了導彈與目標相對距離及其距離變化率兩個狀態變量，并利用五階容積卡爾曼濾波(Cubature Kalman Filter，CKF)算法提取視線角速率，得到了較高的估計精度，但是彈目相對距離與彈目相對距離變化率這兩個狀態變量在只有角度觀測情況下存在觀測性弱的問題，對狀態的估計精度和算法的穩定性會造成不利影響。文獻[5]中提出了基于機載平臺的修正球面坐標系目標跟蹤模型，有效地改善了觀測性弱的問題。文獻[6]提出了修正極坐標系下的雷達與電子支援措施航跡對準關聯算法，實現了雷達與目標之間的穩定追蹤。上述研究均假設狀態噪聲與觀測噪聲為高斯白噪聲且它們之間相互獨立，這與真實場景下狀態噪聲和觀測噪聲的統計特性并不完全相符。

針對非高斯噪聲條件下的視線角速率提取問題，文獻[7-9]均采用粒子濾波(Particle Filter，PF)來提高視線角速率的估計精度，但是粒子濾波隨著迭代次數的增加，容易出現由于權重過度集中而導致的粒子退化現象。文獻[10]提出了應用于紅外圖像導引頭的視線角速率提取分層采樣粒子濾波算法，有效解決了粒子退化現象，但是增加了系統計算負擔。文獻[11]提出了基于自適應預測濾波的視線角速率提取算法，利用不斷變化的殘差對噪聲方差進行在線調整，提高了對非高斯噪聲的濾波性能。由于集員濾波算法不需要已知噪聲的分布特性，故在非高斯噪聲環境下的視線角速率提取方面展現出良好的應用前景。集員濾波算法最初由Schweppe[12]于1968年提出。Maksarov[13]、Kurzhanski[14]和Chernousko[15]等進一步發展了針對狀態和參數估計的橢球計算方法。Scholte和Campbell[16]利用區間估計方法建立了非線性系統的擴展集員濾波(Extended Set Membership Filter，ESMF)算法。文獻[17]拓展了集員濾波在故障檢測領域中的應用，利用次最小容積法則實現狀態橢球與觀測橢球的更新計算，提出了基于擴展橢球集員濾波的故障檢測與隔離算法。文獻[18]提出了一種基于MIT(Massachusetts Institute of Technology)規則的自適應擴展集員濾波算法，其利用MIT優化規則對狀態噪聲橢球進行自適應選取，實現了更快的健康度恢復速率。文獻[19]提出了基于純方位目標跟蹤的外定界橢球集員估計算法，該算法采用最小化后驗估計誤差的李雅普諾夫函數上界的策略來獲得觀測更新橢球，能夠更加合理地利用觀測信息，并降低了運算量。

然而，以上這些考慮非高斯噪聲的濾波算法均建立在狀態噪聲與觀測噪聲相互獨立的前提下，沒有考慮狀態噪聲與觀測噪聲的相關性對估計結果的影響。由于導彈在飛行過程中存在大量不確定的干擾因素[20-21]，例如機械振動以及彈體彈性形變等。這些客觀因素使得狀態噪聲與觀測噪聲相互獨立的假設難以保證[22]。為此，本文圍繞考慮相關噪聲解耦的視線角速率提取算法開展研究，推導了基于修正球面坐標系的視線角速率提取模型，建立了視線角速率提取模型的相關噪聲解耦方法以及解耦后模型的線性化表達式，得到了相關噪聲解耦的擴展橢球集員濾波算法，并以某型搭載捷聯導引頭的制導火箭彈為例進行了仿真驗證。

1 修正球面坐標系下的視線角速率提取模型

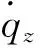
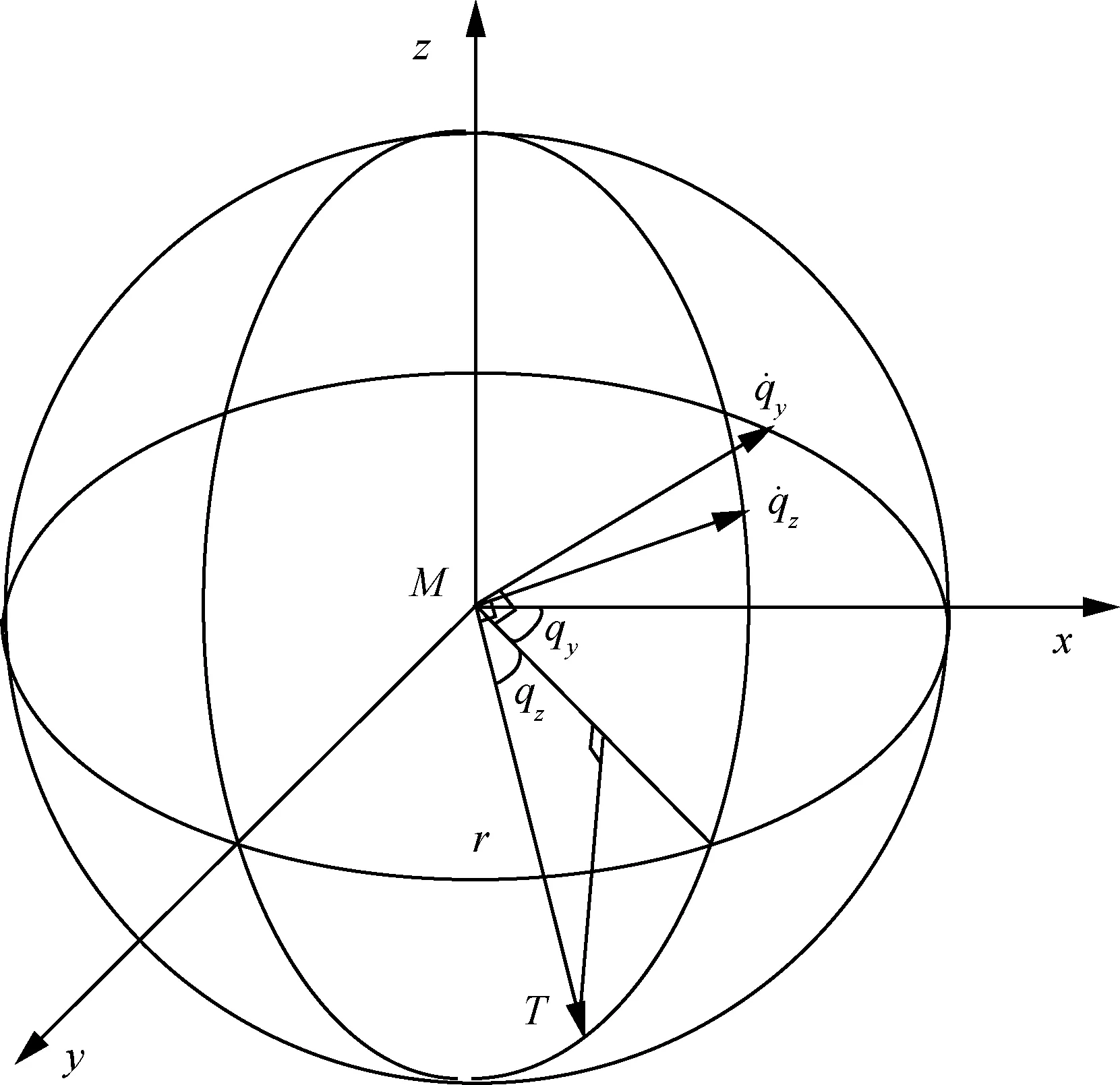
圖1 彈目相對位置關系

根據球面坐標系下的彈目相對位置關系可以得到彈目相對運動方程為[2]

(1)

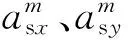
(2)

(3)

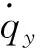
(4)

(5)

(6)

(7)

由彈目相對運動模型式(1)可知

(8)

將式(8)代入式(7)并化簡得到

(9)

(10)

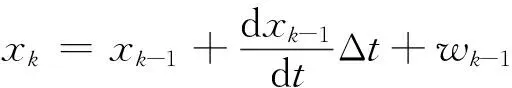
(11)

式中：Δt為采樣時間間隔；wk-1為包含離散化誤差的狀態噪聲項。

由于目標在視線坐標系和體視線坐標系中的坐標均為(r,0,0)，則經過坐標轉換得到目標在彈體坐標系和地面坐標系內的投影分別為

(12)

(13)

(14)

聯立式(12)～式(14)并整理得到視線角解耦模型為[3]

(15)

(16)

式中：γ、?和ψ分別為導彈的滾轉角、俯仰角和偏航角。選取捷聯導引頭測得的體視線高低角qα和體視線方位角qβ為觀測量，可以得到觀測方程為

(17)

2 考慮相關噪聲解耦的擴展橢球集員濾波算法

在第1節所建立視線角速率提取模型與視線角解耦模型的基礎上，針對狀態與觀測模型中存在非高斯相關噪聲的情況，根據文獻[23]中對高斯噪聲假設條件下相關噪聲的處理方法，利用集員濾波中橢球形狀矩陣與Kalman濾波中的噪聲協方差矩陣作用相似的特性，用非高斯噪聲的橢球形狀矩陣代替相關噪聲解耦框架中的噪聲協方差矩陣，對觀測模型中的相關噪聲進行解耦，在此基礎上運用擴展橢球集員濾波算法，實現對非高斯相關噪聲的濾波計算。將第1節所建立的狀態模型式(10)和觀測模型式(17)簡寫為

(18)

wk-1∈Ω(0,Qk-1),vk∈Ω(0,Rk)

(19)

式中：Qk-1為狀態噪聲橢球的形狀矩陣；Rk為觀測噪聲橢球形狀矩陣，可以將每一時刻的狀態分布情況按照橢球集合定義為

Ω(a,P)={x∈Rn|(x-a)TP-1(x-a)≤1}

(20)

i=1,2,…，n

(21)

對式(18)中的觀測方程做變換[22]：

(22)

式中：G為待求矩陣，對式(22)中包含狀態變量的項和噪聲項分別進行合并，得到

h*(xk)=h(xk)+G(xk-f(xk-1))

(23)

(24)

則觀測噪聲協方差矩陣，即觀測噪聲橢球形狀矩陣可以轉換為

(25)

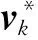
Sk-Qk-1GT=0

(26)

由式(26)得到待求矩陣G的表達式為

(27)

將式(27)代入式(25)得到解相關性的觀測噪聲橢球形狀矩陣為

(28)

同理，將式(27)代入式(23)得到解相關性的觀測函數為

(29)

由此得到相關噪聲解耦的視線角速率提取算法狀態方程與觀測方程為

(30)

對相關噪聲解耦之后的狀態模型與觀測模型開展擴展橢球集員濾波算法的推導。對式(30)中的狀態方程進行線性化變換，對k-1步的狀態變量xk-1通過一階泰勒級數來逼近第k步的狀態變量預測值xk：

(31)

(32)

式中：Hf1,Hf2,…,Hfn為狀態函數關于每個狀態變量的海森矩陣(Hessian Matrix)。將狀態方程的拉格朗日余項作為其誤差的一部分來考慮，式(31)可以簡化為

(33)

(34)

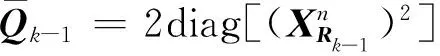
同理可以得到解相關性觀測方程的線性化表達式為

(35)

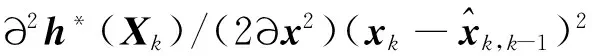
(36)

式中：Hh*1,Hh*2,…,Hh*n為解相關性觀測函數關于每個狀態變量的海森矩陣。同理，把解相關性觀測方程的拉格朗日余項作為誤差的一部分來考慮，式(35)可以簡化為

(37)

(38)

(39)

利用橢球集員濾波算法計算時間更新的狀態橢球邊界為

(40)

(41)

觀測更新為

(42)

(43)

(44)

其中：

(45)

(46)

F和H分別為狀態方程的系數矩陣和解相關性的觀測方程系數矩陣；βk和ρk分別為時間更新橢球和觀測更新橢球的調節尺度因子；δk為算法健康度因子，當狀態橢球或觀測噪聲橢球無效時δk≥1，其表達式為

(47)

尺度因子參數的求解涉及到兩個橢球直和運算得到的外包橢球最優化問題，對βQk-1、βRk和βk-1的計算選取外包橢球的最小跡計算方法，該方法求解形式簡單，且與外包橢球最小化體積的優化準則相比，該方法魯棒性更強，計算量更小。根據橢球最小跡法則有

β=argmin tr(P)

(48)

從而可以根據

(49)

獲得最優的尺度因子參數，其中：P1和P2為任意兩個橢球形狀矩陣。

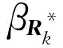
(50)

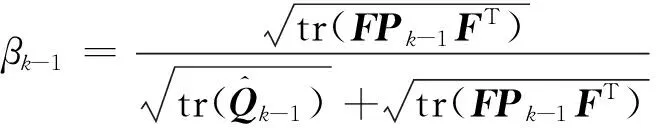
(51)

考慮觀測更新的橢球形狀矩陣計算公式為

(52)

在迭代計算過程中，觀測更新的橢球形狀矩陣的形式往往較為復雜，導致Pk計算復雜度較高，無論采用最小化橢球體積法還是橢球最小跡法，尺度因子參數ρk的優化計算都很困難，甚至無法獲得解析解。采用最小化性能指標δk的上界形式來計算，可以大大降低計算成本，根據：

ρk=argmin sup(δk)

(53)

得到尺度因子ρk的次優計算公式為

(54)

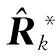
3 案例研究

本文選用裝載捷聯導引頭的某型遠程制導火箭彈的末制導仿真對算法進行驗證，利用彈道仿真獲得的火箭彈加速度與姿態數據實時更新狀態模型與觀測模型，根據比例導引律將視線角速率的提取結果實時進行導引，控制火箭彈精確命中目標。設置仿真初始時刻參數如表1 所示。

表1 初始仿真狀態

選取球面坐標系下狀態模型的初始值為

x0=[-0.917 5,-0.009 5,0,0,18 890,-611]T

修正球面坐標系下狀態模型的初始值為

xMSC0=[-0.917 5,-0.009 5,0,0,5.293 8×

10-5,-0.032 3]T

對比兩種模型初始值可以看出，修正球面坐標系模型在經過規范化處理以后，實現了狀態變量從有量綱到無量綱的轉換，便于后續的迭代計算。為了驗證修正球面坐標系下視線角速率提取模型的性能，對修正球面坐標系下的視線角速率提取模型與傳統球面坐標系下的視線角速率提取模型的估計精度進行對比分析。假設狀態噪聲與觀測噪聲均為高斯白噪聲，且相互獨立，其中觀測噪聲的均方根誤差為0.035 rad。在初始條件相同的情況下，采用EKF算法分別進行仿真的結果如圖2和圖3所示。

圖2 球面坐標系模型與修正球面坐標系模型視線高低角與視線高低角速率估計曲線

圖3 球面坐標系模型與修正球面坐標系模型視線方位角與視線方位角速率估計曲線

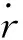
在修正球面坐標系模型的基礎上，假設狀態噪聲與觀測噪聲為相互獨立且滿足均勻分布的非高斯噪聲，其中觀測噪聲形狀矩陣根據式(19)定義為分別采用ESMF算法和PF算法進行視線角速率提取，得到的仿真結果如圖4和圖5所示。

圖4 ESMF與PF算法視線高低角及其角速率估計曲線

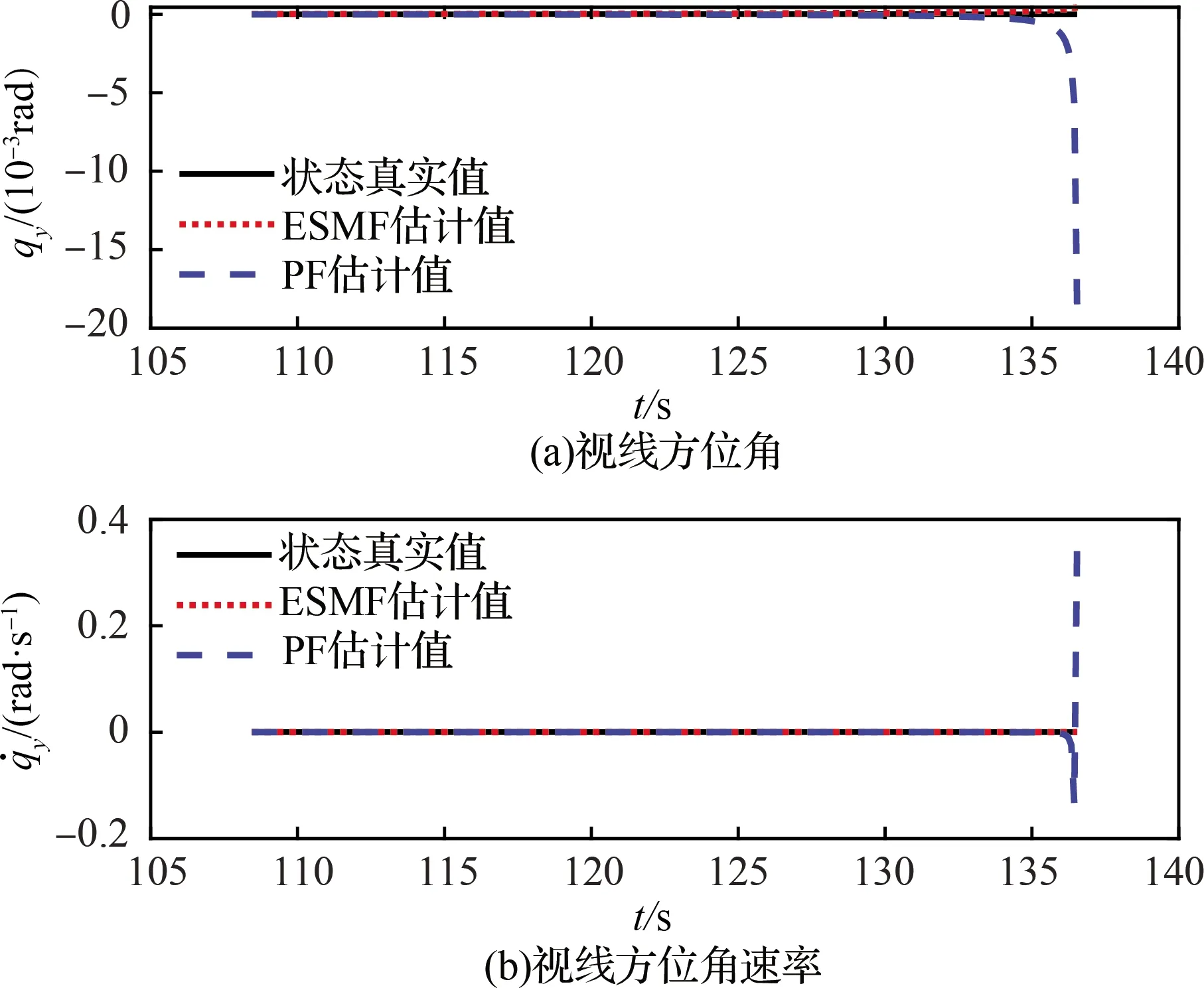
圖5 ESMF與PF算法視線方位角及其角速率估計曲線

可以看出，在非高斯噪聲條件下，PF算法得到的視線角及視線角速率的估計結果在后半段出現了嚴重發散，導致估計結果與真實狀態之間的誤差迅速擴大，無法提供可用的制導信息。反觀ESMF算法，由于不需要已知觀測噪聲和狀態噪聲的分布情況，僅要求噪聲有界，表現出更好的魯棒性。此外，ESMF算法將線性化誤差項與模型本身的噪聲項通過直和計算引入到虛擬噪聲橢球中，充分考慮了線性化誤差對模型估計結果的影響，故該算法得到的視線角與視線角速率估計精度高于PF算法，最大誤差僅為0.01 rad/s，能夠滿足高精度比例導引制導的需要，是一種更符合工程應用且精度較高的濾波方案。

針對噪聲相關且非高斯的情況，假設狀態噪聲與觀測噪聲滿足均勻分布，視線高低角與體視線高低角、視線方位角與體視線方位角存在相關性，令狀態噪聲與觀測噪聲的相關性矩陣為開展相關噪聲解耦的ESMF算法仿真，與相關噪聲未解耦ESMF算法的仿真結果如圖6和圖7所示。可以看出，未進行相關噪聲解耦的ESMF算法得到的估計結果已經不能很好地跟蹤狀態真實值，且估計結果在末端出現不同程度的發散，其中，視線方位角速率的末段估計誤差達到了0.05 rad/s以上。而采用相關噪聲解耦算法得到的視線方位角速率與視線高低角速率的估計精度較高，在末段誤差最大僅為0.005 rad/s，能夠更好地跟蹤狀態真實值，實現了在非高斯相關噪聲條件下對捷聯導引頭視線角速率的高精度估計。

圖6 相關噪聲解耦與未解耦狀態下視線高低角及其角速率估計曲線

圖7 相關噪聲解耦與未解耦狀態下視線方位角及其角速率估計曲線

4 結 論

1)通過對傳統球面坐標系下的彈目距離及其變化率進行規范化處理，建立了修正球面坐標系下的視線角速率提取模型，經過仿真驗證，該模型具有更高的估計精度以及更好的數值穩定性。

2)提出利用相關噪聲解耦的ESMF算法解決捷聯導引頭的視線角速率提取問題，經過仿真驗證，在模型中存在均勻噪聲的條件下，其視線角速率的估計誤差不大于0.005 rad/s，視線角的估計誤差不大于0.01 rad，說明所提出的算法在典型非高斯相關噪聲情況下具有良好的濾波精度，對于其他非高斯噪聲條件下的濾波效果尚需進一步研究。