無(wú)人機(jī)用燃料電池陰極供氣系統(tǒng)建模與控制

趙冬冬，趙國(guó)勝，夏磊，方淳，馬睿，皇甫宜耿

1.西北工業(yè)大學(xué) 自動(dòng)化學(xué)院，西安 710129 2.航空工業(yè)第一飛機(jī)設(shè)計(jì)研究院，西安 710089

燃料電池是一種通過化學(xué)反應(yīng)，將化學(xué)能轉(zhuǎn)變?yōu)殡娔艿男滦桶l(fā)電裝置[1-2]，目前研究的燃料電池有固體氧化物燃料電池、熔融碳酸鹽燃料電池和質(zhì)子交換膜燃料電池(PEMFC)等多個(gè)類型[3]，其中，PEMFC因其效率高、噪聲小、排放無(wú)污染等優(yōu)點(diǎn)，被認(rèn)為是未來最具有潛力的無(wú)人機(jī)用動(dòng)力源，成為當(dāng)前的研究熱點(diǎn)[4-6]。PEMFC系統(tǒng)通常包含空氣供應(yīng)子系統(tǒng)、氫氣供應(yīng)子系統(tǒng)、濕度控制子系統(tǒng)、溫度控制子系統(tǒng)和功率調(diào)節(jié)子系統(tǒng)5部分。其中，陰極空氣供應(yīng)子系統(tǒng)由空壓機(jī)、驅(qū)動(dòng)電機(jī)、供氣歧管、返回歧管等多個(gè)部分構(gòu)成[7]，空壓機(jī)提供的氧氣流量及陰極氧氣分壓是決定PEMFC系統(tǒng)效率和動(dòng)態(tài)性能的關(guān)鍵因素[8]。

無(wú)人機(jī)飛行過程中，由高度變化引起的氣壓變化、溫度變化、濕度變化和氧含量變化等，會(huì)直接影響到空壓機(jī)的工作特性，進(jìn)而對(duì)燃料電池的工作性能產(chǎn)生影響[9-10]。另一方面，無(wú)人機(jī)飛行狀態(tài)的變化會(huì)直接導(dǎo)致燃料電池負(fù)載的變化，在燃料電池的加載過程中，能否及時(shí)根據(jù)負(fù)載的變化對(duì)陰極供給流量以及陰極壓力做出調(diào)整，將會(huì)直接影響到燃料電池的工作性能[4]。因此，要保證燃料電池系統(tǒng)的高效率和可靠性，對(duì)變高度下空壓機(jī)的特性以及陰極供氣系統(tǒng)的研究具有重要意義。

空壓機(jī)模型一般可通過對(duì)大量不同工況下的空壓機(jī)實(shí)驗(yàn)數(shù)據(jù)擬合得到，但由于空壓機(jī)試驗(yàn)條件的限制，在全運(yùn)行范圍內(nèi)的實(shí)驗(yàn)數(shù)據(jù)往往非常有限。此外，查找表的插值程序不是連續(xù)可微的，尤其在實(shí)驗(yàn)數(shù)據(jù)有限的情況下，外推不可靠，查找表的預(yù)測(cè)性會(huì)大大降低。Deng等[11]基于數(shù)據(jù)驅(qū)動(dòng)建立了外源輸入的非線性自回歸移動(dòng)平均(NARMAX)空壓機(jī)模型，并采用循環(huán)神經(jīng)網(wǎng)絡(luò)(RNN)方法估計(jì)模型參數(shù)。但空壓機(jī)進(jìn)口工況存在很強(qiáng)的相關(guān)性，入口溫度與壓力的變化會(huì)影響入口氣體密度和流量的大小，增加了在全轉(zhuǎn)速、變高度下神經(jīng)元的訓(xùn)練難度。CFX、Fluent以及Numeca等軟件通過計(jì)算流體動(dòng)力學(xué)(CFD)的數(shù)值模擬方法模擬空壓機(jī)輸出性能，但該方法計(jì)算量大，結(jié)果可信度和計(jì)算精度都有待提高[12]。偏最小二乘法(PLS)回歸算法是一種由化學(xué)領(lǐng)域發(fā)展形成的新型數(shù)據(jù)統(tǒng)計(jì)分析方法，其在預(yù)測(cè)空壓機(jī)性能方面具有強(qiáng)魯棒性，需要的數(shù)據(jù)量少且具有明顯物理意義的優(yōu)點(diǎn)。Li等[13]在傳統(tǒng)PLS模型的基礎(chǔ)上，使用冪函數(shù)多項(xiàng)式或三角函數(shù)多項(xiàng)式作為基函數(shù)(PLSN)，預(yù)測(cè)離心空壓機(jī)的壓比和效率，PLSN在計(jì)算時(shí)間最短的情況下預(yù)測(cè)精度最高，模型結(jié)構(gòu)也更加簡(jiǎn)單。但PLSN方法并不是對(duì)所有的多重共線性問題都有效，某些數(shù)據(jù)處理的結(jié)果會(huì)對(duì)空壓機(jī)的建模影響較大。Gravdahl[14]和Chu[15]等在地面常溫常壓條件下，基于熱力學(xué)第一定律，從能量傳遞的角度提出了一種能夠在虛擬實(shí)驗(yàn)臺(tái)(VTB)計(jì)算環(huán)境中進(jìn)行系統(tǒng)仿真的離心式空壓機(jī)動(dòng)態(tài)模型。本文基于文獻(xiàn)[14-15]中的方法預(yù)測(cè)摩擦損失，同時(shí)考慮了不同高度下溫度、氣壓、密度、雷諾數(shù)等環(huán)境因素變化，建立了適用于不同高度下的空壓機(jī)模型。

無(wú)人機(jī)飛行狀態(tài)的改變會(huì)導(dǎo)致燃料電池負(fù)載的劇烈變化，當(dāng)負(fù)載突變時(shí)，如果不能根據(jù)負(fù)載電流的變化，及時(shí)對(duì)進(jìn)入陰極的空氣流量做出調(diào)整，則會(huì)出現(xiàn)氧饑餓或氧飽和現(xiàn)象。氧饑餓現(xiàn)象的發(fā)生會(huì)導(dǎo)致燃料電池輸出電壓及功率的降低，嚴(yán)重時(shí)更會(huì)影響燃料電池的壽命[16]。氧飽和現(xiàn)象的發(fā)生則會(huì)導(dǎo)致功率的浪費(fèi)，進(jìn)而降低燃料電池系統(tǒng)的效率[17]。為避免氧饑餓和氧飽和現(xiàn)象的發(fā)生，一些文章中提出了根據(jù)負(fù)載變化對(duì)PEMFC陰極過氧比(空壓機(jī)提供的氧氣量與燃料電池實(shí)際反應(yīng)所需的氧氣量之比)的控制。Zhang[18]和Baroud[19]等給出了PEMFC陰極供氣系統(tǒng)的四階模型，并基于所給模型，針對(duì)過氧比的控制提出了不同的模糊PID控制算法。劉秋秀[20]采用半機(jī)理半實(shí)驗(yàn)建模的方法給出了PEMFC九階供氣系統(tǒng)模型，并提出了基于系統(tǒng)傳遞函數(shù)的一階最優(yōu)自抗擾控制(ADRC)控制策略。王帥[21]給出了四階供氣系統(tǒng)模型，并考慮了空壓機(jī)電壓不能無(wú)限制增加的因素，提出了具有約束處理能力的模型預(yù)測(cè)控制(MPC)。李克雷[22]和郭愛[23]等為保持燃料電池系統(tǒng)凈輸出功率最大，提出了針對(duì)過氧比的電堆電流前饋控制和空氣流量模糊反饋控制的策略。浙江大學(xué)Chen等[3]給出了陰極供氣系統(tǒng)的三階模型，并基于反饋線性化的方法設(shè)計(jì)了一個(gè)非線性控制器來跟蹤控制過氧比保持在最優(yōu)值。Zhang等[24]針對(duì)燃料電池供氣系統(tǒng)過氧比提出了一種基于2型模糊邏輯系統(tǒng)(T2-FLS)的自適應(yīng)魯棒控制器，基于李雅普諾夫理論分析了該控制系統(tǒng)的穩(wěn)定性，并通過實(shí)驗(yàn)驗(yàn)證了該控制器的實(shí)用性和可行性。方思雨[25]提出了一種基于狀態(tài)量估計(jì)器的準(zhǔn)無(wú)限時(shí)域模型預(yù)測(cè)控制(QHMPC)，采用狀態(tài)量估計(jì)器有效解決了QHMPC算法中一些狀態(tài)量不易觀測(cè)的問題，并針對(duì)節(jié)氣門控制設(shè)計(jì)了相應(yīng)控制器。Gruber等[26]針對(duì)過氧比的控制提出了一種線性模型預(yù)測(cè)控制算法，所提出的線性MPC采用參數(shù)自適應(yīng)的方法來適應(yīng)電堆電流的變化。綜上所述，目前針對(duì)PEMFC陰極供氣系統(tǒng)的研究主要集中在對(duì)過氧比的控制，對(duì)陰極壓力控制的研究較少。然而在無(wú)人機(jī)飛行過程中，高度的變化會(huì)直接引起陰極氣壓的波動(dòng)，進(jìn)而對(duì)燃料電池輸出性能及功率產(chǎn)生較大影響。因此，除了對(duì)過氧比的控制，陰極壓力的控制也是保證無(wú)人機(jī)用PEMFC系統(tǒng)高效運(yùn)行的關(guān)鍵因素[27-28]。

本文首先根據(jù)離心空壓機(jī)內(nèi)氣體流動(dòng)特性，通過預(yù)測(cè)的總熵增和損失建立了不同高度下的空壓機(jī)MAP圖。其次，基于無(wú)刷直流電機(jī)反電勢(shì)特征構(gòu)建了高速空壓機(jī)驅(qū)動(dòng)電機(jī)模型，并將空壓機(jī)模型與驅(qū)動(dòng)電機(jī)模型結(jié)合至陰極空氣供應(yīng)系統(tǒng)模型中。最后，所提出的陰極供氣系統(tǒng)FFM控制可實(shí)現(xiàn)PEMFC在0～3 km寬工況條件下運(yùn)行，滿足不同飛行狀態(tài)下的功率需求，保證在無(wú)人機(jī)飛行狀態(tài)和高度發(fā)生改變時(shí)，PEMFC過氧比和陰極壓力能夠在短時(shí)間內(nèi)跟蹤上給定值，減小由氣壓變化以及供氣不足等對(duì)燃料電池壽命和耐久性的影響。

1 無(wú)人機(jī)用PEMFC陰極供氣系統(tǒng)建模

針對(duì)無(wú)人機(jī)飛行高度的變化，建立了高速離心空壓機(jī)的數(shù)學(xué)模型，并給出了不同高度下的空壓機(jī)特性分析，根據(jù)能量守恒和質(zhì)量連續(xù)方程，對(duì)供應(yīng)歧管、燃料電池電堆和返回歧管進(jìn)行了動(dòng)態(tài)建模，具體PEMFC供氣系統(tǒng)框圖如圖1所示。圖中：Wcp為空壓機(jī)流量；Wsm.out為供應(yīng)歧管出口流量；Wca.out為陰極出口流量；Wrm.out為返回歧管出口流量;Wan.in和Wan.out分別為陽(yáng)極入口和出口流量。

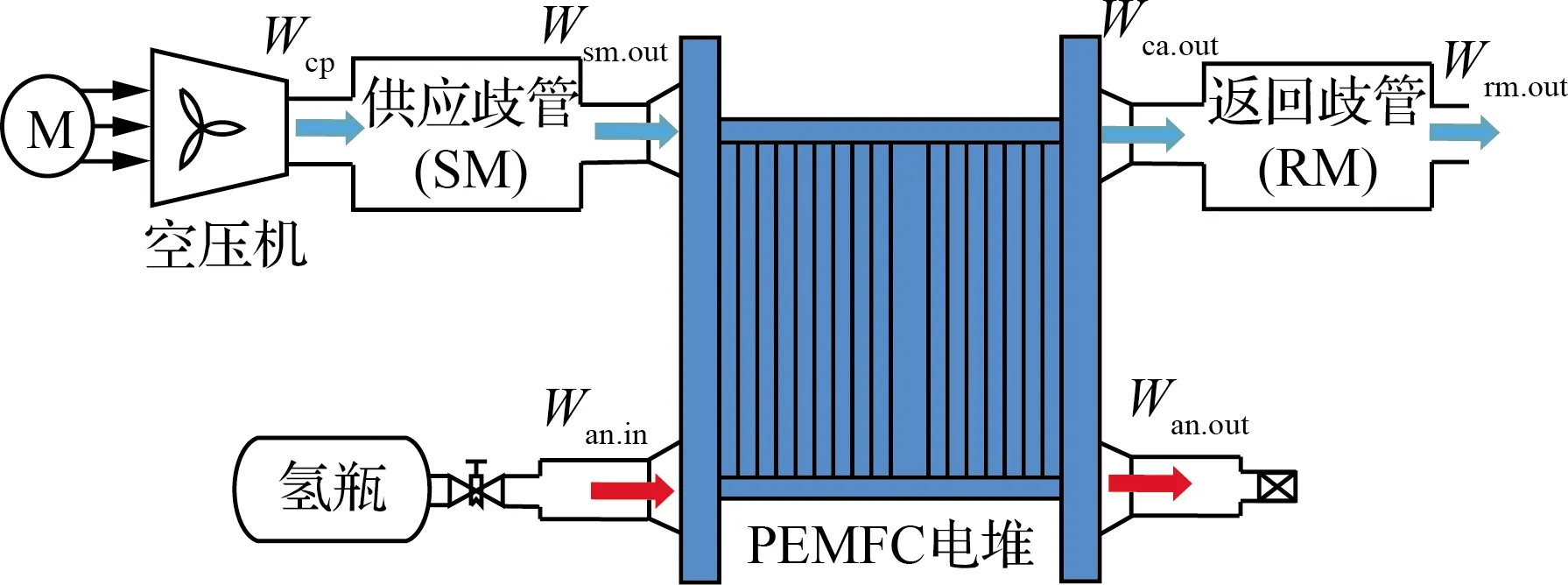
圖1 PEMFC系統(tǒng)框圖

1.1 變高度下空壓機(jī)與驅(qū)動(dòng)電機(jī)建模

目前針對(duì)PEMFC陰極供氣系統(tǒng)中采用的空壓機(jī)模型，主要是通過神經(jīng)網(wǎng)絡(luò)等數(shù)據(jù)擬合方法得到，其建模過程存在數(shù)據(jù)量大、處理難度高等缺點(diǎn)，建立的空壓機(jī)模型大多只適用于地面，未考慮環(huán)境變化對(duì)其帶來的影響。因此，建立變高度下空壓機(jī)及驅(qū)動(dòng)電機(jī)模型并進(jìn)行控制，對(duì)燃料電池系統(tǒng)在中低空環(huán)境下的實(shí)際應(yīng)用具有重要意義。

1.1.1 環(huán)境模型

空壓機(jī)入口氣體特性隨著高度的變化而改變，而入口氣體的溫度Th、壓力Ph、空氣密度ρh等均會(huì)直接影響到空壓機(jī)出口氣壓Pcp的大小。因此，研究不同高度下的氣體特性對(duì)變高度下的空壓機(jī)建模十分重要。在海拔高度小于11 km時(shí)，Th及Ph與海拔高度h有如下關(guān)系[29]:

Th=T0+Lt(h-h0)

(1)

(2)

式中：T0=293 K;P0=101 325 Pa;h0=0 m;R為理想氣體常數(shù)；g0為重力加速度常數(shù)；Ma為空氣的摩爾質(zhì)量；Lt為溫度變化率。

空壓機(jī)入口空氣密度的大小直接影響到空壓機(jī)的能量轉(zhuǎn)換效率。水平面處的空氣密度約為1.29 kg/m3，海拔高度h處的空氣密度ρh可表示為

(3)

式中：Z為壓縮系數(shù)。

1.1.2 變高度下空壓機(jī)特性

與容積式空壓機(jī)不同，離心空壓機(jī)的輸出流量與壓力間存在強(qiáng)耦合關(guān)系。假設(shè)氣體壓縮為等熵壓縮，考慮能量傳遞對(duì)空壓機(jī)性能的影響，變高度下空壓機(jī)的工作特性可表示為

Δht(ωcp,Wcp)=Δhs(ωcp,Wcp)+Δhi(ωcp,Wcp)+

Δhf(ωcp,Wcp)+Δhother(ωcp,Wcp)

(4)

(5)

(6)

式中：Δht為焓的總增加量；Δhs為實(shí)際焓增量；Δhi、Δhf分別為氣體在葉片入口處和擴(kuò)散器處因入射損失、摩擦損失引起的熵增；Δhother為在壓縮過程中由其他損失引起的熵增，這里假設(shè)為總熵增的8%;ωcp為轉(zhuǎn)軸的旋轉(zhuǎn)速度；Pcp、Tcp.out分別為空壓機(jī)出口的氣體壓力和溫度；ψ為空氣機(jī)壓比；cp為定壓比熱容；cv為定容比熱容；γ=cp/cv為比熱容比,約為1.4。

式(4)中空壓機(jī)出口流量Wcp可根據(jù)供應(yīng)歧管氣壓Psm與空壓機(jī)壓比ψ得到：

(7)

式中：A1為空壓機(jī)葉輪眼面積;Lc為空壓機(jī)氣體傳輸管道長(zhǎng)度。

滯止焓的表達(dá)式為

(8)

(9)

壓縮過程中的摩擦損失與雷諾數(shù)Re相關(guān)，不同條件下雷諾數(shù)的變化對(duì)空壓機(jī)的輸出性能會(huì)產(chǎn)生較大影響。在變高度條件下，摩擦損失Δhf與Re的關(guān)系如式(10)～式(12)所示：

Δhf=Δhfi+Δhfd

(10)

(11)

(12)

式中：Δhfi和Δhfd分別為在葉輪和擴(kuò)散器處的摩擦損失；li和ld分別為平均葉輪管道長(zhǎng)度、平均擴(kuò)散器管道長(zhǎng)度；Di和Dd分別為葉輪處平均液壓管道直徑、擴(kuò)散器處的平均液壓管道直徑；α2b為相對(duì)于切線方向的擴(kuò)壓器進(jìn)口角；A1為流通面積；f為平均雷諾數(shù)的摩擦系數(shù),

f=0.316 4(Re)-0.25

(13)

(14)

其中：D2為葉輪尖端直徑；u2為葉輪葉片出口的圓周速度；μ2為葉輪出口氣體溫度為T2時(shí)的動(dòng)力黏度，假設(shè)為常數(shù)20.5×10-6kg·s/m2;ρ2為葉輪出口氣體密度。

基于式(1)～式(14)，給出了空壓機(jī)在0、2、3 km處的MAP圖，分別反映了在相應(yīng)高度下空壓機(jī)轉(zhuǎn)速、質(zhì)量流量以及出口氣壓間的動(dòng)態(tài)關(guān)系，如圖2所示。其中，通過實(shí)驗(yàn)測(cè)量獲得的空壓機(jī)地面數(shù)據(jù)在圖2(a)中給出。

由圖2可看出，所建立的空壓機(jī)特性模型與實(shí)驗(yàn)測(cè)量數(shù)據(jù)有較好的吻合度，且隨著高度的增加，空壓機(jī)輸出氣體的質(zhì)量流量及壓力范圍逐漸變窄，空壓機(jī)正常工作范圍縮小。在海拔0、2、3 km 高度下，最大輸出質(zhì)量流量分別為0.024 2、0.019 5、0.017 5 kg/s，相應(yīng)的最大輸出壓力分別為1.732×105、1.391×105、1.251×105Pa。

圖2 不同高度下空壓機(jī)MAP圖

1.1.3 空壓機(jī)驅(qū)動(dòng)電機(jī)建模

空壓機(jī)由每一時(shí)刻兩兩導(dǎo)通，三相六狀態(tài)運(yùn)行的無(wú)刷直流電機(jī)(BLDCM)驅(qū)動(dòng)，如圖3所示。

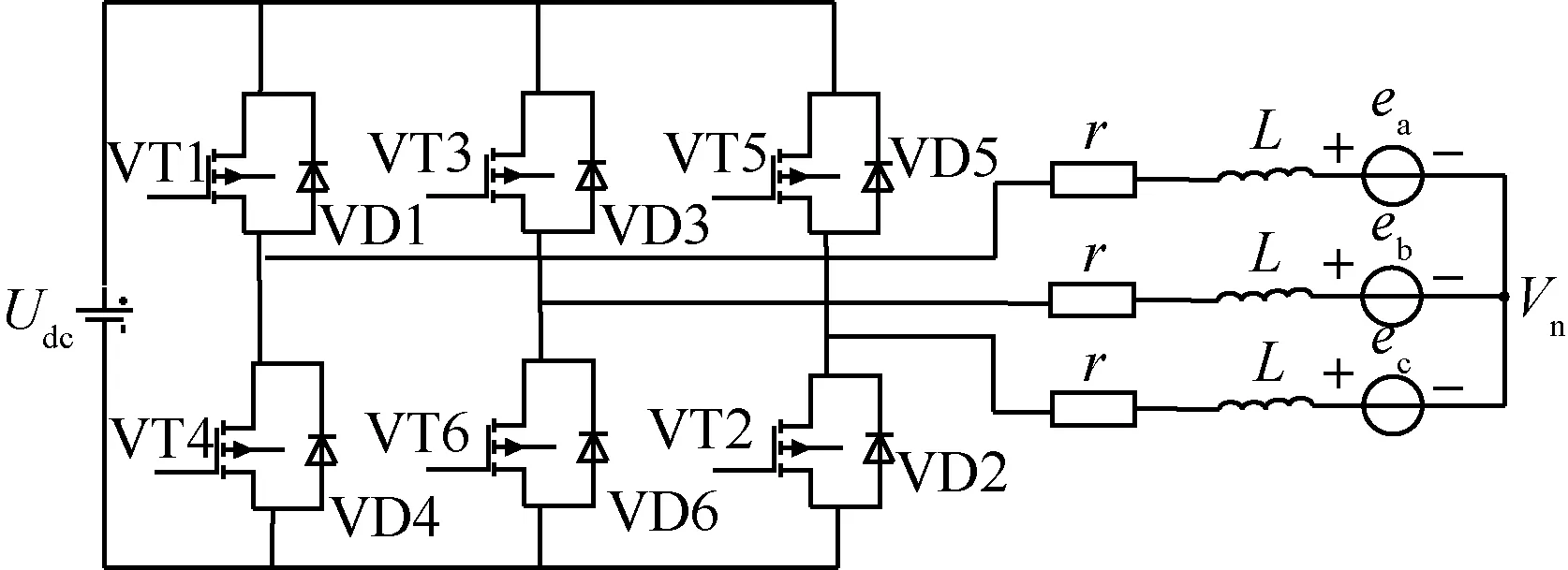
圖3 無(wú)刷直流電機(jī)原理圖

BLDCM三相電壓平衡方程為

(15)

式中：ua、ub、uc和ia、ib、ic以及ea、eb、ec分別是相電壓、相電流和各相的反電動(dòng)勢(shì)；r=ra=rb=rc為定子電阻；L為定子電感；Vn為電機(jī)三相繞組中性點(diǎn)的電壓。采用星型連接，三相反電勢(shì)和三相電流間存在以下關(guān)系：

|ea|=|eb|=|ec|=Cφωcp

(16)

ia+ib+ic=0

(17)

式中：Cφ為磁鏈。

BLDCM三相理想反電動(dòng)勢(shì)對(duì)應(yīng)的電流波形、霍爾信號(hào)如圖4所示。

圖4 理想反電動(dòng)勢(shì)、電流及霍爾信號(hào)

BLDCM的動(dòng)態(tài)特性方程為

(18)

(19)

(20)

式中：J為轉(zhuǎn)動(dòng)慣量；τcm為無(wú)刷直流電機(jī)產(chǎn)生的電磁轉(zhuǎn)矩；τcp為空壓機(jī)的負(fù)載轉(zhuǎn)矩；ηcp為空壓機(jī)的效率。

1.2 歧管動(dòng)態(tài)建模

1.2.1 供應(yīng)歧管建模

供應(yīng)歧管入口流量為空壓機(jī)的輸出流量Wcp，供應(yīng)歧管出口流量為Wsm.out，根據(jù)能量守恒和質(zhì)量連續(xù)方程，供應(yīng)歧管的壓力表達(dá)式為[30]

(21)

式中：Ra為空氣氣體常數(shù)；Tcp.out為空壓機(jī)出口氣體溫度；Vsm為供應(yīng)歧管體積；Tcp.out與空壓機(jī)壓比和效率有關(guān)，即

(22)

式中：ηcp為空壓機(jī)效率。

Wsm.out與Psm和陰極壓力Pca有關(guān)，即

Wsm.out=Ksm.out(Psm-Pca)

(23)

1.2.2 返回歧管建模

返回歧管的壓力與陰極出口流量Wca.out和返回歧管出口流量Wrm.out相關(guān)，表達(dá)式為

(24)

陰極出口流量的表達(dá)式為

Wca.out=Kca.out(Pca-Prm)

(25)

式中：Trm為返回歧管氣體的溫度，假設(shè)與燃料電池電堆溫度Tst相同；Vrm為返回歧管體積；Kca.out為返回歧管的流量系數(shù)。

返回歧管出口流量Wrm.out是關(guān)于返回歧管壓力Prm和末端環(huán)境氣壓Ph的函數(shù)：

(26)

式中：ADrm為返回歧管閥門的開口面積。

1.3 燃料電池電堆建模

1.3.1 陰極氣壓建模

陰極氣壓建模描述的是陰極內(nèi)部氣體的動(dòng)態(tài)變化特性，其中，氧氣和氮?dú)馐顷帢O流道中主要?dú)怏w成分，氧氣和氮?dú)夥謮嚎筛鶕?jù)氣體的質(zhì)量守恒和理想氣體定律得到[31]:

(27)

(28)

Pca=PO2+PN2+Psat

(29)

式中：Vca為陰極體積；MO2和MN2分別為氧氣和氮?dú)獾哪栙|(zhì)量；WO2.in和WN2.in分別為陰極入口處氧氣和氮?dú)獾馁|(zhì)量流量；WO2.out和WN2.out分別為陰極出口處氧氣和氮?dú)獾馁|(zhì)量流量；WO2.react為陰極消耗氧氣的質(zhì)量流量；Psat為飽和水蒸汽壓力。

1.3.2 燃料電池電堆電壓建模

燃料電池電堆模型由N片燃料電池單體串聯(lián)組成，電堆輸出電壓為[32-34]

Vst=NVfc=N(Enernst-Vact-Vohm-Vcon)

(30)

式中：Vfc為燃料電池單體輸出電壓；Enernst為能斯特電動(dòng)勢(shì)；Vact為活化損失過電勢(shì)；Vohm為歐姆損失過電勢(shì)；Vcon為濃差損失過電勢(shì)。能斯特電動(dòng)勢(shì)以及3種損失過電勢(shì)的表達(dá)式為

Enernst=1.229-8.5×10-4×(Tfc-298.15)+

(31)

Vact=V0+Va(1-e-c1j)

(32)

(33)

Vohm=j·Rohm

(34)

式中：Tfc為燃料電池工作溫度，假設(shè)與燃料電池電堆溫度Tst相同；V0為電流密度為零時(shí)的壓降；Va與溫度和氧氣分壓有關(guān)；Rohm為歐姆內(nèi)阻；j和jmax分別為電流密度和最大電流密度；c1、c3均為常數(shù)；c2與飽和水蒸氣壓力和燃料電池工作溫度有關(guān)，電堆各參數(shù)的取值及表達(dá)式見附錄A。

2 控制器設(shè)計(jì)

PEMFC系統(tǒng)是一個(gè)具有非線性、強(qiáng)耦合性的多輸入多輸出系統(tǒng)，其系統(tǒng)效率和動(dòng)態(tài)性能受到陰極供氣系統(tǒng)的直接影響。本文的控制目標(biāo)為基于所建PEMFC陰極供氣系統(tǒng)模型，避免氧饑餓，并保持PEMFC系統(tǒng)的高工作效率。為使控制效果最優(yōu)，本文提出了針對(duì)過氧比和陰極壓力的雙閉環(huán)控制，控制系統(tǒng)結(jié)構(gòu)如圖5所示。

如圖5所示，陰極壓力基于分?jǐn)?shù)階PIλDμ控制，通過調(diào)節(jié)返回歧管閥門開口面積來控制陰極壓力保持在給定值，過氧比控制由分?jǐn)?shù)階PIλDμ控制外環(huán)和MPC控制內(nèi)環(huán)組成，該控制策略簡(jiǎn)寫為FFM。首字母F代表陰極壓力分?jǐn)?shù)階控制，后者F代表過氧比分?jǐn)?shù)階控制，M代表電機(jī)轉(zhuǎn)矩模型預(yù)測(cè)控制，并在圖5中分別給出了模型和控制模塊所對(duì)應(yīng)的公式。

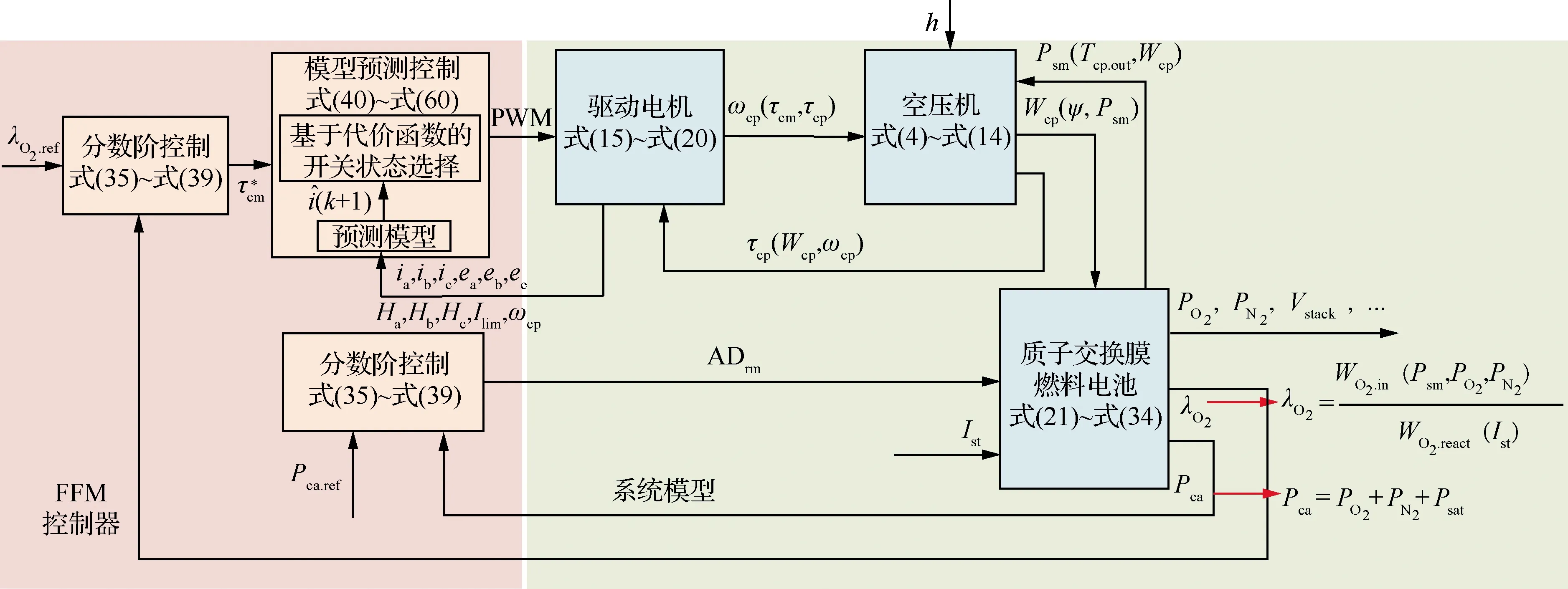
圖5 FFM 控制系統(tǒng)框圖

2.1 陰極壓力與過氧比控制器設(shè)計(jì)

2.1.1 分?jǐn)?shù)階PIλDμ控制器

以陰極壓力分?jǐn)?shù)階PIλDμ控制器為例，結(jié)構(gòu)框圖如圖6所示。圖中，分?jǐn)?shù)階PIλDμ控制器的時(shí)域表達(dá)式為

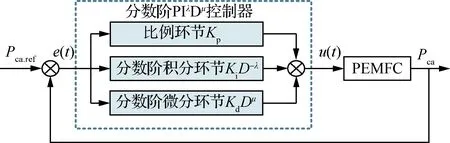
圖6 陰極壓力控制結(jié)構(gòu)

u(t)=Kpe(t)+KiD-λe(t)+KdDμe(t)

(35)

式中：u(t)為返回歧管閥門開口面積；e(t)為陰極壓力參考值與系統(tǒng)輸出的差值ΔPca。

2.1.2 分?jǐn)?shù)階PIλDμ控制器設(shè)計(jì)

設(shè)計(jì)一個(gè)分?jǐn)?shù)階PIλDμ控制器需要確定5個(gè)參數(shù)：Kp、Ki、Kd、λ和μ。為使所設(shè)計(jì)的分?jǐn)?shù)階PIλDμ控制器控制效果最優(yōu)，在傳統(tǒng)參數(shù)整定方法——主導(dǎo)極值點(diǎn)法的基礎(chǔ)上，采用了一種新的參數(shù)整定方法——極點(diǎn)階數(shù)搜索法。并以陰極壓力控制為例，給出了基于極點(diǎn)階數(shù)搜索法的分?jǐn)?shù)階PIλDμ控制器設(shè)計(jì)的具體步驟，并以時(shí)間乘絕對(duì)誤差積分準(zhǔn)則(ITAE)作為控制參數(shù)整定的性能指標(biāo)。

步驟1估計(jì)比例增益Kp。

Kp的估計(jì)值可根據(jù)系統(tǒng)穩(wěn)態(tài)誤差ΔPca與理想給定值Pca.ref之比Et得到：

Kp=[100/(Et0Pca.ref)-1]a0

(36)

式中：a0為被控系統(tǒng)傳遞函數(shù)中的系數(shù)，防止Kp過大導(dǎo)致系統(tǒng)不穩(wěn)定。Et0和Et存在以下關(guān)系：

(37)

步驟2確定極點(diǎn)S1,2。

系統(tǒng)極點(diǎn)主要對(duì)系統(tǒng)的閉環(huán)響應(yīng)過程產(chǎn)生影響，當(dāng)閉環(huán)系統(tǒng)主要受到一對(duì)主導(dǎo)極點(diǎn)的影響時(shí)，該對(duì)主導(dǎo)極點(diǎn)用以下形式給出[35]

(38)

式中：σ為極點(diǎn)穩(wěn)定度;ξ為阻尼比。

當(dāng)步驟1和步驟2中的Kp和S1,2確定后，采用階數(shù)搜索方法來確定控制器中其余的4個(gè)參數(shù):Ki、Kd、λ和μ。

步驟3確定積分階次λ和微分階次μ的第i(1≤i≤3)次搜索范圍。

當(dāng)i=1時(shí)，μ∈[0,2.0],λ∈[0,1.5]，搜索步長(zhǎng)Δ1=0.1。

當(dāng)i>1時(shí)，μ∈[max(Δi,μi-1-2Δi-1),μi-1+2Δi-1],λ∈[max(Δi,λi-1-2Δi-1),λi-1+2Δi-1]，搜索步長(zhǎng)Δi=Δi-1/10。

步驟4確定i次搜索時(shí)的Kd、μ、Ki、λ。

將步驟1～步驟4中得到的Kp、S1,2和λ、μ的第i次搜索范圍中的值依次代入特征方程中，并令其等于零，即可解得每組的控制參數(shù)Kd、μ,Ki、λ。根據(jù)系統(tǒng)性能指標(biāo)(ITAE)來判定所得參數(shù)是否滿足要求，若有一組參數(shù)滿足指標(biāo)要求，則結(jié)束搜索；若均不滿足指標(biāo)要求，則記錄第i次搜索中最接近指標(biāo)要求的μi和λi，使i=i+1，若i≤3則返回步驟3，若i>3則進(jìn)行步驟5。

步驟5重新搜索5個(gè)參數(shù)。

若系統(tǒng)階躍響應(yīng)時(shí)的ITAE較大或調(diào)節(jié)時(shí)間T較長(zhǎng)，則適當(dāng)增大Kp，若系統(tǒng)階躍響應(yīng)的超調(diào)較大，則適當(dāng)減小Kp，并重復(fù)執(zhí)行步驟2～步驟4。具體的分?jǐn)?shù)階PIλDμ控制器設(shè)計(jì)流程如圖7所示。

圖7 最優(yōu)分?jǐn)?shù)階PIλDμ控制設(shè)計(jì)流程

文中選用ITAE優(yōu)化準(zhǔn)則的數(shù)學(xué)定義為

(39)

式中：r(t)為閉環(huán)系統(tǒng)給定參考值；y(t)為閉環(huán)系統(tǒng)實(shí)際輸出值。

2.2 電機(jī)驅(qū)動(dòng)轉(zhuǎn)矩控制器設(shè)計(jì)

2.2.1 電流預(yù)測(cè)模型建立

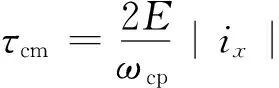
當(dāng)無(wú)刷直流處于換相時(shí)刻時(shí)，a、b、c相電壓與直流母線電壓的關(guān)系為

(40)

δ值與非換相相、續(xù)流電流大小以及導(dǎo)通相開關(guān)管開通關(guān)斷有關(guān)，假設(shè)δx、δy、δz分別對(duì)應(yīng)非換相相、續(xù)流電流相和導(dǎo)通相。在電機(jī)運(yùn)行6狀態(tài)下，非換相相δx、續(xù)流電流相δy和導(dǎo)通相δz因運(yùn)行狀態(tài)的不同，均可表示電機(jī)a、b、c三相中的任意一相。

因此，狀態(tài)變量為相電流ia、ib、ic以及轉(zhuǎn)速ωcp，控制變量為開關(guān)狀態(tài)δa、δb、δc以及轉(zhuǎn)矩τcm。

上管調(diào)制：當(dāng)由c+b-轉(zhuǎn)換為a+b-拍時(shí)(即VT5、VT6導(dǎo)通→VT1、VT6導(dǎo)通)，

ea=-eb=E

(41)

1)ic≠0A(即c相電流續(xù)流)，若VT1導(dǎo)通，則δz=δa=1、δx=δb=0、δy=δc=0。若VT1關(guān)斷，則δz=δa=0、δx=δb=0、δy=δc=0。使用基爾霍夫定律得到當(dāng)VT1處于導(dǎo)通和關(guān)斷狀態(tài)時(shí)a、b、c相電壓方程為

VT1導(dǎo)通時(shí):

(42)

VT1關(guān)斷時(shí):

(43)

將式(15)、式(40)～式(43)離散化得到

(44)

(45)

式中：ib(k+1)、ib(k)分別為非換相相k+1時(shí)刻和k時(shí)刻電流值；Ts為采樣周期；on和off分別表示換相開關(guān)管開通及關(guān)斷狀態(tài)。

2)ic=0 A(即c相電流續(xù)流結(jié)束)，若VT1導(dǎo)通，則δz=δa=1、δx=δb=0、δy=δc=0。若VT1關(guān)斷，則δz=δa=0、δx=δb=0、δy=δc=0。使用基爾霍夫定律得到當(dāng)VT1處于導(dǎo)通和關(guān)斷狀態(tài)時(shí)a、b相電壓方程為

VT1導(dǎo)通時(shí):

(46)

VT1關(guān)斷時(shí):

(47)

將式(15)、式(41)、式(46)、式(47)離散化后得到

(48)

(49)

下管調(diào)制：當(dāng)由a+b-轉(zhuǎn)換為a+c-拍時(shí)(即VT1、VT6導(dǎo)通→VT1、VT2導(dǎo)通)，

ea=-ec=E

(50)

1)ib≠0A(即b相電流續(xù)流)，若VT2導(dǎo)通，則δx=δa=1、δy=δb=1、δz=δc=0。若VT2關(guān)斷，則δx=δa=1、δy=δb=1、δz=δc=1。使用基爾霍夫定律分別得到當(dāng)VT2處于導(dǎo)通和關(guān)斷狀態(tài)時(shí)a、b、c相電壓方程為

VT2導(dǎo)通時(shí):

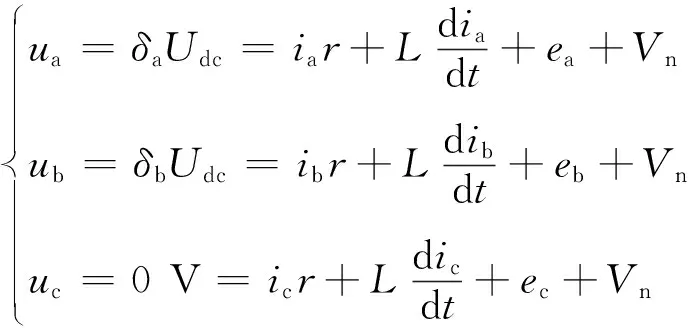
(51)

VT2關(guān)斷時(shí):

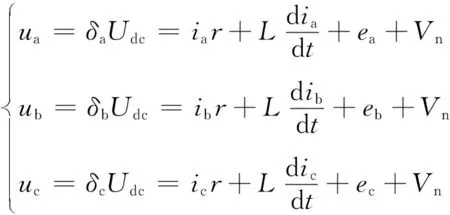
(52)

將式(15)、式(40)、式(50)～式(52)離散化得到

(53)

(54)

2)ib=0A(即b相電流續(xù)流結(jié)束)，若VT2導(dǎo)通，則δx=δa=1、δy=δb=0、δz=δc=0。若VT2關(guān)斷，則δx=δa=1、δy=δb=0、δz=δc=1。使用基爾霍夫定律得到當(dāng)VT2處于導(dǎo)通和關(guān)斷狀態(tài)時(shí)a、c相電壓方程為

VT2導(dǎo)通時(shí):

(55)

VT2關(guān)斷時(shí):

(56)

將式(15)、式(50)、式(55)、式(56)離散化后得到：

(57)

(58)

基于包含逆變器數(shù)學(xué)模型的預(yù)測(cè)模型，有限集模型預(yù)測(cè)控制分別考慮了在導(dǎo)通相電流續(xù)流(iy≠0 A)和續(xù)流結(jié)束(iy=0 A)兩種情況下，導(dǎo)通相功率開關(guān)管分別開通或者關(guān)斷狀態(tài)時(shí)，電機(jī)非換相相未來時(shí)刻電流有4種可能預(yù)測(cè)值。同時(shí)，當(dāng)電機(jī)在ab、ac、bc、ba、ca、cb相導(dǎo)通的6種不同運(yùn)行條件下，下一時(shí)刻預(yù)測(cè)值也是不同的，故每個(gè)周期共有24種有限情況。

2.2.2 滾動(dòng)優(yōu)化

根據(jù)2.2.1節(jié)建立的電流預(yù)測(cè)模型，為減小非換相相電流波動(dòng)，最小化非換相相電流以及對(duì)電流幅值進(jìn)行約束，設(shè)計(jì)代價(jià)函數(shù)：

(59)

(60)

取min={J1,J2}，決定下一時(shí)刻導(dǎo)通相開關(guān)管的on或off狀態(tài)。

因無(wú)刷直流電機(jī)的極對(duì)數(shù)p=1，運(yùn)行頻率為0～4 667 Hz。為保證模型與控制策略的可靠性，仿真速度應(yīng)大于50倍電機(jī)頻率，故文中設(shè)置模型預(yù)測(cè)的采樣頻率為250 kHz，步長(zhǎng)Ts=4×10-6。文中采用的模型預(yù)測(cè)為一步預(yù)測(cè)，即預(yù)測(cè)時(shí)域?yàn)?。

圖8 模型預(yù)測(cè)控制系統(tǒng)框圖

3 仿真結(jié)果分析

為驗(yàn)證建立的系統(tǒng)模型和提出的FFM控制方法，基于無(wú)人機(jī)飛行任務(wù)模擬過程，對(duì)控制的快速動(dòng)態(tài)響應(yīng)特性和抑制轉(zhuǎn)矩脈動(dòng)特性在MATLAB/Simulink上進(jìn)行了仿真分析。同時(shí)，與PPM控制(首字母P代表陰極壓力PID控制、后者P代表過氧比PID控制、M代表電機(jī)轉(zhuǎn)矩MPC控制)和PPP控制(首字母P代表陰極壓力PID控制、中間P代表過氧比PID控制、后者P代表電機(jī)轉(zhuǎn)矩PID控制)進(jìn)行了對(duì)比。燃料電池、空壓機(jī)及驅(qū)動(dòng)電機(jī)和3種控制方法的詳細(xì)參數(shù)請(qǐng)見附錄A。

無(wú)人機(jī)飛行任務(wù)模擬過程如圖9所示。其中，陰極壓力與過氧比給定值的設(shè)置依據(jù)與不同高度下空壓機(jī)的工作特性有關(guān)，在20 s后，巡航負(fù)載電流小，空壓機(jī)輸入流量低，導(dǎo)致空壓機(jī)實(shí)際工作點(diǎn)在喘振線左側(cè)，為保證空壓機(jī)始終工作在正常工作區(qū)域，將過氧比參考值提高至5，同時(shí)將陰極壓力參考值降至地面氣壓1 atm(1 atm=101 325 Pa)。

圖9 無(wú)人機(jī)飛行任務(wù)模擬

3.1 陰極壓力閉環(huán)控制

3種控制下陰極壓力的控制效果如圖10所示，由圖可見，3種控制方法均可實(shí)現(xiàn)將陰極壓力控制在參考值附近，且穩(wěn)態(tài)誤差較小可忽略。在20 s參考值發(fā)生改變時(shí)，F(xiàn)FM調(diào)節(jié)時(shí)間相比PPM減小了0.5 s,僅為PPM調(diào)節(jié)時(shí)間的37%，PPM和PPP兩種控制下的陰極氣壓無(wú)明顯差異；在30 s和34 s時(shí)，因受空壓機(jī)流量控制的耦合影響，陰極氣壓分別有一個(gè)短暫減小和短暫增大的過程，但陰極氣壓減小和增大的幅度及響應(yīng)時(shí)間都較小，可忽略，因此圖中未給出這兩個(gè)時(shí)間的局部放大圖。

圖10 陰極氣壓控制效果

調(diào)節(jié)返回氣管閥門開口面積的大小是實(shí)現(xiàn)陰極氣壓控制的有效途徑之一，閥門開口面積越大，陰極氣壓越低。在20 s時(shí)，因陰極氣壓參考值減小，導(dǎo)致閥門開口面積突然增加，以期在短時(shí)間內(nèi)降低陰極氣壓跟蹤上給定值，閥門開口面積的變化情況如圖11所示。

3.2 過氧比閉環(huán)控制

3種控制方法下過氧比的控制效果如圖12所示。其中圖12(a)是過氧比的整體控制效果，可見在無(wú)人機(jī)飛行狀態(tài)發(fā)生改變時(shí)，3種控制方法均可將過氧比穩(wěn)定在給定值附近，F(xiàn)FM相比PPM和PPP，在調(diào)節(jié)時(shí)間上具有明顯的優(yōu)勢(shì)，而3種控制方法的超調(diào)量和穩(wěn)態(tài)誤差均差異不大。

圖12(b)為無(wú)人機(jī)飛行狀態(tài)由爬升到3 km 巡航時(shí)的局部放大圖，此時(shí)無(wú)人機(jī)需求功率急劇減小，且因3 km處空壓機(jī)特性的限制，需對(duì)過氧比做出相應(yīng)的改變。由圖可見，F(xiàn)FM控制的過氧比可以在較短的時(shí)間內(nèi)跟蹤上給定值，且相比PPM和PPP分別減少了75%和80%的調(diào)節(jié)時(shí)間，具體調(diào)節(jié)時(shí)間如表1所示。

圖12(c)為無(wú)人機(jī)飛行狀態(tài)由3 km巡航到下降時(shí)的局部放大圖，此時(shí)無(wú)人機(jī)需求功率繼續(xù)減小。由表1可知，F(xiàn)FM在調(diào)節(jié)時(shí)間上同樣具有最優(yōu)的控制效果，相比于PPM，其調(diào)節(jié)時(shí)間減小了60%，PPM和PPP的控制效果無(wú)明顯差異。

圖12(d)為無(wú)人機(jī)飛行狀態(tài)由下降到2 km 巡航時(shí)的局部放大圖，此時(shí)無(wú)人機(jī)需求功率增加，3種控制策略的調(diào)節(jié)時(shí)間如表1所示，F(xiàn)FM控制的調(diào)節(jié)時(shí)間僅為PPM控制的28%，為PPP控制的50%。

表1 3種控制方法過氧比控制的調(diào)節(jié)時(shí)間

過氧比定義為進(jìn)入陰極的氧氣流量與反應(yīng)消耗氧氣流量的比值，因此，過氧比的控制與空壓機(jī)的流量緊密相關(guān)，圖13給出了空壓機(jī)流量的控制效果。

圖13 空壓機(jī)流量控制效果

電機(jī)驅(qū)動(dòng)轉(zhuǎn)矩的脈動(dòng)會(huì)導(dǎo)致其運(yùn)行轉(zhuǎn)速的不穩(wěn)定，嚴(yán)重時(shí)更會(huì)造成電機(jī)的損壞。本文為減小轉(zhuǎn)矩脈動(dòng)對(duì)電機(jī)的損害，提出了對(duì)轉(zhuǎn)矩的MPC控制。基于FFM、PPM和PPP這3種控制下的電機(jī)驅(qū)動(dòng)轉(zhuǎn)矩如圖14所示，由圖可見，F(xiàn)FM和PPM控制下的電機(jī)轉(zhuǎn)矩特性無(wú)明顯區(qū)別，但相比PPP，轉(zhuǎn)矩脈動(dòng)減小了接近50%，有效降低了轉(zhuǎn)矩脈動(dòng)對(duì)驅(qū)動(dòng)電機(jī)帶來的損害。

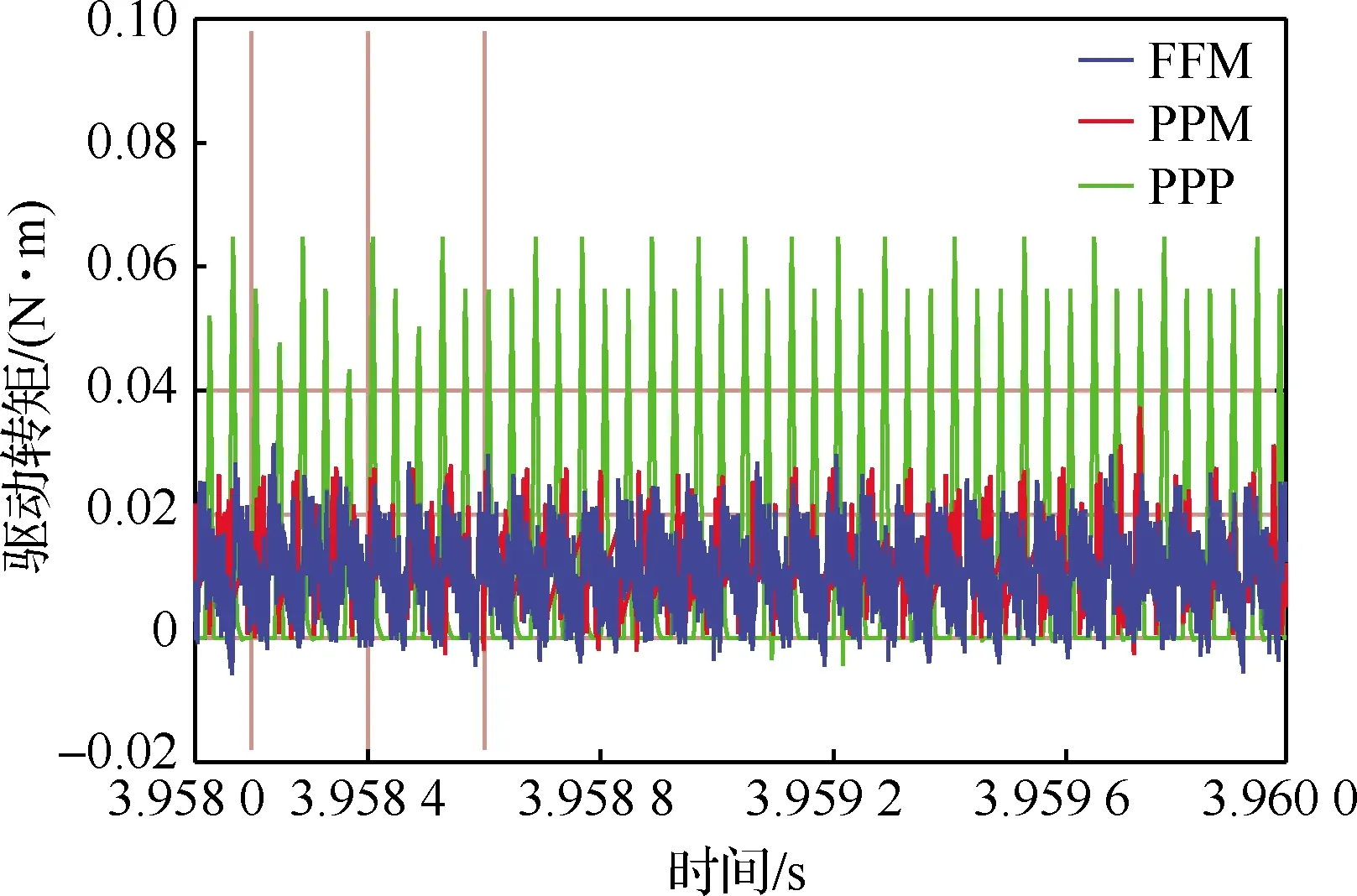
圖14 驅(qū)動(dòng)轉(zhuǎn)矩控制

圖15為FFM、PPP和PPM控制下的a相電壓電流，對(duì)比可知，F(xiàn)FM和PPM控制下的a相電流脈動(dòng)，僅為PPP控制的50%左右。因此，通過對(duì)圖14和圖15的對(duì)比分析可知，所提出的電機(jī)轉(zhuǎn)矩MPC控制算法可有效降低轉(zhuǎn)矩的脈動(dòng)。

圖15 3種控制方法下的a相電壓、電流

文中無(wú)人機(jī)動(dòng)力系統(tǒng)包含鋰電池和PEMFC兩種能源裝置，鋰電池僅用于啟動(dòng)時(shí)空壓機(jī)的供電，PEMFC作為能源裝置為不同飛行狀態(tài)下的無(wú)人機(jī)提供需求功率，PEMFC系統(tǒng)輸出功率的大小與無(wú)人機(jī)飛行狀態(tài)緊密相關(guān)。圖16和圖17分別給出了3種控制策略下電堆電壓和功率的控制效果，由圖可見，無(wú)人機(jī)起飛及爬升階段、巡航階段和下降階段電堆輸出功率分別為9.4、4.4、3.5 kW，電堆電壓相應(yīng)為52、67、72 V，可滿足圖9中無(wú)人機(jī)在起飛和爬升階段的大功率需求。

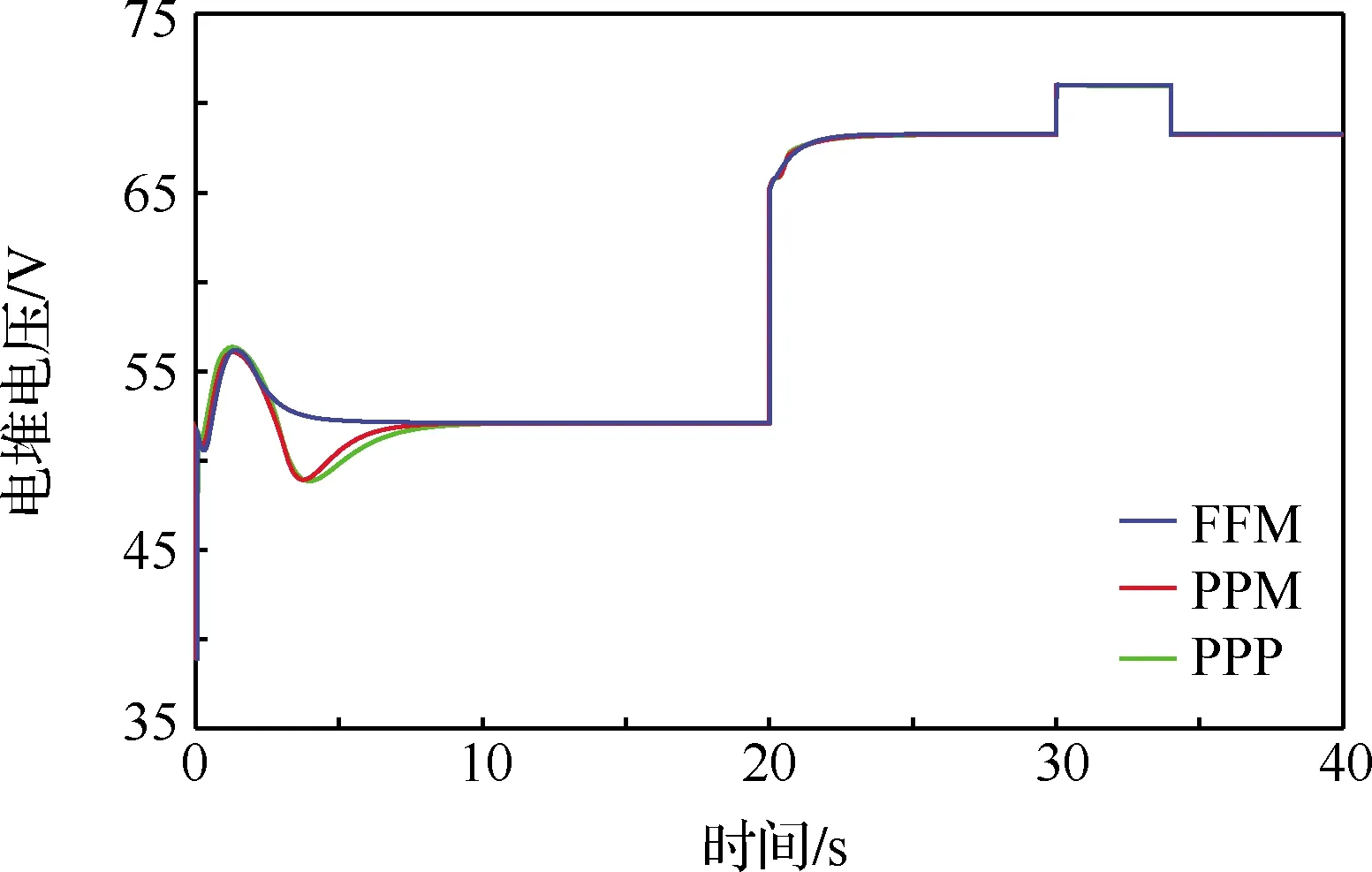
圖16 電堆輸出電壓

圖17 電堆輸出功率控制效果

4 結(jié) 論

1)針對(duì)無(wú)人機(jī)用燃料電池在不同飛行高度下面臨的環(huán)境差異，考慮空壓機(jī)入口處氣體的溫度、壓力、密度以及雷諾數(shù)等影響，構(gòu)建了跨高度離心式空壓機(jī)模型、分析了不同高度下的空壓機(jī)特性MAP圖，在所建空壓機(jī)模型的基礎(chǔ)上完成了跨高度燃料電池陰極供氣系統(tǒng)建模及控制方法的研究。

2)基于無(wú)刷直流反電勢(shì)特征構(gòu)建了高速離心式空壓機(jī)驅(qū)動(dòng)電機(jī)模型，同時(shí)針對(duì)電機(jī)驅(qū)動(dòng)轉(zhuǎn)矩采用了有限集模型預(yù)測(cè)控制，并通過仿真驗(yàn)證了MPC控制方法可有效降低驅(qū)動(dòng)轉(zhuǎn)矩脈動(dòng)。

3)所提出的FFM控制能夠根據(jù)陰極氣壓及過氧比的變化，及時(shí)調(diào)整陰極背壓閥開口面積和電機(jī)驅(qū)動(dòng)轉(zhuǎn)矩，進(jìn)而通過電機(jī)驅(qū)動(dòng)轉(zhuǎn)矩調(diào)節(jié)空壓機(jī)轉(zhuǎn)速，以在短時(shí)間內(nèi)跟蹤上過氧比及陰極壓力參考量，具有可調(diào)參數(shù)范圍大、動(dòng)態(tài)響應(yīng)速度快、電機(jī)轉(zhuǎn)矩脈動(dòng)小等特點(diǎn)。所提出的FFM控制可實(shí)現(xiàn)燃料電池在0～3 km寬工況條件下運(yùn)行，并滿足無(wú)人機(jī)不同飛行狀態(tài)下的功率需求。

附錄A

空壓機(jī)及驅(qū)動(dòng)電機(jī)參數(shù)見表A1。

表A1 空壓機(jī)及驅(qū)動(dòng)電機(jī)參數(shù)

Table A1 Parameters of air compressor and brushless motor

符號(hào)定義單位數(shù)值ψ地面最大壓力比1.7Wcp地面最大流量g/s24ηsmax地面最大等熵效率70m重量g600Pe額定功率W1 000p極對(duì)數(shù)1J轉(zhuǎn)動(dòng)慣量kg·m25.5×10-7C?磁鏈Wb6.6×10-3Ie額定相電流A2.7r定子電阻Ω0.9L定子電感μH160σ滑移因子0.875A1流通面積m27.9×10-5β1b葉片入口角度(°)28β2b轉(zhuǎn)子葉片角度(°)80r1平均誘導(dǎo)半徑m0.010 3

燃料電池參數(shù)見表A2。

表A2 燃料電池參數(shù)

Table A2 Fuel cell parameters

符號(hào)定義單位數(shù)值N單電池個(gè)數(shù)100γ空氣比熱容比1.4Tst電池堆溫度K313.15Tatm環(huán)境溫度K298.15Vsm供應(yīng)岐管體積m30.01Vca陰極體積m30.01Vrm返回岐管體積m30.005Mv水蒸氣摩爾質(zhì)量kg/mol0.018MN2氮?dú)饽栙|(zhì)量kg/mol0.028MO2氧氣摩爾質(zhì)量kg/mol0.032Ma空氣摩爾質(zhì)量kg/mol0.029Φatm環(huán)境空氣的相對(duì)濕度0.5Ksm.out供應(yīng)管道孔口常數(shù)kg/(s·Pa)2×10-5Kca.ou陰極出口常數(shù)kg/(s·Pa)1×10-5mv.ca.max陰極側(cè)水蒸氣的最大質(zhì)量kg/mol0.0018yO2.atm氧氣摩爾分?jǐn)?shù)0.21yN2.atm氮?dú)饽柗謹(jǐn)?shù)0.79

3種控制方法參數(shù)見表A3。

表A3 3種控制方法參數(shù)

Table A3 Parameters of three control methods

方法陰極壓力控制KpKiKdλμFFM0.0041×10-61×10-40.60.9PPM0.002 51×10-61×10-4PPP0.002 51×10-61×10-4方法過氧比控制KpKiKdλμFFM20.11×10-80.50.01PPM15200PPP25200方法電機(jī)轉(zhuǎn)矩控制KpKiKd預(yù)測(cè)時(shí)域仿真步長(zhǎng)FFM14×10-6PPM14×10-6PPP0.90.851×10-4

燃料電池電堆參數(shù)為

V0=0.279-8.5×10-4(Tfc-298.15)+

Va=(-1.618×10-5Tfc+1.618×10-2)·

(-5.8×10-4Tfc+0.5736)

c1=10,c3=2,jmax=2.2 A/cm2

b11=0.051 39,b12=0.003 26,b2=350,

λm=14