同軸線總成S參數(shù)級(jí)聯(lián)計(jì)算模型
施冬李,孫 競(jìng),仇宗來(lái),潘嘯鐘,林橋水,余里浩
(泛亞汽車技術(shù)中心有限公司,上海 201201)
隨著汽車上傳輸?shù)臄?shù)據(jù)量越來(lái)越大,意味著時(shí)鐘頻率也將越來(lái)越高。汽車上連接模塊的導(dǎo)線長(zhǎng)度一般在1~10m之間,隨著信號(hào)頻率增大,信號(hào)的波長(zhǎng)也越來(lái)越短,信號(hào)的波長(zhǎng)與導(dǎo)線長(zhǎng)度比較接近,這時(shí)候信號(hào)的波動(dòng)性將在長(zhǎng)度上得到體現(xiàn)。
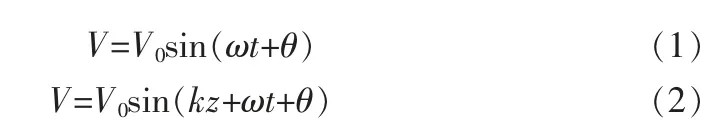
式中:V0——電壓幅值;k——傳播系數(shù),2π/λ;z——傳播方向的距離;ω——角速度;t——時(shí)間。
公式(1)代表低頻電壓變化關(guān)系,比如傳輸頻率為10kHz,傳輸?shù)膶?dǎo)線為10m,信號(hào)的波長(zhǎng)為30000m,kz=0.0021<<1,可忽略,所以電壓變化與時(shí)間相關(guān)[1]。
公式(2)代表高頻電壓變化關(guān)系,比如傳輸頻率變?yōu)?00MHz,傳輸?shù)膶?dǎo)線為10m,信號(hào)的波長(zhǎng)為3m,kz=20.9,這時(shí)候?qū)Ь€位置也會(huì)影響電壓的變化,所以電壓變化不僅與時(shí)間相關(guān),還與位置相關(guān),這個(gè)稱為長(zhǎng)線效應(yīng),即需要考慮由位置變化帶來(lái)的電壓電流的波動(dòng)性。
由公式(1)向公式(2)的轉(zhuǎn)換,盡管只增加了kz這一個(gè)變量,但是讓高頻導(dǎo)線發(fā)生了質(zhì)變,低頻導(dǎo)線主要考慮連接的可靠性,而高頻導(dǎo)線不僅需要滿足連接的可靠性,而且還需要考慮信號(hào)的品質(zhì)。如果不考慮這些性能,可能會(huì)導(dǎo)致各種模塊信號(hào)異常,比如黑屏、藍(lán)屏以及閃屏等問(wèn)題。
目前汽車上使用的同軸線越來(lái)越多,比如AMFM、GPS/Cell、V2X、數(shù)字?jǐn)z像頭等功能。實(shí)際應(yīng)用的同軸線在車上布置的長(zhǎng)度在增加,為了便于安裝,經(jīng)常需要增加inline連接器的數(shù)量,這些變更都會(huì)影響同軸線的S參數(shù)。在工程實(shí)際應(yīng)用中,對(duì)于S參數(shù)的插入損耗進(jìn)行線性累加相對(duì)精準(zhǔn),而回波損耗卻沒(méi)有一個(gè)很好的計(jì)算模型,所以需要研究下算法模型。
1 同軸線總成的電氣性能要求
1.1 特性阻抗
高頻信號(hào)從某種程度上講是一種電磁波,電磁波由磁場(chǎng)和電場(chǎng)組成,電場(chǎng)(等效為電壓)和磁場(chǎng)(等效為電流)的比值就是特性阻抗。
比如電磁波在空氣中傳輸也會(huì)有特性阻抗,一般稱為波阻抗,等于120π。
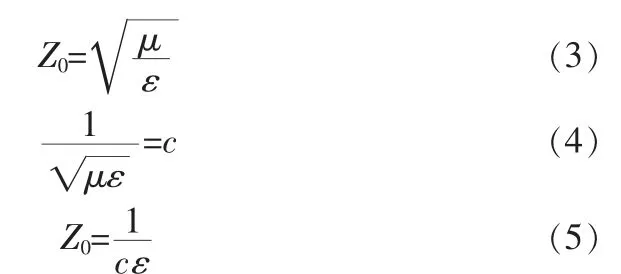
式中:μ——磁導(dǎo)率;ε——真空介電常數(shù);c——光速。
我們都知道,當(dāng)電磁波遇到不同介電常數(shù)的物質(zhì)時(shí)(比如水),會(huì)發(fā)生反射和折射。從公式(5)可以看出介電常數(shù)其實(shí)影響了電磁波傳輸?shù)奶匦宰杩梗噪姶虐l(fā)生反射和折射不是因?yàn)榻殡姵?shù)變了,而是特性阻抗變了。沒(méi)有反射的前提條件就是保持特性阻抗不變[1]。
電磁波在同軸線中傳輸時(shí)(一般是TEM波,電磁波的電場(chǎng)和磁場(chǎng)都在垂直于傳播方向的平面上的一種電磁波),它會(huì)像空氣中的電磁波一樣也有特性阻抗,公式如下(無(wú)耗同軸線,假設(shè)電磁能不會(huì)轉(zhuǎn)換成其他形式的能量)。它們的差別是電感對(duì)應(yīng)于磁導(dǎo)率,電容對(duì)應(yīng)于介電常數(shù)[1]。
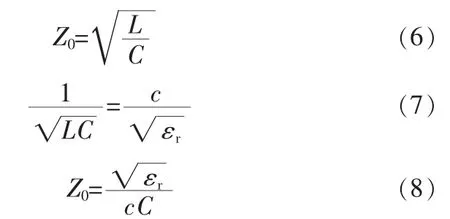
式中:L——單位電感;C——單位電容;c——光速;εr——相對(duì)介電常數(shù)。
對(duì)電感和電容進(jìn)一步細(xì)化,得到如下無(wú)耗同軸線的特性阻抗公式[1]:
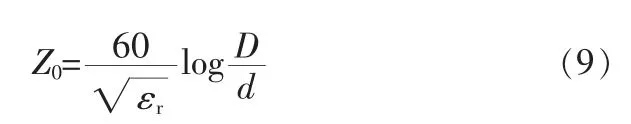
式中:εr——相對(duì)介電常數(shù);D——同軸線屏蔽層的直徑;d——中心導(dǎo)體的直徑。
為了確保傳輸?shù)碾姶挪ú话l(fā)生反射,需要保證同軸線特性阻抗處處相等。根據(jù)公式(9)發(fā)現(xiàn),特性阻抗與同軸線的絕緣體的介電常數(shù)有關(guān),還和中心導(dǎo)體和屏蔽層的直徑之比強(qiáng)相關(guān)。在實(shí)際產(chǎn)品中,連接器是很難做到特性阻抗匹配,原因有兩個(gè):①連接器內(nèi)部存在空氣,介電常數(shù)存在波動(dòng);②由于使用端子壓接工藝,連接器內(nèi)部D/d無(wú)法等于恒值。Fakra連接器剖面圖如圖1所示。
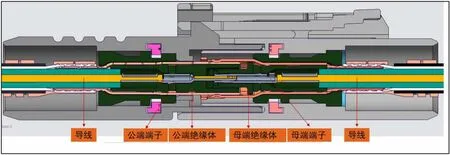
圖1 Fakra連接器剖面圖
通過(guò)網(wǎng)絡(luò)分析實(shí)測(cè)1.2m長(zhǎng)同軸線總成,特性阻抗的突跳值都在連接器的位置。如圖2所示。X軸代表信號(hào)往前傳輸?shù)臅r(shí)間,單位ns;Y軸代表特性阻抗值。
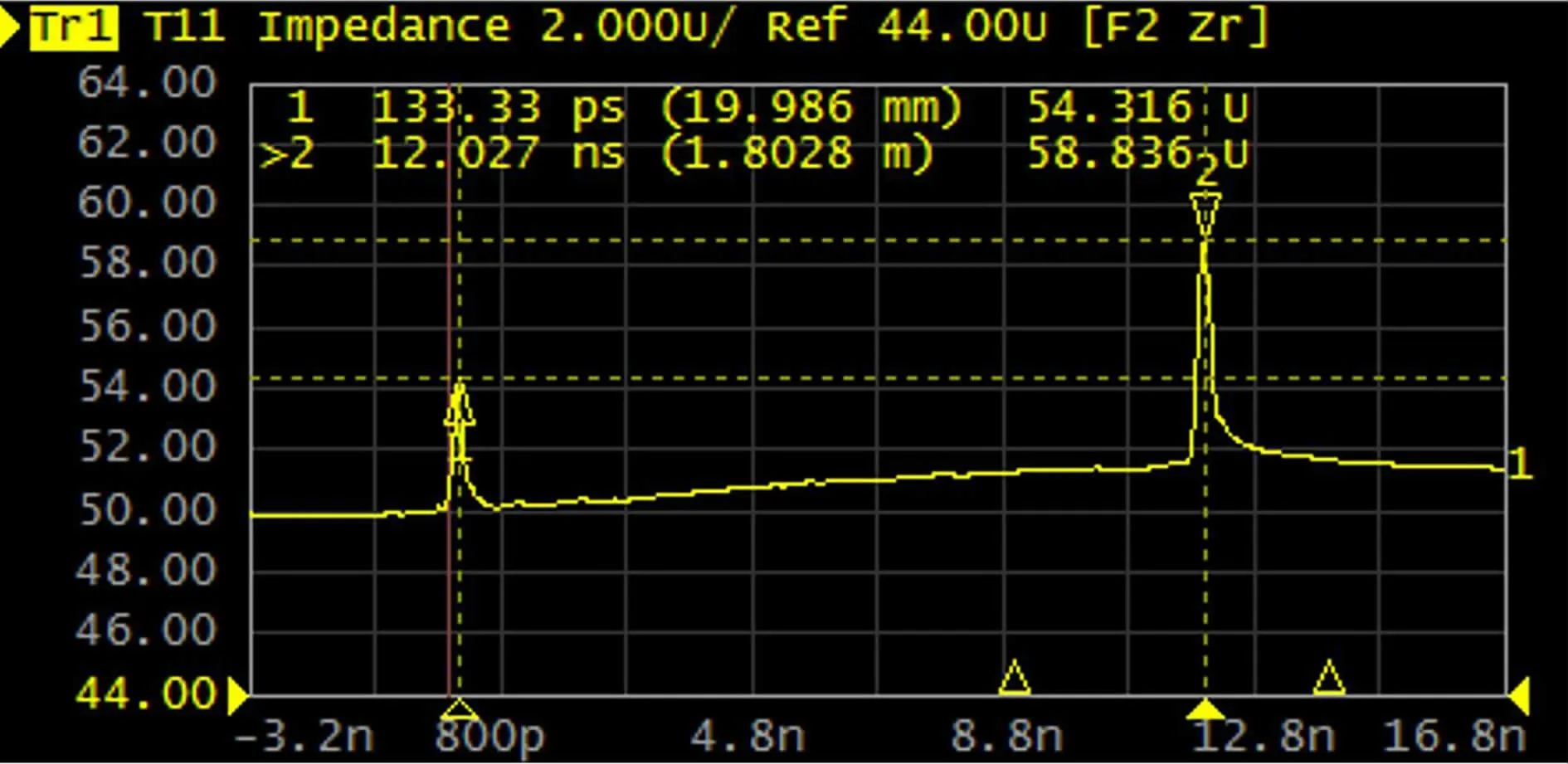
圖2 特性阻抗測(cè)量(特性阻抗值一般要求為50Ω或75Ω)
電磁波的反射存在如下危害:①減少傳輸功率(或電壓);②在電壓波形的上升沿和下降沿形成震蕩。所以需要評(píng)估特性阻抗對(duì)同軸線電氣性能的影響。
1.2 S參數(shù)
特性阻抗無(wú)法量化分析同軸線總成的電氣性能。如果要量化分析同軸線總成的電氣參數(shù),需要使用S參數(shù)來(lái)進(jìn)行評(píng)估。
電磁波有兩種形態(tài):一種是入射波a,一種是反射波b。同軸線總成有輸入和輸出兩種狀態(tài),屬于二端口網(wǎng)絡(luò):端口1和端口2。那么同軸線的S參數(shù)如圖3所示[1]。
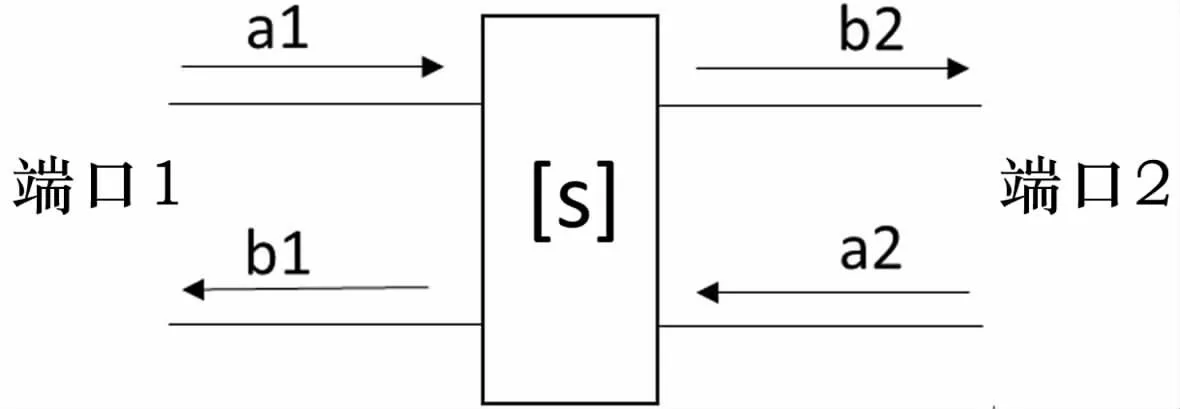
圖3 同軸線S參數(shù)框圖
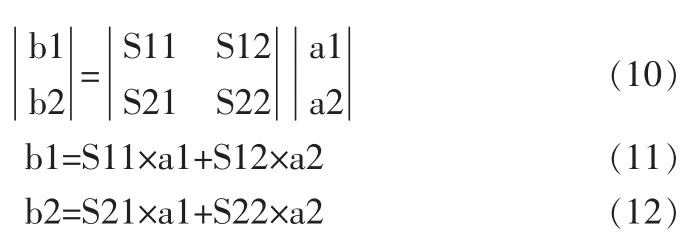
S12代表1端口在匹配的情況下(a1=0)的插入損耗:S12=10lg(b1和a2代表功率)或者S12=20lg(b1和a2代表電壓幅值)。
S11代表2端口在匹配的情況下(a2=0)的回波損耗:S11=10lg(b1和a1代表功率)或者S11=20lg(b1和a1代表電壓幅值)。
對(duì)多根同軸線總成進(jìn)行S參數(shù)級(jí)聯(lián)計(jì)算時(shí),插入損耗一般可通過(guò)線性累加的方式進(jìn)行計(jì)算:S12=S12+_S12。注:S參數(shù)的單位是dB(如果是比值,那就是S12=S12×_S12)。
這種算法和實(shí)際測(cè)試結(jié)果誤差很小。如果你用同樣的方法對(duì)回波損耗進(jìn)行計(jì)算時(shí),就會(huì)發(fā)現(xiàn)誤差很大,原因?yàn)椋悍瓷洳ㄑ卦窂絺鞑r(shí)也會(huì)受到插入損耗的影響而變小,到下一個(gè)阻抗不匹配點(diǎn)還會(huì)發(fā)生第2次反射,反射波又變小了一點(diǎn)。回波損耗根本無(wú)法通過(guò)線性累加獲取。如圖4所示。

圖4 回波損耗在同軸線中衰減反射示例
1.3 鏈路的性能要求
對(duì)于模塊和模塊之間通信,收發(fā)器的芯片會(huì)對(duì)其所用同軸線總成的電氣性能有所要求。比如:芯片型號(hào)DS90UBX XXX&DS90UBXXXX會(huì)對(duì)Coax Cable提出相關(guān)的電氣性能要求,注意這里的速率單位都是Hz,而不是b/s。實(shí)際應(yīng)用時(shí)需要模塊輸入芯片型號(hào),以及具體應(yīng)用的時(shí)鐘頻率是多少。表1為S參數(shù)性能要求。

表1 S參數(shù)性能要求
在項(xiàng)目早期選型的時(shí)候,需定義同軸線總成的inline連接器的數(shù)量,inline連接器會(huì)增加阻抗不匹配點(diǎn),所以需要建立同軸線級(jí)聯(lián)S參數(shù)模型,從而確保滿足系統(tǒng)要求。
2 同軸線S參數(shù)計(jì)算模型
S參數(shù)級(jí)聯(lián)可通過(guò)信號(hào)流圖的方法進(jìn)行計(jì)算[1](借助拓?fù)鋱D形求線性代數(shù)方程組解的一種方法。由S.J.梅森提出,又稱梅森圖)。同軸線的S參數(shù)可以轉(zhuǎn)換成圖5所示的拓?fù)潢P(guān)系圖,a1和a2代表輸出節(jié)點(diǎn),b1和b2代表輸出節(jié)點(diǎn)。S11代表有a1節(jié)點(diǎn)流向b1節(jié)點(diǎn),S21代表a1節(jié)點(diǎn)流向b2節(jié)點(diǎn),S22代表a2節(jié)點(diǎn)流向b2節(jié)點(diǎn),S12代表a2節(jié)點(diǎn)流向b1節(jié)點(diǎn)。
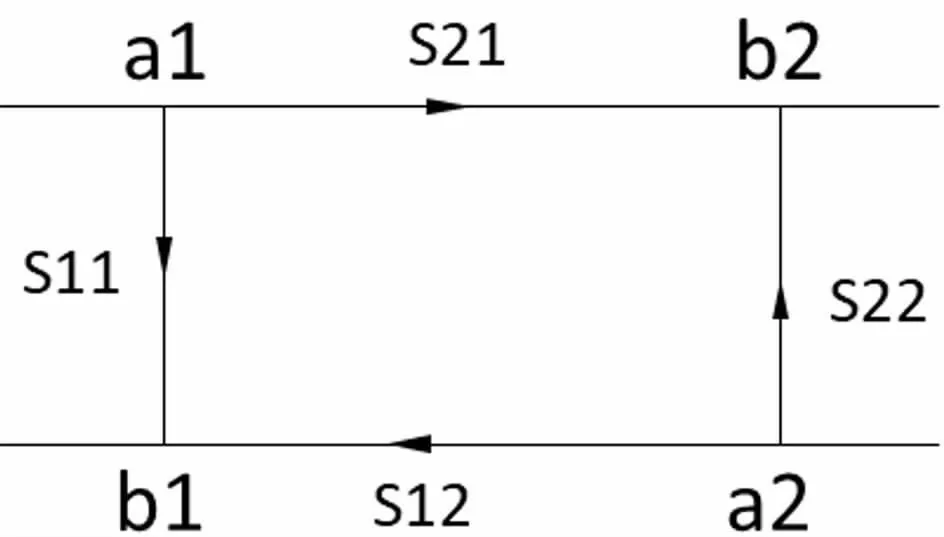
圖5 同軸線S參數(shù)拓?fù)?/p>
如果2根同軸線進(jìn)行連接,那么它們的拓?fù)潢P(guān)系如圖6所示(為了表示2根同軸線的區(qū)別,另外一根同軸線的節(jié)點(diǎn)和S參數(shù)前都增加“_”)。b2節(jié)點(diǎn)和_a1節(jié)點(diǎn)重合,以b2來(lái)表示;a2節(jié)點(diǎn)和_b1節(jié)點(diǎn)重合,以a2來(lái)表示。
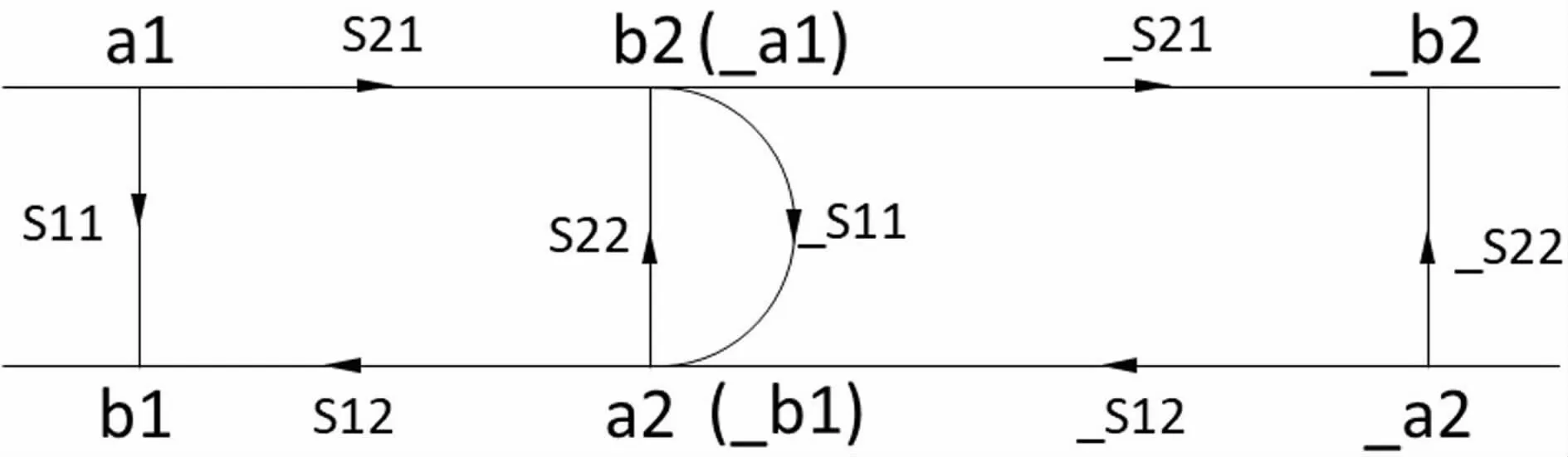
圖6 級(jí)聯(lián)同軸線S參數(shù)拓?fù)?/p>
圖7為信號(hào)流圖運(yùn)算法則示意。
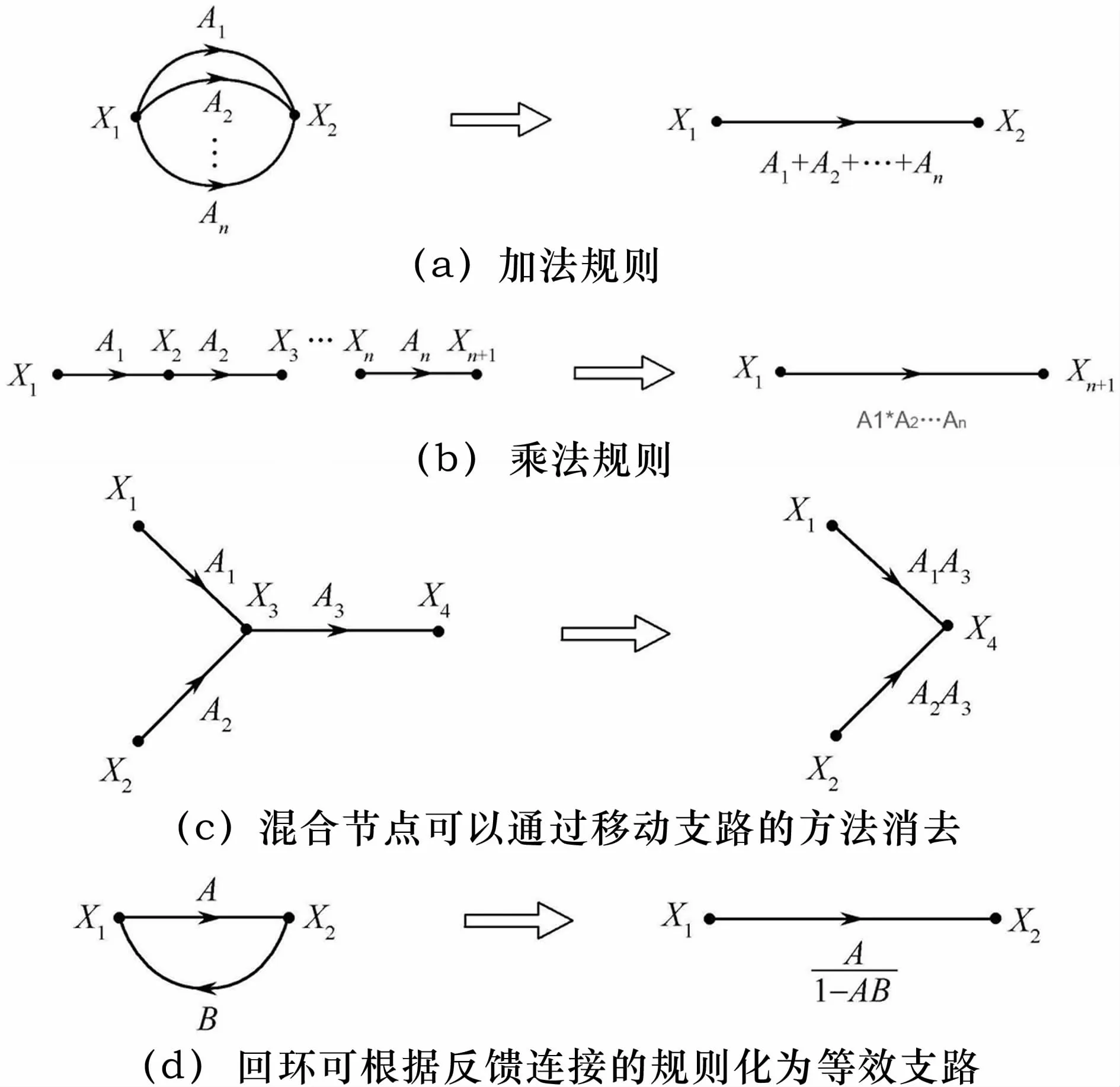
圖7 信號(hào)流圖運(yùn)算法則示意
1)加法規(guī)則:n個(gè)同方向并聯(lián)支路的總傳輸,等于各個(gè)支路傳輸之和。
2)乘法規(guī)則:n個(gè)同方向串聯(lián)支路的總傳輸,等于各個(gè)支路傳輸之積。
3)混合節(jié)點(diǎn)可以通過(guò)移動(dòng)支路的方法消去。
4)回環(huán)可根據(jù)反饋連接的規(guī)則化為等效支路。
根據(jù)信號(hào)流圖運(yùn)算法則,可得到如下4個(gè)恒等式:
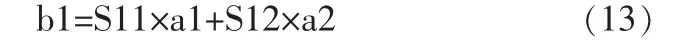
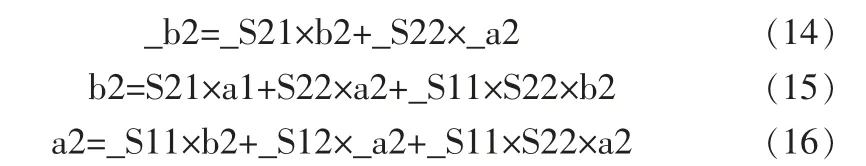
對(duì)這4個(gè)恒等式進(jìn)行整理得到如下2個(gè)恒等式:
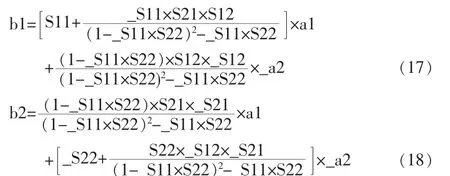
級(jí)聯(lián)后的S參數(shù)如下:
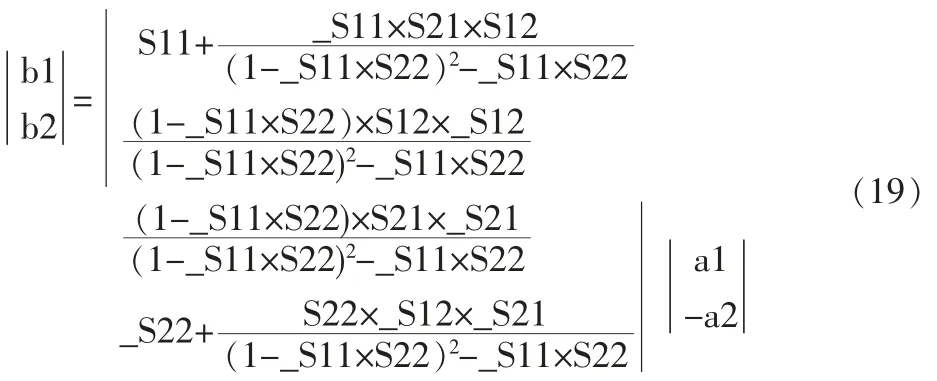
由于S21和S12是對(duì)稱的,S11和S22也是對(duì)稱的,所以只要分析清楚S11和S21,按同樣的原理可分析S22和S12(級(jí)聯(lián)后的S參數(shù)增加下劃線來(lái)區(qū)分)。
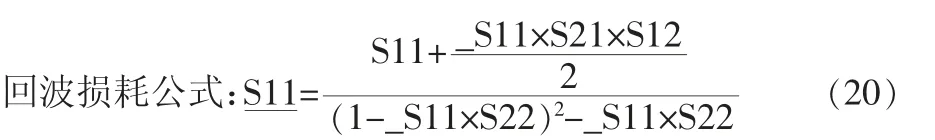
S11是在2端匹配的情況下的b1/a1比值。在級(jí)聯(lián)模式下,a1有兩條路徑可以走:路徑1即S11的方向,這可以解釋為何等式中有S11;路徑2即S21到_S11,再到S12的方向,這可以解釋為何等式第二式中的分子等于_S11×S21×S12。圖8為回波損耗傳遞路徑。
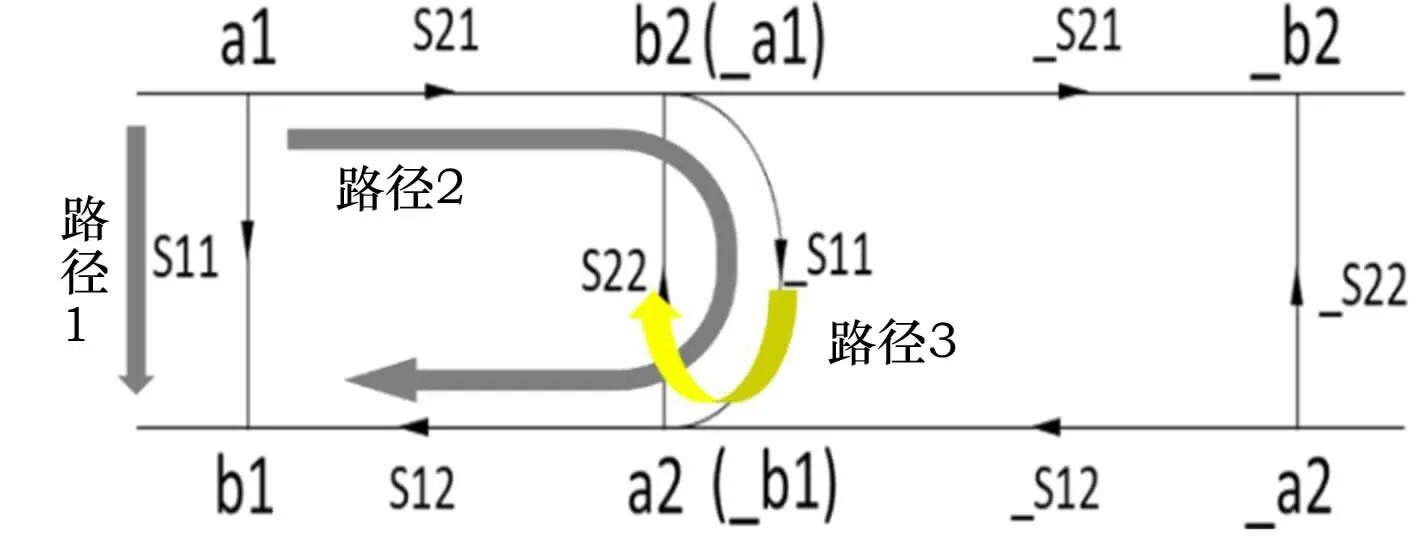
圖8 回波損耗傳遞路徑
那么為何還有分母這么奇怪的等式呢?真實(shí)情況是還存在一條潛在路徑3即_S11到S22。這是一個(gè)不斷反射循環(huán)的回路:_S11的一部分能量走到S22,在節(jié)點(diǎn)b2又有一部分回到_S11,接著又開(kāi)始上面的循環(huán)。這樣周而復(fù)始,無(wú)限循環(huán)下去。針對(duì)這種循環(huán),有如下類似數(shù)學(xué)公式進(jìn)行歸納:=1+α+α2+α3……(當(dāng)α遠(yuǎn)遠(yuǎn)小于1時(shí))。
_S11×S22當(dāng)滿足遠(yuǎn)遠(yuǎn)小于1,也有類似的公式,所以分母(1-_S11×S22)2-_S11×S22表示的就是反射波不斷反射循環(huán)的過(guò)程。
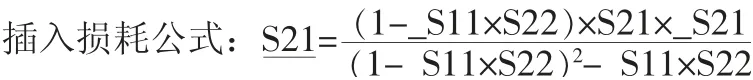
S21是在2端匹配的情況下的b2/a1比值。S21有路徑1和潛在路徑2。路徑1表達(dá)式為S21×_S21,潛在路徑2是電磁波不斷反射循環(huán)的過(guò)程,用來(lái)表示。當(dāng)_S11×S22遠(yuǎn)遠(yuǎn)小于1時(shí),S21≈S21×_S21(即20lgS21=20lgS21+20lg_S21),這也可以成為為何插入損耗通過(guò)線性累加其精度仍然挺準(zhǔn)確的原因。圖9為插入損耗傳遞路徑。
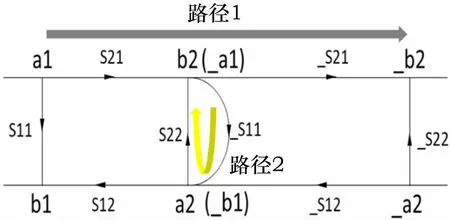
圖9 插入損耗傳遞路徑
3 計(jì)算模型驗(yàn)證
制作了0.5m,1m,1.5m,2m,3m,4m,5m以及6m同軸線,進(jìn)行了如表2所示兩兩連接的驗(yàn)證矩陣。

表2 同軸線級(jí)聯(lián)模型驗(yàn)證矩陣
測(cè)試的頻率范圍:0~3GHz,理論計(jì)算值和網(wǎng)絡(luò)分析儀比較結(jié)果如圖10~圖13、表3和表4所示(0.5m和1m的實(shí)驗(yàn)結(jié)果比較)。
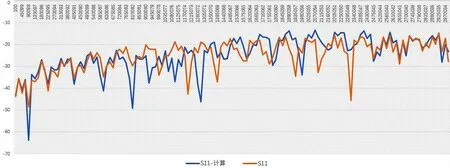
圖10 S11計(jì)算值和理論值結(jié)果對(duì)比
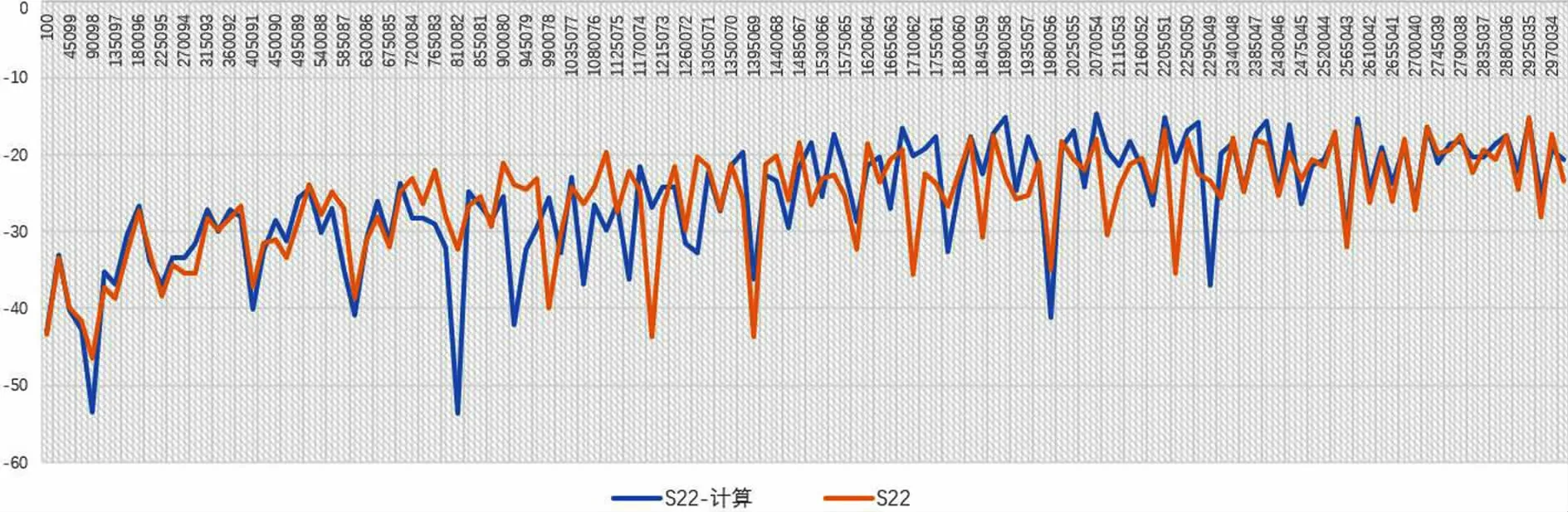
圖11 S22計(jì)算值和理論值結(jié)果對(duì)比
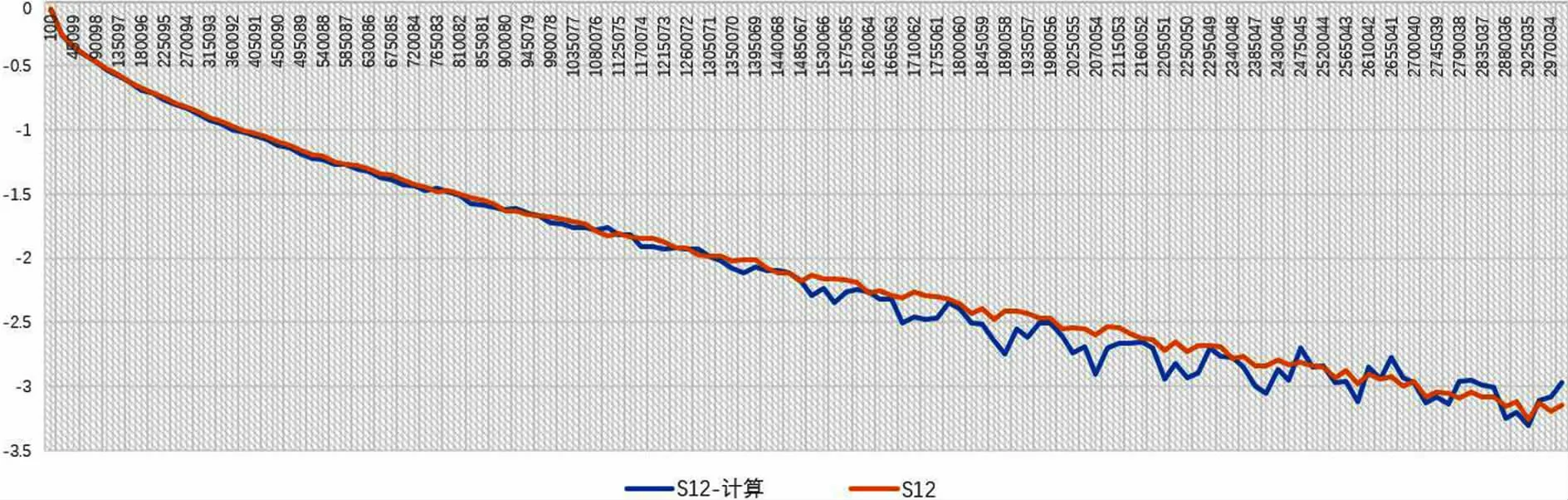
圖12 S12計(jì)算值和理論值結(jié)果對(duì)比

圖13 S21計(jì)算值和理論值結(jié)果對(duì)比
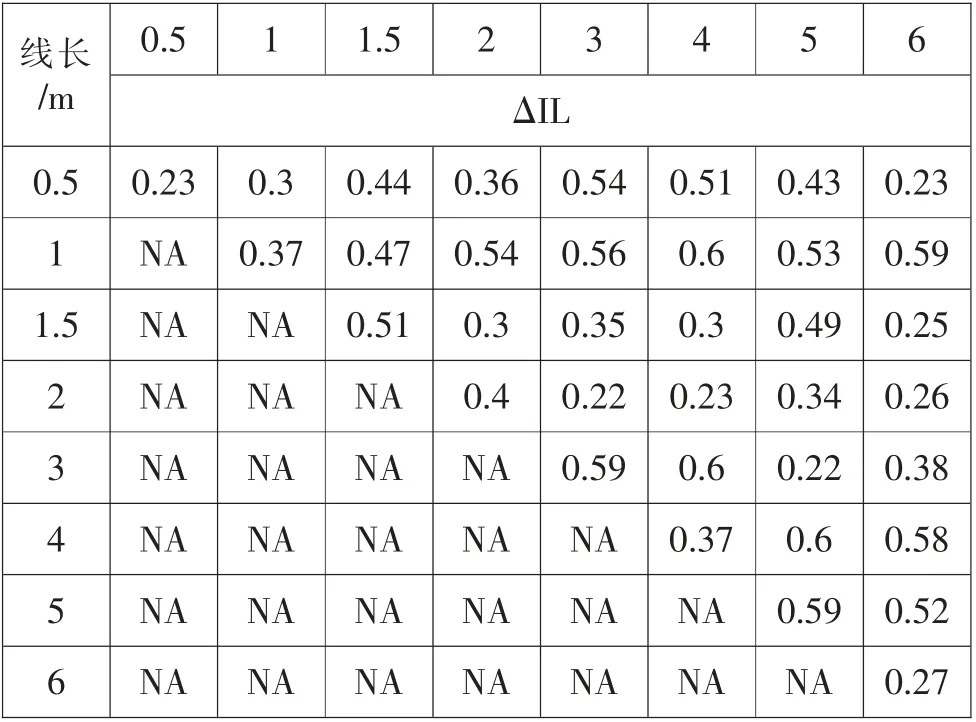
表3 同軸線級(jí)聯(lián)模型插入損耗驗(yàn)證結(jié)果
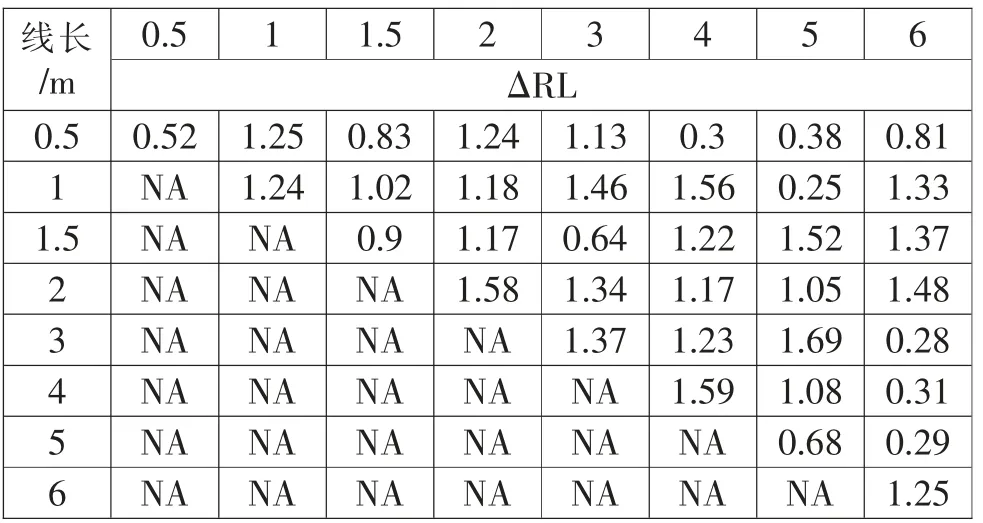
表4 同軸線級(jí)聯(lián)模型回波損耗驗(yàn)證結(jié)果
理論計(jì)算和實(shí)際結(jié)果之間還是存在偏差,IL最大偏差值0.6dB,RL最大偏差1.75dB。在項(xiàng)目早期可通過(guò)此算法進(jìn)行S參數(shù)的估算,后期再通過(guò)實(shí)物樣件在網(wǎng)絡(luò)分析儀中進(jìn)行實(shí)測(cè)[2]。
4 結(jié)語(yǔ)
同軸線的S參數(shù)的計(jì)算:級(jí)聯(lián)后的插入損耗,只要系統(tǒng)中回波損耗不是特別大(即_S11×S22遠(yuǎn)遠(yuǎn)小于1),那么簡(jiǎn)單地對(duì)插入損耗進(jìn)行線性累加,其準(zhǔn)確度比較高。
但對(duì)于級(jí)聯(lián)后的回波損耗,如果直接進(jìn)行線性累加,誤差會(huì)很大,這是由于回波損耗還受到插入損耗和二次反射的影響。所以在實(shí)際工程應(yīng)用中一定需要注意回波損耗千萬(wàn)不能線性疊加。有時(shí)候?qū)Ь€加長(zhǎng),還會(huì)減小回波損耗。

