基于粒子群算法的自動駕駛儀參數優化
張田田, 陳志華, 韓 磊, 賈 芳
(1.南京理工大學 瞬態物理國家重點實驗室, 南京 210094; 2.中國兵器工業導航與控制技術研究所,北京 100089; 3.中國兵器第三○四廠,山西 長治 046012)
1 引言
導彈的制導控制系統是實現導彈擊毀目標的關鍵[1]。自動駕駛儀是制導控制系統中至關重要環節[2],確保導彈精確、魯棒地跟蹤制導系統生成的控制指令是它的核心任務[3]。對于新一代近距空空格斗導彈,要求其具有很高的機動性[4-5],要求在保持穩定性的同時快速響應加速度指令,提供大機動性[6-7]。加速度計與質心距離參量c是設計自動駕駛儀需要考慮的重要因素。現有的研究中,對于參量c的處理主要有3種:一是直接忽略它的影響[8];二是對其合理利用[9];三是設計中引用濾波器消除參量c的影響[10]。參量c對于控制輸入舵偏、系統響應速度、系統的穩定性都有重要影響,忽略c不僅會導致系統響應慢、穩定裕度低,而且會導致對舵偏需求過高。系統需要的舵偏越大,對舵機的要求就越高,這將在一定程度上影響導彈的控制效果。目前對參量c的研究較少,且未能與粒子群尋優算法設計緊密結合以實現系統整體控制性能最優。
2 基于擴展LQR的自動駕駛儀設計
俯仰自動駕駛儀的設計將被設定為一個LQR最優控制問題,需要對“標準”LQR問題進行擴展,包括目標中的前饋項、輸出反饋等。
對于采用軸對稱布局的導彈,俯仰和偏航運動方程相似,只有符號正負性不同,所以下面用俯仰通道為例進行研究,其控制方程組可表示為:
(1)
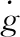
標準的LQR問題不考慮Du項,本文引入Du項設計自動駕駛儀;自動駕駛儀的設計屬于LQR跟蹤問題,,對于階躍指令,跟蹤問題可轉為定點調節問題[11]。
給出狀態空間
(2)
式中:ayc、ay分別表示過載指令和輸出過載;KDC閉環增益調節系數;V為彈體速度。
H=[Vbδ-caδ-caω],L=[Vbδ-caδ]
以“消除過載誤差、減少舵偏輸入”為控制目標,建立LQR調節器問題的目標函數
(3)
基于式(3)構造Hamilton函數,并做出以下假設:
假設1:u無約束;
假設2:最優性能指標具有二次型的形式;
參照文獻[12]可以得到最優輸出反饋控制率u*
u*=-(I+FoptD)-1Fopt(Cx-[KDC0]Tayc
(4)
式中:Fopt為輸出反饋矩陣。
為了使系統能夠精確跟蹤加速度指令,需確定調節系數KDC。
將式(4)代入狀態空間(2),根據終值定理
(5)
得到
(6)
式中:
其中“×”表示該矩陣與(I+FoptD)-1Fopt相乘,例L×表示L(I+FoptD)-1Fopt。
3 粒子群算法
3.1 優化目標數學模型
為了提高彈體響應速度、減少舵偏輸入、改善阻尼,選用調節時間t、超調量γ、舵偏角δε構成目標函數。其中,調節時間表示系統的響應,超調量表示系統的阻尼[13]。為了保證姿態控制系統的穩定性,一般情況,選取幅值裕度Gm>6 dB,相位裕度Pm>30 rad/s。同時為了簡化優化過程,避免參量相互影響,引入權重系數a1、a2、a3將多目標優化轉化為單目標優化。圖1為優化目標函數圖形,用顏色表示第四維函數值f。
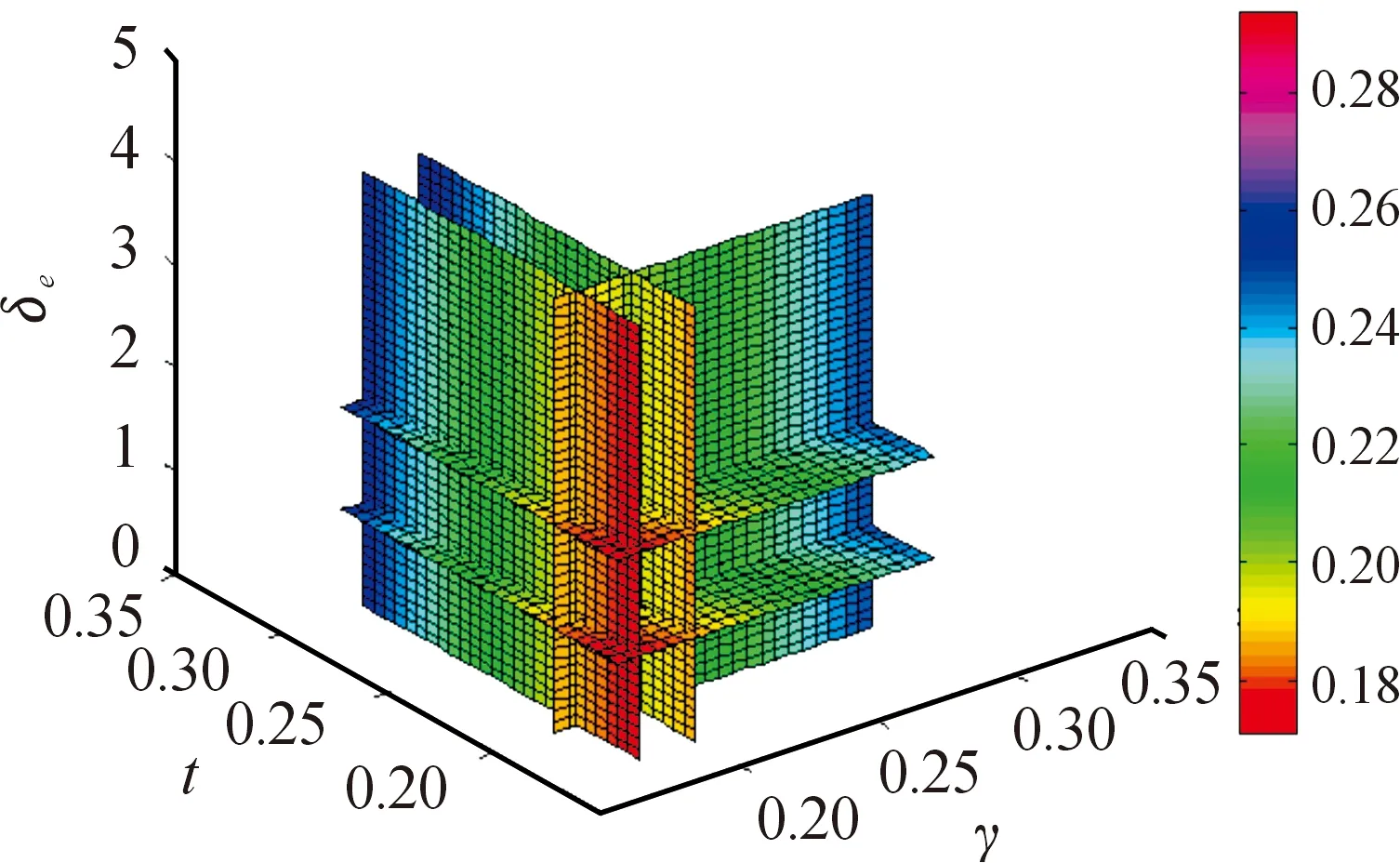
圖1 優化多目標模型函數圖形
(7)
式中:a1、a2、a3分別代表γ、t、δε的權重系數。
3.2 粒子群算法優化流程
文獻[14]給出加速度計與質心距離參量c的約束范圍,在試驗過程中發現,參量c過大會導致實際穿越頻率與期望穿越頻率偏差過大,參量c偏小會導致系統穩定裕度極低,進而影響系統的穩定性。出于工程上實際應用的考慮,綜合彈體結構布局、彈性等多方面因素,本文選取c在[-1,1]的約束范圍。
步驟1:采用Matlab指令rands隨機生成初始化粒子和粒子速度,種群規模選擇50;
步驟2:采用式(7)計算每個粒子的適應度,選取個體的局部最優位置向量Pgj種群的全局最優位置向量Pzj;
步驟3:采用式(8)更新粒子位置和速度;
Vj=Vj+C1rand(Pgj-Xj)+C2rand(Pzj-Xj)
Xj=Xj+0.5Vj
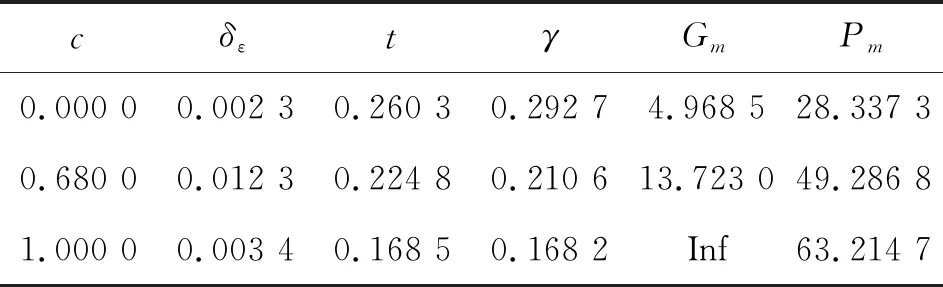
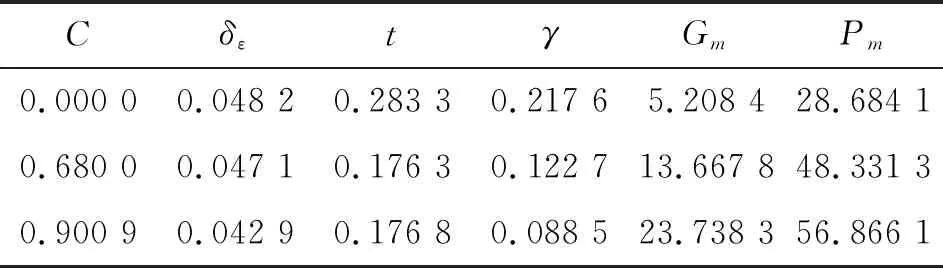
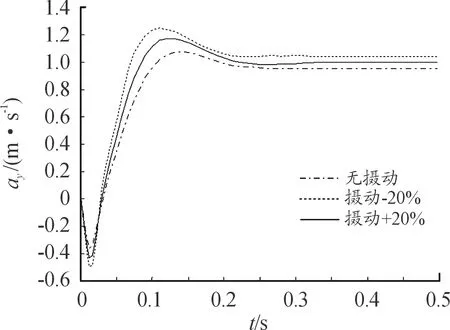
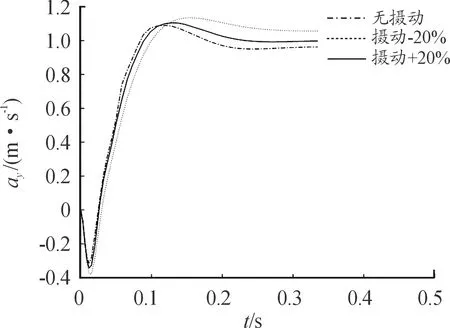
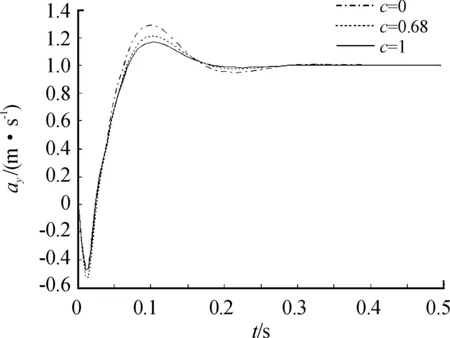
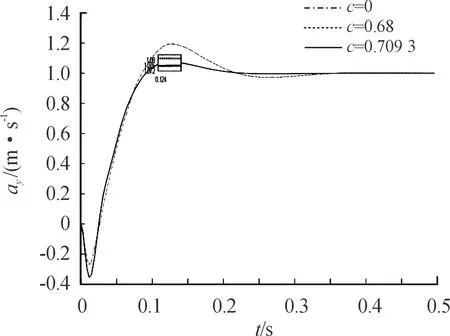
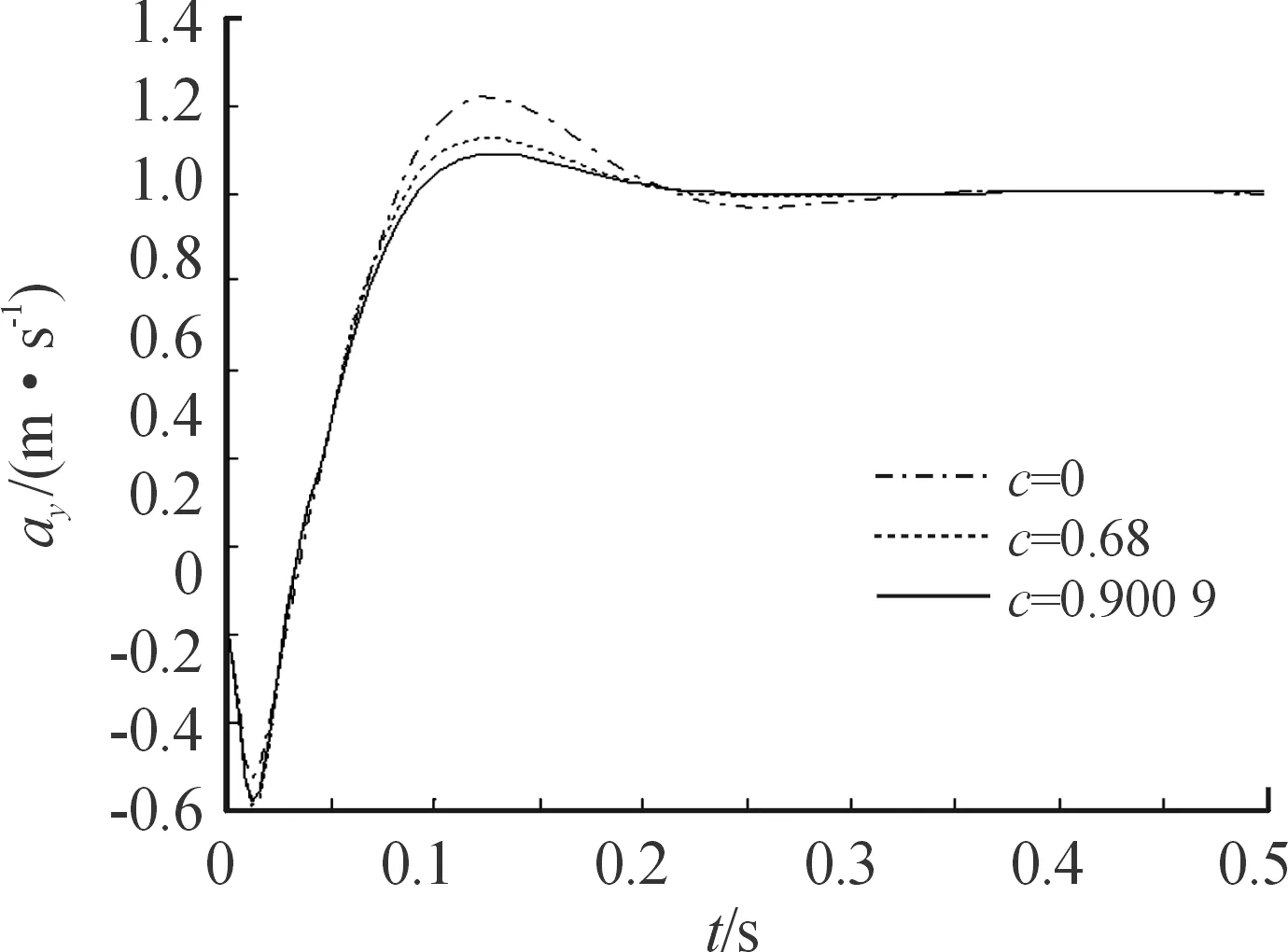
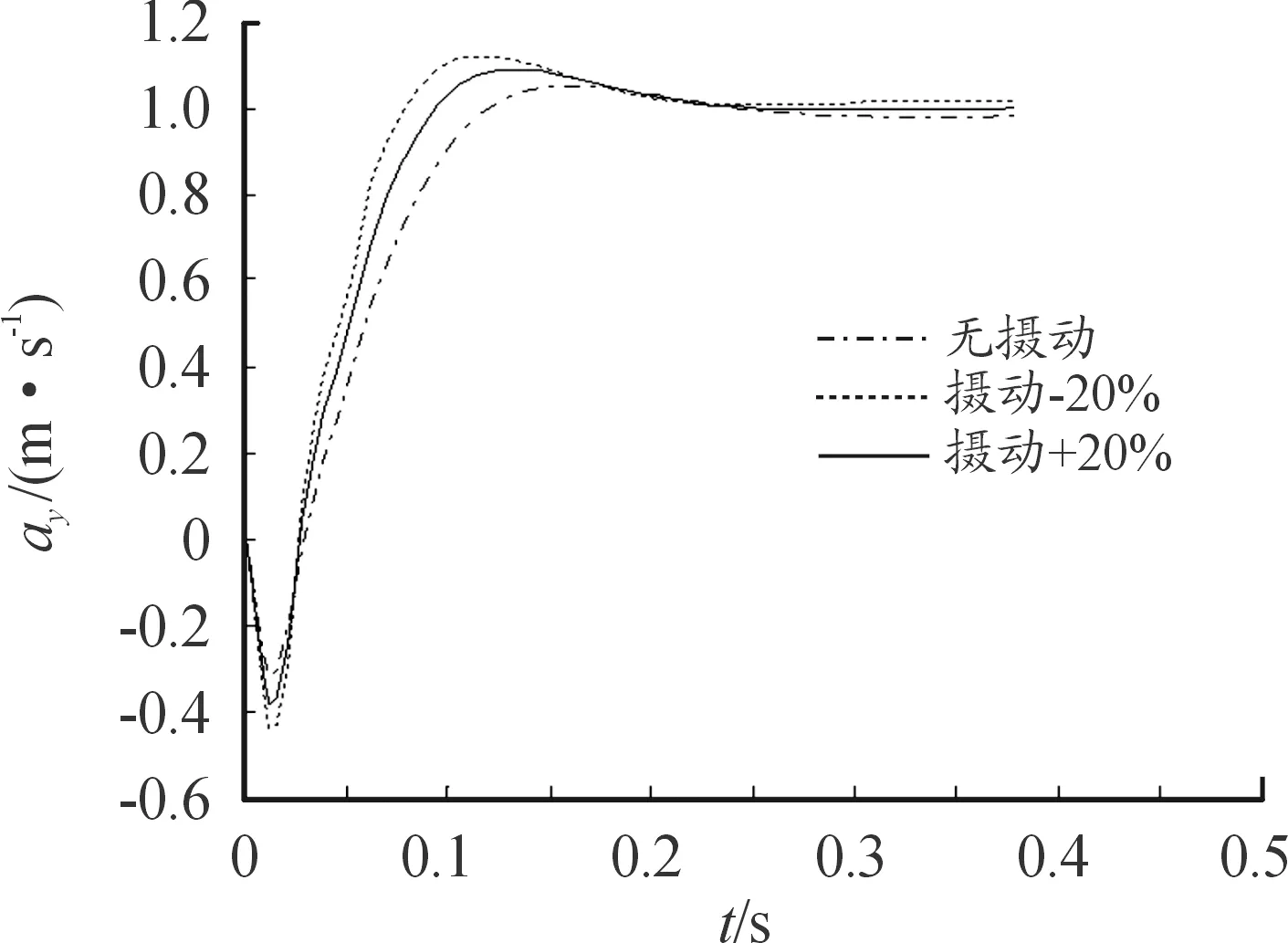
-1 -1 (8) 式中:C1=C2=1.494 45 步驟4:基于步驟3更新的種群,采用式(8)重新計算粒子適應度,判斷是否滿足終止條件,若不滿足,返回步驟2; 步驟5:選取迭代次數為50,當達到迭代次數終止迭代。 圖2 粒子群算法優化流程框圖 本文以某空空導彈的某一特征點為例進行仿真分析,該特征點動力系數如表1所示。設開環穿越頻率為WCR=45 rad/s,舵機頻率ω=220 rad/s,阻尼ζ=0.65。靜穩定彈體aα=250靜中立aα=0靜不穩定彈體aα=-250。 表1 特征點動力系數 表2給出LQR加權陣選值,選取恰當的加權陣可以使系統達到期望的WCR。 表2 LQR加權陣選值 補充說明: c=0:表示忽略距離參量; c=0.68:表示距離參量c的一般取值; 下面分別對靜穩定彈體、靜中立穩定彈體、靜不穩定彈體優化結果進行分析。 1) 表3為靜穩定彈體的粒子群算法優化結果。c=1,表示優化后的距離參量c的取值。分析表3數據可知,優化后減少72%舵偏角,超調量從21.1%優化到16.8%,調節時間從0.23 s優化到0.17 s。而且穩定裕度也有大幅度的上升,幅值裕度從13.7 dB上升到Inf dB,相角裕度從49 rad/s上升到63 rad/s。 表3 靜穩定粒子群優化結果 2) 表4為靜不穩定彈體的粒子群算法優化結果。c=0.709 3,表示優化后的距離參量c的取值。分析表4數據可知,優化后減少約為1%舵偏角,超調量從8%下降到7%,調節時間幾乎不變。穩定裕度也小福度上升,幅值裕度從12.3 dB上升到13.2 dB,相角裕度從44 rad/s上升到46 rad/s。 表4 靜不穩定粒子群優化結果 3) 表5為靜中立穩定彈體的粒子群優化結果。c=0.900 9,表示優化后的距離參量c的取值。分析表5數據可知,雖然優化后調節時間有小幅度的上升,從0.176 3 s上升到0.176 8 s,但在超調量,舵偏方面有明顯的優化效果。 表5 靜中立穩定粒子群優化結果 優化后,超調量從12%優化到8%,舵偏減少8.9%。而且,穩定裕度也有大幅度的上升,幅值裕度從13.6 dB上升到23.7 dB,相角裕度從48 rad/s上升到57 rad/s。 上述分析都是基于優化后距離參量與一般情況c=0.68,可以直觀地看出,忽略距離參量c并不是一個很好的選擇。事實上,在自動駕駛儀設計中考慮c,即在加速度計測量信息中引入彈體姿態角加速度信息,相當于回路含有一個微分環節,具有超前作用,通常稱為加速度計的“杠桿效應”[15]。距離參量c的取值越大,c回路超前作用越明顯,系統越穩定,超調越小。 導彈氣動參數攝動會引起模型的變化[16],分析基于粒子群設計的自動駕駛儀在氣動參數偏差±20%輸出響應。 1) 靜穩定彈體參數攝動輸出響應曲線如圖3所示。 圖3 靜穩定參數攝動輸出響應曲線 氣動參數攝動+20%,穩態輸出偏差4.9%。氣動參數攝動-20%,穩態輸出偏差5.9%。 2) 靜不穩定彈體參數攝動輸出響應曲線如圖4所示。氣動參數攝動+20%,穩態輸出偏差3.6%。氣動參數攝動-20%,穩態輸出偏差6%。 圖4 靜不穩定參數攝動輸出響應曲線 3) 靜中立穩定彈體參數攝動輸出響應曲線如圖8所示。氣動參數攝動+20%,穩態輸出偏差1.2%。氣動參數攝動-20%,穩態輸出偏差1.8%。 圖3~圖8可以看出,優化結果可以快速響應加速度指令,并較好地抑制氣動參數變化。 圖5 靜穩定優化前后輸出響應曲線 圖6 靜不穩定優化前后輸出響應曲線 圖7 靜中立穩定優化前后輸出響應曲線 圖8 靜中立穩定參數攝動輸出響應曲線 本文在綜合考慮舵偏、穩定性、響應特性等方面的情況下,分析不同加速度計與質心距離參量對駕駛儀性能的影響,并結合粒子群算法尋求到最優距離參量。研究表明,基于粒子群優化算法設計的自動駕駛儀需求更小的舵偏,降低對彈體結構的需求,并在穩定性、響應特性方面也有大幅度提高,能夠較好地抑制氣動參數變化,在工程上也具有實用性。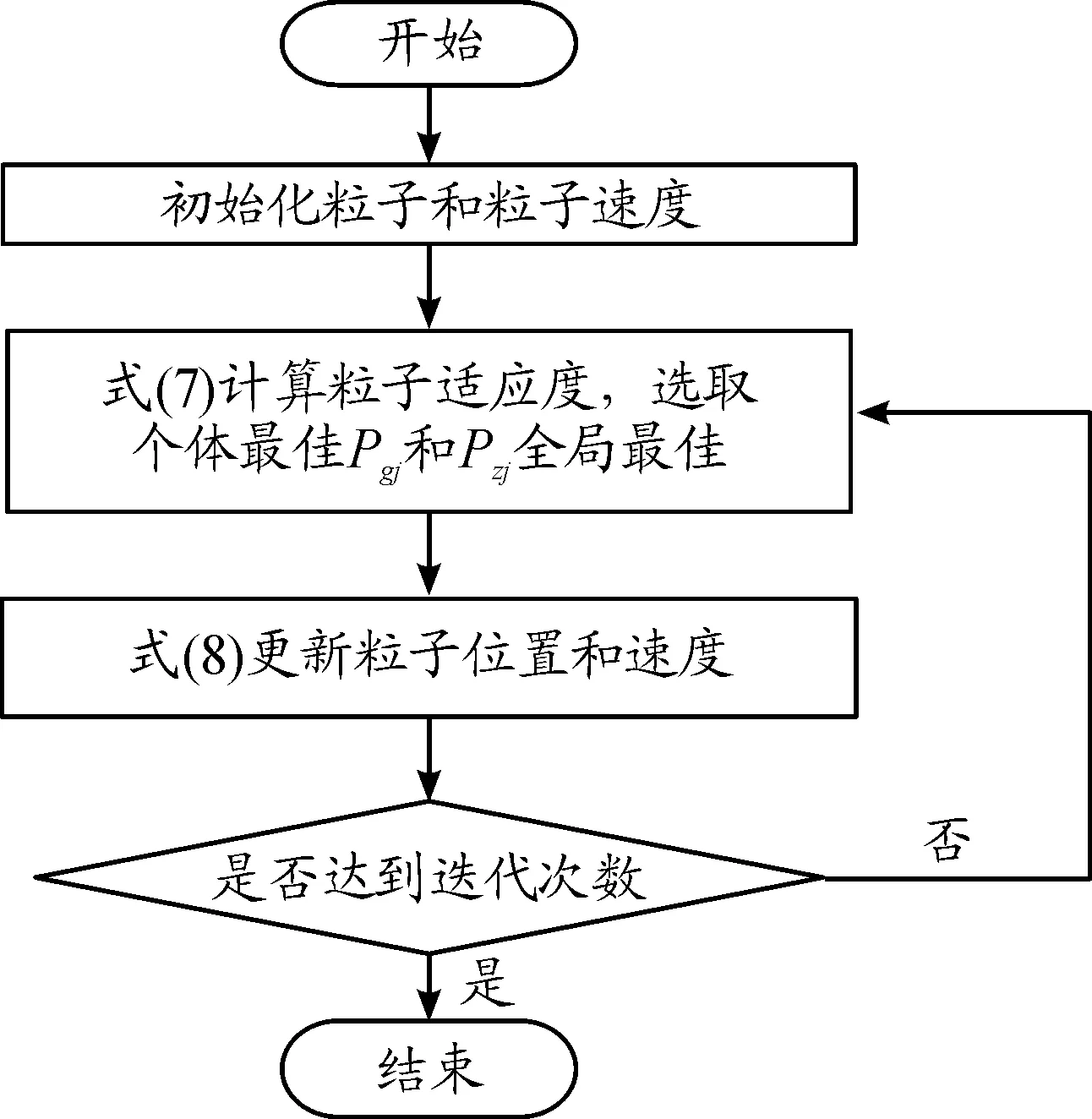
4 仿真分析
4.1 特征點仿真分析
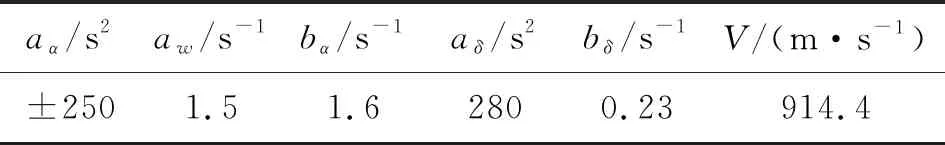


4.2 參數攝動分析
5 結論

