裂縫對太陽能儲熱圓棒混凝土熱性能的影響
朱慧君,匡 蕘,劉光鵬
(東南大學 能源與環境學院,南京 210096)
目前,太陽能儲熱材料主要分為顯熱材料、潛熱材料和化學材料[1-3]。顯熱材料包括液體材料(如熔鹽、導熱油等)和固體材料(如砂、巖石、高溫混凝土等)[4-5]。混凝土的化學性能穩定、儲熱能力好、工作范圍寬,并且每儲熱1 kW的成本在所有儲熱材料中最低,因此成為太陽能熱發電的理想儲熱材料之一[1,6-7]。
混凝土在生產過程中會產生裂縫,這是無法避免的原始性缺陷。裂縫的主要影響因素有溫度、原材料、塑性收縮裂縫等[8]。高溫儲熱混凝土在放熱過程經歷較大的溫度變化,熱應力將是影響裂縫進一步發展的最主要因素。溫度的大幅度變化造成裂縫處的熱應力增加甚至超過極限開裂值,將會二次破壞混凝土的內部結構[9-10]。目前,對于混凝土裂縫的研究主要是定性分析。唐世斌等[11]通過對混凝土導熱過程中熱應力進行特征分析,得到溫度梯度與熱膨脹不匹配時熱應力極容易導致混凝土開裂,同時開裂過程與導熱系數密切相關;XIN J D等[12]通過實驗研究了溫度變化和約束程度對早期混凝土開裂行為的影響,建立約束程度與溫差的關系,評估混凝土開裂的風險;BERTELSEN I M G等[13]在實驗室規模上評估了混凝土中纖維對表面開裂程度的影響,得到纖維特性對控制裂紋形成有積極影響;RAJEEV P等[14]通過開發有限元模型,量化參數研究混凝土磚材料性能和熱負荷的影響,發現磚內外表面溫差與裂縫寬度呈正相關性;SHEN L等[15]基于熱力學原理和混凝土破壞塑性,提出了一種在室溫下具有特征性的熱力學耦合模型,研究在裂縫熱阻的效應下混凝土應力分布的情況。但是,對于裂縫的具體形狀和尺寸與混凝土內部裂縫的溫度梯度關系,仍未有定量研究。
考慮到前期研究主要圍繞矩形裂縫[16],所以筆者以儲熱圓棒混凝土為例,對比研究存在弧狀裂縫和弦狀裂縫時的混凝土放熱特性,并從裂縫的圓心角、寬度和位置進行數值分析,給出裂縫溫差(放熱過程中某時刻裂縫中的最大溫差)在放熱過程中的變化曲線。利用擬合函數確定裂縫溫差峰值與裂縫參數的關系,從定量角度分析混凝土在熱應力極限情況下裂縫參數的安全范圍,為預防和控制混凝土裂縫的研究提供參考。
1 計算模型
1.1 數值模型
圖1為所研究對象的數值模型均以裂縫的內邊界作為裂縫特征位置,其中:φ為裂縫圓心角,(°);δ為裂縫寬度,mm;x為裂縫位置特征長度,mm。
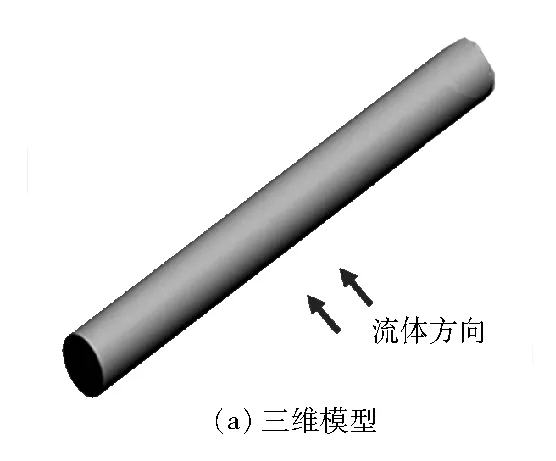
圖1 數值模型
傳熱介質為導熱油,橫掠混凝土圓棒進行熱交換。由于混凝土的導熱系數低,可忽略其軸向溫度變化,將三維模型簡化成二維模型。研究在放熱條件下,不同圓心角、寬度和位置的裂縫對混凝土內部溫度分布的影響,以及裂縫處溫差變化對混凝土熱應力的影響。從儲熱模塊到外部環境沒有熱損失,因為模塊通常采用良好的隔熱。
1.2 計算條件
假定放熱過程中各工質的物性參數為常數,材料物性參數見表1[17],在典型工況下進行數值模擬。混凝土初始溫度為390 ℃,導熱油的進口溫度為290 ℃、流速為0.004 m/s,經計算可得對流傳熱系數為32.97 W/(m2·K)。在低溫導熱油冷卻高溫混凝土的過程中,混凝土的溫度隨時間不斷變化,屬于非穩態傳熱過程,所以選用瞬態熱分析法進行計算,時間設置為2 000 s。
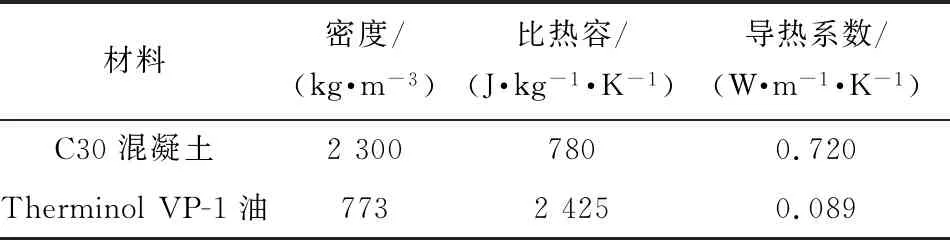
表1 材料物性參數
2 理論分析
2.1 傳熱機理
混凝土放熱過程中,包含導熱、對流和輻射。根據劉光鵬等[16]的研究結果,在混凝土裂縫中,對流傳熱量、輻射傳熱量遠低于導熱傳熱量,因此在研究中以導熱為主。將非穩態導熱微分方程應用于該問題,方程為:
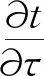
(1)
式中:t為溫度,℃;τ為時間,s;a為熱擴散系數,m2/s。
2.2 熱應力的理論計算
理想條件下混凝土無裂縫,內部溫度均勻變化時,熱應力可處于穩定的安全值。但是,由于在原混凝土制造過程中,內部冷卻不易均勻,儲熱混凝土中,必定存在裂縫。高溫放熱過程中,混凝土內部溫度梯度大,裂縫處的溫差由于空氣熱阻的存在而明顯高于其他部位,因此裂縫處由溫差引起的熱應力也將更大。當裂縫局部的熱應力大于混凝土的極限熱應力時,混凝土會在裂縫處二次開裂,降低傳熱效果,甚至危害設備運行安全。
根據混凝土結構的二維溫度應力的計算過程,最大溫度應力σmax[18]為:
(2)
式中:H(τ)為與時間有關的應力松弛系數,取0.327;α為線膨脹系數,K-1;Δt為裂縫溫差,K;μ為泊松比,取1.5;kr為約束程度函數,采用完全約束時為1;C為阻力系數;E為彈性模量,Pa;L為圓棒長度,m;B為圓棒直徑,m。
選取C30混凝土作為研究對象,混凝土圓棒的直徑為80 mm,線膨脹系數為1×10-5K-1,彈性模量為3.0×104MPa。根據GB 50010—2010《混凝土結構設計規范》查得,混凝土30 d齡期的抗拉強度為2.01 MPa。
裂縫溫差決定混凝土裂縫處的熱應力,而熱應力是決定高溫儲熱混凝土是否會二次開裂的直接因素。當混凝土內部最大裂縫溫差為24.105 K時,內部熱應力達到2.01 MPa,此時混凝土進一步開裂。但不同圓心角、位置和寬度的裂縫對于混凝土熱應力的影響尚不清晰,需要對其進行數值模擬計算,得出混凝土的溫度分布,這有助于對儲熱模塊放熱性能進行優化。
3 結果與分析
3.1 裂縫圓心角的影響
從具有計算意義的小圓心角(5°)開始選取10個圓心角,設置裂縫的寬度為2 mm、位置特征長度為20 mm進行模擬,以期得到裂縫圓心角對于混凝土溫度分布的影響。圖2為圓棒混凝土放熱2 000 s的溫度分布。



圖2 混凝土放熱2 000 s的溫度分布
由圖2可得:無裂縫時,圓棒混凝土中心溫度最高,沿半徑方向逐漸降低;存在裂縫時,混凝土仍以導熱方式向外發散熱量,但由于裂縫內空氣熱阻的存在,熱量傳遞的路徑發生變化,高溫中心向裂縫移動,更多的熱量直接由內部的混凝土傳遞給流體,不經過裂縫;相比于裂縫外邊界,內邊界的導熱路徑更長、熱阻更大,因此內邊界溫度高于外邊界溫度。
圖3為不同圓心角時圓棒混凝土的裂縫溫差隨時間的變化。
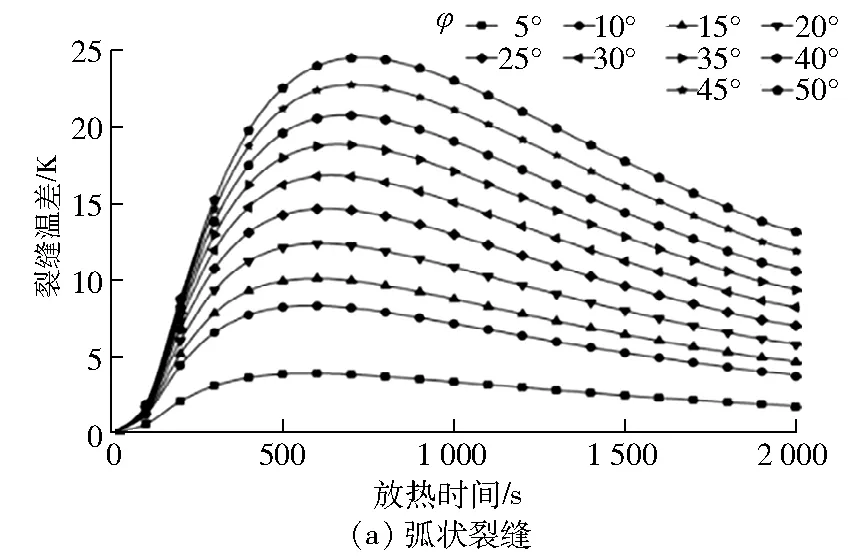
圖3 不同圓心角時裂縫溫差隨時間的變化
由圖3可得:隨著放熱的進行,兩類裂縫處的溫差均先呈現快速增長,到達峰值后逐漸緩慢降低。這是由于裂縫中空氣熱阻遠大于混凝土導熱熱阻,熱量大多直接通過混凝土傳導至外界。與內邊界相比,裂縫外邊界向外界導熱路徑更短,熱量快速散失后穩定在低溫;內邊界由于有更長的導熱路徑,熱量散失緩慢并且穩定。當圓心角變大時,弧狀裂縫的弧度變長,裂縫溫差呈現遞增趨勢。圓心角從5°到10°時,裂縫溫差整體增加了5 K左右,增加較大;圓心角為10°~50°時,各區間裂縫溫差變化僅約為2 K。在放熱過程中,弧狀裂縫和弦狀裂縫的溫差變化趨勢一致,但弧狀裂縫溫差略大于弦狀裂縫溫差,原因是對于相同的圓心角,弧狀裂縫兩側的傳導路徑差值比弦狀裂縫的更大。
3.2 裂縫寬度的影響
選取裂縫的圓心角為35°、特征位置長度為20 mm,研究裂縫寬度對裂縫溫差的影響。圖4為不同裂縫寬度時裂縫溫差隨時間的變化。由圖4可得:隨著放熱時間的增加,裂縫溫差全部呈現先快速增加至峰值而后緩慢降低的趨勢。這與圖3曲線的趨勢一致,其原因也相同。
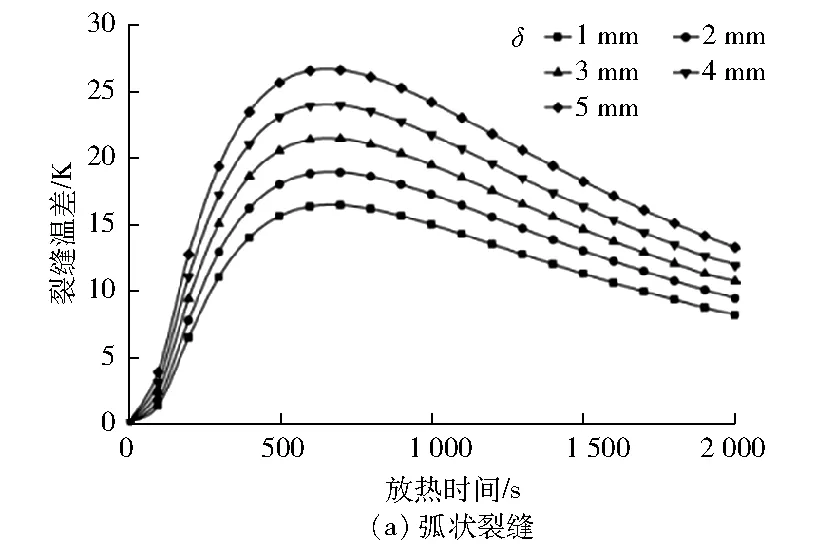
圖4 不同裂紋寬度時裂縫溫差隨時間的變化
3.3 裂縫位置的影響
選取裂縫的圓心角為35°、寬度為2 mm,研究裂縫位置對裂縫溫差的影響。圖5為不同裂縫位置特征長度時裂縫溫差隨時間的變化。

圖5 不同裂縫位置特征長度時裂縫溫差隨時間的變化
由圖5可得:針對弧狀裂縫,當裂縫位置特征長度≤5 mm時,裂縫溫差基本沒有變化,是因為裂縫足夠靠近儲熱圓棒中心,熱量沿半徑方向從裂縫內外邊界向儲熱棒表面傳遞的路徑長度相差不大;當裂縫位置特征長度>5 mm時,裂縫溫差波動明顯。隨著放熱的進行,裂縫溫差均呈現先增加后下降的趨勢,并且裂縫位置特征長度越大,裂紋溫差增加的幅度越大,主要原因是裂縫中存在空氣熱阻,會阻礙混凝土連續地導熱,更多的熱量將改變導熱路徑,避開裂縫,通過混凝土沿半徑方向向表面傳遞。裂縫內邊界的導熱路徑較長,放熱緩慢;裂縫外邊界的導熱路徑較短,放熱迅速。這會導致放熱過程中裂縫溫差分布差異明顯。當圓心角不變時,裂縫距離儲熱圓棒中心越遠,意味著弧狀裂縫的弧長更大,由于位置和弧長的疊加效果,裂縫兩側導熱的不均勻性增大,所以裂縫距離儲熱圓棒中心越遠,裂縫溫差及其增加幅度越大。與弧狀裂縫相比,弦狀裂縫在放熱過程中的裂縫溫差整體更小,是因為弦狀裂縫兩側導熱路徑的差距比弧狀裂縫的小。
3.4 裂縫參數與熱應力的關系
為進一步研究裂縫參數對混凝土熱應力的影響,模擬得到裂縫參數對裂縫溫差峰值的影響(見圖6)。由圖6可得:圓心角、裂縫寬度和裂縫位置特征長度對裂縫溫差峰值的影響均呈正相關性,但在不同參數條件下,弧狀裂縫的裂縫溫差峰值均大于弦狀裂縫的裂縫溫差峰值。裂縫溫差對熱應力有直接影響,當裂縫處的熱應力超過極限會導致混凝土再次開裂,降低混凝土圓棒的熱性能,并且影響其正常使用。為探究裂縫參數與裂縫溫差的函數關系,進而定量分析混凝土極限熱應力對應的安全裂縫參數范圍,在數值模擬的基礎上擬合出裂縫的圓心角、寬度和位置特征長度與裂縫溫差峰值Δtmax的函數關系式。
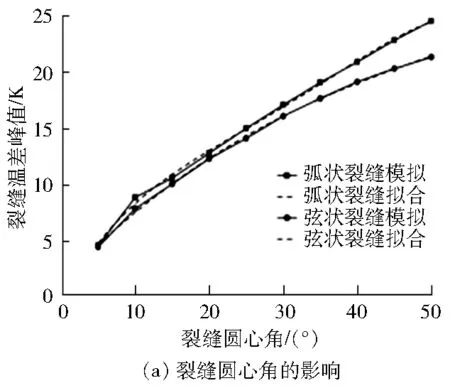
圖6 不同參數對裂縫溫差峰值的影響
(1)裂縫圓心角與裂縫溫差峰值的關系式。
弧狀裂縫Δtmax為:
Δtmax=9.9×10-5φ3-0.011φ2+
0.776φ+0.72
(3)
弦狀裂縫Δtmax為:
Δtmax=4.306φ3-0.008φ2+
0.709φ+0.625
(4)
(2)裂縫寬度與裂縫溫差峰值的關系式。
弧狀裂縫Δtmax為:
Δtmax=2.546δ+13.818
(5)
弦狀裂縫Δtmax為:
Δtmax=2.368δ+12.824
(6)
(3)裂縫位置特征長度與裂縫溫差峰值的關系式。
弧狀裂縫Δtmax為:
Δtmax=0.002 44x3-0.08x2+
1.797x-5.47
(7)
弦狀裂縫Δtmax為:
Δtmax=0.001 77x3-0.05x2+
1.389x-4.32
(8)
所選用的混凝土的極限裂縫溫差為24.105 K,通過計算得到該案例裂縫參數的安全范圍(見表2)。

表2 裂縫參數的安全范圍
4 結語
通過理論分析和數值模擬研究裂縫的圓心角、寬度和位置與溫差的關系,并給出了溫差和熱應力的函數關系,定量分析了影響混凝土進一步開裂的因素,得到的主要結論為:
(1)隨放熱的進行,裂縫溫差呈現先增大后遞減的趨勢,且隨著裂縫的圓心角、寬度和位置特征長度的增大,變化得更劇烈。
(2)混凝土放熱過程中,裂縫溫差整體上與裂縫的圓心角、寬度及位置呈正相關性;但是,當裂縫位置特征長度≤5 mm時,裂縫溫差基本無變化。
(3)相同裂縫參數條件下,弧狀裂縫與弦狀裂縫的裂縫溫差的變化趨勢基本一致,但弦狀裂縫的裂縫溫差峰值略低于弧狀裂縫的裂縫溫差峰值。
(4)針對該混凝土圓棒,通過公式擬合和定量分析得到:對于弧狀裂縫,不開裂的要求是圓心角為0°~48.67°,寬度為0~4.04 mm,裂縫位置特征長度為0~23.43 mm;對于弦狀裂縫,不開裂的要求是圓心角為0°~62.98°,寬度為0~4.76 mm,裂縫位置特征長度為0~24.29 mm。

