超超臨界機組全負荷段機爐協調系統建模研究
高 崢,呂劍虹,屈小凡,葛 浩
(東南大學 能源與環境學院,南京 210096)
隨著電網清潔能源增加,以及全社會用電需求增速放緩,使得電網峰谷差越來越大,在保證清潔能源不棄風棄光的情況下火電機組調峰任務越來越突出。因此,提升火電機組運行靈活性,使其大規模參與電網深度調峰將是大勢所趨。
國內外在協調系統建模方面的研究有很多,LIU J Z等[1-2]在文獻[3]的基礎上,通過合理簡化和機制分析,根據質量、能量和動量平衡方程建立適用于直流爐機組協調控制系統控制器設計的簡化非線性數學模型,該模型結構簡單,具有一定的實用性。陳寶林等[4]利用最小二乘法建立了協調系統的模型,該模型在某個負荷點上的模擬結果精確,但不適用于大范圍工況變化的情況,運用神經網絡模型進行改進,模擬結果的精度明顯提高。韋根原等[5-6]運用粒子群算法分別建立了350 MW超臨界機組和1 000 MW超超臨界機組的傳遞函數模型,提高了辨識的精確性與快速性。
深度調峰負荷變化范圍較廣,目前的建模研究大多集中在干態情況下,為了進一步了解濕態下的機組運行動態特性,同時在模型基礎上研究深度調峰下的新型協調控制方法,需要建立能夠正確反映機組中各設備參數的變化,以及機組動態響應的全負荷段非線性模型。筆者以國內某1 000 MW超超臨界機組為研究對象,由于鍋爐和汽輪機中汽水系統復雜,對工質采用移動邊界建模實施難度大,所以采用分段集總參數法建立非線性模型,采用教與學算法計算模型中的參數,通過與現場實際數據仿真驗證,證明了該模型具有一定應用價值。
1 全負荷段非線性模型
1.1 模型結構及假設
超超臨界機組的協調系統主要包括鍋爐燃燒系統、汽水系統和汽輪機系統三部分。鍋爐燃燒系統為煤通過磨煤機制粉后進入鍋爐燃燒,汽水系統包括省煤器、水冷壁、過熱器和再熱器。給水先后進入省煤器、水冷壁加熱后經汽水分離器將蒸汽分離,分離出的蒸汽進入過熱器進一步加熱,產生的高溫高壓蒸汽進入汽輪機系統高壓缸做功,高壓缸排汽經過再熱器加熱后進入中低壓缸做功。
對于超超臨界機組的協調系統建模,一般輸入量為給水流量、給煤量和汽輪機調節閥開度,需要求解中間點溫度(汽水分離器出口蒸汽溫度)、主蒸汽壓力、主蒸汽溫度和機組功率。往常的干態模型若應用于全工況下濕態模型有較大的誤差,誤差來源為:(1)機組在低負荷段時,汽水分離器出口帶水,機組進入濕態,汽水分離器中一部分流量經過再循環回到水冷壁,在干態下的質量平衡方程將不準確;(2)水冷壁和過熱器由于吸熱特性不同,吸熱量比例發生變化,從而導致汽水分離器出口參數發生變化;(3)當機組在低負荷段時進入濕態,汽水分離器儲水罐的水位也應作為輸出量。因此,需要建立適合干態和濕態的全負荷段模型。筆者首先對真實系統進行適當簡化:鍋爐段模型將省煤器和水冷壁簡化為一根均勻受熱的管道,吸熱量為Q1;將過熱器單獨簡化為一根均勻受熱的管道,吸熱量為Q2。簡化后鍋爐模型結構見圖1。
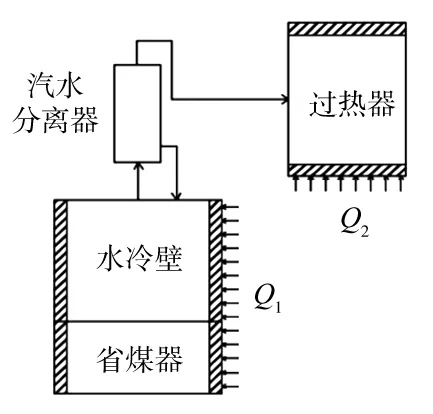
圖1 鍋爐段簡化模型
對簡化后的鍋爐模型進行以下假設:
(1)假定省煤器-水冷壁、過熱器的金屬溫度與工質溫度相同,且金屬溫度與工質溫度同步變化。
(2)將汽水分離器和儲水罐簡化為一個圓柱形容器。
(3)忽略汽水分離器內工質旋流對能量損失的影響。
(4)忽略汽水分離器散熱對能量損失的影響。
(5)假定汽水分離器內部工質分布均勻且分離效率為1。
由此簡化后的協調系統可分為鍋爐部分和汽輪機部分,鍋爐部分又分為鍋爐燃燒過程、省煤器-水冷壁吸熱過程、過熱器吸熱過程3個過程以及汽水分離器1個中間環節,采用出口參數作為集總參數。
1.2 全負荷段模型建立
1.2.1 鍋爐部分
(1)鍋爐燃燒過程。
鍋爐燃燒過程采用文獻[7]中所建模型的制粉過程和燃燒放熱,計算公式為:
(1)
Qb=μbqm,b
(2)
式中:qm為給煤質量流量,kg/s;qm,b為煤粉質量流量,kg/s;s為復參數,t0為慣性時間,s;τ為純延遲時間,s;Qb為鍋爐總放熱量,kJ/s;μb為煤燃燒熱值,kJ/kg。
(2)省煤器-水冷壁吸熱過程。
為進一步簡化模型,假設:忽略煙氣側的動態過程;煙氣側向管側傳熱是強制傳熱;忽略管長方向的軸向傳熱。考慮管內工質的密度變化帶來的流量變化,以及金屬的蓄熱量,則工質的質量平衡方程和能量平衡方程為:
(3)
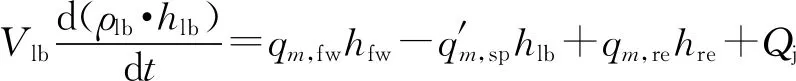
(4)
式中:t為時間,s;Vlb為省煤器-水冷壁管內體積,m3;ρlb為省煤器-水冷壁出口工質密度,kg/m3;qm,fw為給水質量流量,kg/s;q′m,sp為汽水分離器進口工質質量流量,kg/s;qm,re為再循環水質量流量;kg/s;hlb、hfw和hre分別為省煤器-水冷壁出口工質焓、給水焓和再循環水焓,kJ/kg;Qj為省煤器和水冷壁的金屬吸熱量,kJ/s。
而省煤器-水冷壁的金屬吸熱量的一部分傳遞給管內工質,另一部分用于自身蓄熱,因此其能量平衡方程為:
(5)
(6)
式中:k為傳熱系數,W/(cm2·K);Qlb為省煤器-水冷壁吸熱量,kJ/s;Tj為省煤器-水冷壁的金屬壁溫,℃;cj為金屬比熱容,kJ/(kg·K);mj為省煤器-水冷壁的金屬質量,kg。
由于省煤器-水冷壁出口工質焓hlb即為汽水分離器進口工質焓hsp,將其作為狀態變量,對式(3)和式(4)整理可得:
(7)
qm,fwhfw-q′m,sphlb+qm,rehre+Qj
(8)
令a1=2Vlb(?ρlb/?hsp),a2=2Vlbρlb,將式(7)代入式(8)并將式(6)代入式(5)可得省煤器-水冷壁部分模型:
(9)
省煤器-水冷壁出口工質密度ρlb等于汽水分離器進口工質密度ρsp,a1為待辨識的動態參數。
(3)汽水分離器環節。
對汽水分離器建模主要是為了在機組進入濕態時得到再循環水流量和汽水分離器儲水罐水位,因此對汽水分離器列出質量和能量平衡方程。
質量平衡方程為:
(10)
式中:Vsp為汽水分離器中工質體積,m3;q″m,sp為汽水分離器出口蒸汽質量流量,kg/s。
由汽水分離器儲水罐水位H和汽水分離器截面積F可得:
Vsp=Vw+Vi=HF+Vi
(11)
式中:Vw和Vi分別為汽水分離器中水和蒸汽的體積,m3。參照式(8)單獨對Vw部分列質量平衡方程可得汽水分離器儲水罐水位變動方程為:
(12)
式中:ρw為飽和水密度,kg/m3;x′為汽水分離器進口工質干度。
能量平衡方程為:
q′m,sph′sp-q″m,sph″sp-qm,rehre
(13)
式中:hw為飽和水焓,kJ/kg;ρi為飽和蒸汽密度,kJ/kg;hi為飽和蒸汽焓,kJ/kg。
式(13)對汽水分離器出口壓力psp求偏導并代入式(12)可得:
(14)
令b1=?ρihi/?psp,b2=?ρwhw/?psp,b3=?Tj/?psp,b1、b2、b3為待辨識的動態參數,式中ρw、ρi、hi和hw均可由psp得出,因此令g=(ρihi-ρwhw)/ρw=f(psp,hsp),整理后汽水分離器模型為:
(15)
W=g(q′m,sp-q″m,sp-qm,re)
(4)過熱器吸熱過程。
主要研究協調系統部分的建模,故不考慮過熱減溫水的影響,由汽水分離器模型可得汽水分離器出口蒸汽壓力,可根據動量方程得到主蒸汽壓力:
(16)
式中:qm,st為主蒸汽質量流量,kg/s;pst為主蒸汽壓力,MPa;λst為流動阻力系數;ρst為主蒸汽密度,kg/m3。由文獻[7]可將式(16)簡化為:
qm,st=k3(psp-pst)
(17)
式中:k3為待辨識參數。質量平衡方程和能量平衡方程與省煤器-水冷壁模型相似,以過熱器出口參數為集總參數,進入過熱器蒸汽質量流量為汽水分離器出口蒸汽質量流量q″m,sp,進入汽輪機蒸汽質量流量為主蒸汽質量流量qm,st,可得過熱器段的質量平衡方程為:
(18)
式中:Vgr為過熱器段管內體積,m3。
過熱器段吸熱量Qg由省煤器-水冷壁吸熱比例klb可得,即Qg=(1-klb)Qb,因此過熱器段能量平衡方程為:
(19)
式中:mg為過熱器段金屬質量,kg;Tg為過熱器段金屬壁溫,℃。參考省煤器-水冷壁部分模型可得過熱器部分模型:
(20)
式中:Tst為主蒸汽溫度,℃。
1.2.2 汽輪機部分
對汽輪機部分,將汽輪機入口處的蒸汽流量和壓力、溫度的關系表示為:
qm,st=g(ut)f(pst,Tst)
(21)
式中:ut為汽輪機調節閥開度,%;g(·)、f(·)分別表示一種函數關系。文獻[4]提出函數關系可以表示為:
(22)
式中:ttur為慣性時間,s,一般取10~20 s。在式(22)的基礎上辨識函數k(ut),假設k(ut)為多項式形式:
(23)
機組發電功率Ne可由能量平衡[2]計算得出:
Ne=k2qm,st(hst-hfw)
(24)
式中:k2為考慮機組發電效率的等效系數。
2 模型參數求取
2.1 靜態參數計算
由上述建模結果可知,待辨識的參數有a1、b1、b2、b3、c1、c2、klb、k、k2和k3,共10個,klb和k2可根據表1數據靜態辨識,另外制粉過程的時間常數t0和τ可以參考同類型磨煤機的取值[7]。
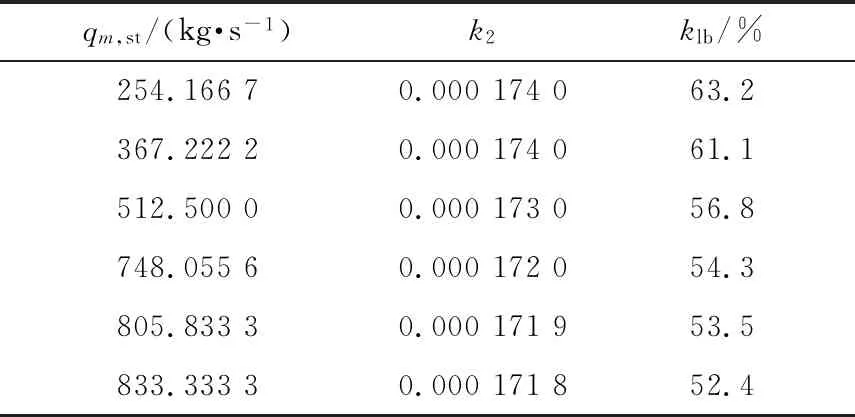
表1 模型靜態參數
表1中qm,st和klb由國內某1 000 MW機組現場歷史運行數據得到,因為省煤器-水冷壁金屬質量與包括頂棚過熱器、包覆過熱器、一級過熱器和二級過熱器的過熱器部分金屬質量相近,因此可以近似認為省煤器-水冷壁吸熱比例為工質在省煤器-水冷壁的吸熱量與工質總焓升之比[8]。由表1可見:k2在隨qm,st變化時變化不大,故取k2=0.001 73。klb經過測試采用有理函數逼近效果最佳,有理函數可寫為:
(25)
式中:P(x)和Q(x)均為(ax-b)n的多項式,a和b為待擬合系數。利用MATLAB軟件擬合工具箱擬合一次有理函數得到:
klb=(9.63qm,st+195 200)/(0.278qm,st+2 665)
(26)
2.2 動態參數計算
2.2.1 教與學算法
動態參數部分利用機組實際運行數據,通過教與學算法辨識。教與學算法與粒子群算法、遺傳算法等同屬于一種群智能優化算法,與其他群智能算法不同的是教與學算法不需要設置算法自身的計算參數,且簡單易實現。
教與學算法中學生成績Xi被當作種群中的第i個個體,學生各個科目的成績作為待優化的解,科目的多少為待優化解的維度,最好的成績作為老師成績Tj,分為“教”和“學”兩個階段。
在教階段,學生向老師學習,假設在第j次循環中,學生根據所有學生的平均成績Pj與老師成績之間的差距Dj進行學習,其中:
Dj=rj(Tj-R·Pj)
(27)
式中:rj為1到2之間的隨機數;R代表學習作用的強弱,一般取1或2。此時學生根據平均成績更新自身成績:
Xi,j=Xi,j-1+Dj
(28)
若成績優于更新前則接受更新,否則不更新。
在學階段,學生之間相互學習,假設在第j次循環中,隨機抽取一個學院成績Xk,j進行學習:
Xi,j=Xi,j-1+n·rj(Xi,j-Xk,j)
(29)
式中:n為學習判斷系數。如果Xk,j成績優于Xi,j,則n=1,否則n=-1。同樣檢驗更新后的成績是否優于更新前,若優于更新前則接受更新,否則不更新。
2.2.2 參數計算
由于教與學算法本身基不需要參數設置,只需要對待辨識參數設置搜索范圍,共有a1、b1、b2、b3、c1、c2、k和k38個參數需要辨識,搜索范圍見表2。
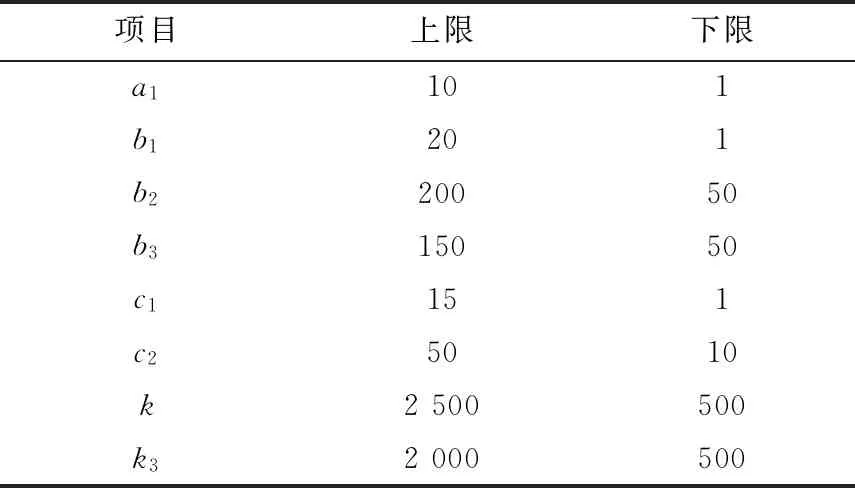
表2 待辨識參數搜索范圍
算法適應度函數為:
(30)
式中:t1為仿真結束時間;Δ為模型計算值與現場實際值的差;下標0為現場實際值。F(x)越小表明模型與實際過程越接近,當算法達到迭代上限或已收斂,則停止迭代,得到最終的模型參數。
設置教與學算法種群數量為50,迭代上限為50次,利用國內某1 000 MW機組現場運行數據,輸入給煤量、給水量、再循環水流量和汽輪機調節閥開度,得到計算結果見表3。
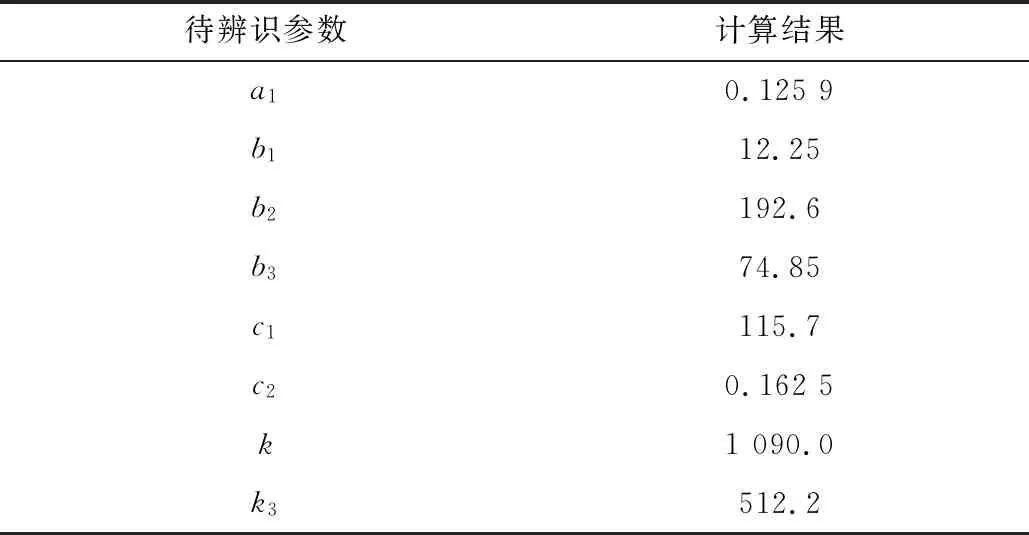
表3 待辨識參數計算結果
3 模型驗證
利用現場機組降負荷時干態轉濕態過程的數據對模型進行驗證,0 s時機組實發功率為338 MW,給煤質量流量為120 t/h,進入省煤器的給水質量流量為1 066 t/h,主蒸汽壓力為9.8 MPa。當實發功率為319 MW時機組由干態開始進入濕態。對比模型輸入給煤量、給水量、再循環水流量和汽輪機調節閥開度,得到模型對比驗證曲線見圖2。
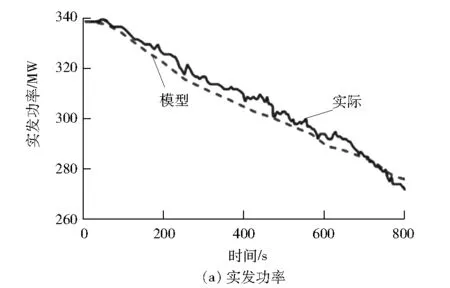
圖2 干態轉濕態模型對比驗證曲線
由圖2可得:模型對機組實發功率和主蒸汽壓力的模擬比較準確;在儲水罐水位方面,干態過程時,模擬值與實際值誤差較小,而濕態過程在250 s開始水位有較大幅度上升,在610 s開始下降至穩定,這是因為再循環水流量增加使得模型輸出水位出現較大變化,其中模型計算的水位變化速率較快,變化幅度較大,這是由于儲水罐容積計算與實際存在偏差,慣性容積不同導致水位變化速率有差異;在汽水分離器出口焓方面,在干態和濕態的起始過程,模擬值和實際值的計算誤差較小,在430 s后有一定偏差,其原因一方面是模型計算簡化,忽略了散熱等能量損失,另一方面是汽水分離器干度存在計算誤差或分布不均,在功率變化過程中給水對主蒸汽壓力的作用較快導致在濕態下模擬值與實際值有偏差。但總體上該模型可以正確反映機組變化狀態并滿足仿真的要求。
利用模型仿真機組濕態轉干態的過程,0 s時機組實發功率為388 MW,給煤質量流量為176 t/h,進入省煤器的給水質量流量為1 100 t/h,主蒸汽壓力為11.46 MPa,得到模型對比驗證曲線見圖3。
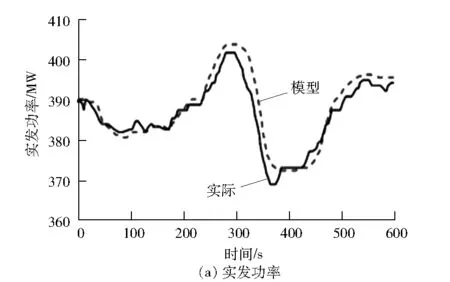
圖3 濕態轉干態模型對比驗證曲線
從圖3可以看出:濕態轉干態過程的煤量變化與干態轉濕態時相比變化較大,導致主蒸汽壓力和實發功率發生振蕩,主蒸汽壓力最大偏差為0.06 MPa,實發功率最大偏差為5.4 MW,在整個振蕩過程中模型輸出與實際情況趨勢基本一致,總體上模型輸出比較準確。儲水罐的實際水位與模型計算結果趨勢一致,但模型的水位速率變化較快,理論分析水位在干態中應變為0 m水位,而實際水位在干態中仍留有一點水位,是由于水位已處于測量下限以下。在濕態轉干態過程中,實際汽水分離器出口焓先下降后再上升,其原因可能是調節過程中實際水對主蒸汽壓力的作用比煤快,實際汽水分離器熱容與模型計算有偏差導致,在濕態轉干態過程有一定幅度的下降。
結合圖2和圖3可得:該模型在干態過程比較準確,在濕態過程時有一定誤差,但整體趨勢是一致的,可以反映機組的運行狀態,滿足仿真的要求。
4 結語
隨著對超超臨界機組的深度調峰要求越來越高,在對超超臨界模型的研究中,往常的干態模型應用于全工況下濕態模型有較大的誤差,由于汽水分離器出口帶水導致干態計算公式不再適用于濕態,需要重新建模。筆者提出的全工況協調系統模型,利用質量和能量平衡建立了省煤器-水冷壁、汽水分離器、過熱器和汽輪機的非線性模型,針對模型中無法確定的參數,通過理論與經驗相互結合的方式,基于歷史數據,采用教與學的啟發式算法進行確定。最后進行干態轉濕態和濕態轉干態過程的仿實驗,仿真結果表明模型在干態和濕態能夠較好地反映機組的特性,其中干態過程更為準確,濕態過程有一定誤差。

