無砟道床層間植筋錨固連接的力學模型研究

張曉東,岳 彤

(1.石家莊鐵道大學土木工程學院,石家莊 050043； 2.中國鐵路設計集團有限公司,天津 300308)

鐵路無砟軌道是一種多層復合結構體系。保證服役期無砟道床層間變形協調關系符合設計要求，對保持無砟軌道良好的服役性能至關重要[1]。植筋錨固是無砟軌道設計和維修養護中最常用的一種加強層間連接的方式[2-3]。CRTSⅡ型板式無砟軌道設計時在梁縫區域、過渡段等特殊位置將軌道板與底座板或支承層用植筋進行錨固連接，運營中出現層間離縫、接縫破損或軌道板高溫上拱等病害時使用植筋錨固方法進行整治；CRTSⅠ、CRTSⅢ型板式無砟軌道使用植筋錨固方法進行軌道板翹曲變形整治；隧道內雙塊式、彈性支承塊式無砟軌道在洞口段及伸縮縫前后道床板與仰拱回填層或底板設置植筋錨固。

植筋錨固就是以專用的結構膠粘劑將帶肋鋼筋或全螺紋螺桿種植于無砟軌道混凝土結構層中的后錨固連接方法之一，它可以起到限制層間相對滑移和脫離的作用。合理的植筋方案設計是保證錨固效果，節約工程費用的關鍵。植筋錨固連接力學模型是植筋方案設計分析計算的基礎。目前，在無砟軌道設計和病害整治的分析計算中，對植筋錨固連接的處理有多種方式。文獻[4-5]進行實驗室實尺模型獲得植筋錨固結構的荷載-位移曲線；文獻[6-7]在CRTSⅡ型板式無砟軌道不同植筋錨固方案研究中，用非線性彈簧模擬植筋錨固連接，其剛度采用實驗實測的錨栓的荷載-位移曲線；文獻[8]采用線性彈簧模擬植筋錨固連接，主要根據錨栓的彈性模量對彈簧單元的參數進行定義；文獻[9-11]在無砟軌道整體模型中依據植筋錨固的構造建立細化模型。

上述處理方法各有其優勢和不足。實測植筋錨固結構荷載-位移曲線的方法結果真實可靠，但試件的制作、試驗等工作量很大，耗時長，費用高，一般只可能做有限的工況。用錨栓荷載-位移曲線代替植筋錨固連接的力學參數，實驗相對簡單，但沒有考慮植筋膠的作用，誤差較大。在整體模型中建立植筋錨固的細化模型，由于需要考慮建模工作量和計算代價，一般不能考慮植筋膠，模型的精細程度不高，導致計算結果精度不足，可靠性不高，計算工作量也較大。可見，目前無砟道床層間植筋錨固連接還沒有公認、統一的力學模型，也缺乏相關專門的研究。這給無砟軌道設計、維修中植筋錨固方案的優化計算帶來了困難。本文基于多尺度建模技術的理念，在宏觀尺度上將植筋抽象為三向非線性軸向彈簧，通過建立細觀尺度的植筋錨固連接的精細化模型，對植筋連接的力學性能進行研究，獲取各向非線性彈簧參數，用于整體建模中替代植筋錨固連接。這種分步、多尺度建模方法，既避免了試驗的時間和資金成本，又保證了計算的高效和準確。

1 植筋錨固連接的受力及力學模型

1.1 植筋錨固連接的受力分析

植筋錨固連接主要用于限制無砟道床層間相對滑移和脫離。在分塊布置的無砟軌道設計時，為限制由于整體溫升或溫降造成軌道結構層產生伸縮位移[12-13]，底座板與下部結構間設置植筋錨固[10]；為整治縱連板式無砟軌道在較大溫度力作用下導致的軌道層間剪切破壞而形成大范圍離縫及較大縱向位移[14-16]，在軌道板與底座板之間設置植筋錨固[6-7]。上述情況下設置的植筋錨固主要約束層間縱向或橫向的相對滑移，植筋錨固連接起抗剪作用，主要承受剪力。在整治縱連板式無砟軌道板整體高溫上拱時，利用植筋錨固將軌道板與底座板連接到一起[8-9，11]；在整治由于溫度梯度造成的單元板溫度翹曲時，在軌道板板端設置植筋錨固[17-20]。上述情況下設置的植筋錨固主要限制層間的脫離，植筋錨固連接起抗拔作用，主要承受拉力。實際中，植筋錨固連接在大多數情況下同時起抗拔和抗剪作用，同時承受拉力和剪力[10]。

由于化學粘結錨栓的破壞面一般發生在混凝土和植筋膠的表面，因此，植筋錨固的抗拔能力主要由錨栓與混凝土之間的黏結力產生，包括植筋膠與錨栓表面的化學膠著力、植筋膠與混凝土接觸面的化學膠著力，以及植筋膠與混凝土接觸面的機械咬合力，主要由錨栓承擔。如圖1所示。

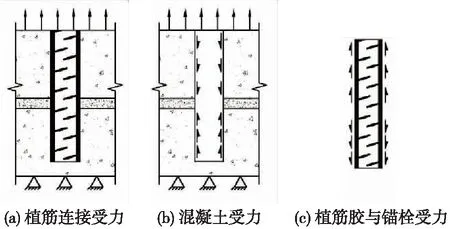
圖1 抗拔力作用示意

植筋錨固的抗剪能力主要由兩個基材的分層界面的機械咬合力和錨栓的抗剪切力提供。如圖2所示。

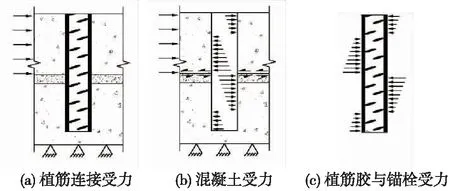
圖2 抗剪力作用示意

1.2 植筋錨固連接的力學模型

植筋錨固連接的抗拔和抗剪力學性能用其荷載-位移曲線表征，類似于彈簧在不同作用力下產生不同變形的受力性能。因此，在軌道結構整體建模時，可以將植筋錨固連接的抗拔和抗剪力學性能等效為彈簧。其縱向、橫向抗剪能力和豎向抗拔能力，分別等效為3個非線性軸向彈簧，如圖3所示。植筋錨固連接的荷載-滑移曲線用彈簧的荷載-位移特性曲線(F-D曲線)表征。

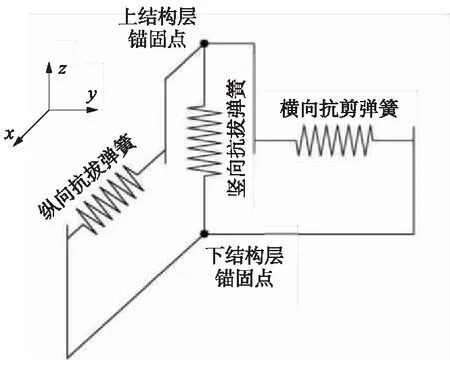
圖3 植筋錨固連接等效力學模型示意

2 植筋錨固連接的小尺度有限元模型

獲得植筋錨固連接荷載-滑移曲線的最可靠途徑是實尺實驗。但試件的制作及試驗工作量很大，耗時長費用高。基于多尺度建模技術的理念，可以先建立細觀尺度的植筋錨固連接的精細化有限元模型，對植筋連接的力學性能進行研究，獲取植筋錨固連接的荷載-滑移曲線，再用于無砟軌道整體建模中等效植筋錨固連接。這種分步、多尺度建模方法，既縮減了試驗的時間和資金成本，又保證了計算的高效性和準確性。

植筋錨固連接中有3種不同的介質，即混凝土、錨栓和植筋膠。要建立植筋錨固連接的精細化有限元模型，需重點考慮3方面問題：不同介質在尺度上較大的差異性，特別是植筋膠的厚度僅為2～4 mm；各種材料本構關系的非線性特征；混凝土與植筋膠、鋼筋與植筋膠之間的界面性能。

2.1 材料本構關系

錨栓為鋼材，采用雙線性理想彈塑性應力-應變本構關系曲線，按式(1)確定。

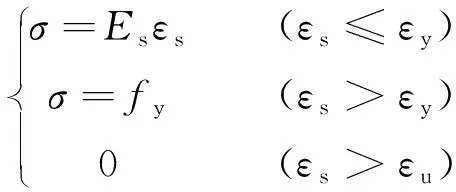
(1)

式中，Es為鋼筋彈性模量；εs為鋼筋的應變，fy，εy分別為鋼筋的屈服強度及屈服應力對應的屈服應變，εy=fy/Es；εu為對應鋼筋極限強度的峰值應變。

軌道板、底座板混凝土的受拉、受壓應力-應變本構關系曲線分別按式(2)、式(3)確定

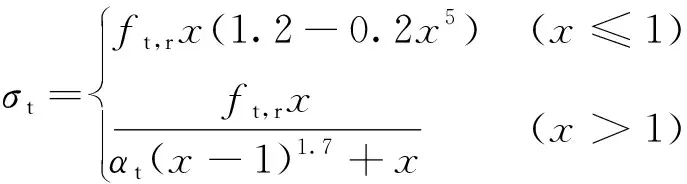
(2)

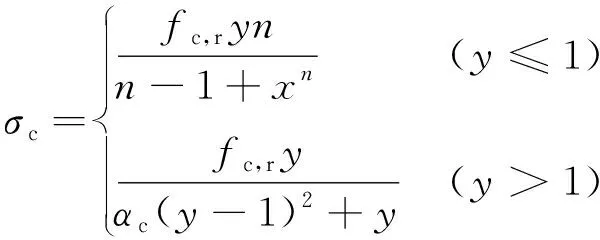
(3)

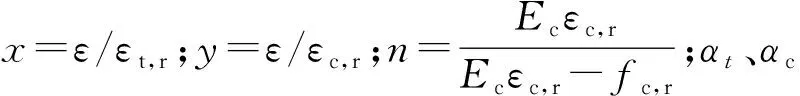
植筋膠是錨栓與基材混凝土連接的關鍵介質，其雖然僅有幾毫米的厚度，但其力學性能對植筋錨固連接的力學特性影響很大，其本構關系是植筋錨固連接問題有限元分析的關鍵。植筋用化學粘結劑一般為改性環氧樹脂類或改性乙烯基酯類材料，實驗表明[21]，植筋膠的材料性能類似于混凝土，故采用類似于混凝土的本構關系。

2.2 粘結界面模型

錨固連接可能的破壞形式有基材混凝土破壞、錨栓破壞、植筋膠破壞、混凝土與植筋膠之間的粘結破壞、鋼筋與植筋膠之間的粘結破壞等5種形式，但大多數情況下破壞發生在膠筋、膠混界面[22-23]。因此，粘結界面模型對分析植筋錨固受力特性十分重要。

筋、膠、混粘結界面上的裂紋尖端及周圍區域視為一個內聚力區，一般采用雙線性內聚力模型對粘結界面的黏結力進行分析和計算。圖4為雙線性張力-位移關系，其表示關系為：裂紋尖端內聚力區域內應力在外荷載的作用下，最初隨著位移的增加呈線性增長，張力達到最大值后，該處損傷開始萌生并擴展；此后隨著位移的增加張力值下降，該處承受荷載能力減小，裂紋進一步擴展；當應力減小至零，裂紋完全擴展，界面在該處開裂失效。

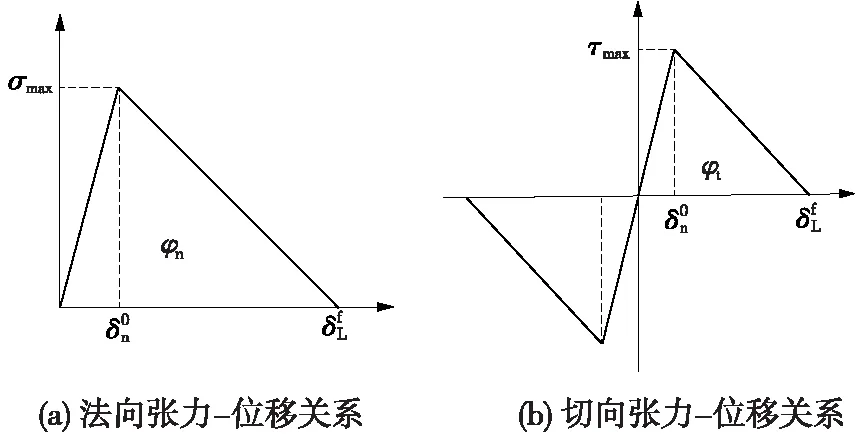
圖4 雙線性張力-位移關系

典型的雙線性內聚力模型的張力位移關系控制方程為

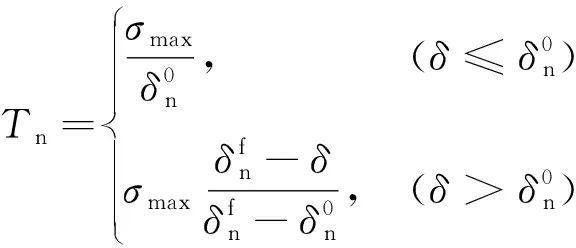
(4)

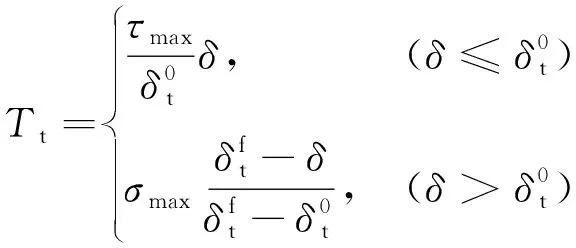
(5)

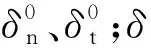
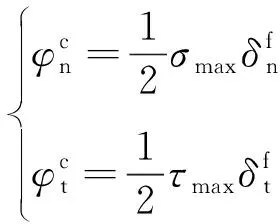
(6)

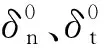
2.3 有限元模型的建立

考慮植筋錨固對基材混凝土的影響范圍，取植筋錨固連接及其周圍半徑150 mm的圓柱體基材混凝土作為研究對象。考慮到模型的對稱性，建立1/4模型。基材混凝土和植筋膠均采用Solid65三維混凝土實體單元；鋼筋采用Solid45三維實體結構單元。考慮到植筋膠層很薄也是關鍵結合處，將植筋膠的網格加密10倍。膠筋、膠混界面采用內聚力界面模型進行設置。利用Cohesive Zone(內聚力)理論對軌道板與植筋膠、砂漿層與植筋膠、底座板與植筋膠以及錨栓與植筋膠4個接觸界面設置垂向抗拉強度、切向抗拉強度、切向的斷裂能。圖5所示為CRTSⅡ型板式無砟軌道軌道板與底座板的錨固連接的有限元模型。

圖5 植筋錨固連接的有限元模型

3 植筋錨固連接的力學性能研究

以CRTSⅡ型板式無砟軌道軌道板與底座板的錨固連接為例研究植筋錨固的力學性能。植筋采用HRB500鋼筋，直徑28 mm，長度360 mm，錨固深度360 mm，錨孔直徑35 mm。植筋膠采用FISV360S植筋膠。主要參數見表1和表2。為了消除CA砂漿層與軌道板之間黏結力的影響，假定二者完全脫粘。

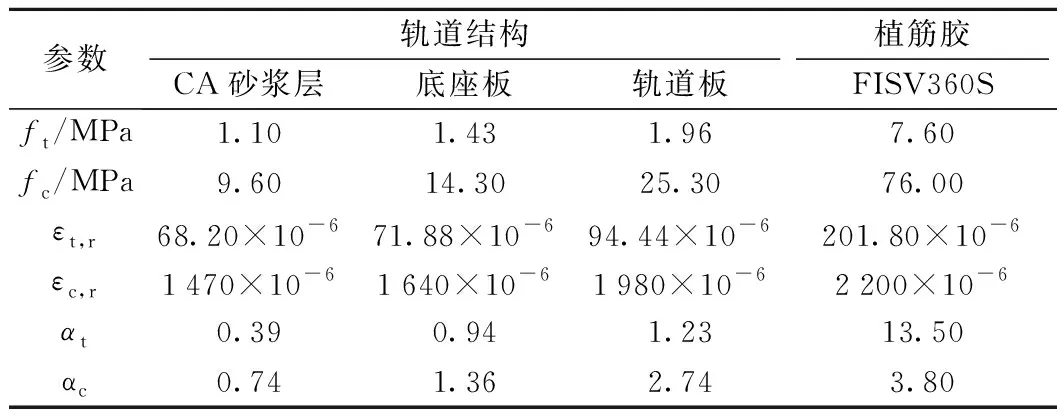
表1 植筋結構各部分主要參數取值

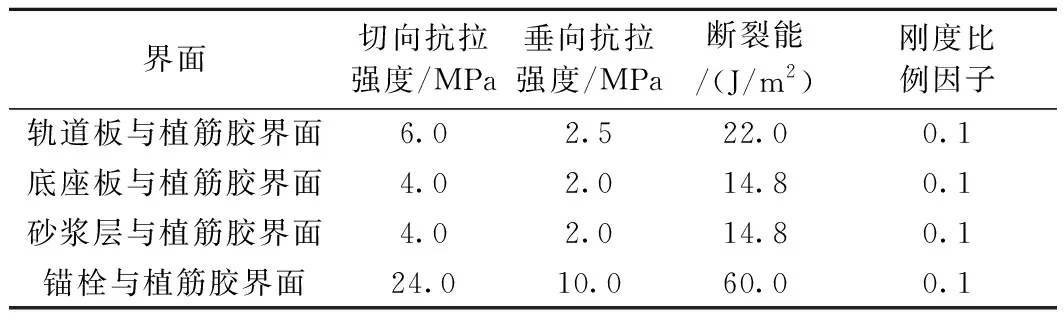
表2 界面模型(CZM)主要參數取值

3.1 抗拔力學性能

給軌道板按0.05 mm/步分步施加豎向向上的位移荷載，直至錨固連接破壞。提取豎向荷載、相對滑移值，可得植筋錨固連接的豎向荷載-滑移關系曲線(F-D曲線)，如圖6所示。結合加載過程中結構受力、變形動態云圖進行分析，得到如下結論。

(1)滑移量在0～0.35 mm時，F、D呈現線性關系，F-D曲線為過原點直線。此階段稱為彈性階段。在此階段，膠-混界面的變形處于彈性變形的范圍，界面不會出現損傷。

(2)滑移量在0.35～1.05 mm時，F-D曲線為一條拋物線，此階段為滑移階段：隨著植筋錨固連接所施加荷載的增大，底座板或CA砂漿層中膠-混界面出現的剪應力超過膠-混界面所能承受的最大剪應力，膠-混界面的加載區域開始產生裂縫，該區域界面剪應力開始降低，植筋錨固連接從彈性階段進入到塑性滑移階段。隨著荷載的進一步增大，塑性滑移區將不斷延伸，彈性變形區向自由端移動。當加載到某一臨界值時，植筋錨固連接某一截面剪應力降為0，該材料點破壞。隨著荷載的繼續增加，后面的界面粘結區域將成為新的初始承載點，膠-混界面剪應力由CA砂漿層與底座板界面位置處向錨固深度為360 mm方向平移。

(3)軌道板頂端滑移在1.05～1.35 mm，可視為一條斜線，該階段膠-混界面完全脫粘，此階段為破壞階段：在荷載超過限值后，膠-混界面剪應力由軌道板與CA砂漿層界面位置處向錨固深度為360 mm方向的平移也會達到極限狀態，剝離區域越來越長，彈性區域越來越短直至消失，只剩下剝離區段和塑性區段，在有效粘結長度末端截面，塑性區域也隨荷載的增加演變成剝離區段。至此，底座板與植筋膠界面完全破壞，錨栓與底座板、CA砂漿層完全脫粘，整個植筋錨固連接基本失效，繼續加載會由植筋膠與底座板、CA砂漿的摩擦力提供抗拔力，最終錨栓拔出。

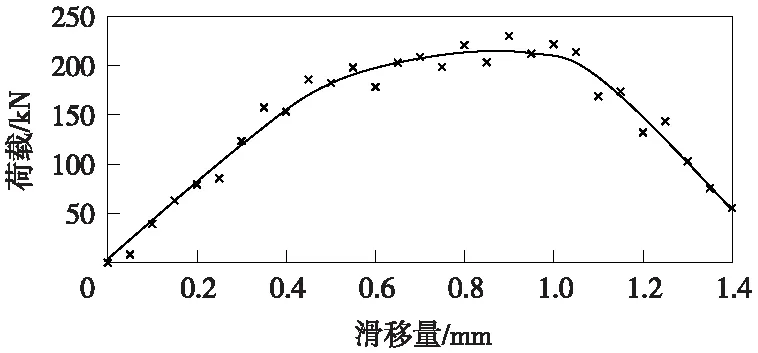
圖6 植筋錨固連接豎向荷載-滑移曲線

3.2 抗剪力學性能

給軌道板按0.1 mm/步分步施加水平位移荷載，直至錨固連接剪切破壞。提取橫向荷載、軌道結構間的摩擦力和相對滑移值，可得植筋錨固連接的水平荷載-滑移關系曲線(F-D曲線)，如圖7所示。

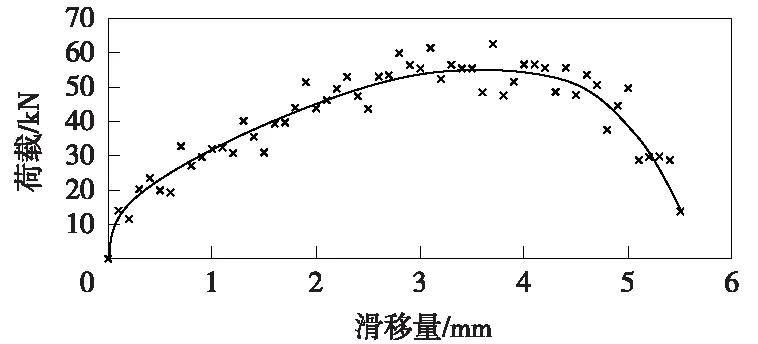
圖7 植筋錨固連接橫向荷載-滑移曲線

結合加載過程中結構受力、變形動態云圖進行分析，得到如下結論。

(1)滑移量在0～0.2 mm時，F、D呈線性關系，F-D曲線為過原點的直線，此為彈性階段。這一階段，植筋錨固連接的變形處于彈性變形范圍，錨栓不會因過大變形而產生損傷，卸載后界面能回到初始狀態。

(2)滑移量0.2～0.6 mm，曲線近似為拋物線，此階段稱為滑移階段。這一階段，荷載超過一定值后，膠-混界面出現裂縫，錨固連接的承載力逐步降低，局部范圍產生脫黏現象。

(3)滑移量在0.6～5.5 mm為破壞階段。滑移量在0.6～3.1 mm時可認為是一條直線，斜率小于初始階段。隨著橫向荷載增大，膠-混界面不會進一步脫黏，橫向荷載完全由錨栓和軌道層間摩擦力承擔，在軌道板與CA砂漿層界面處，錨栓發生彎曲；在滑移量達到3.1 mm后，繼續加載，錨栓將會發生屈服，植筋錨固連接的抗剪承載力不再增加。如果軌道板的位移超過一定限值，錨栓將被剪斷。

4 植筋錨固連接力學模型在軌道板上拱整治方案優化中的應用

軌道板在夏季高溫期間的上拱是我國南方地區CRTSⅡ型板式無砟軌道最突出的病害之一。一般采用軌道板與底座板間植筋錨固進行整治。某高速鐵路某段夏季最高溫時(軌道板溫升52 ℃)最大上拱達17.4 mm，最大縱向位移0.7 mm。圖8為仿真計算的軌道板位移云圖，與現場實測值基本吻合。

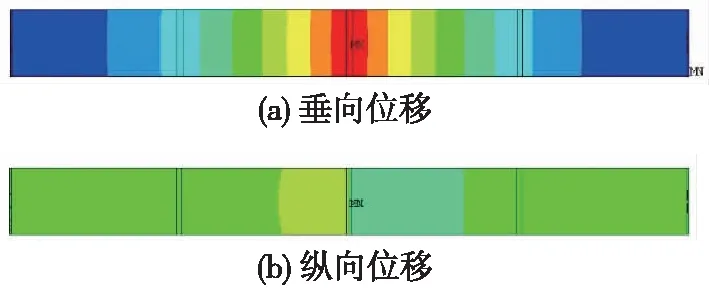
圖8 軌道板位移云圖(無植筋)

為整治軌道板上拱病害，初步擬定植筋錨固方案(圖9)。采用前述植筋錨固連接的力學模型進行仿真計算。圖10為軌道板位移云圖，軌道板最大豎向位移1.1 mm，減小93%，最大縱向位移為0.4 mm，降低26%。可見，植筋后軌道結構的位移得到有效控制。同時，可以方便地提取植筋錨固連接的受力，如圖11所示。對比各錨栓的受力，最大與最小抗拔力相差62%，最大與最小抗剪力相差64%。可見，各植筋連接的受力差異較大。

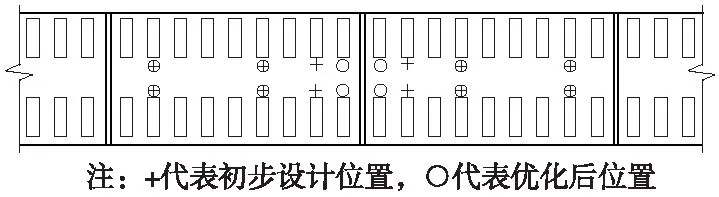
圖9 植筋錨固方案

圖10 軌道板位移云圖(初擬植筋方案)

植筋布置優化方案后(圖9)，從軌道板位移云圖(圖12)及植筋錨固連接受力(圖11)可見：軌道板垂向最大位移1.71 mm，最大縱向位移為0.44 mm，軌道板的位移控制較好；各植筋連接的受力差值減小，最大與最小抗拔力相差47.56%，最大與最小抗剪力相差43.58%，各植筋的性能均勻發揮。

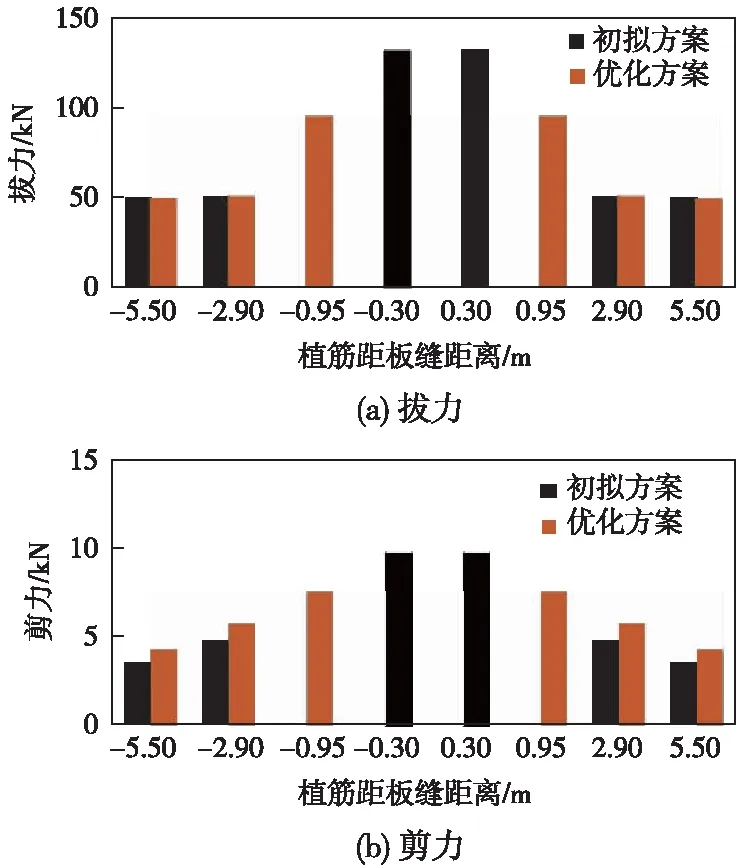
圖11 植筋受力示意

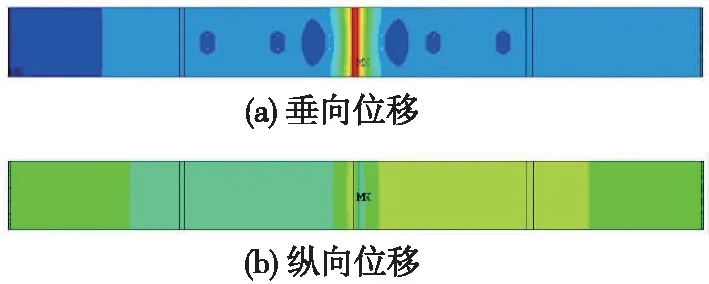
圖12 軌道板位移云圖(優化植筋方案)

5 結論

(1)將無砟軌道層間植筋錨固連接的抗拔和抗剪力學性能等效為彈簧，其縱向、橫向抗剪能力和豎向抗拔能力，分別等效為3個非線性軸向彈簧。這種方法可以簡化無砟軌道整體建模，提高計算效率。

(2)通過建立細觀尺度的植筋錨固連接精細化模型，對植筋連接的力學性能進行研究，獲取植筋錨固連接的荷載-滑移曲線，作為等效彈簧的荷載-位移特性曲線(F-D曲線)，避免了試驗時間和資金成本。

(3)CRTSⅡ型板式無砟軌道軌道板與底座板的錨固連接豎向荷載-滑移曲線以0.35，1.05 mm為節點分為3個階段，分別為彈性階段、滑移階段和破壞階段，植筋錨固連接發揮其抗拔作用效果主要在滑移階段。橫向荷載-滑移曲線以0.2，0.6 mm為節點分為3個階段，分別為彈性階段、滑移階段和破壞階段，植筋錨固連接發揮其抗剪作用效果主要在破壞階段的前期。

(4)通過軌道板上拱整治方案優化，建立的植筋錨固連接力學模型使無砟軌道層間植筋錨固連接的建模和計算效率提高，節約了試驗費用，具有較好的實用性。