新型干樹半潛式海洋平臺垂蕩運動性能研究

郭嘉寧，呂海寧，謝文會

(1. 上海交通大學 海洋工程國家重點實驗室，上海 200240; 2. 上海交通大學 三亞崖州灣深海科技研究院，海南 三亞 572024; 3. 上海交通大學 海洋裝備研究院，上海 200240; 4. 中海油研究總院有限責任公司，北京 100028)

用于深水油氣開發(fā)的生產井口系統(tǒng)有濕式采油樹和干式采油樹兩種，與濕式采油樹相比，干式采油樹既可用于鉆井也可用于完井生產，且易于管理、方便維修，還省去了將海底采油樹回接到平臺上部的硬件費用。目前，深水中采用干式采油樹并廣為使用的浮式平臺主要有張力腿平臺(tension leg platform，簡稱TLP)和Spar平臺。但當水深超過1 500 m時，TLP和Spar平臺不再適用干式井口[1]。因此對于深水海況，可將干式采油樹運用于深水半潛平臺，該種系統(tǒng)不僅具有干式井口的優(yōu)點，而且可消除TLP和Spar平臺的劣勢。同時，深水干樹半潛平臺擁有普通半潛平臺不受水深限制、造價低及安裝方便等特點。

針對干樹半潛平臺的概念，專家學者進行了研究設計。八角形概念浮式鉆井平臺[2]是世界上第一個干樹采油平臺，該平臺能夠應用于多種海洋環(huán)境，并且在建造、安裝、集成及選擇頂部張緊式立管(top tensioned riser，簡稱TTR)或鋼懸鏈線立管(steel catenary riser，簡稱SCR)方面具有很大的靈活性。Lu等[3]提出了雙立柱半潛平臺的設計概念，包括四個內立柱、四個主浮筒、四個外立柱和用來連接內外立柱的四個連接浮筒。Mansour等[4]提出一種新柱構型半潛平臺(damper chamber column semi)，該平臺有一個環(huán)形浮筒和四個立柱，此設計把每個立柱分為十個可提供浸水的內部阻尼室。紀亨騰等[5]提出了一種新型立柱類型，該設計區(qū)別于常規(guī)半潛平臺立柱的等截面形式，而是在不同吃水處采用不同的截面形式，立柱的底部截面積最大，向上逐漸變小。

由于干樹半潛平臺主要采用TTR，目前TTR的總沖程應限制在10 m以內[6]，立管沖程的主要影響因素是垂蕩運動，因此干樹平臺對垂蕩運動性能要求較高，其能否采用干式井口的主要標準就是垂蕩幅值是否足夠小[7]，在半潛平臺下部添加垂蕩板是抑制其運動的方法之一[8]。Peng等[9]提出了在傳統(tǒng)半潛平臺的基礎上，通過桿件將自由懸掛式固體壓載艙(solid ballast tank，簡稱SBT)和上部主體連接起來，結果顯示，這種設計能夠有效減小垂蕩響應，并確保了連接SBT和上部主體的桿件即使在極端海況下也處于張力狀態(tài)。Jiang等[10]提出了具有雙層浮筒的半潛平臺，兩層浮筒通過桿件剛性連接，探究了浮筒深度同垂蕩響應和連接處載荷的關系，說明了雙浮筒在改善平臺垂蕩性能中的作用。柳淑學等[11]研究了實心垂蕩板和開孔垂蕩板對Spar平臺水動力特性的影響，結果表明垂蕩板結構能有效提高Spar平臺的附加質量系數(shù)和黏性阻尼系數(shù)。

總體而言，目前對具有深吃水和大面積下浮箱兩個特點的干樹半潛平臺的研究較少。基于此，通過數(shù)值計算和模型試驗對新型干樹半潛式生產平臺[12]進行研究。平臺的垂蕩板具有較大的面積和質量，內部裝有壓載水，因此這里稱之為下浮箱(見圖1)。一方面下浮箱可以抑制垂蕩運動，另一方面需要足夠大質量的下浮箱以保證連接桿件能夠始終處于張力狀態(tài)，同時，可通過調節(jié)其中的壓載水重量以實現(xiàn)下浮箱的自安裝和在役狀態(tài)連接桿件的更換。該平臺的特點是通過類似張力腿的連接桿連接上部主體與下浮箱，使二者組成相互作用的耦合系統(tǒng)，連接點處采用可旋轉接頭，連接桿件可繞連接點轉動，釋放由下浮箱慣性力引起的巨大彎矩。下文研究了新型平臺的運動響應，并進一步對不同下浮箱放置深度進行了探索，以期為新型干樹半潛平臺的優(yōu)化和使用提供參考。

圖1 平臺主體結構型式Fig. 1 Main structure type of the platform

1 干樹半潛平臺數(shù)值計算理論

1.1 三維勢流理論

采用三維勢流理論來計算大尺度結構物濕表面上的波浪載荷，假定流體為理想流體，即均勻、不可壓縮、無黏、無旋。速度勢滿足拉普拉斯方程、海底邊界條件、自由面邊界條件、物體濕表面運動邊界條件及輻射條件[13]。根據(jù)拉普拉斯方程和邊界條件唯一確定速度勢，之后由伯努利方程計算出結構物濕表面上的壓強，進而求出結構物所受到的波浪載荷[14]。

流場中的總速度勢：

Φ(x,y,z)=Re[(ΦI(x,y,z)+ΦD(x,y,z)+ΦR(x,y,z))e-iωt]

(1)

式中：ΦI(x,y,z)為入射勢，ΦD(x,y,z)為繞射勢，ΦR(x,y,z)為輻射勢，e-iωt為時間因子。

下面為進行計算必須滿足的邊界條件：

1) 自由面條件

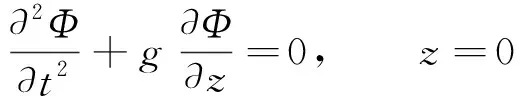
(2)

2) 物面條件

(3)

3) 水底條件

假設海底為水平面，則底面邊界條件：

(4)

4) 輻射條件

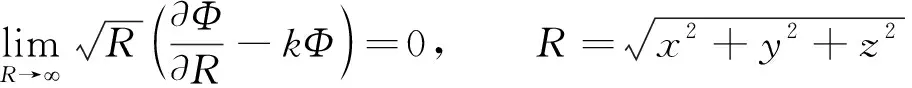
(5)

式中：g為重力加速度，n為物體濕表面外法向量，un為物體沿n方向的運動速度，h為水深，k為波數(shù)。

1.2 頻域運動控制方程

干樹半潛平臺在整體坐標系統(tǒng)中考慮所受到的激勵力、阻尼和附加質量的頻域運動控制方程：

[-ω2(M+A(ω))+iω(B(ω)p+Bv)+Cij]X(ω,β)=F(ω,β)

(6)

式中：M為質量和慣量矩陣，A(ω)為附加質量矩陣，B(ω)p為勢流阻尼矩陣，Bv為線性化后的黏性阻尼矩陣，Cij為靜水回復力系數(shù)矩陣，F(xiàn)(ω,β)為外部激勵力矩陣。

1.3 時域運動控制方程

對海洋結構物進行時域計算時，需要綜合考慮風載荷、浪載荷、流載荷及系泊力的聯(lián)合作用。與頻域計算相比，時域計算更為精確。干樹半潛平臺的時域運動方程[15]：

(7)

式中：mij為平臺的質量矩陣，uij為附加質量矩陣，Lij(t-τ)為平臺系統(tǒng)的延遲函數(shù)，Cij為靜水回復力系數(shù)矩陣，F(xiàn)ωa(1)(t)為一階波浪載荷，F(xiàn)ωa(2)(t)為二階波浪載荷，F(xiàn)ωi(t)為風載荷，F(xiàn)cu(t)為流載荷，F(xiàn)mo(t)為系泊系統(tǒng)對平臺的作用力。其中，F(xiàn)ωa(2)(t)僅考慮二階差頻波浪力(忽略二階和頻波浪力)，在二階平均波浪力的基礎上采用Newman近似方法[16]計算得到。

2 研究對象

2.1 坐標定義

水池模型試驗中，采用大地坐標系(全局坐標系)O-XYZ，以及平臺主體局部坐標系o1-x1y1z1，下浮箱局部坐標系o2-x2y2z2共三個坐標系，定義如圖2所示。

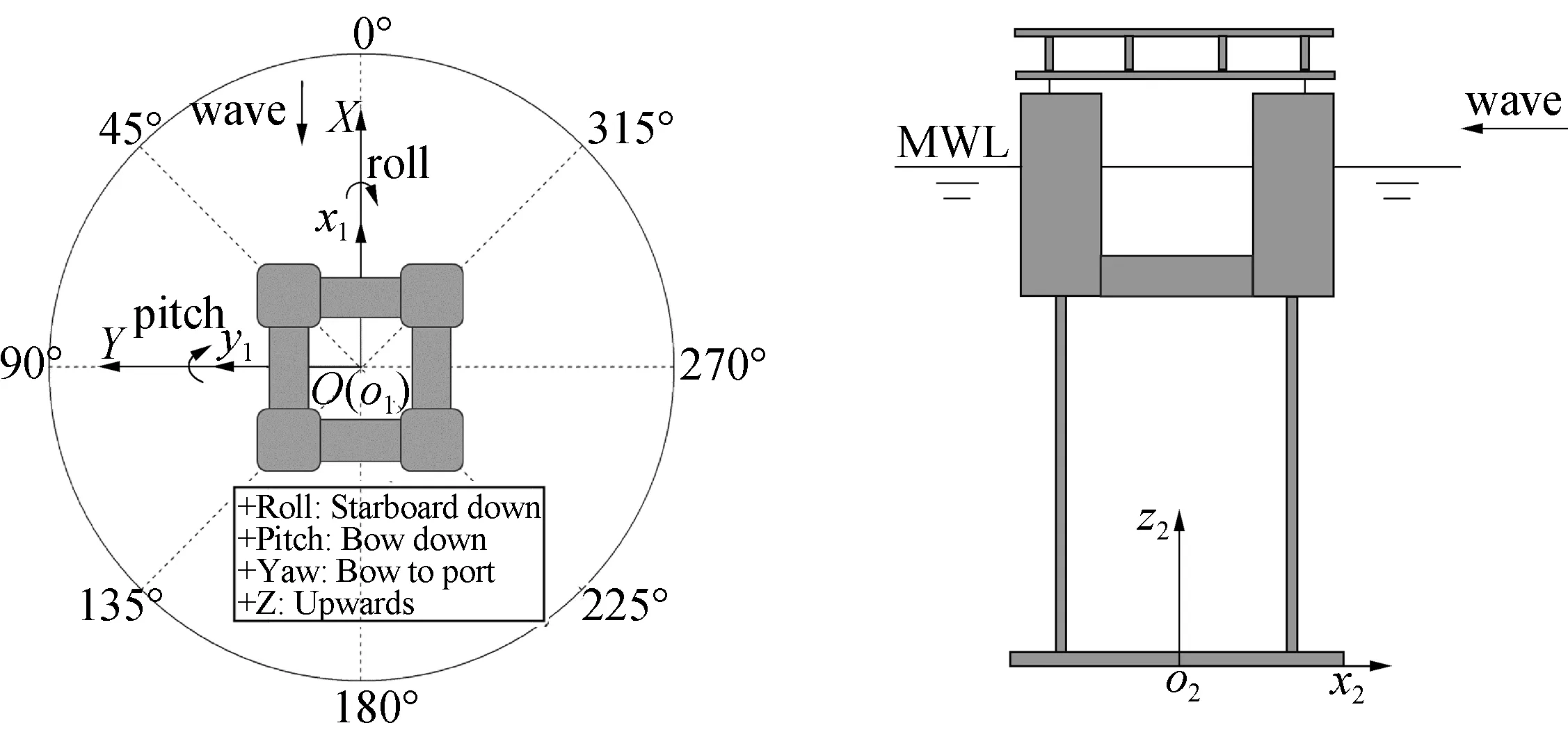
圖2 平臺形狀及坐標系定義Fig. 2 Shape and coordinate system definition of the platform

2.2 模型參數(shù)

平臺模型包括上部主體、下浮箱、連接桿件和立管系統(tǒng)。其主要參數(shù)分別如表1和表2所示。

表1 上部主體主要參數(shù)

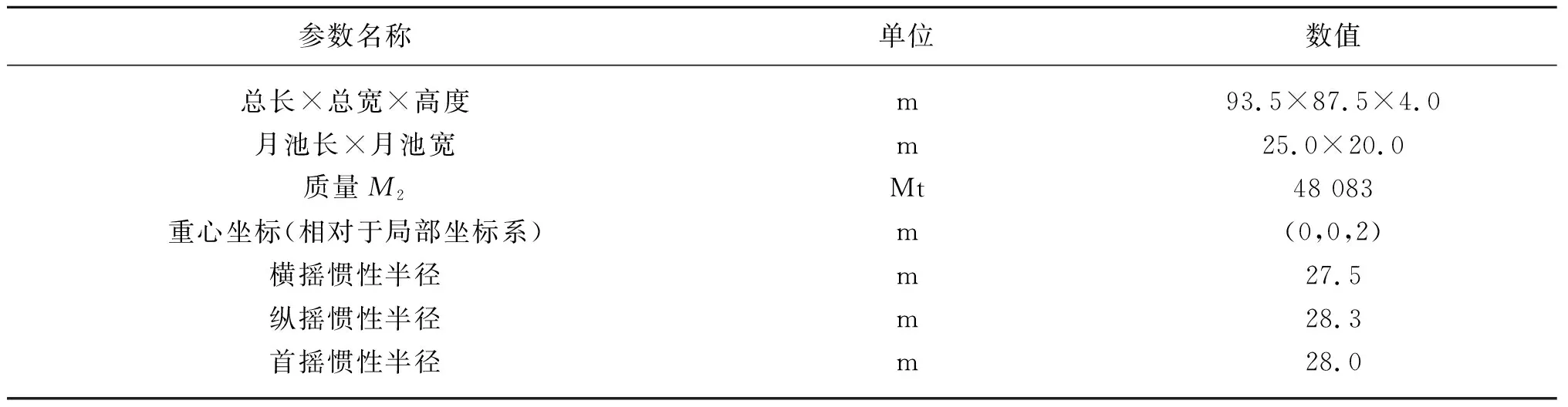
表2 下浮箱主要參數(shù)

其中，連接桿件共有8根，長度均為100 m；TTR立管共有12根；系泊纜共有4組，每組4根，每條均采用“鏈—纜—鏈”形式，相鄰組系泊纜之間的夾角為90°，同組相鄰系泊纜之間的夾角為5°。連接桿件、TTR立管和系泊系統(tǒng)的相對位置如圖3所示。

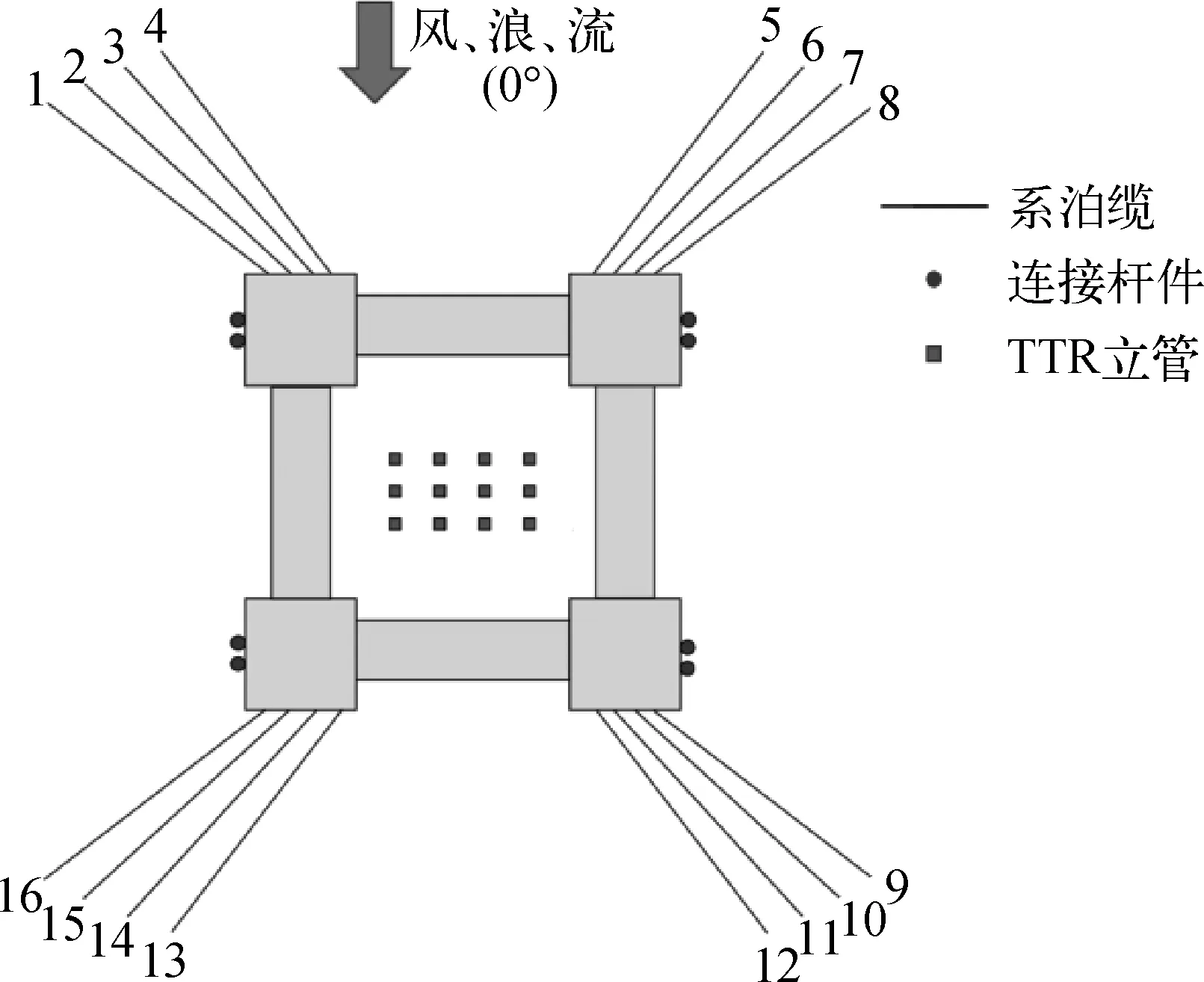
圖3 連接桿件、TTR立管及系泊系統(tǒng)布置Fig. 3 Connecting rods, TTR risers and mooring system

2.3 數(shù)值模擬

基于勢流理論，采用HydroD軟件計算頻域水動力參數(shù)，包括運動響應及波浪力傳遞函數(shù)等；使用Orcaflex軟件在時域內對整個系統(tǒng)進行模擬，包括平臺主體、連接桿件、立管系統(tǒng)及系泊定位系統(tǒng)，充分考慮各成分間的非線性耦合效應。在進行網格劃分時，將面元網格大小設置為2 m×2 m。考慮平臺結構的對稱性，在頻域計算時選定波浪入射角為0°至90°，步長為15°，共7種波浪入射角度；同時選定入射波浪周期為3 s至40 s。將頻域計算得到的輸出文件導入Orcaflex進行時域分析，模擬時間為10 800 s，時間步長為0.2 s，過渡時間為200 s，頻域及時域數(shù)值模型如圖4所示。

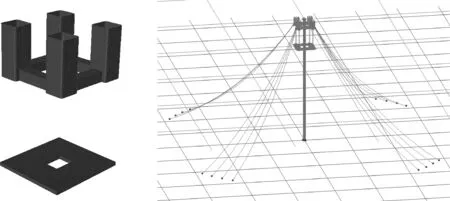
圖4 頻域及時域數(shù)值計算模型Fig. 4 Numerical model in frequency-domain and time-domain

在考慮下浮箱的阻尼系數(shù)和質量力系數(shù)時，由于該下浮箱與普通垂蕩板不同，具有較大的面積和質量，因此采用CFD方法來估算阻尼系數(shù)和質量力系數(shù)，最終選定下浮箱水平向阻尼系數(shù)為1.0，垂向阻尼系數(shù)為4.0，選定質量力系數(shù)為1.5。

時域計算工況如表3所示，工況1～6與模型試驗工況相同，共選取三個浪向角來探究其對平臺運動性能的影響。風浪流環(huán)境條件均為百年一遇，以探究平臺在極端海洋環(huán)境條件下的性能。工況7～15為探究平臺在不同環(huán)境條件下的垂蕩運動，即垂蕩響應與有效波高之間的關系。工況16～21為探究平臺在不同下浮箱放置深度下的垂蕩運動性能。

表3 時域計算工況

3 模型試驗

為驗證數(shù)值模擬方法的準確性，在海洋工程深水試驗池中進行了模型試驗(見圖5)，水池尺寸為50 m×40 m×10 m(長×寬×深)，模型縮尺比選定為1∶60。試驗選取三種典型海洋環(huán)境條件、兩種下浮箱放置深度，共六個工況，如表4所示，考察不同環(huán)境條件下干樹半潛平臺的運動響應。不規(guī)則波浪采用Jonswap波浪譜，風浪流方向一致。

圖5 模型試驗Fig. 5 Model test

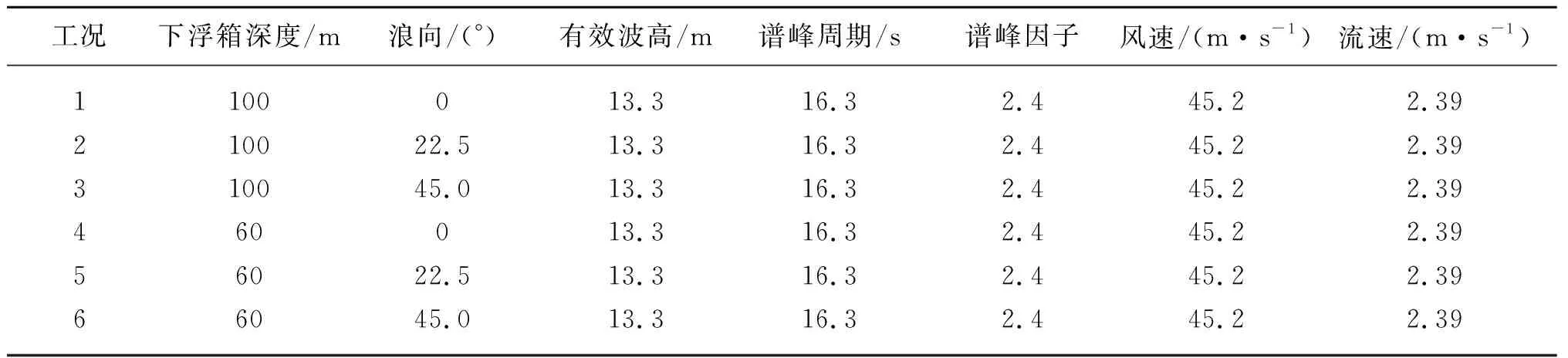
表4 水池試驗工況

4 結果與分析

4.1 下浮箱對平臺垂蕩性能的影響

圖6為通過頻域數(shù)值模擬得到的浪向角45°時平臺在有下浮箱(下浮箱放置深度為100 m)和無下浮箱時的幅值響應算子曲線。由數(shù)值結果可以看出，當沒有下浮箱時平臺的垂蕩運動固有周期在19.0 s左右，而常見波周期范圍在5～25 s，因此該平臺會有較大的垂蕩響應。有下浮箱時平臺的垂蕩運動固有周期在30.0 s 左右，避開了常見波周期范圍，有較小的垂蕩響應。根據(jù)試驗結果，平臺的縱蕩、橫蕩、垂蕩固有周期分別為138.2 s、137.6 s、29.2 s；橫搖、縱搖、首搖固有周期分別為34.1 s、33.2 s、88.8 s。

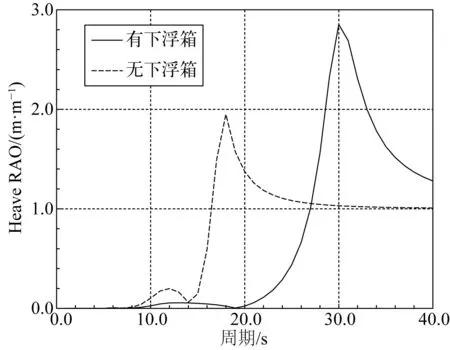
圖6 平臺幅值響應算子曲線Fig. 6 Amplitude response operator curves of the platform

下浮箱通過增大平臺的附加質量和運動阻尼來改變垂蕩固有周期，從而達到改善平臺垂蕩運動的目的。圖7和圖8比較了頻域模擬得到的有無下浮箱時平臺垂蕩附加質量和輻射阻尼系數(shù)的變化，可以看出，該下浮箱極大地提高了平臺的垂蕩附加質量。當周期在5.0～10.5 s時，平臺輻射阻尼系數(shù)基本不受下浮箱的影響；當周期在10.5～16.0 s時，下浮箱的存在增大了平臺的垂蕩輻射阻尼；但當周期大于16.0 s時，下浮箱的存在反而降低了平臺的垂蕩輻射阻尼。輻射阻尼系數(shù)與物體的形狀有很大關系，就該新型平臺而言，下浮箱的存在極大地影響了平臺的垂蕩附加質量，但對輻射阻尼系數(shù)的影響較小(圖7及圖16中A33是平臺的垂蕩附加質量)。

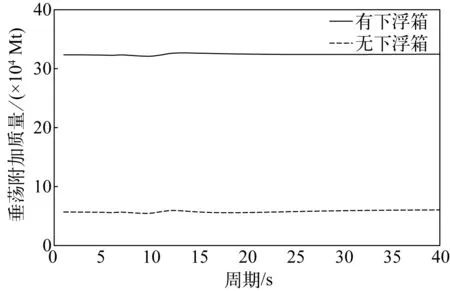
圖7 平臺垂蕩附加質量(A33)Fig. 7 Added mass of the platform in heave (A33)

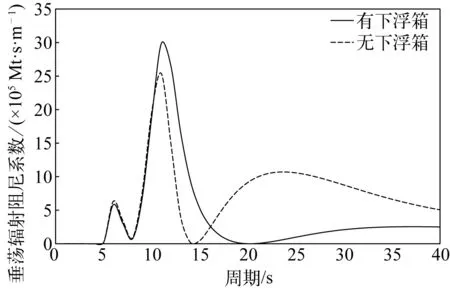
圖8 平臺輻射阻尼系數(shù)Fig. 8 Radiation damping coefficients of the platform

圖9和圖10為通過時域模擬得到的工況3海洋環(huán)境條件下平臺的垂蕩運動時歷曲線。當沒有下浮箱時平臺的垂蕩運動極值約為7.8 m，垂蕩響應范圍為14.2 m；當有下浮箱時平臺的垂蕩運動極值僅為1.8 m左右，垂蕩響應范圍為3.3 m。配置下浮箱之后，平臺的垂蕩運動極值和垂蕩響應范圍分別下降76.9%和76.7%，可見，下浮箱能夠極大地改善平臺的垂蕩運動性能。

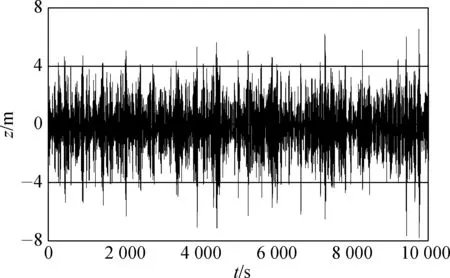
圖9 無下浮箱時垂蕩運動時歷曲線Fig. 9 Time history curve of heave without lower pontoon

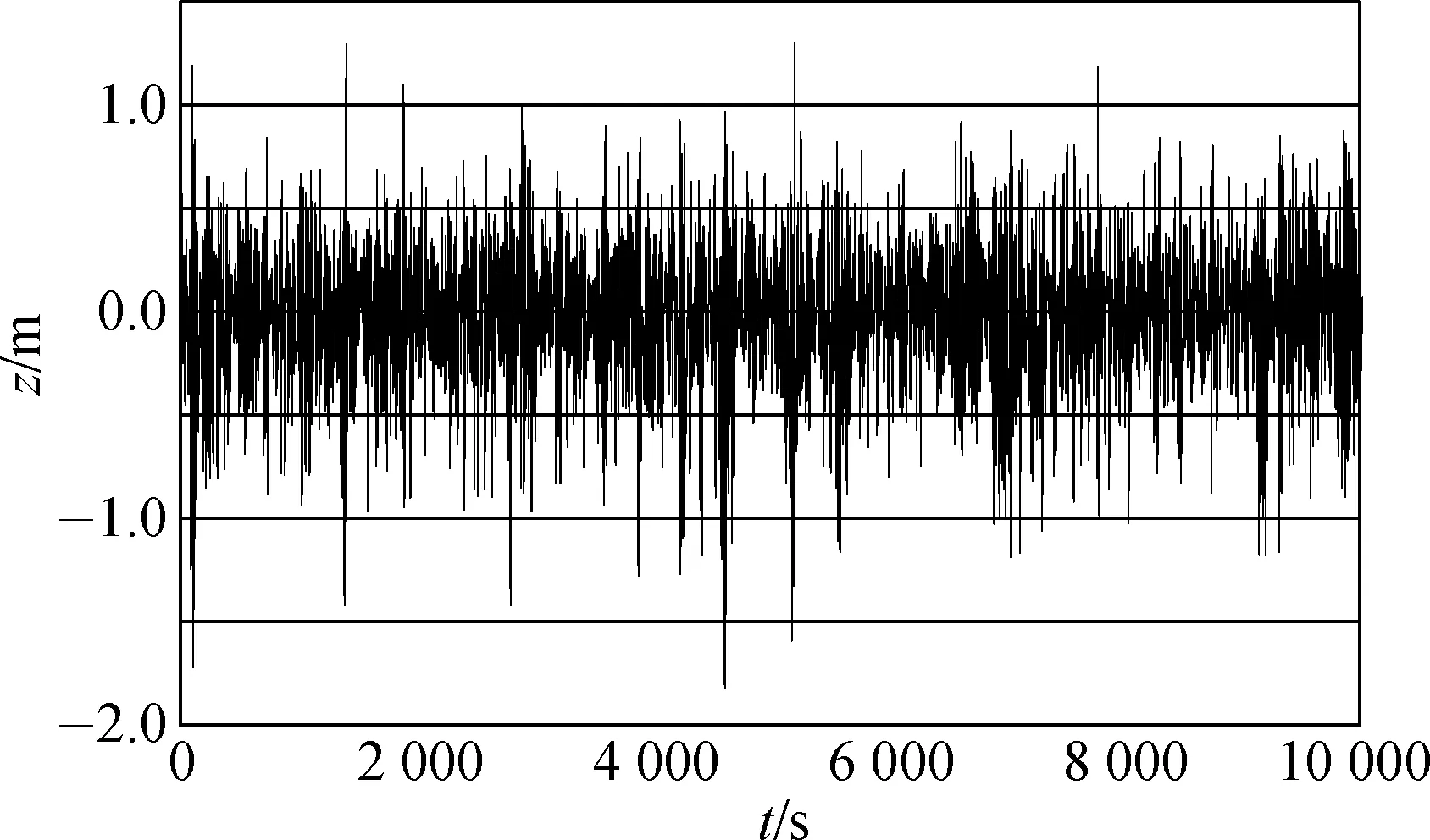
圖10 有下浮箱時垂蕩運動時歷曲線Fig. 10 Time history curve of heave with lower pontoon

4.2 不同海況下平臺垂蕩運動響應

對新型干樹半潛平臺開展時域計算，計算工況見表3，模擬時長為3 h。圖11為數(shù)值模擬和試驗下，平臺垂蕩響應時歷曲線與對應頻率譜結果對比。表5為相應的垂蕩運動響應統(tǒng)計值對比。

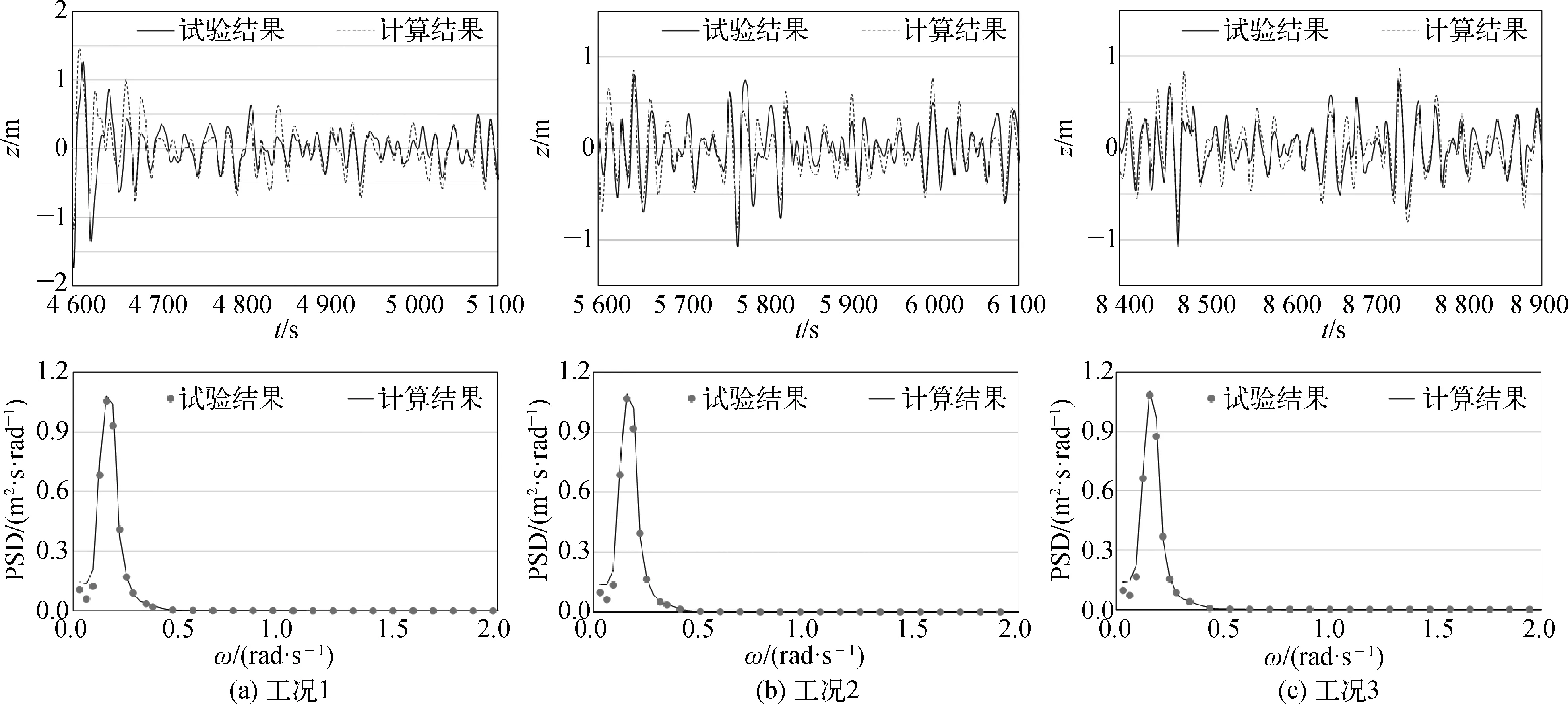
圖11 垂蕩運動響應時歷及頻率譜(放置深度100 m)Fig. 11 Time history and power spectrum density (PSD) curves of heave motion

表5 垂蕩運動響應統(tǒng)計值

圖11及表5表明數(shù)值計算結果同試驗所得結果基本一致，說明采用頻域和時域相結合的方法可靠，能夠正確反映平臺的運動響應特性。且由表4及表5可以看出，隨著浪向角的增大，垂蕩運動響應范圍有增大趨勢，這是因為當浪向角增大時，平臺的迎浪面積也隨之變大，導致平臺垂蕩運動顯現(xiàn)增大趨勢。

為進一步探究不同海況對平臺垂蕩運動響應的影響規(guī)律，對幾種工況(見表3中工況7～15)下平臺垂蕩運動響應展開了時域計算，結果如圖12所示。現(xiàn)有結果表明，平臺垂蕩運動響應幅值與有效波高之間基本呈線性關系，這是因為該平臺水動力分析過程中計算運動響應時采用的是線性勢流理論。

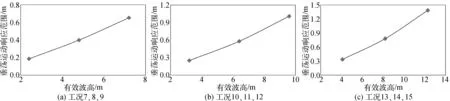
圖12 不同海況下平臺垂蕩運動幅值Fig. 12 Amplitudes of platform heave motion under different sea conditions

4.3 下浮箱放置深度對平臺垂蕩運動的影響

為探究下浮箱在上部主體之下深度變化對垂蕩響應的影響，選取了0～140 m(間隔為20 m)共8種不同的深度，分析平臺在工況16～21環(huán)境條件作用下的垂蕩響應。其中，深度為60 m和100 m時分別做了相應的模型試驗，基于試驗結果對其他下浮箱放置深度下平臺的垂蕩響應展開了時域數(shù)值計算。放置深度是下浮箱位于上部主體之下的深度，放置深度為100 m時的計算結果和試驗結果對比已于4.2節(jié)展示，圖13、表6展示了放置深度為60 m時模型試驗結果和數(shù)值結果的對比。

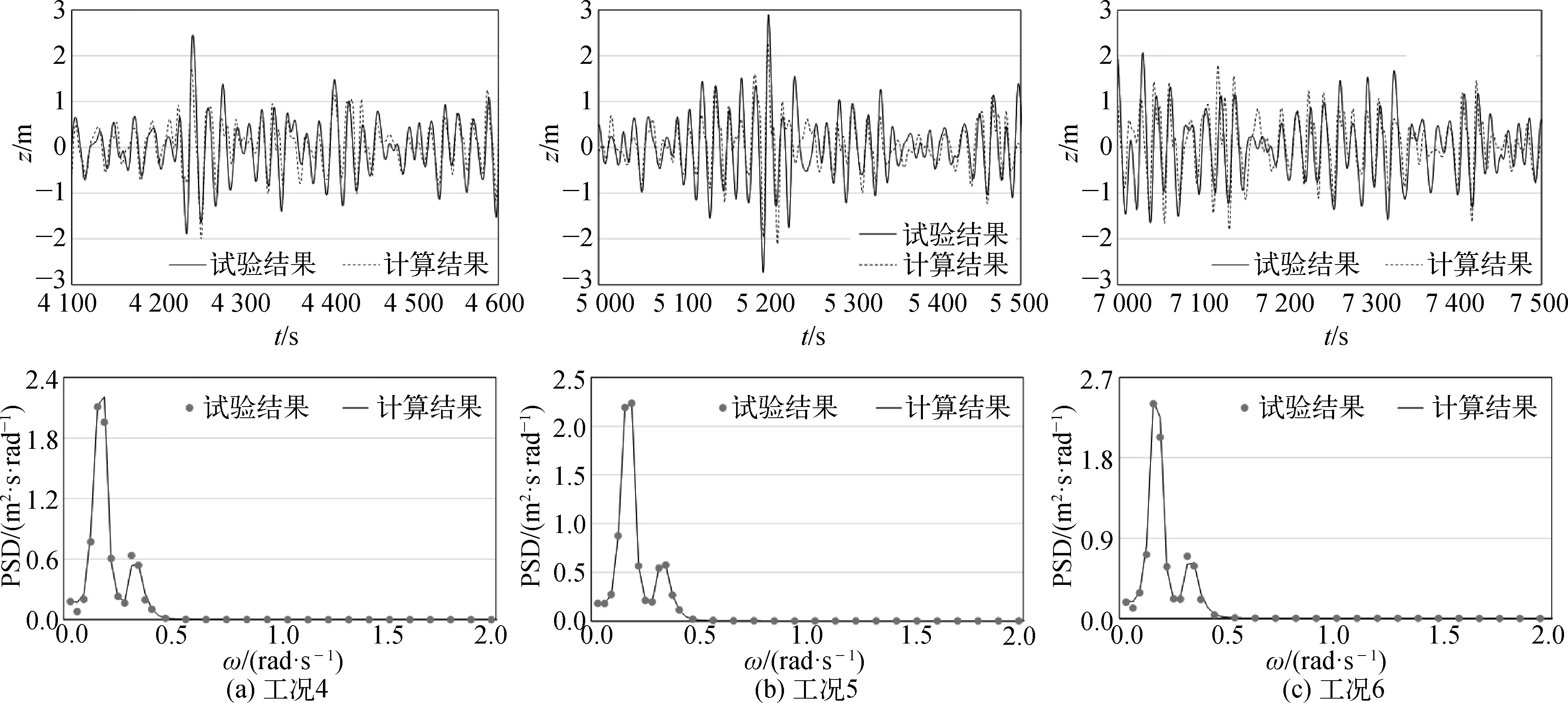
圖13 垂蕩運動響應時歷及頻率譜(放置深度60 m)Fig. 13 Time history and power spectrum density (PSD) curves of heave motion

計算結果表明，將下浮箱放置深度設置為20 m時，相比無下浮箱的情況，平臺的垂蕩響應得到一定改善。隨著放置深度的增大，平臺的垂蕩運動極值呈減小趨勢。在放置深度從20 m增大到80 m的過程中，垂蕩運動極值減小幅度大于放置深度從80 m增大到140 m的過程。當放置深度在100 m至140 m之間變化時，垂蕩運動極值變化不明顯(見圖14)。由水波理論可知，在這些工況下，當水深大于207 m時即可近似為無限水深問題。考慮上部主體吃水和下浮箱高度，當下浮箱放置深度大于167 m時，水面波動不再對其運動產生影響，因此會出現(xiàn)隨著放置深度增大，下浮箱對平臺運動性能影響減弱的現(xiàn)象。

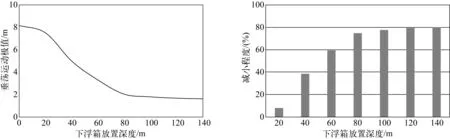
圖14 平臺垂蕩運動極值及相比無下浮箱減小程度(放置深度0 m時為無下浮箱)Fig. 14 Extreme values of heave motion and the degree of reduction compared with no lower pontoon (no lower pontoon when placed at a depth of 0 m)

該下浮箱的設置極大地增加了平臺的附加質量，從而延長垂蕩固有周期，達到有效抑制浮體垂蕩運動的目的。圖15得到了下浮箱不同放置深度下平臺的幅值響應算子曲線，圖16得到了平臺垂蕩附加質量隨放置深度的變化。由表7及圖15、圖16可以看出，隨著下浮箱放置深度的增大，平臺的垂蕩附加質量逐漸增大，同時，垂蕩運動固有周期也呈增大趨勢。其固有周期的變化規(guī)律與平臺垂蕩運動極值和響應范圍的變化趨勢基本吻合。

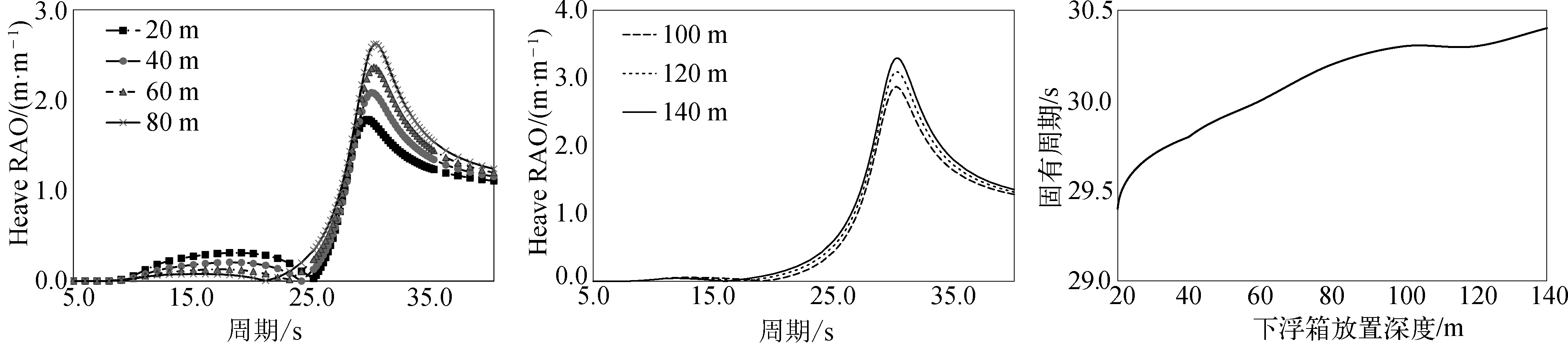
圖15 下浮箱不同放置深度下平臺垂蕩響應RAO及垂蕩固有周期Fig. 15 Heave RAO and natural period of heave at different placement depths of lower pontoon

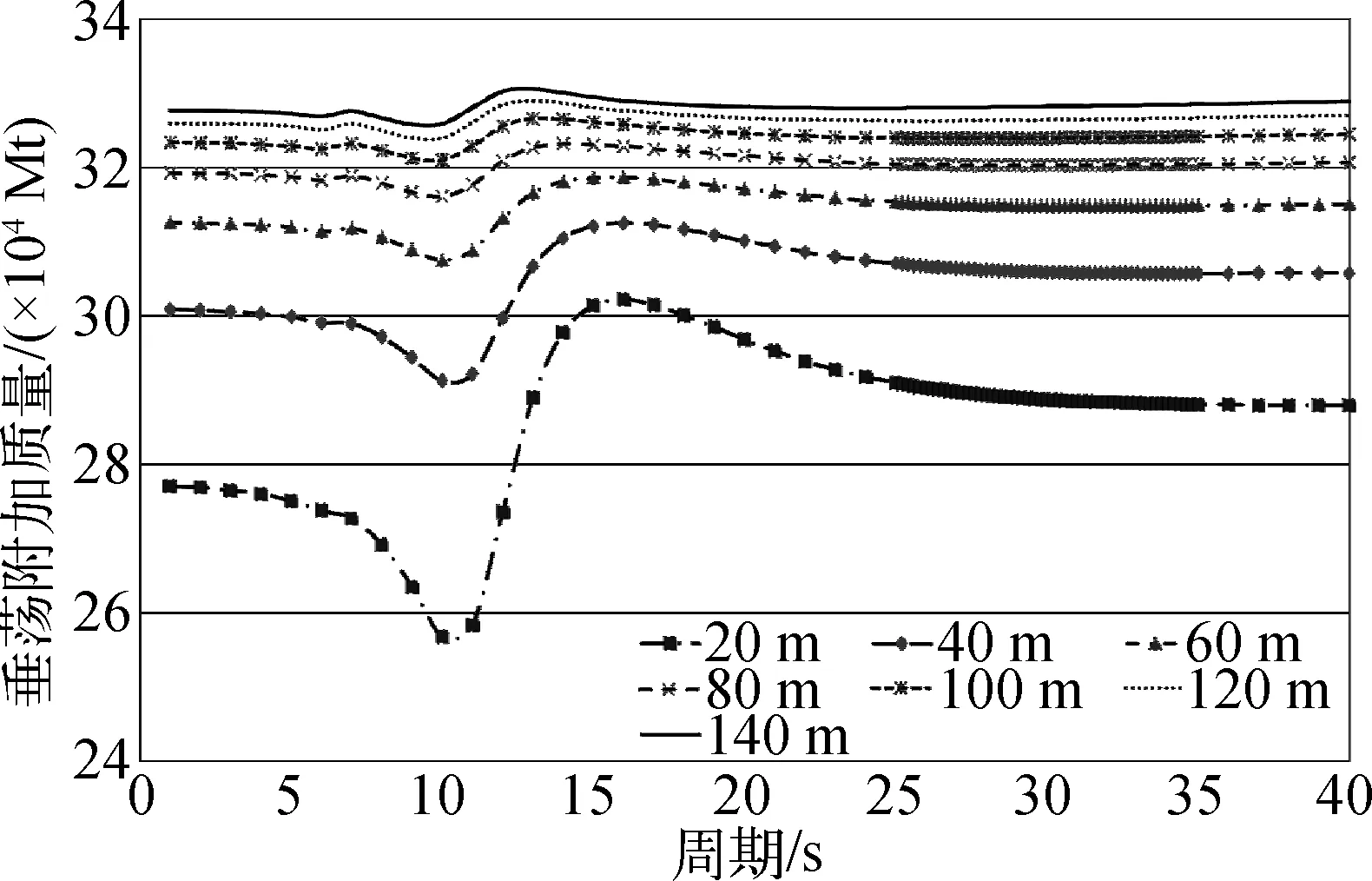
圖16 下浮箱不同放置深度下平臺垂蕩附加質量(A33)Fig. 16 Added mass of the platform in heave at different placement depths of lower pontoon (A33)

表7 下浮箱不同放置深度下平臺垂蕩響應統(tǒng)計值

雖然可通過增大下浮箱放置深度的方式來提升下浮箱的作用，但并不是放置深度越深越好，一是當放置深度大于100 m后，垂蕩固有周期增加不明顯，且幅值響應算子有增大趨勢，這對垂蕩抑制作用不利；二是隨著放置深度的增加，建造和安裝更加困難，同時對連接平臺上部主體和下浮箱的構件特性有更高要求。下浮箱放置深度為100 m時平臺的垂蕩運動固有周期已遠離了波浪主能量周期范圍，且此時平臺在極端海況作用下垂蕩運動極值不大于1.8 m，極大降低了TTR沖程，滿足干樹半潛平臺對垂蕩運動性能的要求。綜合考慮各方面因素，下浮箱的最佳放置深度為100 m。

5 結 語

采用模型試驗和數(shù)值模擬相結合的方法，對兼具深吃水和大面積下浮箱兩個特點的新型干樹半潛平臺的垂蕩運動性能展開了研究，探究了有無下浮箱及下浮箱放置深度對平臺垂蕩運動響應的影響。并在此基礎上，對不同海況下平臺的垂蕩運動進行了分析，得出以下結論：

1) 通過設置下浮箱，平臺的垂蕩固有周期增大了50%，垂蕩運動極值和響應范圍減小了70%以上，極大地改善了平臺的垂蕩運動性能；

2) 下浮箱的存在極大地增加了垂蕩附加質量，增大了平臺的垂蕩運動固有周期，從而達到改善平臺垂蕩運動性能的目的；

3) 通過對不同海況下平臺垂蕩運動響應進行探究，發(fā)現(xiàn)海況在小范圍內變化時，垂蕩運動幅值與波高之間基本呈線性關系；

4) 隨著下浮箱放置深度的增大，平臺的垂蕩運動極值逐漸減小，放置深度在20～100 m之間時，呈現(xiàn)線性減小趨勢，當放置深度超過100 m后，減小幅度不明顯；

5) 綜合考慮平臺運動性能和工程實際應用條件，下浮箱的最佳放置深度為100 m。