類正弦定理猜想的否定

甘志國

(北京豐臺二中 100071)

筆者在文[1]中提出了如下猜想：

類正弦定理猜想在△ABC中，若滿足下列條件之一，則A=B=C：

下面的定理3，4，5,6,7(其證明只用到了三角函數的恒等變形)分別否定了類正弦定理猜想的(1)(2)(3).

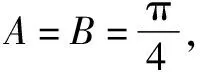
證明由題設及三角形內角和定理、正弦定理，可得

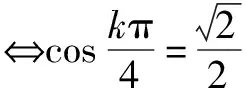
?k=8n±1(|n|∈N*).

證明由題設及三角形內角和定理，得

=0(k≠1.5n,n∈Z)

?k=12n±1(n∈Z)

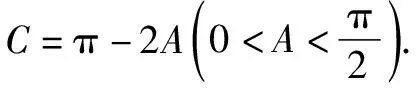
由正弦定理，可得

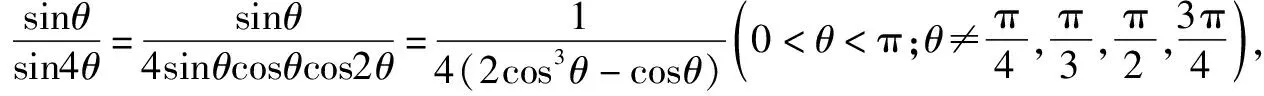
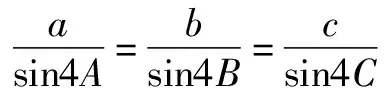
?2cos3A-cosA=2cos3C-cosC

?2cos3A-cosA=2cos3(π-2A)-cos(π-2A)

?2cos3A-cosA=-2(2cos2A-1)3+(2cos2A-1)

所以欲證結論成立.

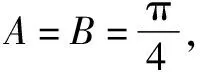
證明由題設及三角形內角和定理、正弦定理，可得

進而可得欲證結論成立.

證明由題設及三角形內角和定理、正弦定理，可得

進而可得欲證結論成立.

以上研究可能離高中數學教學有點遠，但下面的三道原創題是適合有興趣的高中師生練習的.

題1在△ABC中，角A,B,C的對邊分別是a,b,c.

(1)請選擇下面的一個條件，證明A=B=C.

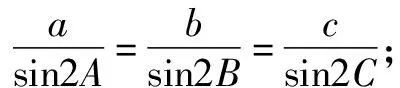
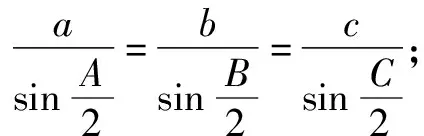
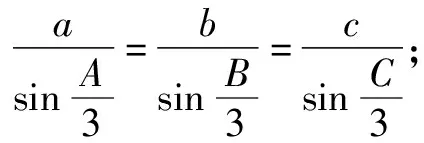
題2在△ABC中，角A,B,C的對邊分別是a,b,c.

(1)請選擇下面的一個條件，證明A=B=C.

題3在△ABC中，角A,B,C的對邊分別是a,b,c.

(1)請選擇下面的一個條件，證明A=B=C.

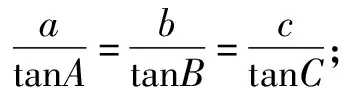
題1的參考答案(1)見文[1]中對開頭題目的解答及定理1[1]的證明.

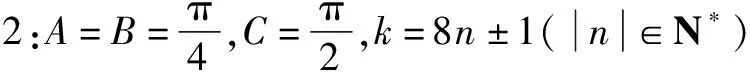
題2的參考答案(1)見文[1]中對開頭題目的解答.

題3的參考答案(1)見文[1]中對開頭題目的解答及定理2的證明.