數(shù)列與其他知識的交匯

徐 燕

(浙江省杭州市蕭山區(qū)第三高級中學 311200)

“從學科的整體高度和思維價值的高度考慮問題，在知識網(wǎng)絡交匯點處設計試題，使對數(shù)學基礎知識的考查達到必要的深度.”這是高考對數(shù)學知識點間的交匯的總體指導思想，有效交匯知識，創(chuàng)新應用，在高考中出現(xiàn)的頻率越來越多.以數(shù)列為背景，與集合、不等式、算法、解三角形、數(shù)學文化等知識與背景的交匯，更是數(shù)列問題中的重點與交匯所在，是高考中的熱點與亮點之一.

一、數(shù)列與集合的交匯

例1(江蘇省南通等七市2019屆高三第二次調研測試·14)已知集合A={x|x=2k-1，k∈N*}，B={x|x=8k-8，k∈N*}，從集合A中取出m個不同元素，其和記為S；從集合B中取出n個不同元素，其和記為T.若S+T≤967，則m+2n的最大值為____.

分析根據(jù)題目條件，要使得代數(shù)式m+2n取得最大值，一定是集合A中最小的m個不同元素與集合B中最小的n個不同元素的和，進而結合數(shù)列求和建立相應的不等式，配方處理，再利用基本不等式的轉化，求解二次不等式，得到關系式的最值問題.要注意參數(shù)m，n必須是正整數(shù)的取值限制，對相應的最大值要加以合理調整.

解析根據(jù)題目條件，要使得m+2n取得最大值，一定是集合A中最小的m個不同元素與集合B中最小的n個不同元素的和，即(2×1-1)+(2×2-1)+(2×3-1)+…+(2m-1)+(8×1-8)+(8×2-8)+(8×3-8)+…+(8n-8)≤967，整理有m2+4n2-4n≤967，配方可得m2+(2n-1)2≤968.

點評巧妙以集合為問題背景，通過數(shù)列與集合等不同知識點、不同數(shù)學思想方法的有機融合與交匯，提升數(shù)學知識點的深度與廣度，更有效考查數(shù)學能力與創(chuàng)新應用，因而備受命題者的青睞.

二、數(shù)列與不等式的交匯

A.d<0 B.d>0 C.a1d<0 D.a1d>0

分析利用條件中的遞增數(shù)列的性質建立對應的不等式，結合指數(shù)不等式的轉化與應用，結合通項公式加以變形與轉化，利用等價變形得到相應的不等關系式.

解析由于{ea1an}是遞增數(shù)列，可得ea1an0，故選D.

點評利用數(shù)列的基本性質(包括單調性、周期性等)來巧妙設置，特別結合單調性這一基本性質，可以進一步融合與交匯不等式問題.此類問題在解決數(shù)列問題中經(jīng)常會加以涉及與應用.

三、數(shù)列與算法的交匯

例3閱讀如圖1所示的算法流程圖，執(zhí)行程序后輸出的S的值是____.

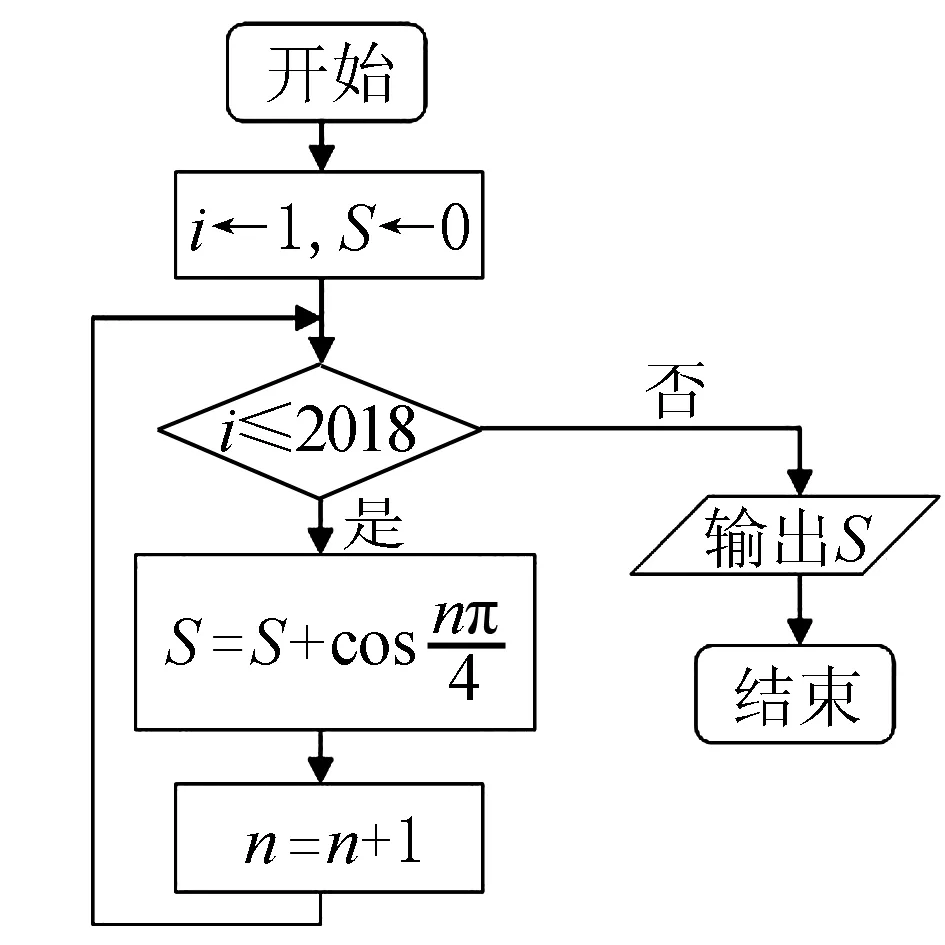
圖1

分析識別算法流程圖，確定程序的基本功能是數(shù)列求和，確定起止參數(shù)，建立數(shù)列求和的關系式，結合三角函數(shù)規(guī)律與性質加以合理運算.

在2018云南企業(yè)100強、制造業(yè)企業(yè)50強榜單中，云南祥豐實業(yè)集團有限公司位列云南企業(yè)100強第34位，位列云南制造業(yè)50強第14位。

點評以算法背景與循環(huán)結構的設置來建立數(shù)列的求和關系，巧妙融入三角函數(shù)的圖象與性質，實現(xiàn)數(shù)列求和的轉化與應用，綜合性強，融合度高.

四、數(shù)列與解三角形的交匯

例4已知△ABC的三邊長a，b，c成等差數(shù)列，且滿足a2+b2+c2=63，則邊長b的取值范圍是____.

分析利用等差數(shù)列引入公差參數(shù)d，結合條件建立涉及b與d的方程，根據(jù)參數(shù)d的取值情況來確定b的最大值，再結合三角形與不等式性質來確定b的最小值.

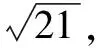
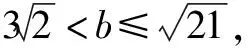
點評綜合等差數(shù)列、解三角形、平面幾何、不等式等眾多知識，實現(xiàn)數(shù)學知識、思想方法和能力的融合與交匯.

五、數(shù)列與數(shù)學文化的交匯

例5 (2019·麗水模擬)中國古代數(shù)學名著《九章算術》中有這樣一個問題：今有牛、馬、羊食人苗，苗主責之粟五斗.羊的主人說：“我羊食半馬.”馬的主人說：“我馬食半牛.”今欲衰償之，問各出幾何？以上問題的翻譯如下：現(xiàn)有牛、馬、羊吃了別人家的禾苗，禾苗的主人要求牛、馬、羊的主人共賠償5斗粟的損失.羊的主人說：“我的羊所吃的禾苗數(shù)量是馬的一半.”馬的主人說：“我的馬所吃的禾苗數(shù)量是牛的一半.”若按此條件賠償5斗粟的損失，那么牛、馬、羊的主人各應賠償多少斗粟？若牛、馬、羊的主人各應償還粟a升，b升，c升，其中1斗為10升，則下列判斷正確的是( ).

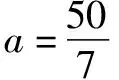
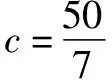
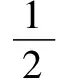
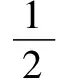
分析本題以《九章算術》為背景考查我國優(yōu)秀的傳統(tǒng)文化，意在考查考生的閱讀理解能力和解決實際問題的能力.通過閱讀，轉化為相應的等比數(shù)列問題，再利用等比數(shù)列的知識來分析與處理.

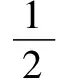
點評融合數(shù)學文化背景，結合數(shù)列的相關知識來抽象、建模、應用、綜合.

知識點間的融合是知識的進一步深化與拓展，是高考命題倡導的一個方向，要引起高度重視.平時教學與學習時，要重視課本，重視基礎，強調應用，倡導綜合，提升能力，提高品質.