利用建系解決多邊形與向量有關(guān)的平面問(wèn)題

趙靜敏

(山西省太原市山西大學(xué)附屬中學(xué)校 030006)

隨著多學(xué)科的交叉融合，向量不僅是高考必考的知識(shí)點(diǎn)，更是研究其他問(wèn)題的一種工具.而對(duì)于向量自身來(lái)說(shuō)，一般就兩種方法，一是利用基底，二是利用坐標(biāo).而涉及到坐標(biāo)就必然和建系相關(guān).

一說(shuō)到建系，我們首先想到的就是立體幾何中利用建系求面面角，線面角等；另外，我們?cè)趯W(xué)函數(shù)模型的建立和檢驗(yàn)時(shí)也用到了建系；在求曲線方程時(shí)也用到了建系，比如橢圓，雙曲線，拋物線方程的建立等.當(dāng)然，還有其他的建系方法.本文將對(duì)多邊形與向量有關(guān)的且可以利用建系來(lái)處理的一類(lèi)題型做一個(gè)簡(jiǎn)單分析.

一、較簡(jiǎn)單的與向量有關(guān)的建系

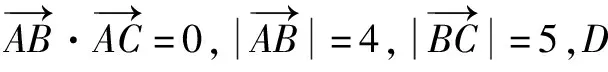
解法1利用基底。

解法2利用建系.

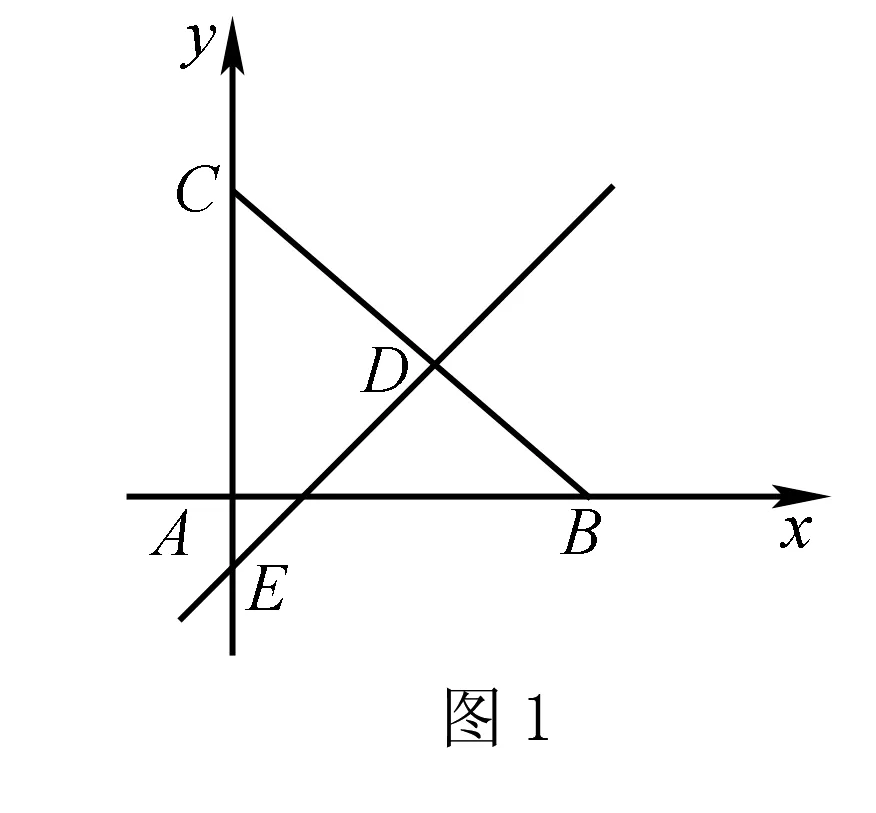
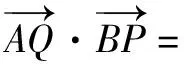
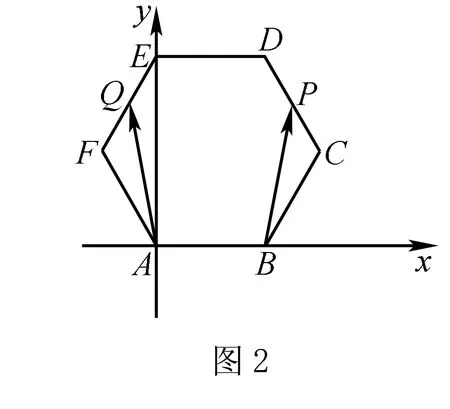
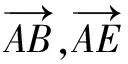
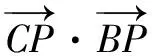
C.4 D.-1

二、較綜合的與向量有關(guān)的建系

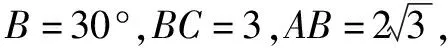
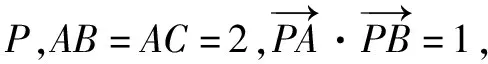
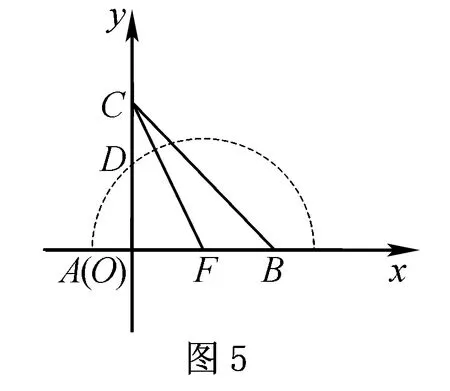
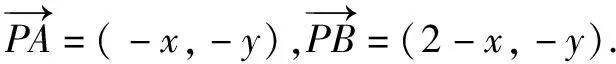
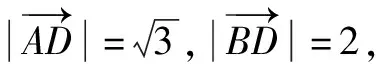
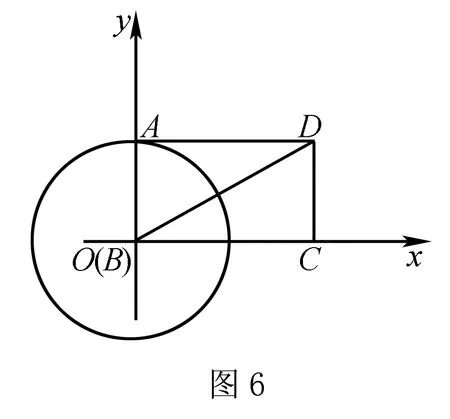
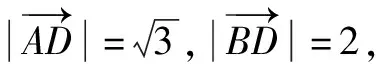
故選B.

涉及到多邊形與向量融合的問(wèn)題，建系相對(duì)簡(jiǎn)便一些.多個(gè)知識(shí)點(diǎn)的融合也對(duì)我們的能力提出了進(jìn)一步的要求.所以我們不僅要學(xué)，更要思.在打好打硬四基的基礎(chǔ)上，提高學(xué)生的核心素養(yǎng).