再現(xiàn)橢圓定義 滲透核心素養(yǎng)

李小蛟

(四川省成都市樹德中學 610091)

一、考題再現(xiàn)

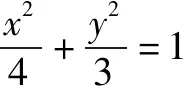
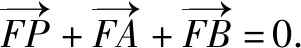
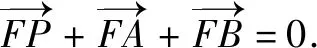
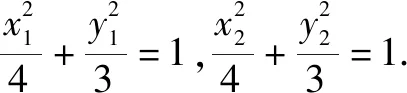
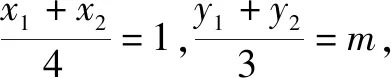
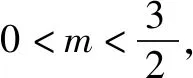
(2)由題意得F(1,0),設P(x3,y3),則(x3-1,y3)+(x1-1,y1)+(x2-1,y2)=(0,0).

由(1)及題設得x3=3-(x1+x2)=1,y3=-(y1+y2)=-2m<0.

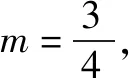
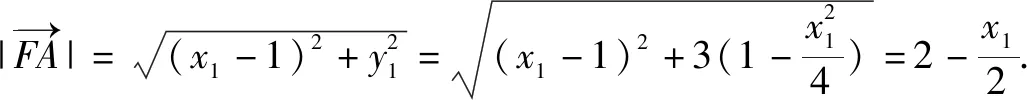
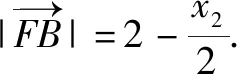
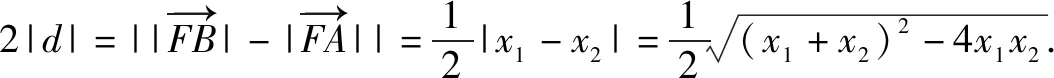
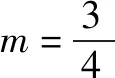
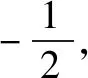
(1)求C的方程，并說明C是什么曲線.

(2)略.

即軌跡C為中心在坐標原點，焦點在x軸上的橢圓，不含左右頂點.

二、追本溯源

1.橢圓的第一定義

(1)

兩邊再次平方可得a2y2+(a2-c2)x2=a2(a2-c2)

(2)

兩邊同時除以a2(a2-c2)，

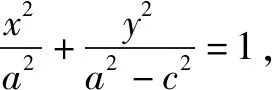
令b2=a2-c2，

2.橢圓的第二定義

平面上到定點距離與到定直線間距離之比為常數(shù)的點的集合(定點不在定直線上，該常數(shù)為小于1的正數(shù))，該定點為橢圓的焦點，該直線稱為橢圓相應焦點的準線.

這一定義又稱為圓錐曲線的統(tǒng)一定義，在我們現(xiàn)行教材人教A版選修2-1中沒有提出來，但有所呈現(xiàn).

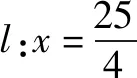
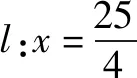
所以，點M的軌跡是長軸，短軸分別為10，6的橢圓.

3.橢圓的第三定義

平面內(nèi)的動點到兩定點A1(-a,0),A2(a,0)的斜率乘積等于常數(shù)e2-1的點的軌跡叫做橢圓.

這一定義也在我們現(xiàn)行教材人教A版選修2-1中同樣沒有提出來，但有所呈現(xiàn).

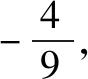
解析設點M(x,y)，∵(-5,0),(5,0)

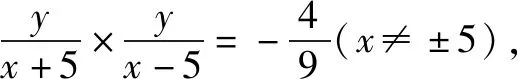
4.橢圓第二第義、第三定義的追本溯源

現(xiàn)行教材對橢圓的定義僅僅以第一定義的形式出現(xiàn)，第二定義、第三定義并沒有給出正式定義，只是在教材例題中有所呈現(xiàn).那么這三個定義之間是否有著必然的聯(lián)系與完全的統(tǒng)一呢，讓我們再從第一定義推導標準方程中去認真探究.

(3)

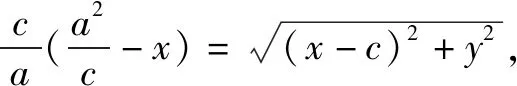
我們再看一下式a2y2+(a2-c2)x2=a2(a2-c2)，

移項可得a2y2=(a2-x2)(a2-c2)，

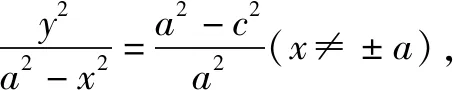
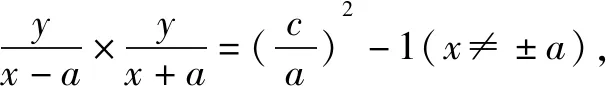
這即為橢圓的第三定義(平面內(nèi)的動點到兩定點A1(-a,0),A2(a,0)的斜率乘積等于常數(shù)e2-1的點的軌跡叫做橢圓).

三、遷移延伸

設A1(x1,y1),A2(x2,y2)為橢圓C上關(guān)于原點對稱的任意兩點，任取橢圓C上一點M(x,y)，若kMA1,kMA2均存在，則kMA1·kMA2=e2-1為定值.

分析∵A1,A2關(guān)于原點對稱，∴x1=-x2,y1=-y2

又∵A1(x1,y1),M(x,y)在橢圓上，

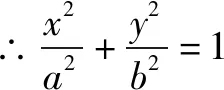
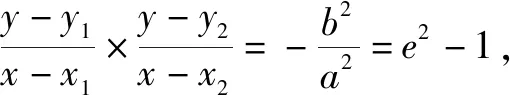
顯然橢圓第三定義實質(zhì)上是這一延伸結(jié)論的特例.

四、拓展應用

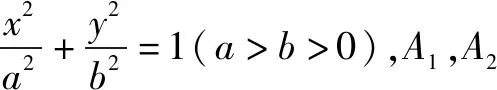
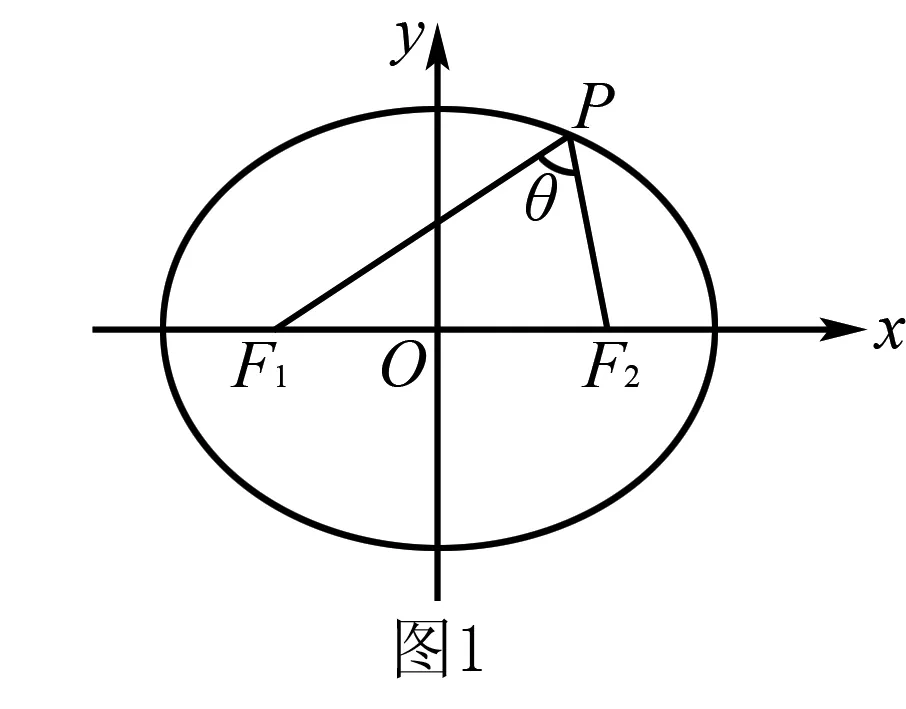
解析一解析幾何問題中求角三解形角度的最值，我們應選取這一角的某一三解函數(shù)值求解，由于正弦函數(shù)在(0,π)內(nèi)不單調(diào)，而余弦函數(shù)嚴格單調(diào)遞減.記∠F1PF2=θ,于是我們求解θ的余弦值.

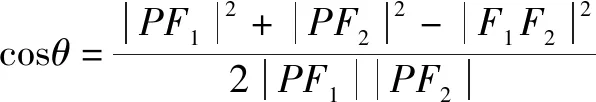
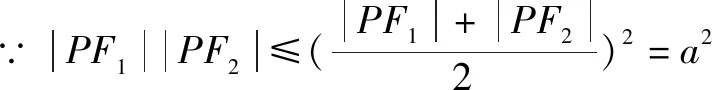
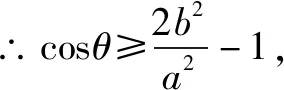
解析二接解析一

在2.4中根據(jù)橢圓第二定義我們得到了橢圓的右焦半徑公式|PF2|=a-ex，同理可行左焦半徑公式|PF1|=a+ex.

根據(jù)題意，當x=0，即P為短軸上的頂點時，cosθ取得最大值，θ取得最小值，得證.

解析三本問題還可運用橢圓焦點三解形的面積公式求證.

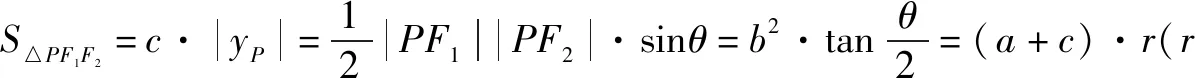
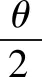
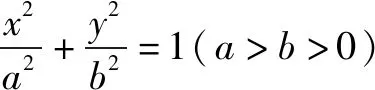
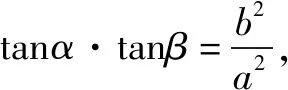
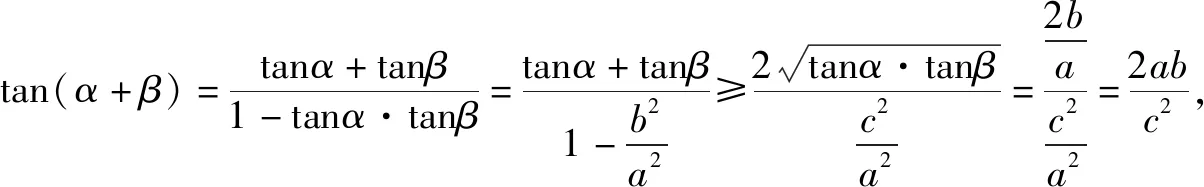
橢圓三個定義相互依存，相互聯(lián)系，對橢圓三個定義的再現(xiàn)過程實質(zhì)是就是學習解析幾何用坐標來理解圖形，對其相互聯(lián)系的呈現(xiàn)既有解析幾何運算的處理，也有轉(zhuǎn)化與化歸、數(shù)形結(jié)合等數(shù)學思想方法的體現(xiàn)，更重要的是在定義的推導，聯(lián)系、運用、延伸、拓展中對數(shù)學抽象、邏輯推理、數(shù)據(jù)處理、數(shù)學運算等核心素養(yǎng)的滲透和發(fā)展.