一道高考壓軸題引發(fā)的圓錐曲線定點問題探究

胡貴平

(甘肅省白銀市第一中學 730900)

解析幾何中證明直線過定點，一般是選擇參數表示直線方程、數量積、比例關系等，根據等式的恒成立、數式變換，通過推理、計算，找出參數之間的關系，并消去部分參數，將直線方程化為點斜式方程，從而得到直線所過的定點.當定點具備一定的限制條件時，可先探索出定點，再證明該定點與變量無關.

一、試題呈現

(1)求C的方程；

(2)點M，N在C上，且AM⊥AN，AD⊥MN，D為垂足.證明：存在定點Q，使得|DQ|為定值.

本題綜合考查直觀想象、邏輯推理、數學運算等數學核心素，考查了橢圓的標準方程和性質，圓錐曲線中的定點定值問題.

二、試題解析

(x1-2)(x2-2)+(y1-1)(y2-1)=0

①

當直線MN的斜率存在時，設方程為y=kx+m,如圖1.

代入橢圓方程消去y并整理,得

(1+2k2)x2+4kmx+2m2-6=0，

②

根據y1=kx1+m,y2=kx2+m,

代入①整理，可得

(k2+1)x1x2+(km-k-2)(x1+x2)+(m-1)2+4=0

將②代入，

整理化簡得(2k+3m+1)(2k+m-1)=0，

因為A(2,1)不在直線MN上，所以2k+m-1≠0，

當直線MN的斜率不存在時，可得N(x1,-y1)，如圖2.

①

三、引申探究

對于橢圓上一點作張角為直角所對的弦是否都過定點呢？

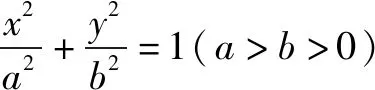
當直線MN的斜率存在時，設方程為y=kx+m,

②

根據y1=kx1+m,y2=kx2+m,代入①整理，

當直線MN的斜率不存在時，可得N(x1,-y1),

性質3 過拋物線y2=2px(p>0)上一點P(x0,y0)作兩條互相垂直的弦PM，PN，則直線MN恒過定點(2p+x0,-y0).

過圓錐曲線上一點P(x0,y0)作兩條直線互相垂直加強到兩條直線斜率之積是定值，是否仍然有張角所對的弦必過定點？

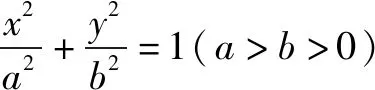
即d(x1-x0)(x2-x0)-(y1-y0)(y2-y0)=0,①

當直線MN的斜率存在時，設方程為y=kx+m,

②

根據y1=kx1+m,y2=kx2+m,代入①整理，

過圓錐曲線上一點P(x0,y0)作兩條直線斜率之積是定值，拓展到兩條直線斜率之和是定值，是否仍然有張角所對的弦必過定點？

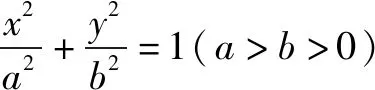
①

當直線MN的斜率存在時，設方程為y=kx+m,

②

根據y1=kx1+m,y2=kx2+m,代入①整理，

圓錐曲線上一定點P與另外兩點M，N的斜率之和或斜率之積為定值時，在斜率存在時，可設MN的方程y=kx+m與圓錐曲線方程聯立，根據斜率之和或斜率之積建立起參數k，m之間的關系(若是關于k，m之間是一元二次方程，要特別注意因式分解)，就可以得出直線過的定點，再在直線斜率不存在時單獨驗證.