基于多維連續時間馬爾科夫鏈的院感傳播及管控策略

蘇 強 ,朱 敏 ,祝延紅 ,鄒 妮

(1.同濟大學 經濟與管理學院,上海 200092;2.上海市第一人民醫院,上海 200080)

醫院感染(HI、NI或HAI,Hospital Infections、Nosocomial Infections or Healthcare-Associated-Infections,以下簡稱“院感”)是指住院患者或醫院工作人員在醫院內獲得的感染。隨著老年住院患者比重增加、侵入性醫療操作增多以及抗生素的濫用,醫院感染問題越發成為影響醫療服務質量的全球性醫學難題[1]。醫院感染的主要表現類型為多重耐藥菌(Multidrug-resistant Organisms,MDRO)感染[2],所謂的多重耐藥菌是指對臨床使用的3類或3類以上抗菌藥物同時呈現耐藥的細菌。根據全國醫院感染監測網數據顯示,患者因醫院感染導致人均住院日延長15.8 天,人均住院費用增加16 706元[3],這嚴重威脅患者生命并加重患者經濟負擔,同時消耗占用了寶貴稀缺的醫療資源。因此,如何有效預防和控制醫院感染成為醫院服務質量管理最困難、最迫切需要解決的問題之一。

利用數學模型研究醫院感染影響因素、傳播機制、演化規律及控制措施是目前的研究熱點[4]。目前國內外對于院感問題的研究大多基于臨床統計數據建立統計分析模型識別關鍵影響因素并評估其重要性。Amin等[5]及Adrie等[6]通過橫截面研究方法,拓展統計學模型識別易感人群并篩查院感的風險因素,最后對院感進行控制及預警。這一類研究主要為回顧性方法,只停留在風險因素識別,缺少對院感前瞻性研究,以及對傳播關鍵因素影響的定量刻畫。

近年來,對傳染病動力學的深入研究[7-8]為醫院感染研究提供了新的思路、理論和方法。Wang等[9]根據院感傳播性質量化傳播環節各參數構建院感傳播模型,計算模型在各情景下的平穩分布,驗證不同院感管控措施的有效性,結果顯示,相對于其他管控措施,對入院感染病人提早隔離最為有效。Wolkewitz等[11]不僅將醫護人員手部作為傳播路徑外,還考慮到感染病人周圍設備及器械污染所導致的感染傳播,仿真結果表明,需要對感染病人的設備做好專人專用,防止交叉感染。Wang等[12]則根據ICU 病房內護工人群,將醫護人員分為兩類人群(護工及護士),并根據兩類人群的工作性質設定不同參數拓展S-I模型,研究護工對于感染傳播的影響,結果發現,除了改善手部衛生之外,聘用經過適當訓練的護工可以減少病房中 MDRO 感染。Ruhang等[13]及馮丹丹等[14]主要考慮患者間直接傳播及醫患間間接傳播,并結合傳染病倉室模型,計算傳播過程穩定平衡點,模擬不同情景下人群狀態演變過程并確定感染爆發閾值,最后通過數值模擬驗證了結論的正確性。這一類研究雖然量化了傳播路徑上的關鍵因素,但是倉室模型簡單地將感染個體群體化,未能綜合考慮個體(病人及醫護人員)感染狀態轉移差異。另外,倉室模型在模擬病人狀態演變時,忽略了人群的有效接觸,重復計算接觸感染次數,高估了感染風險[15]。

院感(以MDRO 病原菌感染為例)傳播主要有兩個特點:①隨機性。相對于社會人群,病人數較少且不同狀態個體接觸感染差異性、隨機性較高。②媒介傳播。病房中醫護人員在傳播過程中充當媒介作用,病原菌在病人與醫護人員之間雙向傳播。多維連續時間馬爾可夫鏈(Multidimensional Continuous-time Markov Chain,MCTMC)可以模擬兩個及以上獨立個體的狀態演變過程,從離散個體角度建模分析疾病在連續時間維度上的隨機傳播過程,突破了倉室模型中群體一般性的局限。

基于此,本文以連續時間馬爾可夫鏈為主要研究框架,將感染媒介(醫護人員)集成到SIS傳播機制,構建MCTMC-SIS 傳播模型,并與倉室模型中狀態演變過程進行對比,證明模型的先進性。通過計算平穩狀態下各狀態的期望值,分析個體感染狀態的演化規律。最后,通過數值模擬,對各參數的重要性進行評估,并對各情景下的院感控制給予管控策略的建議。

1 院感模型設計

根據院感傳播特點,醫護人員(Health-Care Workers,HCWs)手部污染及不當的醫療操作,是造成院感傳播的主要原因[16]。因此,醫護人員成為院感傳播過程中的傳染媒介。ICU 患者一方面具有病情嚴重、伴有多種基礎疾病、集體免疫力差等特點;另一方面,患者多進行侵入性器械操作及廣泛使用抗生素,這些極大地增加了患者感染的風險。本文以ICU 科室為例進行建模分析,考慮由于病人入院攜帶病原菌,通過醫護人員不恰當護理及操作的傳播路徑,產生醫院感染傳播的現象。根據院感傳播路徑圖(見圖1),此類傳播過程類似SIS(Susceptible-Infected-Susceptible)傳播。在SIS傳播機制中,病人分為易感與感染兩類群體,其中易感狀態病人會以一定概率成為感染狀態。

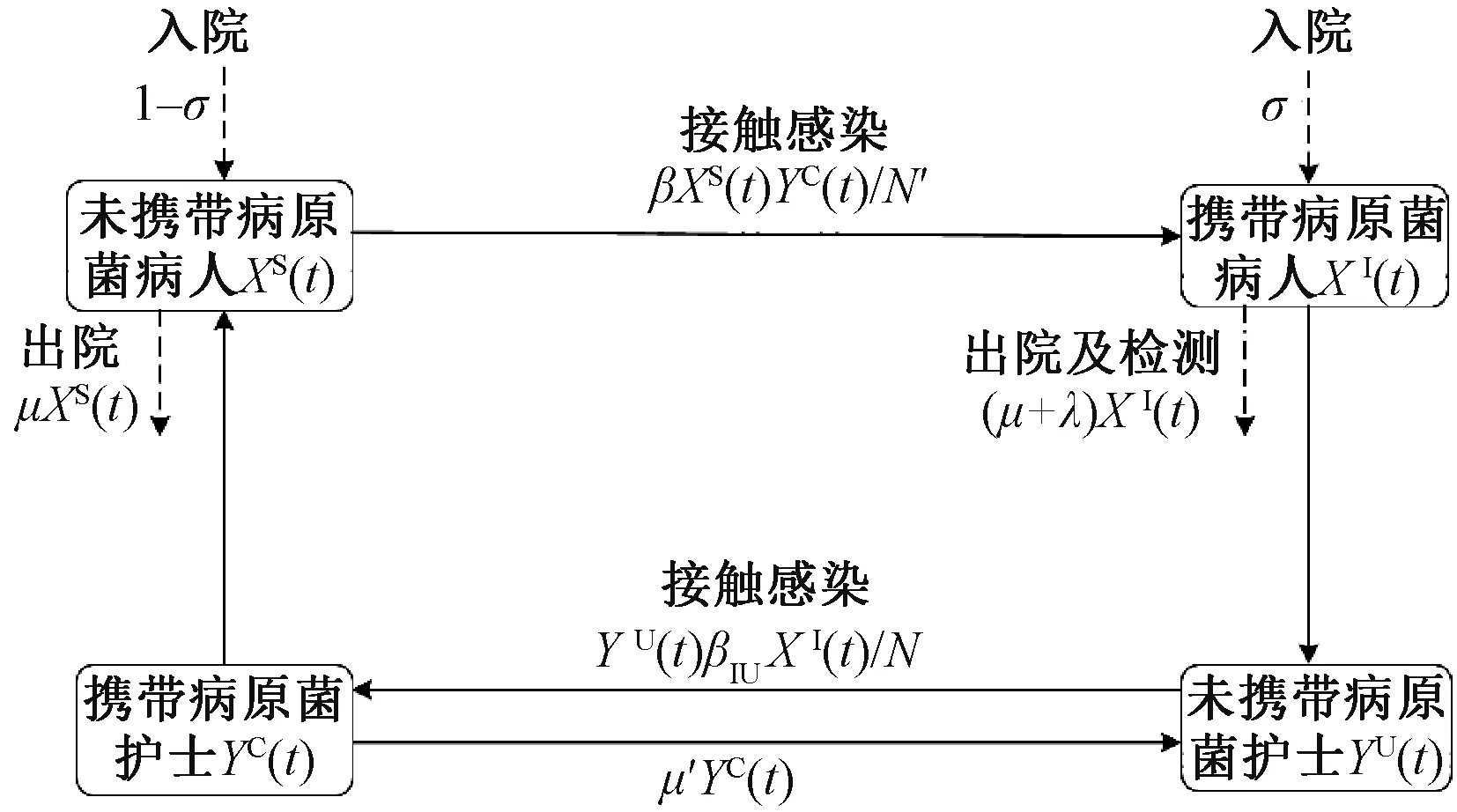
圖1 醫院感染傳播路徑圖

1.1 參數說明

為保證ICU 科室人數為一定值,當感染病人治愈出院或監測隔離,會有相同數量易感病人入院。在病房中,主要有如下事件導致院感傳播:病人出入院、感染監測和HCWs護理等。

(1)病人入院時以σ概率攜帶病原菌,定義t時刻這部分病人為感染狀態或以一定概率成為感染狀態,數量為XI(t);同時,病人以(1-σ)概率未攜帶病原菌,定義t時刻這部分病人為易感狀態,數量為XS(t),即XI(t)+XS(t)=N,其中,N為病房病人數總人數。

(2)病人以出院率μ離開,感染狀態病人會以監測率γ檢查隔離,故單位時間(天)內易感及感染狀態病人離開病房的人數分別為μXS(t)和(μ+γ)XI(t)。

(3)醫護人員(HCWs)在與病人護理接觸過程中,由于消毒或器械使用不當成為病菌攜帶者,定義t時刻攜帶病原菌的HCWs數量為YC(t)(受污染狀態),未攜帶病原菌的HCWs數量為YU(t)(未受污染狀態),其中,YC(t)+YU(t)=N',N'為病房醫護人員總人數。βIU為病人與HCWs接觸感染發生率,β為HCWs與病人接觸感染發生率,μ'為醫護人員手部消毒頻次,故單位時間內受污染狀態的HCWs的數量增加βIUYU(t)XI(t)/N,減 少μ'YC(t)。同理,由于護理不當,受污染狀態的HCWs會接觸易感狀態病人,使其成為感染狀態,故單位時間增加數量為βYC(t)XS(t)/N'。

1.2 模型假設

為便于模型構建做出如下假設:

(1)病房內病人及HCWs數量為一定值(病人數為N,HCWs數量為N')。在單位時間內,病人因出院或監測攜帶病原菌被隔離,會有相同數量病人入院,且病人是完全隨機均勻混合在一起。

(2)無窮小時間下,有且僅有一種狀態發生改變,且不同人群狀態數量變化相互獨立,即當t→0時:

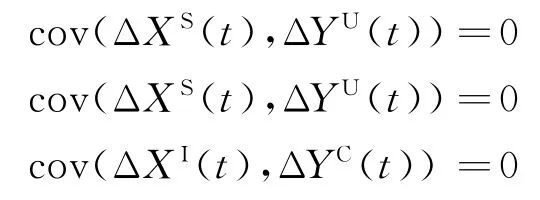
(3)病房內病原菌感染傳播只考慮HCWs的媒介傳播,忽略病人與病人之間的直接傳播,且醫護人員與病人之間相互接觸時,病原菌接觸感染發生率相等,即β=βIU。

(4)一旦病人被監測到攜帶病原菌將立即隔離(即切斷感染源,對系統中病原菌傳播不產生任何影響);HCWs每次手部消毒可完全消除病原菌。

1.3 模型構建

1.3.1 倉室模型 根據傳染病動力學及上述分析,構建如下SIS倉室模型[4-5,17]:

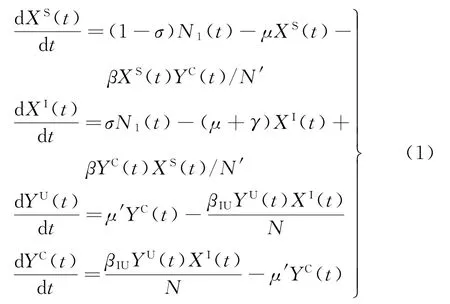
式中,N1(t)為t時刻病人出院及監測隔離離開病房的人數,N1(t)=μXS(t)+(μ+γ)XI(t)。此類模型存在如下不足:μXS(t)為t時刻易感狀態病人出院人數;μXI(t)為t時刻感染狀態病人未被監測而出院的人數。當μXI(t)人群離開病房時,根據模型假設會有σμXI(t)攜帶病原菌病人入院。然而,相較于病人入院前,σμXI(t)感染群體對病房系統中新增感染不產生任何影響,只有σμXS(t)感染群體新增系統感染病人數量,增加接觸感染數。因此,此類模型將μXS(t)與μXI(t)兩類群體混淆在一起,未能考慮到出院病人狀態差異,重復計算接觸感染次數。因此,針對上述不足,本文對此模型進行了拓展。

1.3.2 MCTMC-SIS模型 病原菌在病房傳播過程中,個體狀態是在連續時間下離散變化的。由于在院感傳播中病人及醫護人員是不同演變狀態的個體(見圖1),故進一步引入多維連續時間馬爾可夫鏈(MCTMC)建立MCTMC-SIS模型。

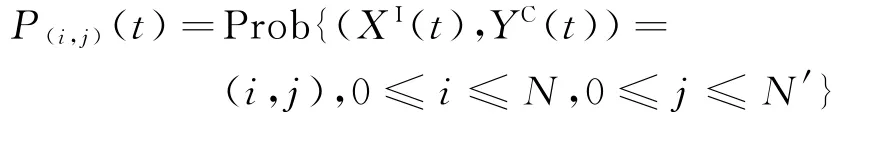
傳播過程主要依賴二維離散隨機變量(XI(t),YC(t))及聯合概率函數P(t)=(P(0,0)(t),…,P(N,N'))。其中,表示二維變量(XI(t),YC(t))在t時刻處于(i,j)狀態的概率。由于P(i,j)(t)大小與時間t有關,故定義單位時間內概率的變化為轉移速率。根據圖1計算各狀態下的轉移速率,如表1所示。

表1 MCTMC-SIS模型狀態轉移速率表

根據表1可得(i,j)時間間隔Δt下各狀態的轉移概率[18],用于模擬院感傳播過程中個體狀態的演化規律。其中:

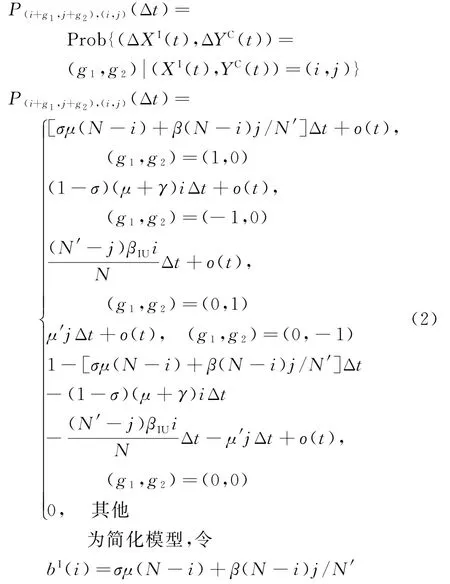
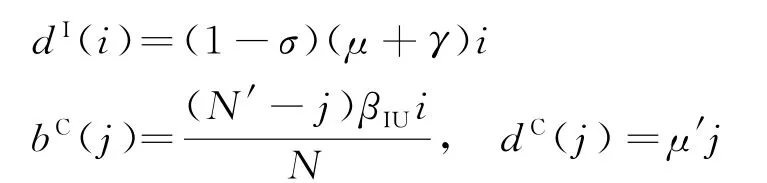
根據式(2)及Kolmogorov微分方程[19],求得二維變量(XI(t),YC(t))在(t+Δt)時刻處于(i,j)狀態的概率為

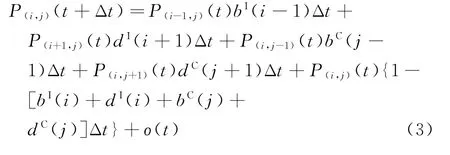
2 院感模型分析與計算

2.1 兩類模型狀態演變率分析對比

本節主要通過計算MCTMC-SIS模型t時刻下各狀態概率,求解得到各狀態期望值變化率并與倉室模型中狀態演變率進行比較(以XI(t)狀態轉變為例),從而對比不同模型下的感染風險,論證MCTMC-SIS模型的先進性。令t時刻攜帶病原菌病人數量XI(t)的期望值為

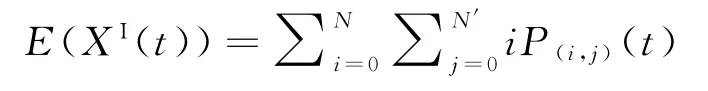
即根據式(3)可得(t+Δt)時刻XI(t)的期望值:

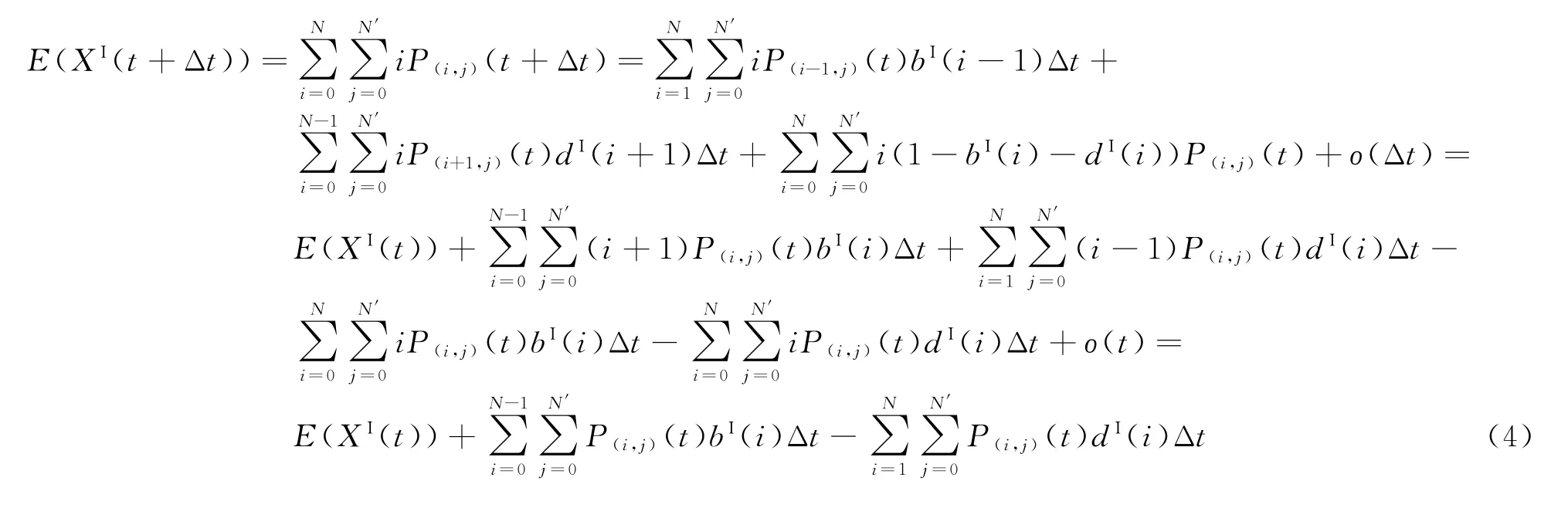
等式兩邊減去E(XI(t)),得

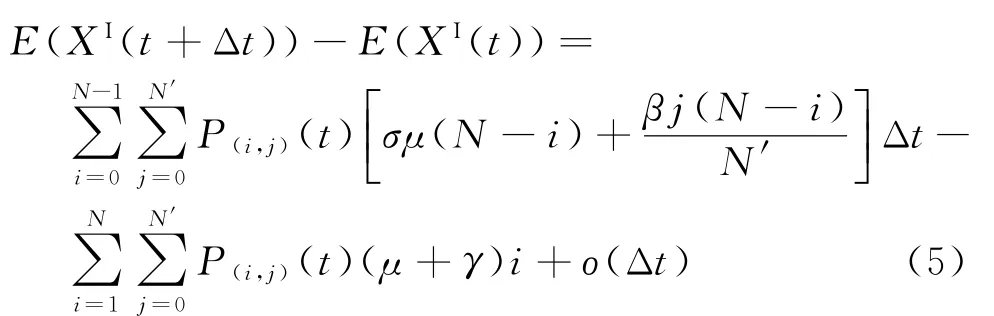
等式兩邊同時除Δt并令Δt→0,得

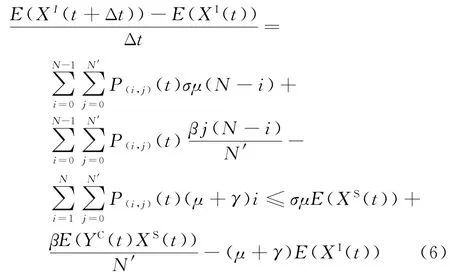
又因為隨機變量YC(t)、XS(t)相互獨立,即E(YC(t)XS(t))=E(XS(t))E(YC(t)),所以式(6)可轉化為

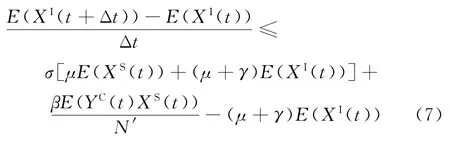
式(7)的右側與式(1)中XI(t)的微分等式相同,其中,N1(t)=μXS(t)+(μ +γ)XI(t)被[μE(XS(t))+(μ+γ)E(XI(t))]代替、YC(t)被E(YC(t))代替、XS(t)被E(XS(t))代替、XI(t)被E(XI(t))代替。因此,得到MCTMC-SIS模型中的隨機變量XI(t)均值小于倉室模型微分方程中XI(t)的解。

這充分證明,由于倉室模型未能區分個體狀態而導致重復計算接觸感染數,從而高估了醫院感染風險。相對于倉室模型,MCTMC-SIS模型區分個體狀態,記錄院感傳播過程中醫護人員與病人之間的有效接觸,模型具有先進性。因此,MCTMC-SIS模型較合適構建院感傳播過程。

2.2 MCTMC-SIS模型平穩狀態計算

記隨機變量Tij為隨機變量(XI(t),YC(t))停留在(i,j)狀態的時間,Hij(t)為大于t的概率,即Hij(t)=P(Tij≥t)。根據式(2)可得

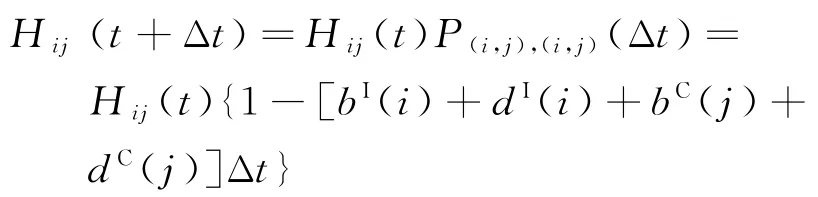
對t求導,可得

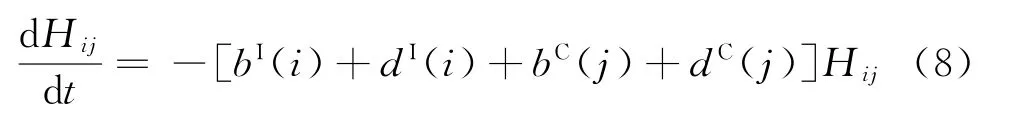
又因為Hij(t)=0,所以

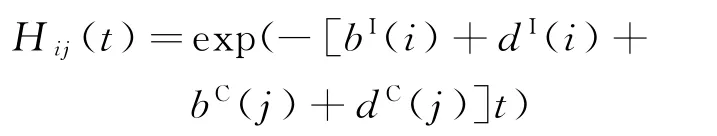
即Tij服從參數為[bI(i)+dI(i)+bC(j)+dC(j)]的指數分布,因此,Tij的分布函數

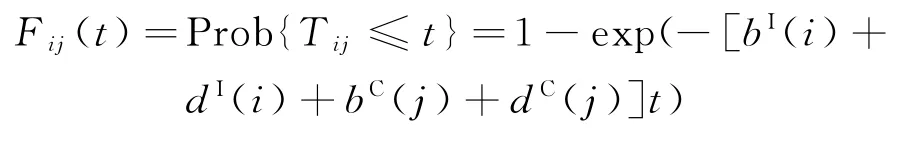
令隨機變量U服從(0,1)的均勻分布,即

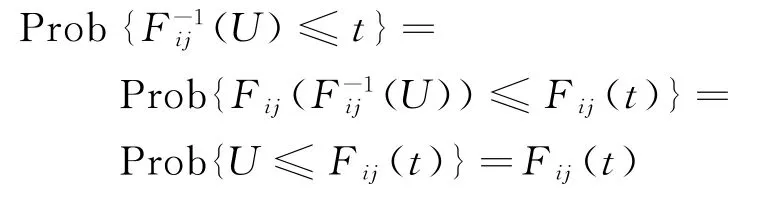
即

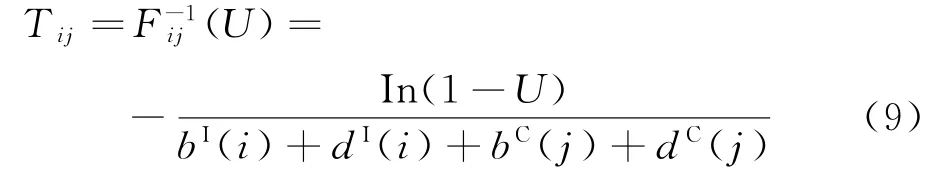
由式(9)可得在院感傳播中時間步長Tij不僅與隨機變量(XI(t),YC(t))狀態相關,還與服從(0,1)均勻分布變量U相關,故t時刻的狀態變量(XI(t),YC(t))數值不定,本文將對其平穩狀態進行分析。

步驟1平穩狀態定義。

當院感傳播處于平穩狀態時,二維離散隨機變量(XI(t),YC(t))為一定值。即當t→∞時,(XI(t+Δt),YC(t+Δt))=

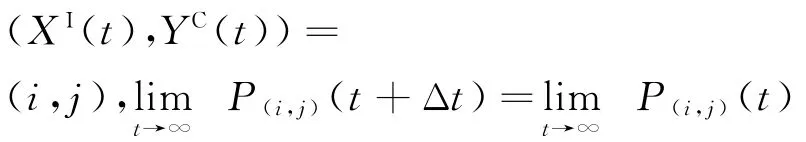
此時將式(3)兩邊同時減去P(i,j)(t)并令Δt→0,得

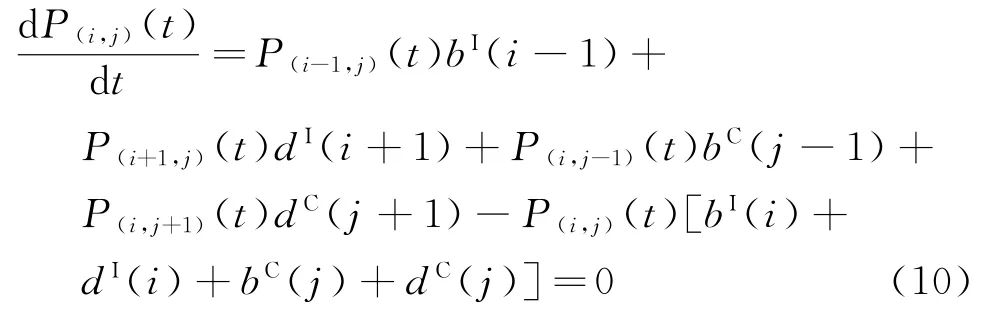
步驟2Q矩陣定義。

當0≤i≤N,0≤j≤N'時,式(10)可進一步表示為矩陣表達式:

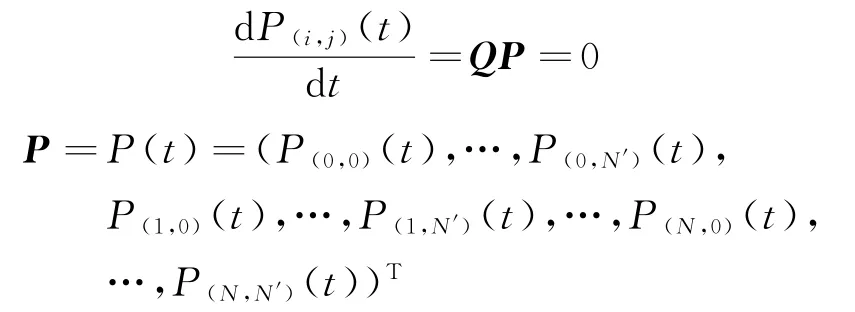
其中:向量P的維度為(N+1)×(N'+1);Q為狀態轉移速率矩陣[20],Q的維度為

表達式為

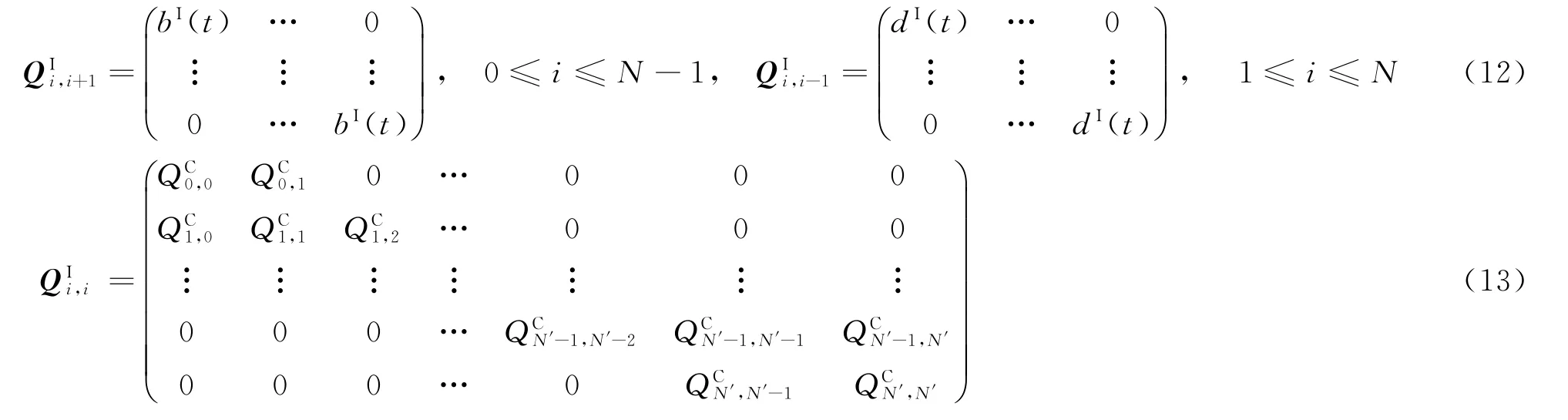
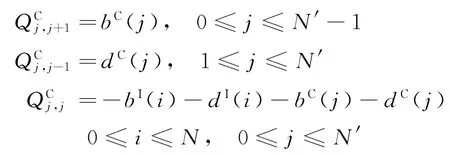
步驟3平穩狀態下向量P求解。

根據式(8)及P向量的定義,得到下式關于P向量的線性方程組,求得轉移過程中平穩狀態下P向量的值,

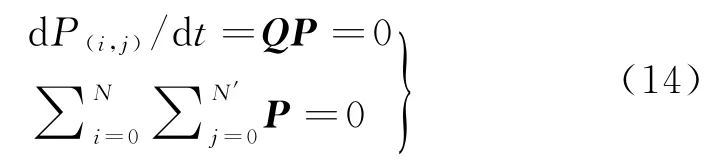
即可得各人群平穩狀態下數量期望值為:

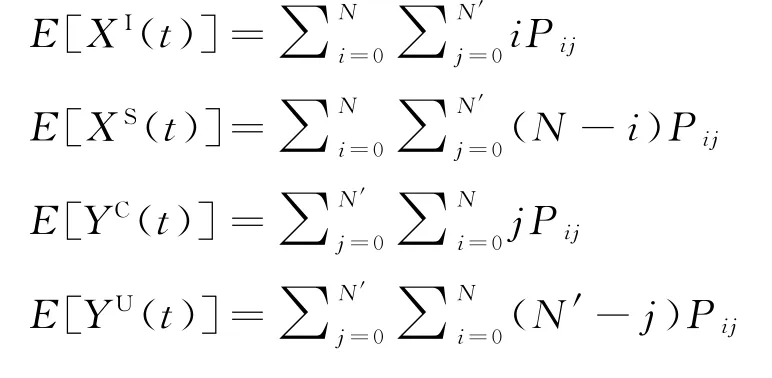
3 數值仿真

本文以上海第一人民醫院(南院)ICU 科室為例,該科室共有40病床數,6名專有護士。新入院病人攜帶病原菌的比例σ=0.05,病人出院率μ=0.06,病人監測率γ=0.2,護士每天平均洗手頻次為14,最高洗手頻次為20,其他參數選自文獻[21]。ICU 中傳播參數初始值如表2所示。

表2 ICU中傳播參數初始值

3.1 靈敏度分析

根據表2參數并結合假設2,在Inter(R)Core(TM)i7-7500U CPU@2.70 GHz 的PC上使用MATLAB軟件,以隨機變量

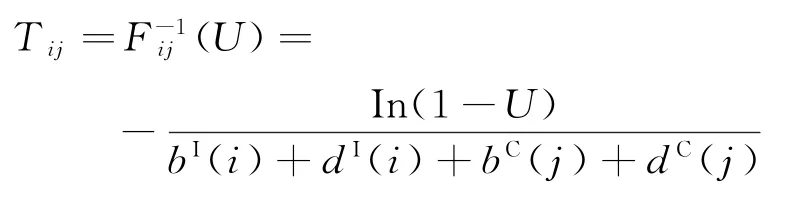
作為步長模擬各狀態人群數量演變1 000次,并取平均數。如圖2所示,初始值設為(XI(0),YC(0))=(2,1)。經過130 步長后,院感傳播處于平穩狀態(XI(t),YC(t))=(8,1)。

圖2 病人及醫護人員各狀態數量演變(初始值XI(0)=2,YC(0)=1)

下面根據式(14)求解MCTMC-SIS模型P向量中各Pij值,并計算各平穩狀態人數期望值。通過數值實驗對各參數進行靈敏度分析,評估并驗證管控措施的有效性。定義平穩分布時各病人狀態(感染或易感)的比例分別為P(XI)和P(XS),醫護人員狀態(受污染或未受污染)的比例分別為P(YC)和P(YU)。由于

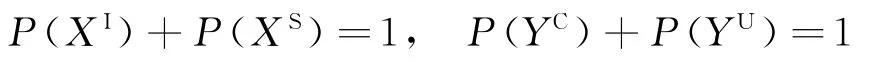
故取P(XI)和P(YC)作為院感傳播分析指標,表達式為:

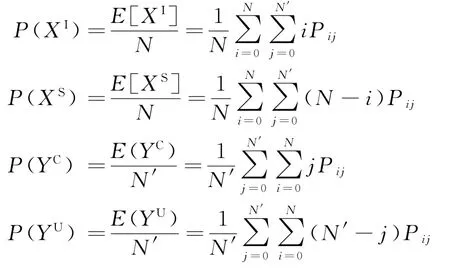
圖3所示為評估病人與醫護人員之間接觸感染發生率對于院感傳播的影響。當傳播率β從0.05增加至0.5時,感染病人的比例從5%增加至55%,攜帶病原菌的醫護人員比例從3%增加至60%,故在醫護人員日常護理中需降低接觸傳播率,減少病人感染的風險。目前,醫護人員降低接觸傳播率的措施最常見的是:提高洗手頻率、防護衣及手套一人一用以及專有護士護理等[16]。

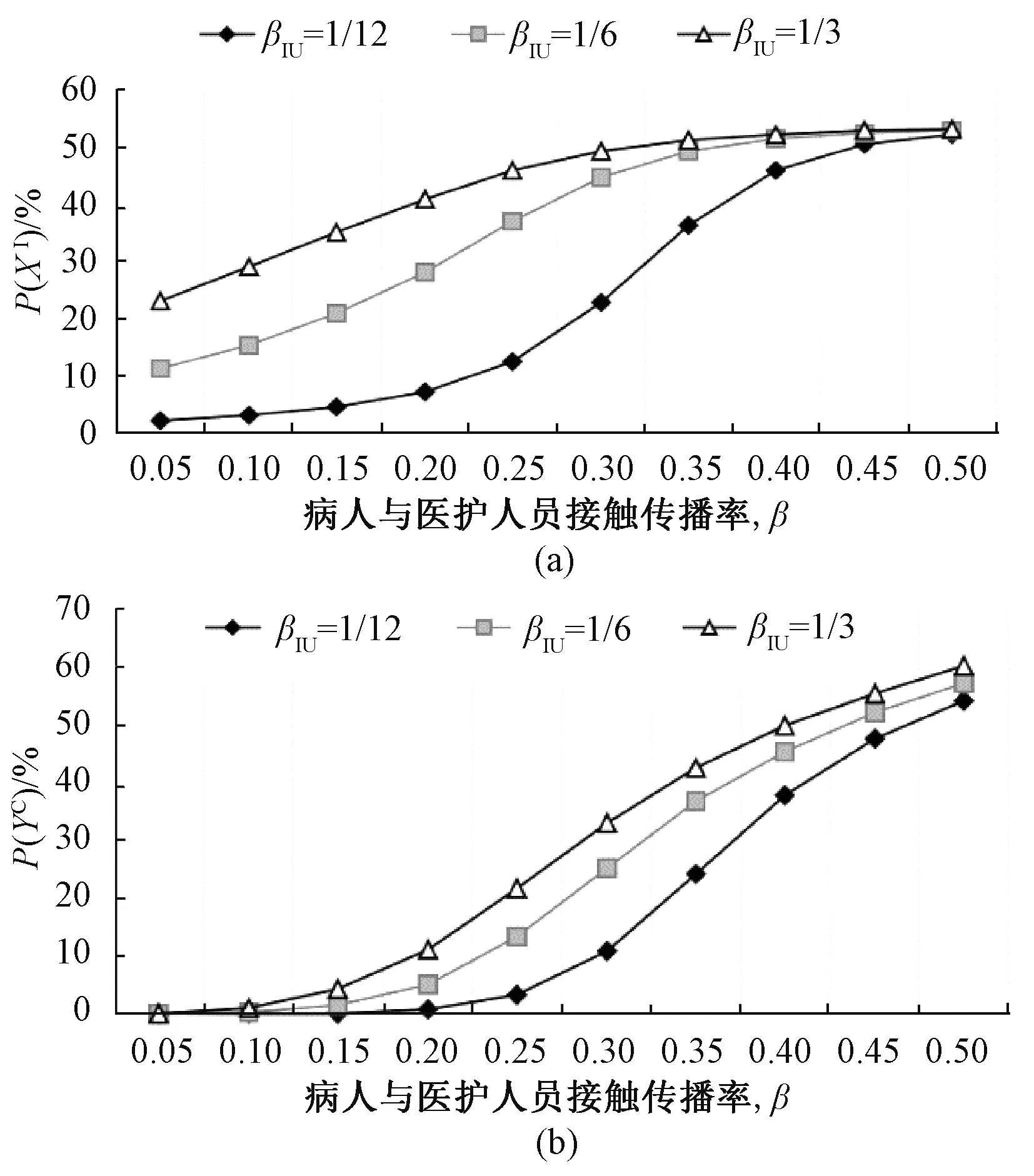
圖3 病人及醫護人員狀態相對接觸傳播率的變化

圖4所示為評估醫護人員洗手頻率(洗手頻率(依從性)=每天平均洗手次數/每天最高洗手次數,本文取20)及入院病菌攜帶率對院感傳播的影響。由圖4(b)可見,當醫護人員洗手頻率從0.25提高至0.7時,醫護人員成為病菌攜帶者的比例從50%降低至5%以下。由圖4(a)可見,當病菌攜帶概率值較低(σ≤0.05)時,提高洗手頻率降低醫護人員成為污染者的概率,從而減少感染病人的概率;當σ=0.01時,醫護人員洗手頻率從0.25提高至0.85,感染病人比例從50%降低至3%;然而,當σ較高(如0.1)時,無論醫護人員洗手頻率多高,都無法降低感染病人比例。這主要是因為提高洗手頻率只能降低醫護人員攜帶病菌概率,減少醫護人員與病人接觸感染數,但是無法降低σ值。病人入院攜帶的病菌是整個病房院感傳播的傳染源,對于病房系統感染傳播影響最大,所以病人入院病菌攜帶率是院感傳播控制的重要指標。

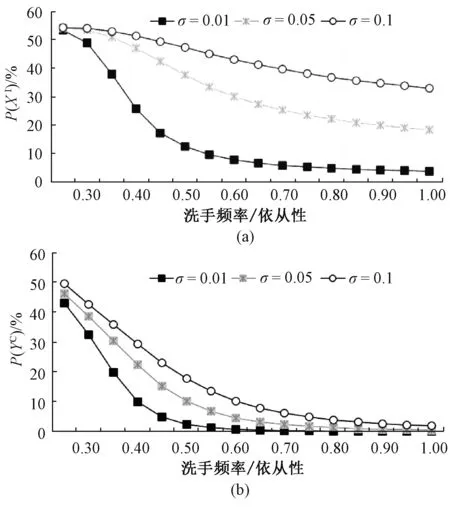
圖4 病人及醫護人員狀態相對洗手頻率及病菌攜帶率變化

圖5所示為評估感染病人監測率對院感傳播的影響,感染病人監測一方面是病人入院時的監測,監測其是否感染或攜帶病原菌;另一方面是對住院感染病人的監測。由圖5(a)可見,無論σ取值多少,當監測率γ從0.05提高至0.7時,感染病人的比例從50%降低至10%以內,故對于入院攜帶病原菌的病人或感染的病人,要早預防、早發現、早隔離。當病人住院時長增加時,病人感染風險增大,故提高病人出院率,有利于降低病人感染風險。

圖5 病人及醫護人員狀態相對監測率及病菌攜帶率變化

圖6所示為評估病人出院率對院感傳播的影響。由圖6(b)可見,當σ較小(取0.01)時,病人出院率從0.05提高至0.4時,感染病人從40%降低至10%;當σ較高(≥0.05)時,提高病人出院率對于降低感染病人比例影響較小。這主要是因為當病人攜帶病原菌比例較高時,提高病人出院率導致病房系統人員“大進大出”,系統病原菌增多,院感傳播可能性增加。病人出院的同時存在感染風險的病人入院,并沒有降低系統的感染傳播風險。

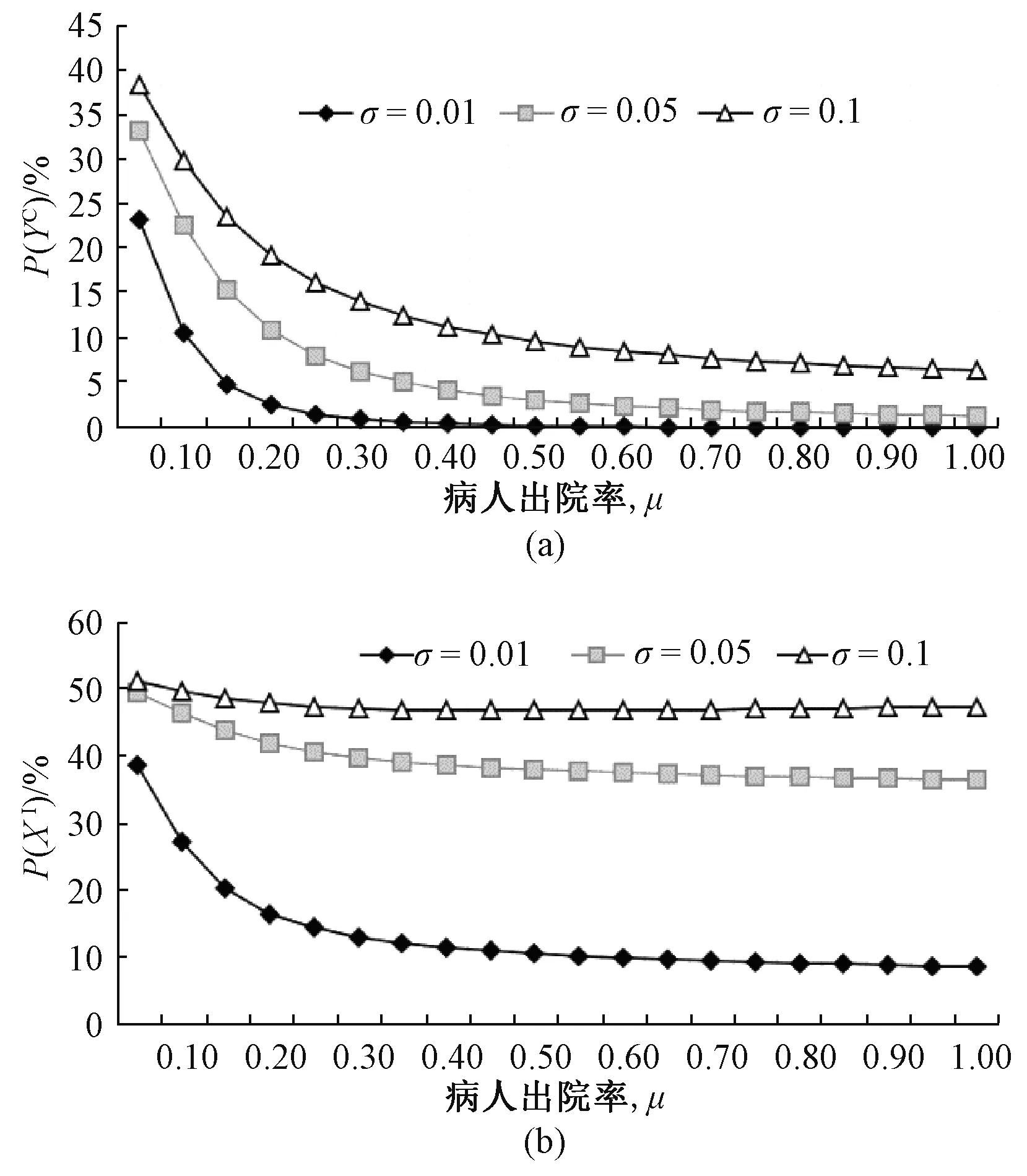
圖6 病人及醫護人員狀態相對出院率及病菌攜帶率的變化

通過調整傳播參數,驗證實際院感管控措施的有效性。結果發現,病人入院攜帶病原菌概率是影響院感傳播的重要參數。當入院攜帶病原菌概率較低(<0.05)時,提高醫護人員洗手頻率及出院率,可以有效降低感染風險。對于攜帶病菌病人或感染病人,需要做到早預防、早發現、早隔離。其中有效的管控措施主要有:①病人入院。監測病人是否感染或攜帶病原菌。②病人住院。提高醫護人員的洗手頻率(≥0.7),降低接觸傳播率,提高存在感染風險病人的監測率(≥0.7)。③病人出院。提高病人出院率,重點看護住院時間較長病人。

4 結語

倉室模型在構建院感傳播過程中未能區分出院病人狀態,導致重復計算接觸感染數,從而高估了系統感染風險。本文基于這一問題,以多維連續時間馬爾可夫鏈(MCTMC)為研究框架,精準刻畫病人及醫護人員的感染狀態及其演變過程。結合SIS傳播機制,構建MCTMC-SIS 傳播模型,從離散個體角度建模分析疾病在連續時間維度上的演變過程,突破了倉室模型中群體一般性的局限。最后,通過數值仿真驗證了實際護理策略的有效性,并評估傳播參數的重要性。結果顯示,病人攜帶病原菌概率對院感傳播影響較高。當入院病人攜帶病菌概率較高(≥0.05)時,提高病人出院率及醫護人員洗手頻率,無法有效降低醫院感染風險。在實際防控中需提早監測感染患者,降低病人感染風險。但是在院感傳播中存在多種病菌且感染前存在潛伏期,本文未考慮不同病原菌交互影響及病人潛伏期,與實際傳播存在一定的差距,這些將在后續工作中進一步討論。