針對高速機動目標的分數階滑模制導律

唐驍 葉繼坤

摘要：針對高速機動目標攔截問題，提出了一種基于分數階滑模控制理論的制導律設計方案。首先借助Fast Terminal滑模面設計思路，在Fast Terminal滑模動態面中引入視線角速率的分數階項，構建分數階動態滑模超平面，然后，結合分數階微積分理論，在分數階動態滑模超平面的基礎上推導出分數階滑模制導律，利用無窮狀態方法與Lyapunov穩定性理論證明了分數階滑模制導律的穩定性。仿真結果表明，該制導律可使導彈視線角速率在2 s內收斂，平均過載較小，且具有更高的制導精度，終端脫靶量在0.5 m以內。

關鍵詞： 制導律;分數階滑模;無窮狀態方法;有限時間收斂;高速機動目標;攔截

中圖分類號：TJ765; V448 ??文獻標識碼： A? 文章編號： 1673-5048（2021）02-0021-06

0 引? 言

近年來，彈道導彈和臨近空間高超聲速飛行器等高速機動目標威脅不斷涌現，其速度在馬赫數5以上，無固定彈道，能長時間大范圍持續機動，可對數千或上萬公里外的軍事目標實施全球打擊，給傳統的導彈攔截系統帶來了嚴峻的挑戰。學者采用了許多方法來研究針對高速機動目標攔截的導引律，主要有基于比例導引的制導律[1-3]，比例導引律（PNG）因其形式簡單，執行效率高而被廣泛研究和應用，如果目標無機動，PN制導律具有不錯的制導精度，但在有目標機動的情況下，其制導精度不高。文獻[4]提出了一種基于預測控制的三維微分對策制導律，能在目標機動的情況下滿足能量消耗和制導精度等性能指標，但計算過程復雜，需要信息較多。文獻[5]基于L2增益魯棒控制理論設計了L2增益制導律，可使視線角速率在有限時間內收斂到零，制導精度較高，但是沒有對能量消耗進行控制。文獻[6]針對攔截臨近空間高速機動目標，基于有限時間理論，設計了有限時間收斂制導律，能實現對目標直接碰撞攔截，但過載指令變化劇烈，對執行器要求較高。

隨著分數階微積分（Fractional order calculus，FOC）理論的發展，FOC的工程應用越來越廣泛[7-9]。不像整數階微分的不連續變化，FOC將傳統的整數階微積分的階次推廣到了非整數階，其反映的不再是點或者局部的性質，而是綜合考慮了歷史和全局分布式的信息[10]，具有記憶和時間依賴性的現象。FOC的主要優點是參數少，形式簡單，具有特殊記憶功能和穩定特性，在制導和控制領域得到了越來越多的應用。

文獻[11]設計了一種新的分數階張力控制律，用于控制空間繩系統的快速穩定。文獻[12]提出了一種求解分數階系統最優控制問題的方法。文獻[13]對不同的分數階超混沌系統的控制時間進行了分析。文獻[14]將FOC控制器應用于彈體姿態控制，其控制效果優于經典PID控制。文獻[15]結合FOC理論和PN制導律，提出了PDλ制導律，避免了PN制導律的缺點，有較高的制導精度和較短的攔截時間。文獻[16]針對機動目標攔截問題，設計了一種基于FOC理論的新型三維末制導律，制導精度高，攔截時間短，過載變化較為平穩，解決了傳統 PNG末端視線角速率發散導致的過載激增問題，但對于高速機動目標的攔截性能沒有研究。

在臨近空間高超聲速目標或者導彈類目標攔截中，常采用零化視線角速率和有限時間收斂理論設計制導律，這類制導律雖然攔截精度高，但過載變化劇烈，總能量消耗較大。為此，本文結合FOC和有限時間收斂理論提出分數階滑模制導律。經仿真驗證，分數階滑模面收斂性能優于整數階滑模面，使得過載變化平緩，能在目標機動的情況下輸出較小的過載，達到更高的制導精度且能量消耗更小。

1 預備知識

分數階微積分算子可以表示如下：

綜上所述，本文所設計的分數階滑模制導律能通過選取適合的參數，使得視線角速率在有限的時間內到達滑模面，并最終沿著滑模面收斂至零。

4 仿真分析

為驗證分數階滑模制導律（FOSMG）的有效性，在縱向平面內，目標采用圓弧機動和正弦機動兩種情形進行數值仿真，并與快速終端滑模制導律（FTSMG）和比例導引律（PNG）進行對比。

4.1 仿真條件

導彈的自動駕駛儀模型可表示為[19]

T=ω2n（τs+1）（s2+2εωns+ω2n） （38）

在此自動駕駛儀時間常數τ為0.5 s，阻尼常數ε取0.6，頻率ωn取18 rad/s。

首先定義仿真初始參數，攔截器與目標的初始位置為RM=[016 000]m和RT = [35 000 20 000] m。攔截器初始速度VM =1 500 m/s，初始速度方向角為20°，目標初始速度VT=1 800 m/s，初始速度方向角為180°。設目標機動方式已知，視線角速度由紅外導引頭獲取[20]，彈目相對速度和距離通過射頻制導雷達獲取。

制導律能量消耗性能指標選取如下：

J=∫Tend0a2M/Tend

制導律參數選取如表1所示。

4.2 目標圓弧機動

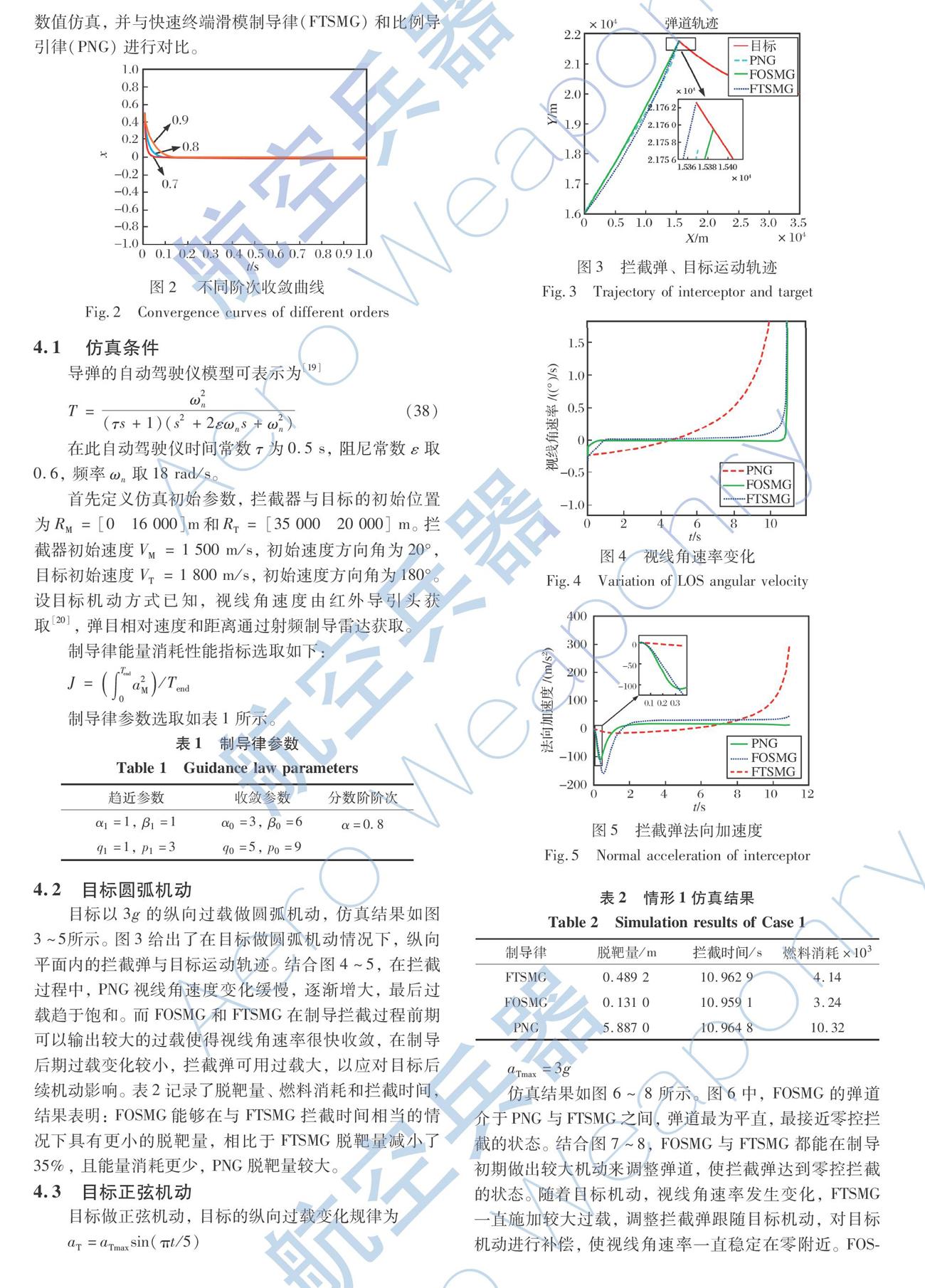
目標以3g的縱向過載做圓弧機動，仿真結果如圖3～5所示。

圖3給出了在目標做圓弧機動情況下，縱向平面內的攔截彈與目標運動軌跡。結合圖4～5，在攔截過程中，PNG視線角速度變化緩慢，逐漸增大，最后過載趨于飽和。而FOSMG和FTSMG在制導攔截過程前期可以輸出較大的過載使得視線角速率很快收斂，在制導后期過載變化較小，攔截彈可用過載大，以應對目標后續機動影響。 表2記錄了脫靶量、燃料消耗和攔截時間，結果表明：FOSMG能夠在與FTSMG攔截時間相當的情況下具有更小的脫靶量，相比于FTSMG脫靶量減小了35%，且能量消耗更少，PNG脫靶量較大。

4.3 目標正弦機動

目標做正弦機動，目標的縱向過載變化規律為

仿真結果如圖 6～ 8所示。

圖6中，FOSMG的彈道介于PNG與FTSMG之間，彈道最為平直，最接近零控攔截的狀態。結合圖7～8，FOSMG與FTSMG都能在制導初期做出較大機動來調整彈道，使攔截彈達到零控攔截的狀態。隨著目標機動，視線角速率發生變化，FTSMG一直施加較大過載，調整攔截彈跟隨目標機動，對目標機動進行補償，使視線角速率一直穩定在零附近。FOSMG在制導初期過載略大于FTSMG，對視線角速率的調整更迅速，收斂速度更快，具有更高的制導精度，最大過載小于FTSMG。

表3考察了目標正弦機動時不同制導律的攔截能力。PNG脫靶量很大，無法對目標進行直接碰撞攔截。FOSMG能量消耗略小于FTSMG。相對于FTSMG，FOSMG具有更小的脫靶量。

5 結? 論

針對高速機動目標的攔截模式和制導需求，本文提出了一種基于分數階滑模控制的制導律設計方法。仿真結果表明，FOSMG能夠實現對目標的精確攔截，且能量消耗更小，在迎頭攔截高速機動目標時具有良好的攔截性能。

FOSMG不含切換項，沒有抖震，過載整體變化平穩，最大過載較小，有利于彈上實現。分數階的計算需要對歷史數據重復計算，解算時間長，可以設計并行算法，縮短解算時間，隨著彈上計算機的計算能力增強，工程應用是可行的。

雖然能通過無限狀態方法和Lyapunov穩定性理論證明視線角速率沿著分數階滑模面收斂，但收斂時間和收斂方式由分數階的階次等多個參數決定，各個參數間的關系以及如何選取具有最優攔截性能的參數還需進一步探究。

參考文獻：

[1] 王榮剛，唐碩. 攔截高速運動目標廣義相對偏置比例制導律[J]. 西北工業大學學報，2019，37（4）： 682-690.

Wang Ronggang，Tang Shuo. Intercepting Higher-Speed Targets Using Generalized Relative Biased Proportional Navigation[J]. Journal of Northwestern Polytechnical University，2019，37（4）： 682-690.（in Chinese）

[2] 周覲，雷虎民. 真比例導引反高速目標攔截能力分析[J]. 系統工程與電子技術，2018，40（10）： 2296-2304.

Zhou Jin，Lei Humin. Interception Capability Analysis of the True Proportional Navigation Guidance Law Against Hypersonic Targets[J]. Systems Engineering and Electronics，2018，40（10）： 2296-2304.（in Chinese）

[3] 李轅，趙繼廣，閆梁，等. 攔截高速機動目標三維聯合比例制導律設計[J]. 北京航空航天大學學報，2015，41（5）： 825-834.

Li Yuan，Zhao Jiguang，Yan Liang，et al. United-Proportional-Navigation Law for Interception of High-Speed Maneuvering Targets[J]. Journal of Beijing University of Aeronautics and Astronautics，2015，41（5）： 825-834.（in Chinese）

[4] 常曉飛，孫博，閆杰，等. 針對高速機動目標的三維非線性微分對策制導律[J]. 彈道學報，2018，30（3）： 1-6.

Chang Xiaofei，Sun Bo，Yan Jie，et al. Three-Dimensional Nonlinear Differential Game-Based Guidance Law Against High-Speed Maneuvering Target[J]. Journal of Ballistics，2018，30（3）： 1-6.（in Chinese）

[5] 張旭，雷虎民，李炯，等. 基于改進視線坐標系的三維L2-增益制導律研究[J]. 固體火箭技術，2014，37（4）： 463-468.

Zhang Xu，Lei Humin，Li Jiong，et al. Three-Dimensional Gui-dance Law with L2-Gain Based on Modified Line-of-Sight Coordinate System[J]. Journal of Solid Rocket Technology，2014，37（4）： 463-468.（in Chinese）

[6] 段美君，周荻，程大林. 基于有限時間理論的臨近空間攔截器末制導律PWPF調節器研究[J]. 航空學報，2018，39（1）： 273-282.

Duan Meijun，Zhou Di，Cheng Dalin. Development of Terminal Guidance Law and PWPF Modulator for Near Space Interceptor Based on Finite Time Theory[J]. Acta Aeronautica et Astronautica Sinica，2018，39（1）： 273-282.（in Chinese）

[7] Pop C I，Ionescu C，De Keyser R，et al. Robustness Evaluation of Fractional Order Control for Varying Time Delay Processes[J]. Signal，Image and Video Processing，2012，6（3）： 453-461.

[8] Caponetto R，Dongola G，Fortuna L，et al. Fractional Order Systems[M]. Singapore： World Scientific，2010.

[9] Hu X R，Song Q，Ge M，et al. Fractional-Order Adaptive Fault-Tolerant Control for a Class of General Nonlinear Systems[J]. Nonlinear Dynamics，2020，101（1）： 379-392.

[10] Azar A T，Taher A，Vaidyanathan S，et al. Fractional Order Control and Synchronization of Chaotic Systems[M]. Springer International Publishing，2017.

[11] Sun G H，Zhu Z H. Fractional-Order Tension Control Law for Deployment of Space Tether System[J]. Journal of Guidance，Control，and Dynamics，2014，37（6）： 2057-2062.

[12] Almeida R，Torres D F M. A Discrete Method to Solve Fractional Optimal Control Problems[J]. Nonlinear Dynamics，2015，80（4）： 1811-1816.

[13] Vishal K，Agrawal S K，Das S. Hyperchaos Control and Adaptive Synchronization with Uncertain Parameter for Fractional-Order Mathieu-van der Pol Systems[J]. Pramana，2016，86（1）： 59-75.

[14] 史金光，王中原，常思江，等. 制導彈箭分數階控制系統[J]. 南京理工大學學報：自然科學版，2011，35（1）： 52-56.

Shi Jinguang，Wang Zhongyuan，Chang Sijiang，et al. Fractional-Order Control Systems for Guided Projectiles[J]. Journal of Nanjing University of Science and Technology： Natural Science，2011，35（1）： 52-56.（in Chinese）

[15] 王飛，雷虎民. 基于分數階微積分PDλ比例導引制導規律[J]. 控制理論與應用，2010，27（1）： 126-130.

Wang Fei，Lei Humin. PDλ Guidance Law Based on Fractional Calculus[J]. Control Theory & Applications，2010，27（1）： 126-130.（in Chinese）

[16] 葉繼坤，韋道知，李炯，等. 基于分數階微積分理論的新型三維末制導律[J]. 固體火箭技術，2016，39（3）： 428-435.

Ye Jikun，Wei Daozhi，Li Jiong，et al. Novel 3D Terminal Gui-dance Law Based on the Theory of Fractional Order Calculus[J]. Journal of Solid Rocket Technology，2016，39（3）： 428-435.（in Chinese）

[17] Yu S H，Yu X H，Man Z H. Robust Global Terminal Sliding Mode Control of SISO Nonlinear Uncertain Systems[C]∥Proceedings of the 39th IEEE Conference on Decision and Control，2000： 2198-2203.

[18] Trigeassou J C，Maamri N，Sabatier J，et al. A Lyapunov Approach to the Stability of Fractional Differential Equations[J]. Signal Processing，2011，91（3）： 437-445.

[19] Srivastava R，Ghose D，Sarkar A，et al. Three Dimensional Nonlinear Inverse Dynamics Guidance Law for Parallel Navigation[C]∥AIAA Guidance，Navigation，and Control Conference and Exhi-bit，2004.

[20] 趙杰，王君，張大元，等. 反臨近空間高超聲速飛行器中末交接視角研究[J]. 飛行力學，2015，33（3）： 253-256.

Zhao Jie，Wang Jun，Zhang Dayuan，et al. Visual Angle Research for Midcourse and Terminal Guidance Hand-over of Near Space Hypersonic Vehicles[J]. Flight Dynamics，2015，33（3）： 253-256.（in Chinese）

Fractional Sliding Mode Guidance Law for

High Speed Maneuvering Targets

Tang Xiao，Ye Jikun*

（Air and Missile Defense College，Air Force Engineering University，Xian 710051，China）

Abstract： Aiming at the interception problem of high speed maneuvering targets，a guidance law design scheme based on fractional-order sliding mode control theory is proposed. First，with the idea of fast terminal sliding mode plane，fractional order terms of line-of-sight angle rate are introduced into the fast terminal sliding mode dynamic plane to construct a fractional order dynamic sliding mode hyperplane. Then，combined with fractional calculus theory，the fractional sliding mode guidance law is derived on the basis of fractional dynamic sliding mode hyperplane，and the stability of fractional sliding mode guidance law is proved by using infinite state method and Lyapunov stability theory. The simulation results show that the guidance law can make the line-of-sight? angle rate converge within 2 s，the average overload is small，the guidance accuracy is higher，and the terminal miss distance is within 0.5 m.

Key words： guidance law;fractional sliding mode;infinite state method;finite time convergence;high speed maneuvering target;interception

收稿日期：2020-08-28

基金項目：國家自然科學基金項目（61703421）

作者簡介：唐驍（1995-），男，四川安岳人，碩士研究生，研究方向是飛行器制導控制。

通訊作者：葉繼坤（1984-），男，山東聊城人，副教授，研究方向是飛行器制導控制。