無后坐炮渦輪尾翼彈膛內流場數值模擬分析

郁家耀，蔣瀟蓉，周君濤，何 永，薛 濱

(南京理工大學 機械工程學院， 南京 210094)

1 引言

無后坐炮是一種特殊火炮。在射擊過程中利用火藥燃氣經過炮尾噴管后噴的反作用來消除炮身的后坐，使火炮達到平衡。付麗華等[1]建立了無后坐炮一維兩相流內彈道模型，獲得了膛內不同時刻的壓力、速度分布。龐春橋等[2]通過實驗方法對無后坐炮發射時的沖擊波超壓、熱流強度以及燃氣射流噴射時的氣流沖量進行了綜合測試。蔣瀟蓉等[3]基于ADAMS建立了無后坐炮與三腳炮架的多剛體模型，對火炮的射擊穩定性進行了分析。

滑膛式無后坐炮在發射增程破甲彈這種速度較高的彈丸時,常使用一種渦輪尾翼彈。渦輪尾翼彈出炮口后利用彈丸旋轉產生離心力來張開尾翼，轉速由無后坐炮后噴氣流推動尾桿上的渦輪提供。張陳曦等[4]假設后噴氣流為一維不可壓縮流動，結合庫塔-儒可夫斯基公式和半封閉彈道原理對彈丸轉速進行了推導。

本文以一種渦輪尾翼彈無后坐炮為研究對象，利用計算流體力學方法耦合內彈道模型，對這種無后坐炮發射過程中的膛內流場進行研究。

2 物理模型

本文研究的82滑膛式無后坐炮的結構示意如圖1所示。

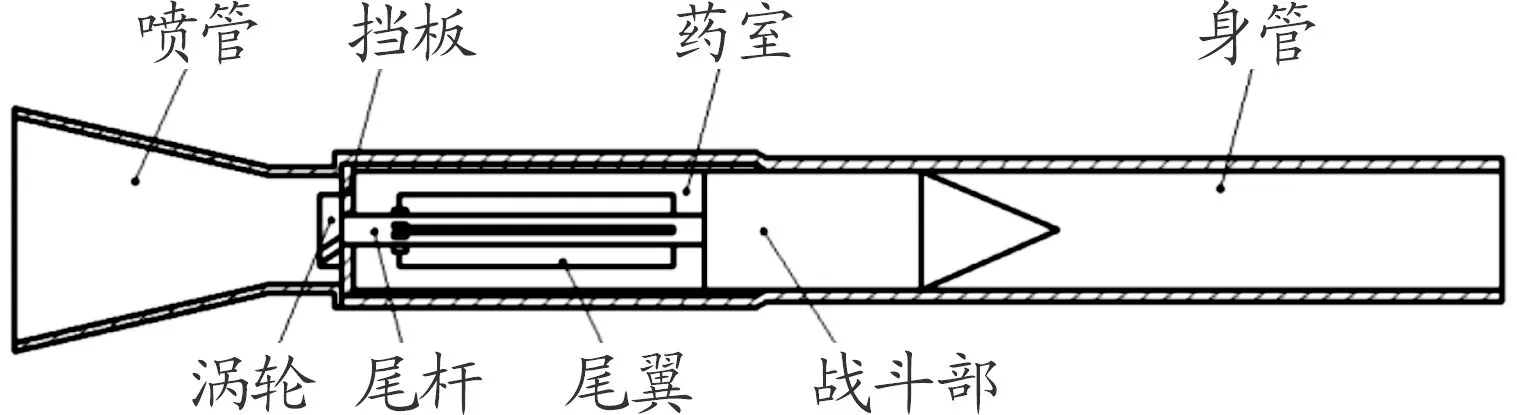
圖1 結構示意圖

這種存在渦輪結構的彈體在發射時，火藥在藥室內定容燃燒，藥室內的火藥氣體一部分推動彈丸向前運動，另一部分通過渦輪流入炮膛并經過噴管噴出，從而構成了火藥氣體的二次膨脹過程。

3 數學方程

傳統的經典內彈道模型，一般假設膛內火藥氣體為一維流動，而計算流體力學方法可以建立膛內火藥氣體流動的二維甚至三維模型。由于這種彈體存在渦輪的結構，為了分析這種結構所引起的彈道特點，利用計算流體力學軟件Fluent，耦合經典內彈道模型對膛內二維流場進行分析。

3.1 經典內彈道模型[5-6]

建立適用于渦輪尾翼彈的經典內彈道模型如下：

幾何燃燒定律方程為：

ψ=χZ-χλZ2

(1)

式(1)中：ψ為火藥已燃百分比；Z為火藥已燃相對厚度；λ與χ為火藥形狀特征量。

燃速方程為：

(2)

式(2)中：p為藥室內壓力；u1為燃速系數；e1為火藥弧厚。

藥室內壓力為：

(3)

3.2 彈丸運動方程

以炮口方向為正方向，則靠近藥室的一面為渦輪前壁，靠近噴管的一面為渦輪后壁。由于渦輪前后的壓力不同，渦輪尾翼彈的彈丸運動速度受彈底壓力與渦輪后壁壓力的影響而不斷變化。彈丸運動方程為:

(4)

式(4)中：S1為彈底面積；S2為渦輪后壁面積；p2為渦輪后壁所受壓力。

3.3 計算流體力學方程[7]

基于膛內火藥氣體流動具有軸對稱性質，建立火藥氣體流動的二維軸對稱雷諾平均Navier-Stokes方程為：

(5)

式(5)中：ρ為氣體密度；e為單位氣體比內能；ur和uz分別為氣體軸向與徑向速度。

標準k-ε模型是工業上應用最廣泛的湍流模型，其求解2個變量，湍流能量k和湍流能量耗散率ε，利用渦粘方法模擬雷諾應力，具有良好的收斂速率和相對較低的內存需求，但對于高時均應變流動會出現負的正應力這種非物理的結果，為避免這種情況，本文采用其改進型Realizablek-ε模型。

湍流能量輸運方程可表示為：

τtijSij-ρε+φk

(6)

湍流能量耗散輸運方程表示為：

(7)

式(7)中：右端項分別表示生成項、耗散項和壁面項；常數值為：Cε1=1.45，Cε2=1.92,σk=1.3。

4 耦合內彈道方程組的計算模型

4.1 邊界條件及網格劃分

忽略渦輪葉片旋轉對氣流的影響，并通過等效體積法將渦輪及尾部諸元件等效為圓柱體，建立二維軸對稱流體計算模型如圖2所示。

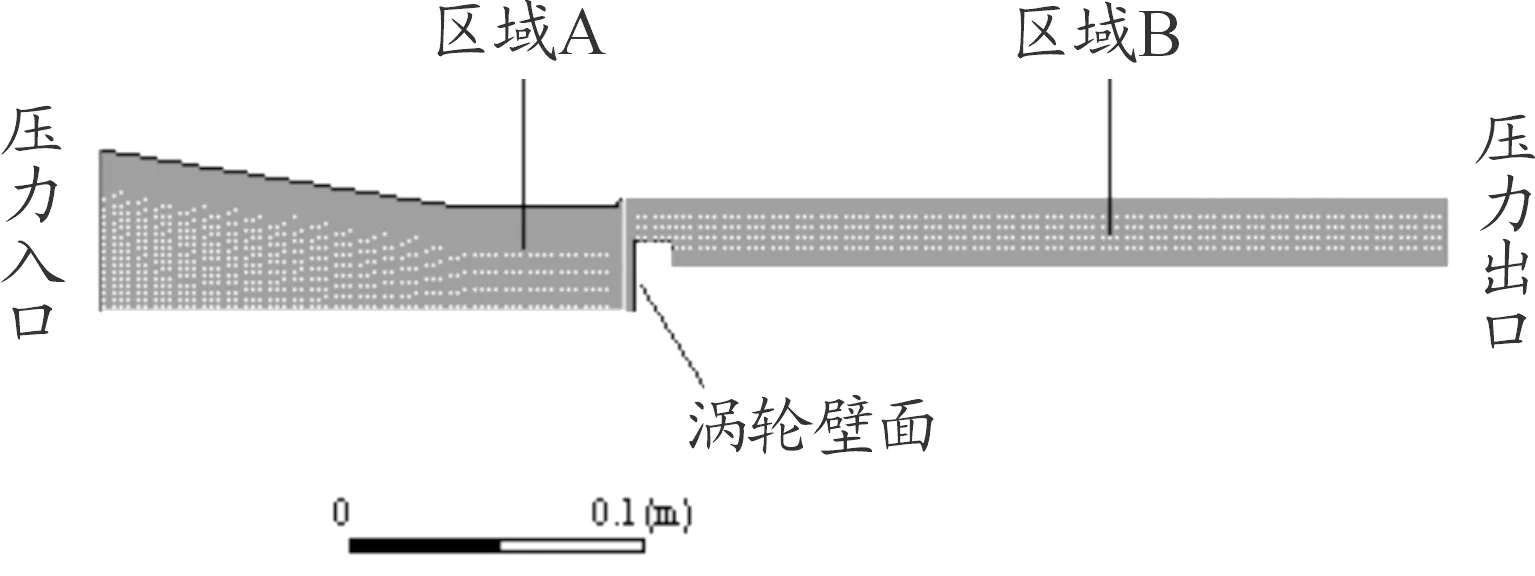
圖2 膛內流場計算模型示意圖

計算域總長度為501.4 mm，以噴管入口為交界面劃分為2個區域，均采用四邊形結構網格劃分，最大網格尺寸1.5 mm，最小網格尺寸0.05 mm，共12 267個網格。身管、渦輪、尾桿、噴管壁面均假設為絕熱無滑移壁面。藥室底部設為壓力入口邊界，噴管出口設為壓力出口邊界，出口壓力值由超音速氣流壓力外推得到。

4.2 耦合內彈道方程組

由文獻[5]可知，渦輪尾翼彈的經典內彈道方程一般通過假定渦輪后方空間初始狀態為真空，全由渦輪排氣流出的氣體填充，結合真空膨脹理論確定渦輪后壁壓力并推導彈丸運動速度，這與真實情況誤差較大。基于膛內氣流運動的復雜性，本文采用Fluent與內彈道方程組雙向耦合的方法，獲得更符合真實情況的膛內流場，每個時間步之間與內彈道子程序進行數據交換。每一個時間步迭代開始前求解內彈道程序，將計算得到彈丸運動速度與壓力數據等通過UDF傳遞至Fluent，迭代收斂后再通過UDF將氣體流量與渦輪后壁壓力代入內彈道方程組，再將計算得到的內彈道參數通過UDF傳遞至Fluent，……，依次循環直至彈丸飛出炮口[8-9]。耦合內彈道方程組的計算流程如圖3所示。

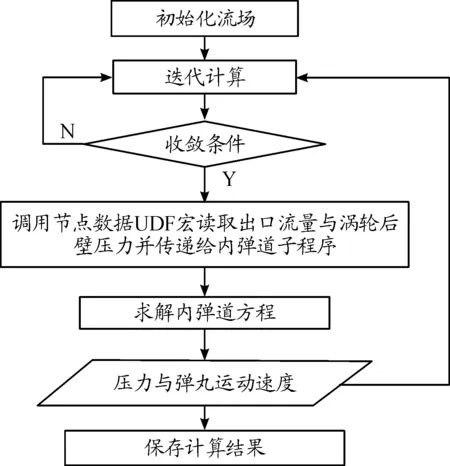
圖3 耦合內彈道方程組的計算流程框圖

根據式(3)計算得到壓力入口邊界的壓力值。式(3)中η的值通過F_FLUX宏函數讀取渦輪排氣斷面網格節點的質量流量得到，傳遞至內彈道程序求解得到藥室壓力p，最后通過DEFINE_PROFILE宏函數定義為入口壓力。

動網格運動速度由式(4)計算得到，利用F_P()宏獲得渦輪后壁網格面壓力，代入內彈道方程組得到彈丸運動速度，最后通過CG_MOTION宏函數賦值給區域B。

動網格方法采用區域整體運動結合動態層變的方法。區域A為網格變形區，區域B為剛性運動區。區域B以彈丸運動速度向右運動，并拉伸分裂交界面處的網格。

4.3 初始化

假設該無后坐炮藥室壓力達到5 MPa時，噴管打開并且彈丸起動。

流場計算由噴管打開開始，分別初始化藥室內壓力為 5 MPa，噴管內壓力為標準大氣壓。時間步間隔0.001 ms。

5 流場仿真結果與分析

仿真結果顯示，在彈丸起動約4.8 ms后，彈底到達炮口，炮口初速約為209.58 m/s，實驗測得炮口初速為210.8 m/s，與實驗值接近。

5.1 膛內壓力與速度分析

圖4、圖5分別描述了不同時刻膛內壓力與氣流速度分布情況。無后坐炮射擊時，藥室內火藥燃燒，使得膛壓升高，高溫高壓氣體經過渦輪和噴管喉部時速度加快，最后在噴管擴張段迅速膨脹。開始階段，渦輪靠近噴管喉部，氣流速度較小，火藥氣體受到渦輪的阻擋作用較大，導致壓力在渦輪前壁面處達到最大。隨著藥室內火藥燃燒，渦輪前后壓力差不斷增大，前后區域壓力開始呈現明顯的不同。當火藥燃盡后，前后壓力差減小，但渦輪后壓力仍明顯小于藥室內壓力。

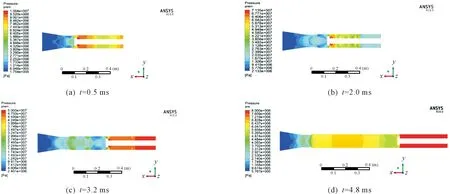
圖4 同時刻膛內壓力分布云圖

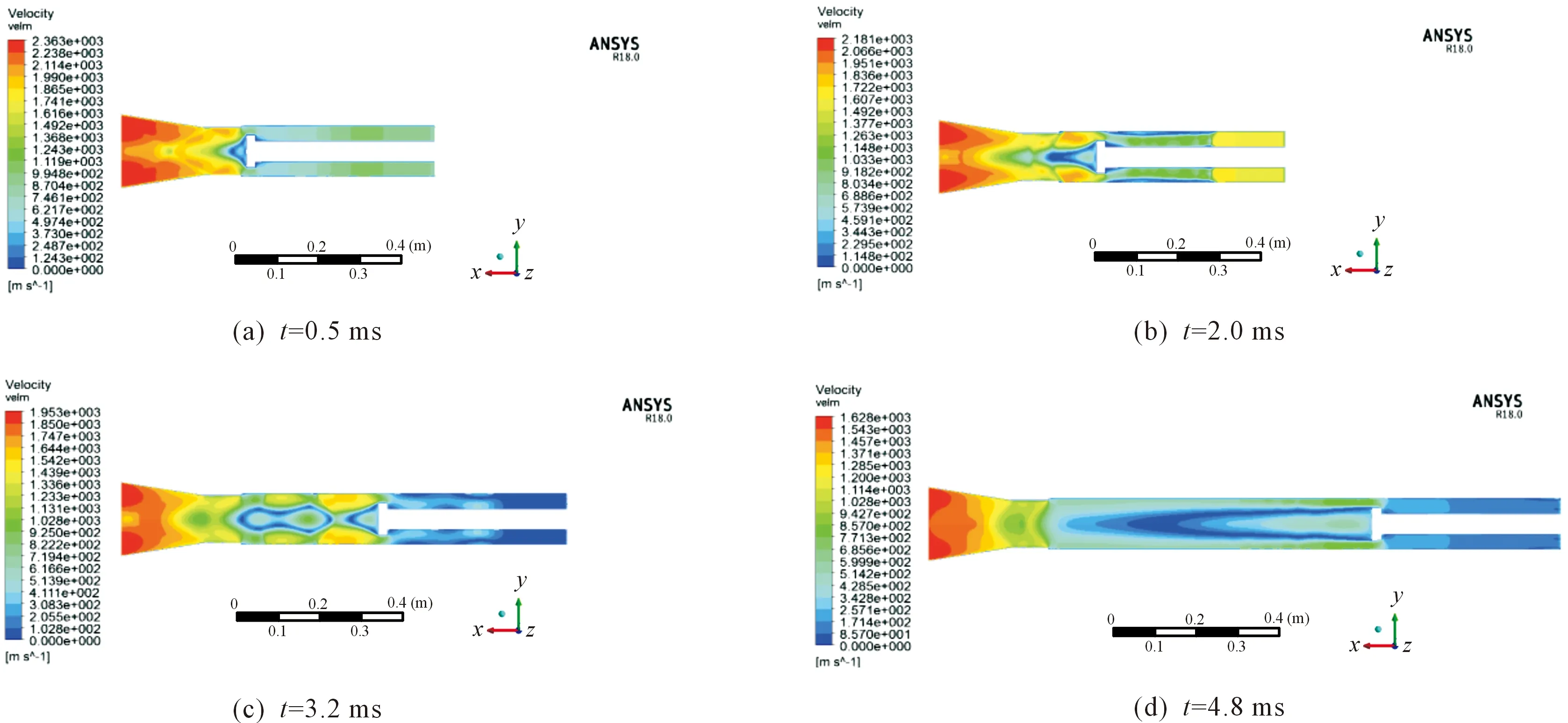
圖5 不同時刻膛內氣流速度分布云圖

在渦輪后壁面，由于渦輪快速向前運動與喉部入口的幾何形狀對火藥氣體的阻擋作用，渦輪后氣體在這個區域存在回流現象，回流區域內出現旋轉的渦流。且渦輪的運動還對后方氣體產生類似“抽真空”的效果，使得渦輪后壁壓力相對于其他區域較低，這也與實際情況比較吻合。

5.2 不平衡力與不平衡沖量

無后坐炮動不平衡是無后坐炮發射時“無后坐”實現系統平衡性能的重要指標。該滑膛式無后坐炮發射時，作用于炮身的不平衡力主要由氣流作用于噴管喉部入口端面的軸向力與作用于噴管擴張段的推力組成[10]。

根據流場仿真結果處理得到的不平衡力變化曲線如圖6所示。在整個膛內運動過程中，由于膛內氣流的非定常流動，同一瞬間噴管與噴管喉部入口端面所受氣流的軸向力不等，這種影響導致了整個炮身受到不平衡力的作用，整體上炮身所受不平衡力呈現出先增大后減小并趨于平緩的震蕩過程，最大約為8 kN。

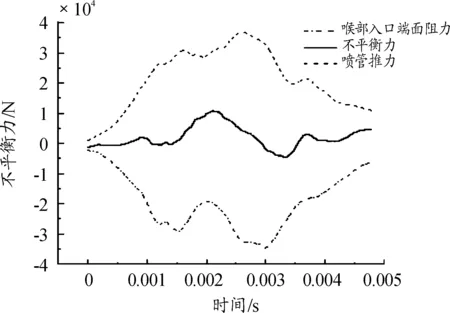
圖6 不平衡力變化曲線

彈丸起動初期，膛內壓力增加，氣流對喉部入口端面的推力也不斷增大，同時噴管擴張段受到的氣流推力也不斷增大。隨著彈丸向前運動，渦輪遠離喉部，喉部入口端面的氣流在一段時間內受到渦輪后方渦流的影響，導致作用在端面上的壓力驟降，不平衡力也因此達到最大。在經過一段時間后，隨著渦輪繼續向前運動，噴管推力與端面阻力重新增大，直到火藥燃燒結束，膛內壓力降低，噴管推力與端面阻力也隨之降低，不平衡力曲線趨于平緩。

根據不平衡力計算整個膛內運動時期作用于炮身的不平衡沖量為：

實際應用中，對無后坐炮不平衡沖量的允許值大約為10 N·S，仿真計算得到的不平衡沖量的值與實際情況接近，可為結構的進一步優化提供理論依據。

6 結論

1) 計算流體力學與內彈道方程組的耦合模型，適用于渦輪尾翼彈無后坐炮的膛內流場計算，通過該方法可以觀察到詳細的膛內流場分布。

2) 渦輪結構對膛內火藥氣體有明顯的阻擋作用，渦輪后氣流處于渦流狀態，渦輪后區域壓力始終低于渦輪前區域壓力。

3) 炮身所受不平衡力受到渦輪的影響，渦輪后方渦流導致短時間內噴管入口處火藥燃氣壓力降低，不平衡力增大，該結論可對渦輪與身管的設計與優化提供參考。