平行束CT系統參數標定的多目標優化模型

曠 敏，牟廉明，鄭云升，葉 薇，邱利瓊

（1.重慶理工大學 理學院，重慶 400054；2.內江師范學院 數學與信息科學院，四川 內江 641100；3.西華大學 理學院，成都 610039；4.顧縣中學，四川 廣安 638000）

1 背景

CT技術可在不破壞物體的前提下，通過斷層掃描清晰直觀地觀測到物體的結構，其掃描部分由X射線、介質樣品和一定數量的探測器組成，是一種利用X光對物體進行掃描來檢測目標斷層的投影技術［1－2］。Radon提出投影重建原理后，Hounsfield于1972年在英國放射學會上首次公布第1臺CT系統掃描裝置，從此CT技術得到迅猛發展［3－4］。而CT系統在安裝時往往存在誤差，導致成像質量差，因此提高CT系統幾何參數的準確性和精確度的研究顯得尤為重要。

目前，對CT系統幾何參數標定方法的研究比較活躍。1999年，Gullberg等［5］利用質點在探測器上運動形成的投影標定出橢圓形參數，從而得到CT系統的幾何參數。2000年，Noo等［6］利用最小二乘法擬合出標定模體的橢圓形投影軌跡，并與系統的幾何參數組合成關系式，從而確定CT系統的幾何參數。2006年，Liu等［7］比較了心圖法、對角插值法、曲線擬合和幾何法4種方法來測定CT系統旋轉中心（COR）的精確性。同年，孫怡等［8］選擇基于4個點狀目標的金屬板作為定標模型，利用標準模型的某一固定角度下的投影數據標定幾何參數。2009年，李保磊等［9］提出利用正弦圖數據的冗余性采用總和均分的方式來確定COR的位置。2013年，孟凡勇等［10］利用中心投影具有π分割數據一致性的特點，提出利用原始數據精確確定COR的方法。2018年，龍建輝等［11］基于圖像輪廓曲線的提取，通過建立數學模型來標定CT系統參數。2019年，夏彬珂等［12］和李江珊等［13］采用最小二乘法擬合優化函數，并利用遺傳算法求幾何參數的值。以上方法側重提高COR的精確性，十分依靠算法，并在特定條件下才可以求出精確解，條件改變后，方法就不一定適用。據此，為提高X射線平行入射的二維CT系統幾何參數的精確性，并適用于不同模板，從多目標規劃角度，提出一種多目標優化模型。當條件增加或減少時，模型精確度高、適用性強且穩定。

2 不同模板的幾何參數標定優化問題及建模

對于典型的CT系統，平行入射的X射線垂直于探測器平面，將每個探測器單元看成一個接收點，且等距排列。X射線的發射器和探測器相對位置固定不變，整個發射－接收系統繞某固定的旋轉中心逆時針旋轉180次。對每個X射線方向，在具有512個等距單元的探測器上測量經位置固定不動的二維待檢測介質吸收衰減后的射線能量，并經過增益等處理后得到180組接收信息。

2.1 第1類模板：正方形托盤上放置均勻介質圓

在100 mm×100 mm正方形托盤上放置1個均勻固體介質（半徑為25 mm圓）組成的模板，模板的幾何信息如圖1所示。求CT系統的幾何參數，即X射線入射方向（IDX）、CT系統旋轉中心（COR）和探測器單元間距（DUS）。

圖1 第1類模板示意圖

1）確定任意1條X射線方程

將模板的正方形托盤中心與圓中心重合，建立平面直角坐標系。為進一步確定COR與512條X射線之間的幾何關系，任取1個點作為旋轉中心點o′（x0，y0），任取X射線的1個初始方向為θ。由于探測器單元是等距排列的，當平行光入射時，旋轉中心點到每條射線的距離都可以表示，如圖2。假設X射線從不同方向入射的DUS不同，用Dj來表示，則任意1條X射線到旋轉中心o′的距離…，180。

圖2 X射線任意1個入射角度示意圖

根據圖3，作經過點o′（x0，y0）的射線l0，設射線l0與y軸交點的縱坐標為a0，則射線l0的斜截式為y0＝tanθjx0＋a0，即a0＝y0－tanθjx0。任意1條射線在線段l0的下方或上方，可以得到圖3所示的幾何關系，則構成一個直角三角形△A0A′iAi，可以求得ai。設點Ai到A0的距離為a′i，則a′i＝因此任意1條X射線與y軸的相交點Ai的縱坐標為ai＝a0－a′i。綜上，可以得到任意1條X射線的直線方程是y＝tanθjx＋ai。即：

圖3 任意1條射線與l0兩種位置關系示意圖

2）建立超定方程組

根據定義，圓的標準方程為x2＋y2＝252，單位為mm。聯立射線與圓的方程組：

3）建立第1類模板的CT系統參數標定優化模型

需要求解該模板下CT系統的幾何參數，即IDX、COR和DUS。于是確定決策變量為IDX范圍為θj、COR的坐標位置為o′（x0，y0）和DUS為Dj。

512條X射線穿過模板后，會在探測器接收器上顯示接收信號，因此DUS需要滿足一定的范圍，從而使得X射線從不同方向入射時DUS最小，因此確定目標函數為180組方向下DUS的平均方差和最小，即。為減少旋轉中心的偏差，當旋轉中心越接近坐標原點時，512根X射線在180組方向下更容易檢測。于是選擇目標函數為旋轉中心點o′到坐標原點o的距離最小，即

有3類條件對其約束。

約束1：X射線與圓不相交。當X射線與物體相交時，X射線強度會衰減，因此探測器上接收的信號弱。滿足Δ≤0條件，即：

約束2：當不同入射方向的X射線發生強度衰減時，確定探測器單元間距范圍。已知射入的X射線有512組，X射線入射角度有180組，因此不同的入射角度會影響DUS。為精確確定DUS范圍，根據幾何關系，用圖4中3種角度入射計算得DUS范圍為：

圖4 X射線3種入射角度示意圖

約束3：自身范圍限制。在平面上，平行束IDX范圍為一周，即0≤θj≤2π。由于圓在正方形托盤中，則COR一定在模板上，即

綜上，得到第1類模板的CT系統多目標參數優化模型，i＝1，2，…，512，j＝1，2，…，180。

2.2 第2類模板：正方形托盤中放置非均勻介質橢圓和圓

在100 mm×100 mm正方形托盤上放置由2個非均勻固體介質（長半軸為15 mm、短半軸為40 mm的橢圓和半徑為4 mm的圓）組成的模板，模板的幾何信息如圖5所示。其他條件相同，求CT系統的幾何參數。

圖5 第2類模板示意圖

1）確定任意1條X射線方程

在本模板中固體介質為非均勻的，且從1個上升為2個，即增加了橢圓。為確定模板下的多目標優化模型，利用相同的建模思路。X射線不論射入橢圓還是圓都會發生衰減，根據圖7的幾何關系確定任意1條X射線方程過程相同，則可以確定任意1條X射線方程為y＝tanθjx＋bi，其中2，…，512，j＝1，2，…，180。

2）建立超定方程組

圖6 X射線任意1個入射角度示意圖

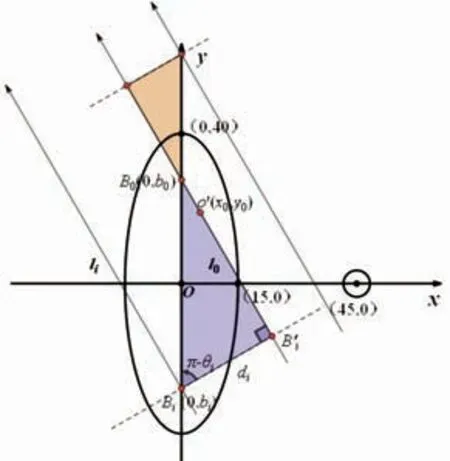
圖7 射線和l0兩種位置關系示意圖

同樣，利用弦長公式組成超定方程組，則橢圓和圓的弦長分別為：

3）建立第2類模板的CT系統參數標定優化模型

其中：k＝2，3，i＝1，2，…，512，j＝1，2，…，180。

3 適用于不同模板下平行束CT系統參數標定的多目標優化模型

為提高CT系統幾何參數的準確性和精確度，并保證在樣品數量改變的情況下精確度相對較高，根據式（4）和式（8）兩個模型，在構成模板樣品數量不同、形狀不同、介質不同時，提出平行束CT系統參數標定的多目標優化模型。則利用射線與模板上樣品之間的幾何關系，以COR的坐標（x0，y0）、探測器單元間距（DUS）和X射線的入射方向（IDX）為決策變量，以X射線從180個方向入射時DUS方差和的平均值最小和旋轉中心點o′到坐標原點的距離最小為目標函數，以X射線與介質樣品不相交、3種方向入射時（即水平、豎直、東北45°方向）確定IDX范圍和自身限制為約束條件，建立適用于不同模板的平行束CT系統參數標定的多目標優化模型。

其中：用Dj表示DUS，n表示整個發射－接收系統繞旋轉中心的次數，j＝1，2，…，n。探測器的個數為m，i＝1，2，…，m。利用判別式Δrij表示X射線是否射入樣品中，X射線被截斷的弦長用lrij表示，r為X射線射入不同樣品的數量，r＝1，2，3，…。探測器間距與正方形托盤和樣品大小有關，因此最大間距和最小間距分別用c和d表示。COR在正方形托盤內，因此橫縱坐標確定。用θj表示IDX，考慮發射－接收系統按逆時針旋轉是在1周內，即θj∈［0，2π］。

4 定量分析

參考文獻［21］的部分數據，擬合并多次迭代求解第2類模板的幾何參數，得到結果：CT系統的旋轉中心（COR）為（－9.213 4，6.035 1），探測器單元間距（DUS）為0.276 2 mm，X射線入射初始方向（IDX）為120.210 0°，每次逆時針旋轉約0.997 1°，并得到180組方向。

為驗證模型的精度，以第2類模板為例，將幾何參數結果和9個樣本［12－20］的初始IDX、COR和DUS與樣本1的數據［22］進行誤差分析。分別得到10個樣本初始IDX、COR和DUS的誤差數據，具體見表1～3。

表1 IDX誤差分析

表2 COR誤差分析

表3 DUS誤差分析

由表1～3可知：第2類模板的初始IDX為0.563 7°＜0.617 7°；COR的誤差距離0.248 5 mm＜0.640 1 mm；DUS的誤差為0.000 6 mm＜0.000 8mm。3部分都低于平均值，且COR的誤差距離僅次于樣本3、4，而本文中DUS的誤差僅為0.000 6 mm，誤差非常小。從整體上看，利用提出的優化模型求解出的CT系統的參數比現有大部分結果更精確，因此所提出的優化模型可行度高，精確度也較高。

5 模型應用

為考察模型的實際使用情況，檢驗模型的穩定性，選擇第2類模板進行應用驗證。根據計算出的幾何參數和文獻數據［21］重建圖像，并與精度較高的樣本3的圖像進行對比，檢查成像的質量，進而說明模型的穩定性。

由于模板上的樣品對X射線有吸收和散射作用，導致X射線發生衰減。將模板上介質樣品的各單位近似均勻處理，得到X射線衰減系數公式根據文獻［23］，基于Radon變換和反變換原理，利用Matlab內置圖像重構函數iradon，采用濾波反投影算法重建圖像。此時，圖像需要校正，采用簡單的平移、旋轉，平移前后坐標用（x，y）與（x′，y′）表示，在水平和豎直方向的偏移量分別用d x，d y表示，旋轉角度用α表示。

由圖8、9可知，校正后的圖像不僅消除了偽影，而且圖像的邊緣更光滑，輪廓更清晰。將本文的校正圖像與樣本3的校正圖像對比，雖然圖像重建的算法不同、模型不同，但兩者差別甚微。由此可見，所提出的多目標優化模型重建的圖像能達到其他方法重建的效果。換言之，說明本文中模型在保證成像質量的同時精度高，表明模型的穩定性強。

圖8 第1個圖校正前、本文方法校正后和 樣本3校正后的圖像

圖9 第2個圖校正前、本文方法校正后和 樣本3校正后的圖像

6 結論

為提高平行束CT系統幾何參數的精確性，從多目標規劃角度，提出一種平行束CT系統參數標定的多目標優化模型。該模型適用于不同數量、不同形狀、不同介質構成的模板。利用超定方程組方程多、求解值少且便于迭代優化的特點和幾何關系確定相應模板的多目標優化模型。通過分析發現，在不同數量、不同形狀、不同介質構成模板的條件下，兩類模板的模型結構類似，因此總結提出了一種平行束CT系統參數標定的多目標優化模型。通過對第2類模板的計算，并將9組樣本分別與樣本1數據進行定量分析發現，本文結果優于大部分樣本，精度較高。另外，將第2類模板的幾何參數結合相關數據重構圖像，發現相較于樣本3所重構的圖像差別不大。因此，本文中所提出的模型不但適用于該類問題，還能保證精度較高、穩定性較強。

由于未對圖像重建算法做深入研究，在多目標規劃領域，第2類模板的計算結果是全局最優解，而實際問題中可能不存在這樣的解。因此，需要進一步從多目標規劃問題出發求有效解，確保最優解在實際中一定存在。