求解柔性車間調度問題的雙層編碼離散布谷鳥算法?

羅浩嘉潘大志，2

（1.西華師范大學數學與信息學院 南充637009）（2.西華師范大學計算方法與應用研究所 南充637009）

1 引言

車間調度是現代企業制造的基礎，優化調度方案是先進企業亟待解決的關鍵問題，作業車間調度問題是典型的NP-hard問題，也是組合優化問題領域的研究熱點問題，有很強的工程應用背景。Johnson［1］于1954年首次討論了作業車間調度問題（Job-shop Scheduling Problem，JSP），而隨著制造業領域的進步和發展，柔性作業車間調度問題（Flexi?ble Job-shop Scheduling Problem，FJSP）應運而生，它是對傳統調度問題的進一步拓展和延伸。FJSP的求解主要包括精確算法［2］、啟發式算法［3］和智能優化算法。近年來，針對求解FJSP的智能優化算法越來越多，如遺傳算法［4］、蟻群算法［5］、粒子群算法［6］、禁忌搜索算法［7］、模擬退火算法［8］等。牛琳等［9］結合柔性作業車間調度的特點，采用模擬退火算法融合遺傳算法對調度領域進行了研究。王芳［10］等設計了一種混合隨機概率與規則解碼方法，擴大了搜索空間，阻止算法早熟。Xiong等［11］采用了新的生成機制來產生初始種群，從而加快了算法的收斂速度，從而減少了算法的運行時間。

布谷鳥搜索算法（Cuckoo Search，CS）是由Yang等［12］提出的一種新型元啟發式算法，由于其結構簡單容易實現、控制參數少、能有效平衡全局最優和局部最優并且等優點，已被成功應用于多個領域。Ouaar等［13］基于標準布谷鳥算法的思想，將布谷鳥算法離散化，用于求解車間調度問題。Han等［14］針對混合流水車間調度問題設計了自適應布谷鳥算法，并加強了算法跳出極值的能力。羅函明等［15］采用基于改進解碼方法的離散布谷鳥算法求解混合流水車間調度問題，提高了解的質量。由于集成編碼的個體只能簡單表示問題的解，在后續更新操作上會過于復雜和繁瑣，本文采用多層編碼把個體編碼分為兩層，每一層所代表的含義不同，復雜問題的解也可以用一個完整的個體編碼表示，很大程度上提升了算法的可讀性。

2 柔性作業車間調度問題

柔性車間調度可描述為有n個工件在m臺機器上加工，每個工件有一道或者多道加工工序，每道工序可以有多種可選擇的加工機器，其中每道工序只能由一個機器加工一次且必須等上一道工序加工完成才能進行下一次加工。調度的目標是為每道工序分配最合適的機器以及確定每臺機器上每道工序的加工次序，以滿足特定的優化目標。已知各工件的各工序在機器上的加工時間，要求確定工件加工順序和對應的機器分配情況，使得最大完工時間最小［16］。

符號定義：

n表示工件數量；

m表示工序數量；

Mj表示第j道工序的可使用機器集合；

Pijk表示工件i的工序j在機器k上的加工時間；

Sijk表示工件i的工序j在機器k上的開始加工時刻；

Cijk表示工件i的工序j在機器k上的結束加工時刻；

Njk表示工序j在機器k上加工的工件數量；

Pjk表示在工序j的機器k上進行加工的第R個工件。

本文優化的目標是最小化最大完工時間，其數學模型如下：

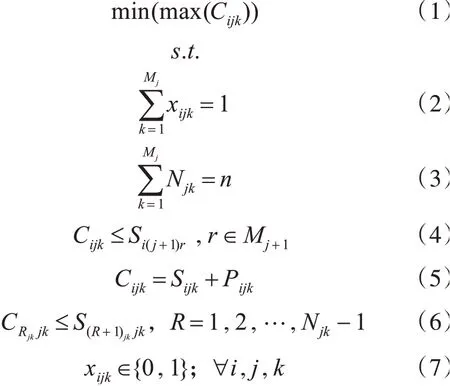
其中，i=1，2，…，n;j=1，2，…，m;k∈Mj，式（2）表示每個工件在每道工序只能被一臺機器加工；式（3）表示對每道工序，分配給工序內所有機器的工件數之和為n；式（4）表示對同一工件的加工，下一道工序必須在上一道工序結束后才能開始；式（5）表示對任何工件，其完成時間取決于其在某個機器上的加工時間和開始時間；式（6）表示每個機器在同一時間只能加工一個工序；式（7）為變量取值范圍。

3 多層編碼的離散布谷鳥算法

3.1 標準布谷鳥算法

2009年劍橋大學的Xin-SheYan和S.Deb通過模擬布谷鳥寄生育雛行為提出了布谷鳥算法（Cuckoo Search，CS），布谷鳥在繁殖期間并不自己筑巢，而是通過寄生的方式將自己的幼卵產在其他鳥類的鳥巢中讓其他鳥類孵化幼卵，為了提高繁殖率，布谷鳥在選擇宿主鳥窩時會選擇和自己卵形相似、卵的顏色、孵化周期一樣的鳥窩。即便如此仍然存在著被宿主發現寄生卵的可能性，幼卵一旦被宿主發現，宿主便會拋棄鳥巢重新筑巢。本文根據基本布谷鳥算法的核心思想，提出了改進的離散布谷鳥算法。

3.2 個體編碼

本文采用雙層整數編碼，第一層是基于工序的整數編碼，第二層是基于機器的整數編碼。在第一層編碼中，每個工件用一個整數表示，從左到右整數出現的順序就代表工件加工的先后順序；在第二層編碼中，整數代表每道工序對應選擇的機器序號。即個體的前半部分表示所有工件的加工順序，后半部分表示每道工序加工時選擇的機器序號。每一個完整的編碼序列就代表一個鳥巢信息，即待優化問題的一個可行解。具體編碼方式如圖1。

如圖1所示，該個體有四個工件，每個工件有兩道加工工序，可以在兩種機器上進行加工。其中，J21表示個體中工件2的第1道工序，T212表示工件2第1道工序在機器2上生產；J41表示工件4的第1道工序，T411表示工件4第1道工序在機器1上生產，以此類推。

圖1 離散布谷鳥算法多層編碼

3.3 離散levy飛行更新策略

在標準的CS算法中，levy飛行更新鳥巢位置是一種連續性的位置更新，因此本文需要設計一種適用于調度問題的離散levy飛行。由于levy飛行在搜索過程中伴隨著頻繁的短距離搜索以及少數長距離全局探索，短距離搜索用于在當前最優解周圍仔細搜尋提高局部搜索能力，而少數長距離跳躍式探索有利于擴大搜索范圍，使之更容易跳出局部最優。因此，本文通過2-opt操作代替levy飛行中的短距離搜索，用double-bridge（雙橋）操作代替levy飛行中長距離跳躍式搜索，通過2-opt與dou?ble-bridge結合代替levy飛行進行鳥巢位置更新操作。

1）2-opt move：又稱為“反序算子”，隨機選擇兩個不相鄰的點ci和cj，斷開ci和ci+1以及cj和cj-1之間的弧，并引入兩個新的弧，得到的新序列。如圖2，圖（a）為原始序列，圖（b）為2-opt操作后產生的新序列。若得到的新序列（b）優于原始序列（a），則更新序列；否則，繼續循環，直到得到更優的序列或者達到最大循環次數為止。

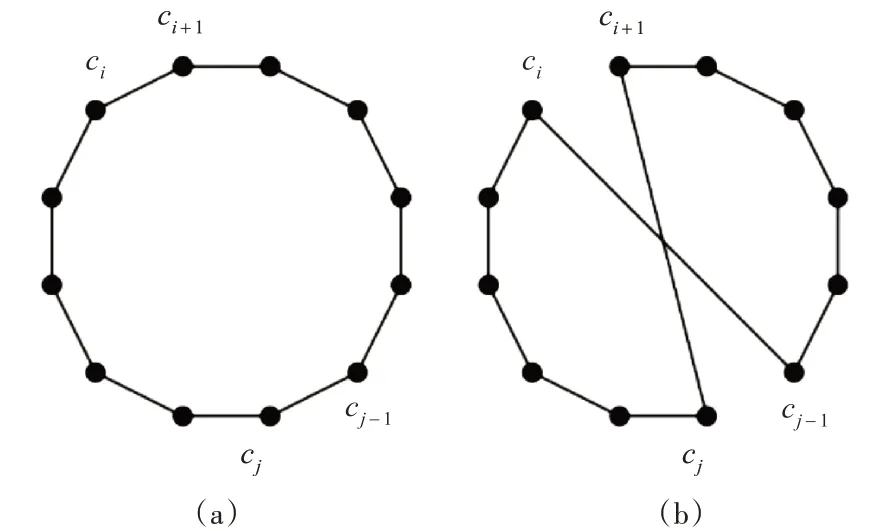
圖2 2-opt move

2）double-bridge move：隨機選擇四個不相鄰的點c0、ci、cj和ck，斷開c0和c1、ci和ci+1、cj和cj+1以及ck和ck+1之間的弧，并引入四個新的弧，得到新的序列。如圖3，圖（a）為原始序列，圖（b）為double-bridge操作后產生的新序列。若得到的新序列（b）優于原始序列（a），則更新序列；否則，保持原始序列。

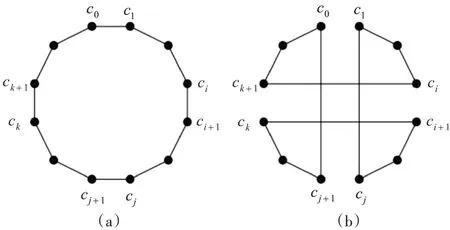
圖3 double-bridge move

3.4 隨機游走策略

本文采用基于擇優交換和擇優插入的巢寄生方式將標準CS算法中的隨機游走策略離散化。首先生成一個服從均勻分布的隨機數r，將其與被發現概率Pa進行比較，如果r>Pa則通過擇優交換或者擇優插入操作更新位置信息，否則，不對其進行位置更新操作。擇優插入操作和擇優交換操作的概率均為0.5。

1）擇優插入操作：隨機從工件加工序列中提取出一個工件號，將取出的工件號按照從左到右的順序，依次插入到剩下的序列中組成新序列，并將新序列與原序列進行比較，當新序列優于原序列時，退出擇優插入操作，否則，繼續進行擇優插入操作，直到無法進行插入操作為止，如圖4所示。

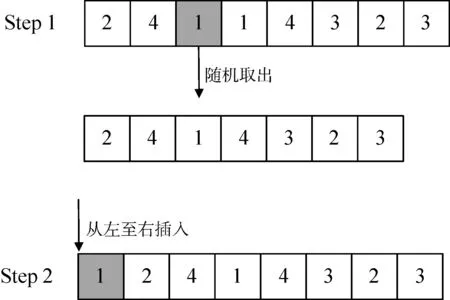
圖4 擇優插入操作

2）擇優交換操作：隨機從工件加工序列中選擇一個工件號，將所選工件號按照從左到右的順序，依次與剩下序列中的工件進行交換組成新序列，并將交換后的新序列與原序列進行比較，當新序列優于原序列時，退出擇優交換操作，否則，繼續交換操作，直到無法進行交換操作為止，如圖5所示。

圖5 擇優交換操作

3.5 算法描述

綜合以上步驟和結論，算法主要的流程如下。

Step 1初始化種群數量NIND，迭代次數MAX?GEN，鳥巢被發現概率Pa；

Step 2隨機產生初始序列，并計算每個序列對應的調度時間，找出當前最短調度時間并記為初始全局最短調度時間；

Step 3用2-opt操作與double-bridge操作結合使用代替levy飛行操作更新鳥巢位置。計算更新之后的調度時間，若比當前最短調度時間小，則更新全局最短調度時間；

Step 4生成一個服從均勻分布的隨機數r，將其與被發現概率Pa進行比較，若r>Pa則采用擇優交換或者擇優插入操作代替全局隨機游走策略對鳥巢位置進行更新。計算更新之后的調度時間，若比當前最短調度時間小，則更新全局最短調度時間；

Step 5檢查算法是否達到最大迭代次數，若達到最大迭代次數，停止算法迭代，輸出全局最短調度時間，若未達到則重復Step3、Step4。

4 仿真測試及分析

4.1 算例與參數設置

為了驗證算法的可行性，本文用Matlab對柔性車間調度進行實例分析，選取同一個算例將離散布谷鳥算法（DCS）與改進遺傳算法（GA）和改進混合粒子群算法（PSO）進行對比。6個工件在10臺機器上加工，每個工件都要經過6道工序，每個工件的每個工序可選擇機器和對應機器所需加工時間已確定，如表1所示。

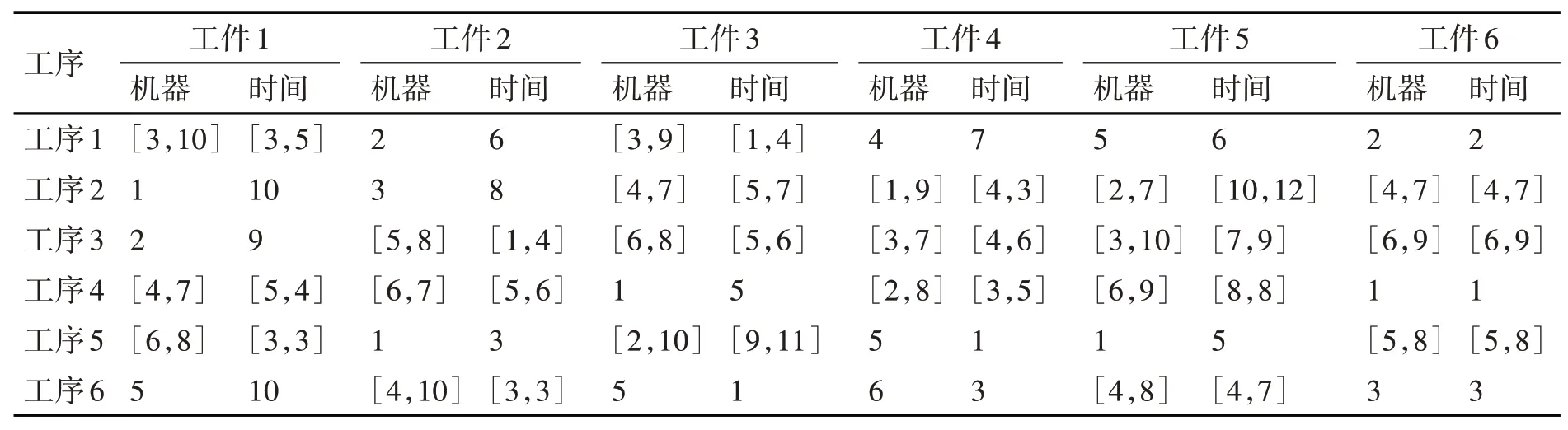
表1 加工機器選擇和對應加工時間

4.2 算法結果分析和對比

本文采用Matlab R2018a編程，運行環境為In?tel（R）Xeon（R）CPU E5-@3.30GHz，RAM 8GB。為了方便DCS、GA和PSO算法對比，三種算法設置相同的主要參數，個體數目為40，最大迭代次數為50。同時三個算法的其他參數都調到最優。為了避免結果的隨機性，每組算法獨立運行30次，分別記錄其最優值Cbest、平均值Cavr、標準差Cstd和方差Cvar測評算法的性能，最后運行結果如表2所示。經過30次獨立運算和比較，DCS算法最穩定，不容易陷入局部最優；而PSO算法和GA算法，雖然也能得到最優，但是產生的解并不穩定，隨機性比較高。

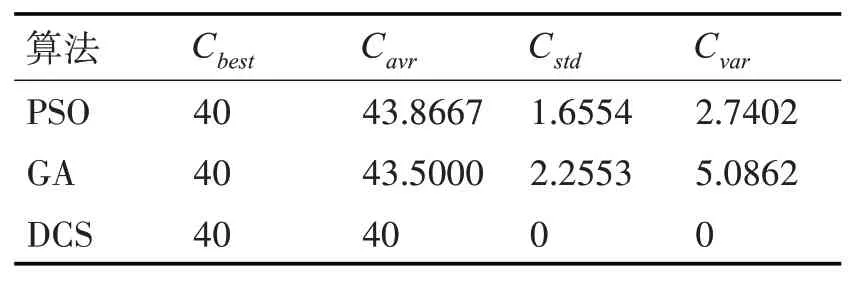
表2 算法對比實驗結果

圖6 為迭代曲線圖，如圖7為DCS算法求解得出的工件加工甘特圖。圖6直觀地對比了迭代過程中DCS、GA和PSO算法關于柔性車間問題的最短調度時間，曲線的起點為各個算法隨機產生的初始種群中的最優值，由于初始種群是隨機產生的，導致各個算法的初始最優解相差較大，隨著迭代次數的增加，種群個體逐漸趨向于最優。可以看出，DCS算法不僅得到的解更優，收斂速度也更快并且不容易陷入局部最優。

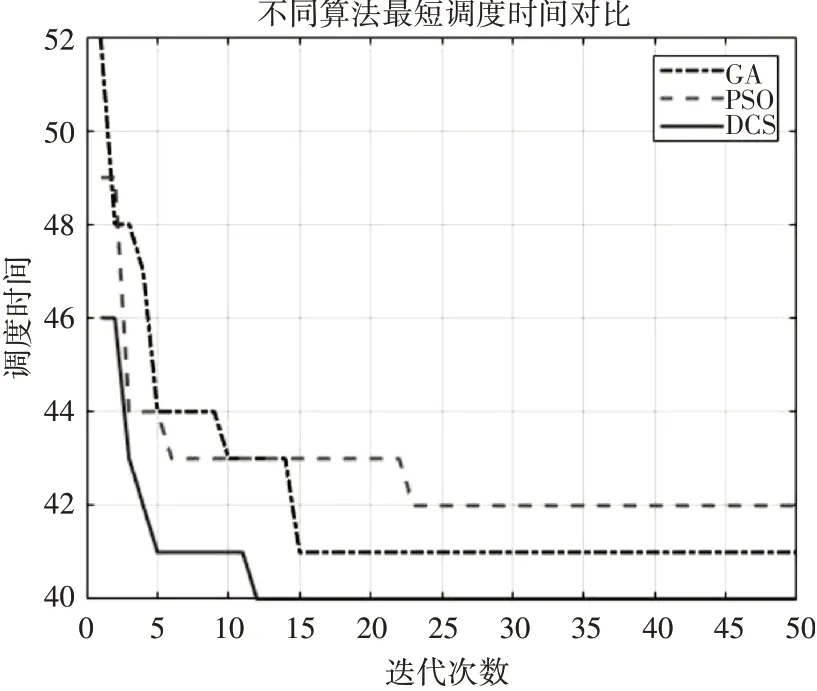
圖6 進化曲線圖

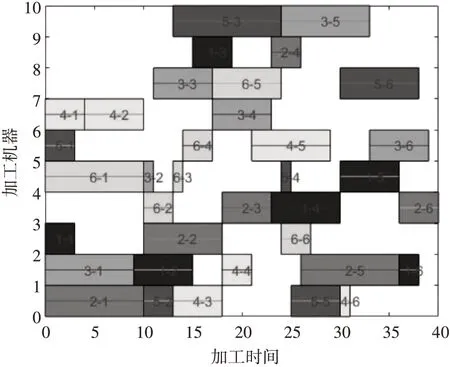
圖7 工件加工甘特圖

5 結語

本文研究了以最小化最大完工時間為目標的柔性車間調度問題，建立了基于各個工序最早完工的調度模型，提出了離散布谷鳥算法求解該問題，并且采用雙層整數編碼方法對個體進行編碼，將后續步驟簡單化。最后通過對比試驗，驗證了本文采用的離散布谷鳥算法的可行性和穩定性。在此基礎上，以完工時間、流水時間和延遲時間等多目標的改進FJSP求解將是進一步的研究目標。