基于自適應粒子群的SVM參數優化研究?

姜雯吳陳

（江蘇科技大學計算機學院 鎮江212000）

1 引言

支持向量機（Support Vector Machine，SVM）是Cortes和Vapnik于1995年提出的，SVM在解決小樣本，非線性以及高維模式識別中有著顯著的優勢［1~3］。在支持向量機模型中，懲罰因子C和核參數γ是影響分類結果的主要因素［4］。人工智能算法為啟發式算法，即不用去遍歷解空間里的所有位置，就可以尋找到問題的最優解，因此能夠高效地尋找到最優的SVM參數。傳統的人工智能算法有遺傳算法［5］、粒子群算法［6］、蟻群算法［7］等。本文采用粒子群算法來優化SVM參數，從而提高SVM的分類性能。粒子群算法是一種基于種群的全局優化方法，具有算法簡單，易于實現以及收斂速度快的優點。由于粒子群算法在演化過程中很容易過早收斂并陷入局部最優，目前已經有很多學者提出對粒子群算法進行優化［8~11］。針對傳統的粒子群算法在優化支持向量機時存在著易陷入局部最優，分類精度低以及早熟收斂的缺點，本文采取兩種方式對粒子群算法進行優化，利用改進后的算法找到最優SVM參數，提高SVM的分類精度。

2 支持向量機

支持向量機的原理是建立一個最優分類超平面，使得該超平面在正確分開不同類別的樣本的同時，還能使得分類間隔最大化。假設訓練樣本集為

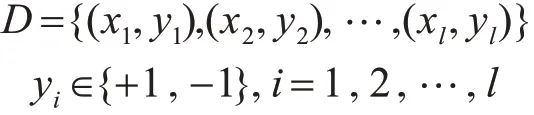
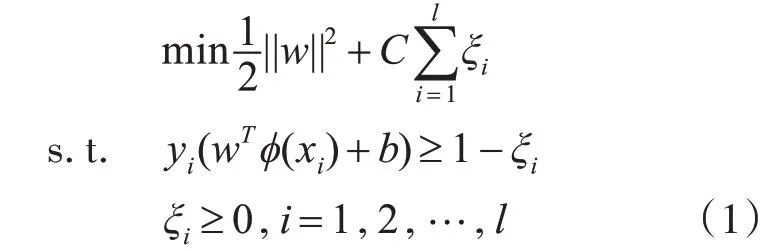
可求得最優分類超平面為其中，w為超平面法向量；ξi為松弛因子；C為懲罰因子；xi為第i個樣本的特征；yi為類別標簽；φ（xi）為映射函數；

利用Lagrange函數，可得到該問題的對偶形式：

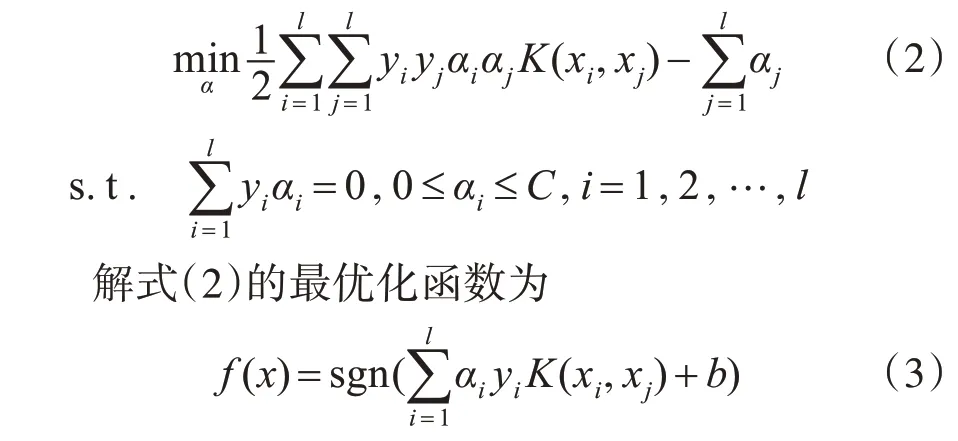
其中，αi為Lagrange乘子；K(xi，xj)∈Rn為核函數，本文采用高斯核函數［12］作為SVM模型中的核函數，其數學形式為

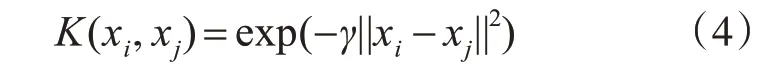
其中，γ為核參數。

3 對粒子群算法進行優化

3.1 經典粒子群算法

粒子群算法是由Eberhart和Kennedy在1995年提出的一種群智能優化算法，它是源于對鳥類覓食行為的研究。粒子群算法具有收斂速度快，算法簡單以及效率高的優點。在粒子群算法中，每個粒子具有位置和速度兩個屬性，粒子的位置表示某個可行解，粒子的速度則表示與下一個可行解的差值。每個粒子可以根據已經尋找到的最優解和整個粒子群的最優解不斷調整自己的速度，以此來尋找到更優的解。

假設所求解問題的空間是d維，種群大小為m，種群中的每個粒子代表一個可行解，則第i個粒子的位置和速度分別為Xi=(xi1，xi2，…，xid)和Vi=(vi1，vi2，…，vid)。記第i個粒子經過的最好位置為Pbest=(ppbest，1，ppbest，2，…，ppbest，d)，整個種群經過的最優位置為gbest=(pgbest，1，pgbest，2，…，pgbest，d)。在迭代過程中，粒子可通過個體極值pbest和群體極值gbest來進行更新自己的速度和位置，即：

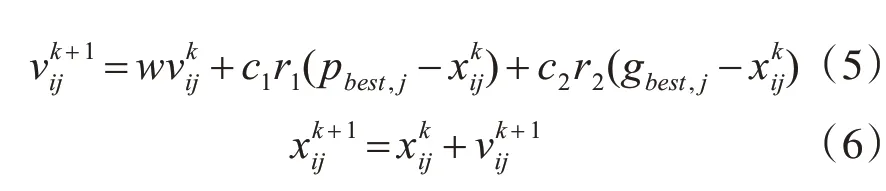
其中w為慣性權重；c1，c2為學習因子，為常數；r1，r2為［0，1］區間內的隨機數；k為進化的代數，1≤i≤m，1≤j≤d。

3.2 改進慣性權重的粒子群優化算法

在粒子群算法中，慣性權重w的大小影響粒子群算法尋找最優解的能力［13~14］。若w較大，則有利于提高粒子的全局最優能力，使得算法跳出局部最優點；若w較小，則會提高粒子的局部最優能力，使得算法趨于收斂。本文采用自適應權重來取代慣性權重，從而平衡粒子的全局和局部最優能力：

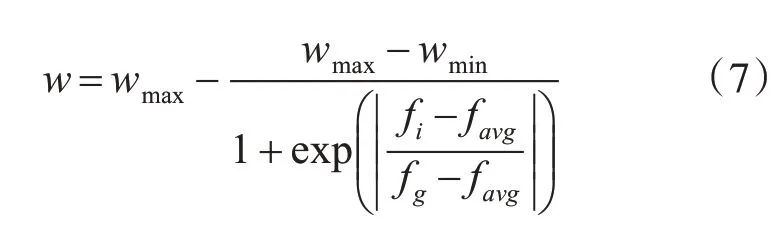
其中，wmax為權重的最大值，wmin為權重的最小值，通常取wmax=0.9，wmin=0.4；fi為第i個粒子的適應度值，favg為種群平均適應度值，fg為種群最優適應度值。

3.3 引入自適應變異的粒子群優化算法

本文將粒子群中的每個粒子位置變量設定為二維，兩個分量為x(i，1)和x(i，2)。其中，x(i，1)的范圍為(Cmin，Cmax)，x(i，2)的范圍為(γmin，γmax)，分別對應SVM的懲罰因子C和核參數γ，用粒子的適應度值來評價粒子所處位置的好壞程度。

本文采用自適應變異對粒子群算法進行優化，賦予部分粒子一定的變異概率，從而增強粒子的種群多樣性［15~16］，在一定程度上跳出局部最優解，達到全局最優。具體變異算法如下：

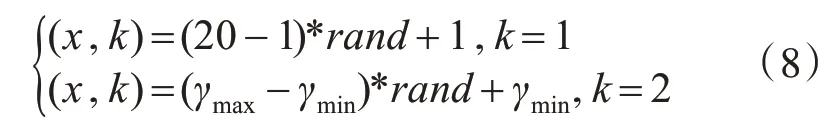
其 中，k=ceil(2*rand)，rand的 范 圍 為(0，1)，

改進后的粒子群算法具體步驟如下：

步驟1：初始化PSO的相關參數。在一定范圍內隨機生成粒子的初始位置。

步驟2：計算粒子的適應度值。利用臺灣林智仁教授開發的LIBSVM工具箱里的svmtrain函數來計算各個粒子的適應度值。將每個粒子的位置分量x(i，1)和x(i，2)代入適應度函數中得到適應度值，計算過程如下：

教學的意義在于使學生擁有終身發展，并且適應社會的知識儲備以及能力。利用網絡的發展與高中物理教學相結合，能夠有效提升學生對于社會科技發展的敏感度，這對于學生個人未來發展具有重要意義。同時，多樣化的網絡技術也產生了各具風格和內涵軟件平臺，可以有效改善一些現實的限制，諸如試驗的設備等，也可以增強教師與學生和家長的聯系，使教學活動范圍從局限于學校，到建立真正的學校家庭學習體系，更重要的是教師可以從新利用這些平臺，實現對學生多方面能力的綜合培養。

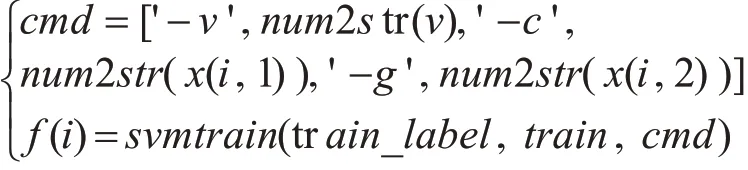
其中，v表示交叉驗證數，c表示懲罰因子C，g表示核參數γ，f(i)表示第i個粒子在當前位置的適應度值，算法中用fi表記。train_label表示訓練數據集標簽，train表示訓練數據集。

步驟3：根據粒子初始適應度值，可得到粒子的個體極值pbest和群體極值gbest。

步驟4：根據式（7）更新權重；根據式（5）和式（6）更新粒子的速度和位置。

步驟5：根據式（8），對部分粒子進行變異。

步驟6：計算粒子當前適應度值，并更新粒子個體極值pbest和群體極值gbest。

步驟7：判斷是否達到最大迭代次數，若滿足則轉至步驟7，否則轉至步驟2。

步驟8：輸出種群最優位置（對應SVM的懲罰因子C和核參數γ）。

步驟9：輸入最佳SVM參數，進行分類。

4 實驗結果與分析

本文采用UCI標準數據集（Seeds，Wine，Iris）對改進的算法進行驗證分析。其中，實驗參數設置如下：在SVM中，懲罰因子C的范圍為0.1~100，核參數γ的范圍為0.01~10；在粒子群算法中，進化次數為200，種群數目為20，學習因子C1=1.5，C2=1.7，慣性權重wmax=1.5，wmin=1.7。

Seeds數據集有三個類別，共計210個樣本。每個類別有70個樣本，將每個類別隨機抽取40組作為訓練集，30組作為測試集，測試集共計90組。分別用PSO-SVM和本文改進的算法GPSO-SVM進行試驗，實驗結果如表1所示。實驗結果表明，改進后的算法（GPSO-SVM）可糾正5個錯分樣本，分類精度提高了5.56%

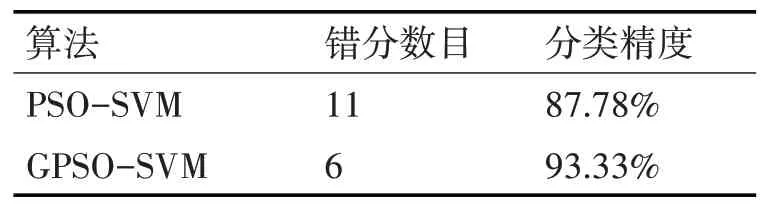
表1 Seeds數據集實驗結果

Wine數據集一共有三個類別，共計178個樣本。隨機抽取108組作為訓練集，70組作為測試集。實驗結果如表2所示。實驗結果表明，改進后的算法（GPSO-SVM）可糾正5個錯分樣本，分類精度提高了7.14%。

表2 Wine數據集實驗結果

Iris數據集一共有三個類別，共計150個樣本。將每個類別隨機抽取30組作為訓練集，剩下來的作為測試集，測試集共計60組。實驗結果如表3所示，實驗結果表明，改進后的算法（GP?SO-SVM）可糾正4個錯分樣本，分類精度提高了6.67%。

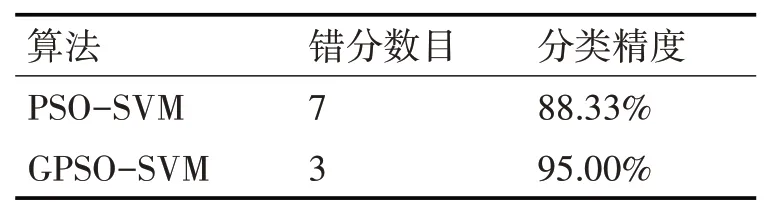
表3 Iris數據集實驗結果

實驗結果表明，改進后的算法的分類精度明顯優于PSO-SVM算法，改進后的算法不僅能有效地避免粒子陷入局部最優，更增強了粒子的種群多樣性，具有較高的分類精度。

5 結語

本文針對粒子群算法在優化支持向量機分類時易陷入局部最優，早熟收斂的問題，利用自適應權重和引入自適應變異對粒子群算法進行改進，使得粒子的全局搜索能力和局部搜索能力能夠達到良好的平衡，從而達到全局最優。本文使用UCI標準數據集對改進后的算法進行實驗論證。實驗結果表明，改進后的算法提高了算法的分類性能。在今后的研究中，不僅要尋找更好的改進方法來優化粒子群算法，更要從效率和精度兩方面提高分類的性能。