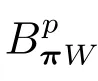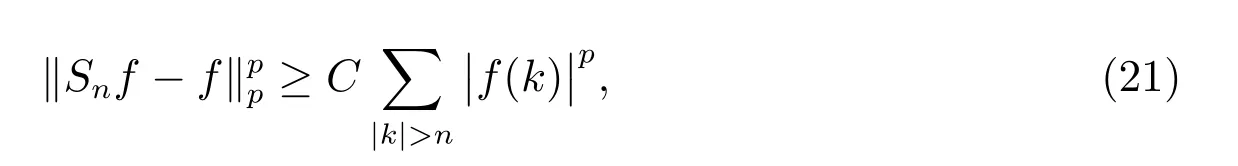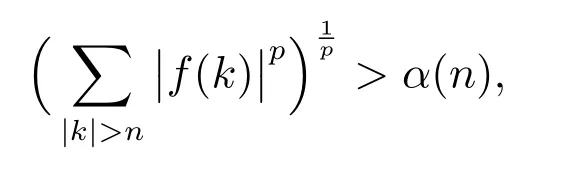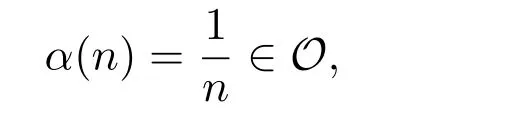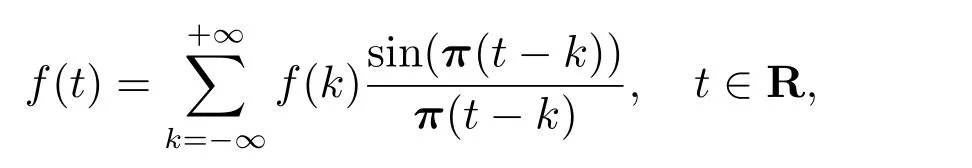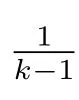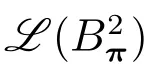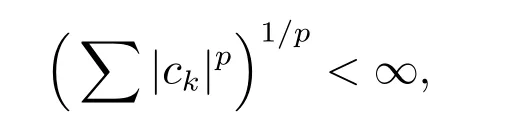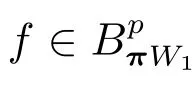過采樣技術下Shannon采樣重構的任意慢收斂
武 瑛, 高萌瑤, 張雪林
(1-西安科技大學理學院,西安 7 10054;2-陜西師范大學數學與統計學院,西安 7 10062)
1 引言
Shannon采樣定理是信號重構理論的基礎,并已成為通信工程和信息論中最重要的數學技術之一.與此同時該定理也滲透了許多物理和工程分支,如信號分析、圖像處理、雷達、聲納、聲學、光學、全息、氣象學、海洋學、晶體學、物理化學、醫學成像等等[1].該定理具有悠久的研究歷史,曾被多位學者獨立研究發現.最早于1915年由Whittake在數學文獻中做出闡述[2],而后Kotel’nikov于1933年在工程文獻上發表了采樣定理的相關文章[3].1948年Shannon利用采樣定理證明了模擬帶限信號在信息意義上等價于其按Nyquist速率采集的樣本級數[4].因此,它也被稱為Nyuist-Shannon采樣定理和Whittaker-Kotel’nikov-Shannon采樣定理,并作為插值理論中的基本定理.Shannon采樣定理闡述了用離散樣本重構連續信號的方法,具體來說它主要分析了兩個問題:第一,哪類具有有限能量的連續時間信號,可以通過僅使用等距離采樣來做出唯一地表示;第二,如何進行重構.關于更詳盡的相關解釋建議參考文獻[5].在數學上,這個定理描述如下.
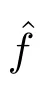
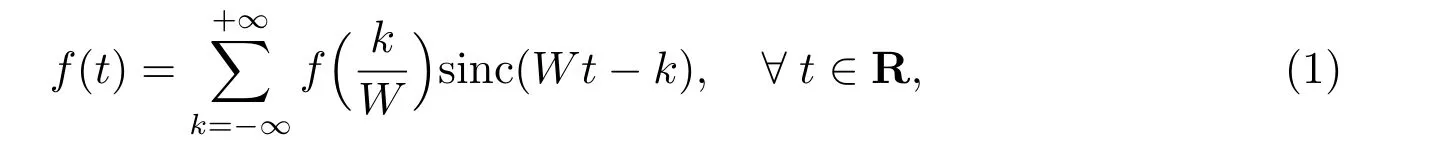
其中
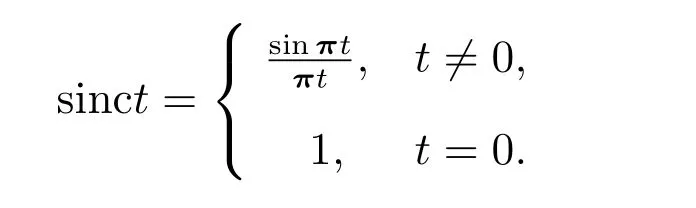
前人已經對(1)中主級數的收斂速率進行了廣泛研究.原始的研究致力于采樣定理在每一個點t∈R處的點點收斂,并證明了該主級數在R的每一個緊支集上是一致收斂的.此外,文獻[6]證明了主級數依L2范數收斂到信號f,即

在p=2時成立.當1 理論上來說,要得到精確的重構就需要無限多的樣本.然而在實際應用中,只能獲得有限個樣本,這也就勢必造成了所謂的截斷誤差.一般地,信號f的n階截斷誤差定義為 其中Sn是n階有限維重構算子,定義為 截斷誤差可以根據采樣率和范數來估計,然而這些估計總是需要某些函數類內信號的先驗界,并且一般不適用于帶限信號.因此,盡管可以得到某些信號的收斂速率,但是對于所有帶限信號,其收斂速率慢的程度依然無從估計. 眾所周知,過采樣可以加速重構序列的收斂.具體來說,過采樣是對[?πW,πW]上的帶限信號采用更高的采樣率?W>W來采取樣本.在文獻[9]中,作者證明了用過采樣技術后,對于p=∞,(2)式全局一致收斂.然而,對于一般的帶限信號,收斂速率依然是未知的.在文獻[10]中,作者證明了應用過采樣并認真選擇重構基底函數后,在局部有界區間上收斂速度能夠達到指數收斂.這也為實際應用中只能選取有限個樣本的情況提供了更好的重構方法. 正是由于重構收斂速率的慢,和對于所有帶限信號而言的收斂速率有多慢的未知性,在一定程度上影響了采樣重構理論的實際應用.因此,研究重建的收斂速度有多慢,在理論上是有意義的.此外,在文獻[11]中討論了收斂速率有多慢,并且遺留了關于加速技術下的重建算子序列是否仍然是“任意慢”的問題.根據于本文的研究成果,也對上述遺留問題做出了回答,即加速技術并沒有為慢收斂帶來改善. 在本文中,作者應用算子列的慢收斂理論,從重構算子序列Sn的角度來分析香農重構的收斂速率.文章的主要結論見第3節,作者證明了重構算子序列Sn“任意慢”地收斂到恒等算子.具體來說,當1 設Lp(R),1≤p<∞,是所有R上p次冪Lebesgue可積信號的函數空間,其中Lp定義為 對于σ>0,Bσ是所有復平面C上整函數的函數空間,其整函數需滿足如下性質:對任意的ε>0,存在一個常數C(ε),使得 文獻[12,13]中Banach空間的算子序列慢收斂理論,提供了描敘線性算子序列強收斂的定量方法.令O是收斂到0的所有遞減正序列的集合,即 X和Y是同一個標量域上的兩個賦范線性空間,且將L(X,Y)定義為所有從X到Y的有界線性算子構成的賦范線性空間.當X=Y時,L(X,Y)簡化為L(X).對于序列{Ln}?L(X,Y),該序列強收斂到L∈L(X,Y),即 文獻[12]中給出任意慢收斂的定義如下. 定義1 對于任意α∈O,若存在x=xα∈X,使得 ‖Ln x?Lx‖Y≥α(n),?n∈N, 則稱序列{Ln}任意慢收斂到L. 以下兩個定理是本文所用到的結果.其中定理2意味著滿足一定條件時,一個強收斂到恒等算子的有界線性算子序列實際上是任意慢收斂的.定理3是對經典Bernstein嗜睡定理的概括,它為后續任意慢收斂的證明提供了啟發和理論支撐.我們先列出定理[14,15]. 定理2 設Fn是從Banach空間X到它自身的映射序列,且使得 則有下列敘述等價: 1)Fn強收斂到恒等算子I; 2)Fn任意慢收斂到恒等算子I; 3)Fn幾乎任意慢收斂到恒等算子I. 定理3 設{0}=L0?L1?L2···是Banach空間X的有限維閉子空間序列,Y是X的無限維閉子空間.那么對于任意α∈O,存在y?∈Y,使得 下述定理說明了重構算子序列{Sn}在奈奎斯特速率下的收斂速度. 證明 由Sn的定義可知,對任意的n∈N,Sn都是有限維的,即 故根據已知等式(8)和定理2可知,Sn強收斂到恒等算子I且Sn任意慢地收斂到恒等算子I. 其中 W3=W2+δ>W2>W1. 下述定理也是本節內容的主要結果之一. 為了證明定理6,我們需要來自文獻[17]中的引理如下. 由引理1,我們有 根據(11)和(12)式可得,對于任意m,有 于是,由(15)和(16)式,可得 因為m=k時sinc(m?k)=1,m?=k時sinc(m?k)=0,所以(17)式右邊的雙求和可簡化為對滿足m=k的m和k求和,這里使用k作為求和指標,我們有 再次利用引理1,級數 是收斂的,即意味著隨著n→0, 其中C僅依賴于p和W.我們可以構造出信號f使得該信號滿足 即說明奈奎斯特速率下重構算子序列是任意慢收斂的.以p=2為例,對收斂速度很慢的 構造信號f為 ε=(c?∞,···,c?1,c0,c1,···,c∞), 其中 該數列ε的余項收斂到0也是任意慢的.
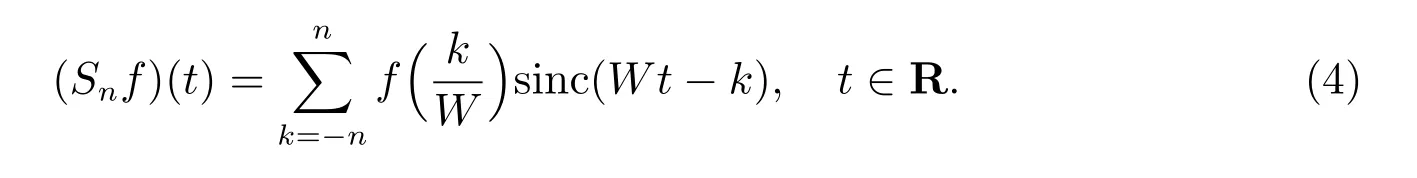
2 預備知識
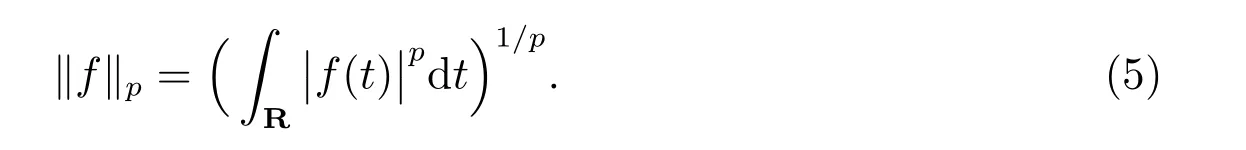
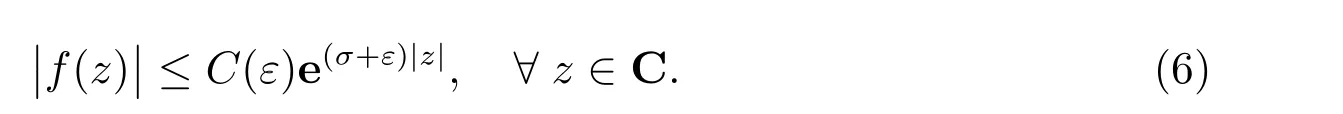


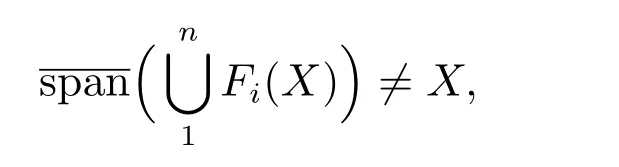
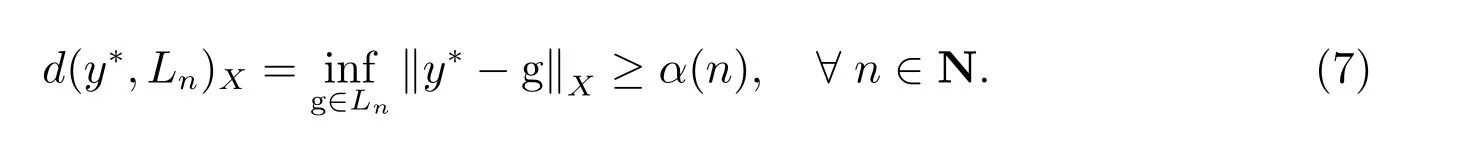
3 重構算子序列的收斂速度
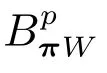
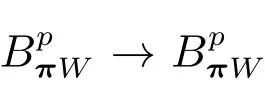

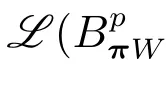

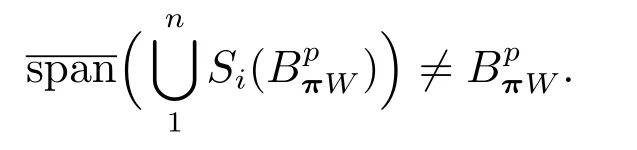
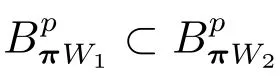
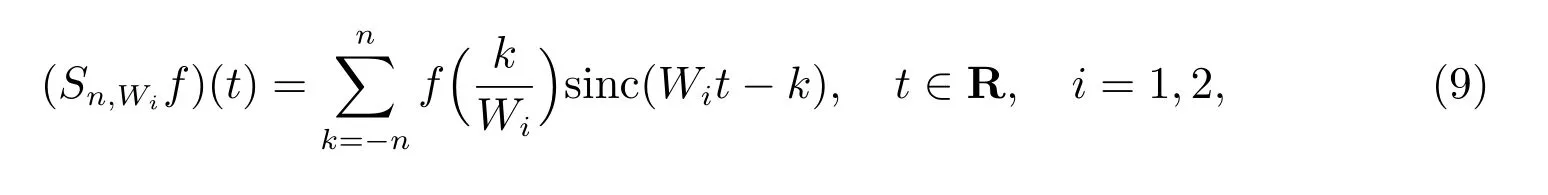

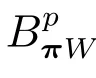
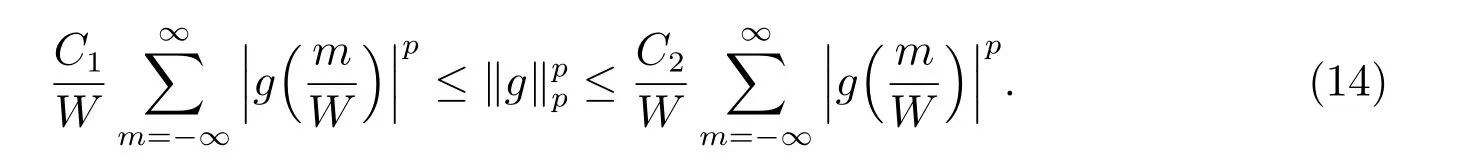

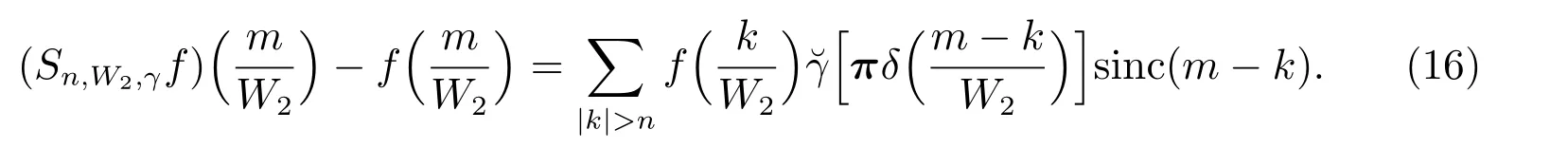
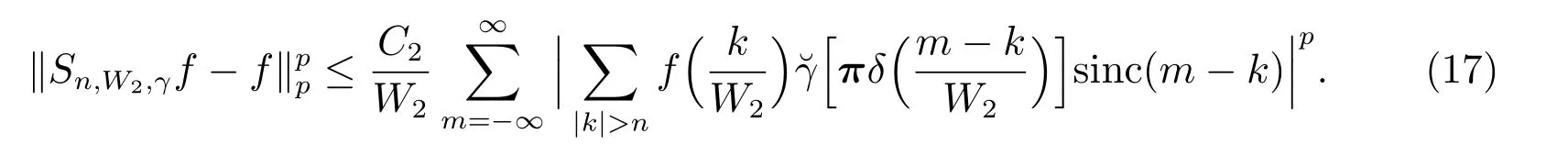
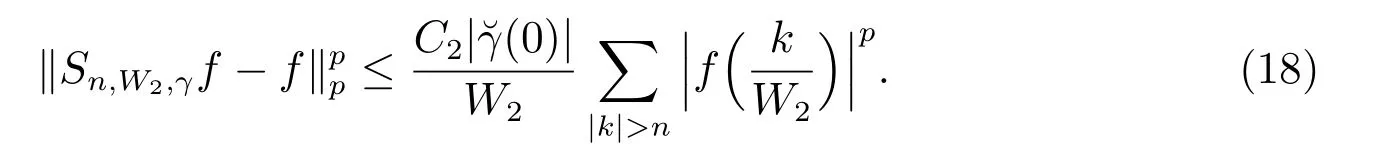
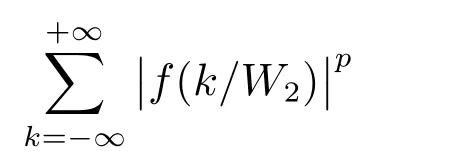

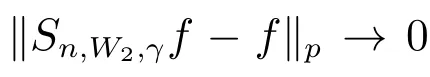


4 結論與應用