變系數空間自回歸模型的Bootstrap檢驗

杜 穎, 李體政

(1-西安外國語大學經濟金融學院，西安 7 10128;2-西安建筑科技大學理學院，西安 7 10055)

1 引言

近年來在對經濟等領域問題的研究分析過程中，發現如犯罪率、社會互動、經濟增長、溢出效應、同伴效應、價格競爭、稅收競爭、房價、地價等重要的經濟指標中普遍存在著空間相關性，而線性空間自回歸模型是描述空間相關性的最經典和最流行的模型之一.有關模型的估計、統計推斷及應用等方面的問題得到了深入研究[1-3].一方面由于線性空間自回歸模型對回歸函數的假設過于嚴格，當回歸函數的設定不準確時就會產生很大的估計偏差，甚至可能會得到錯誤的結論.另一方面線性空間自回歸模型忽略了空間數據中可能存在的動態特征，即響應變量與協變量之間的關系會隨著某個變量(比如年齡、受教育程度、收入水平等)的變化而變化，因而不能有效處理具有動態特征的空間數據.針對上述問題，李坤明和陳建寶[4]通過假定線性空間自回歸模型中的回歸系數是某個協變量的未知函數，提出了變系數空間自回歸模型，其形式如下

變系數空間自回歸模型假定經典線性空間自回歸模型中的常數回歸系數為其他解釋變量的未知函數，增加了模型的靈活性和適應性，同時由于系數函數通常被看作是某個自變量的一元函數而有效避免了擬合中因自變量維數增加而造成的維數災難問題.更重要的是由于模型中的系數函數隨著某個協變量的變化而變化，從而使得該模型能夠有效挖掘空間數據中的動態特征.在實踐中，模型(1)中的一些系數函數可能是常數，而其他系數與解釋變量u有關.在這種情況下，模型(1)可以進一步簡化為空間計量經濟學中的半變系數空間自回歸模型.從估計的角度看，半變系數空間自回歸模型不能簡單認為是變系數空間自回歸模型的特殊情況，因為將常系數視為變系數會導致估計效率的損失.對于半變系數空間自回歸模型，Wei等[5]提出了一種輪廓擬最大似然方法，該方法利用局部線性平滑法估計變系數，利用擬最大似然法估計常系數.Sun[6]也建立了一個基于半參數序列的最小二乘法估計方法分別估計變系數和常系數.盡管半變系數空間自回歸模型的建立能更全面真實地描述響應變量與協變量之間的關系，但在實際應用中，我們首先應明確哪些回歸系數可以假定為常數，僅憑對實際問題背景的了解做出符合實際的假設在很多情況下是困難的，甚至是不可能的，這就需要系統地檢驗變系數空間自回歸模型中哪些系數函數是常數，解決這個問題將為半變系數空間自回歸模型的確定提供理論依據.本文建立了一種確定變系數空間自回歸模型中部分系數函數是否為常數的Bootstrap檢驗方法，利用在備擇假設和零假設下關于系數擬合值的輪廓擬對數似然函數的差值構造了檢驗統計量，并且通過模擬實驗考察了Bootstrap方法逼近其零分布的有效性以及統計量的檢驗功效.

2 變系數空間自回歸模型及其輪廓擬最大似然估計方法

由于估計方法是檢驗的基礎，在討論參數的統計推斷問題之前，我們先簡單回顧一下變系數空間自回歸模型的輪廓擬最大似然估計方法.

對于模型(2)，文獻[4]給出一種兩步估計方法.

第1步 固定ρ，并整理模型(2)，可得

其中Y(ρ)=T(ρ)Y.設β1(·),β2(·),···,βq(·)具有連續的二階導數，則對任一給定的u0∈U，變系數模型的局部線性擬合為選擇β(u0)，使

這里Yi(ρ)是Y(ρ)的第i個分量，Kh(·)=K(·/h)/h，其中K(·)為給定的核函數，h為窗寬.

因此，求上述局部加權最小二乘問題的解可得到系數函數向量β(u)在u0處的局部線性估計

其中0q×q表示q×q零矩陣，

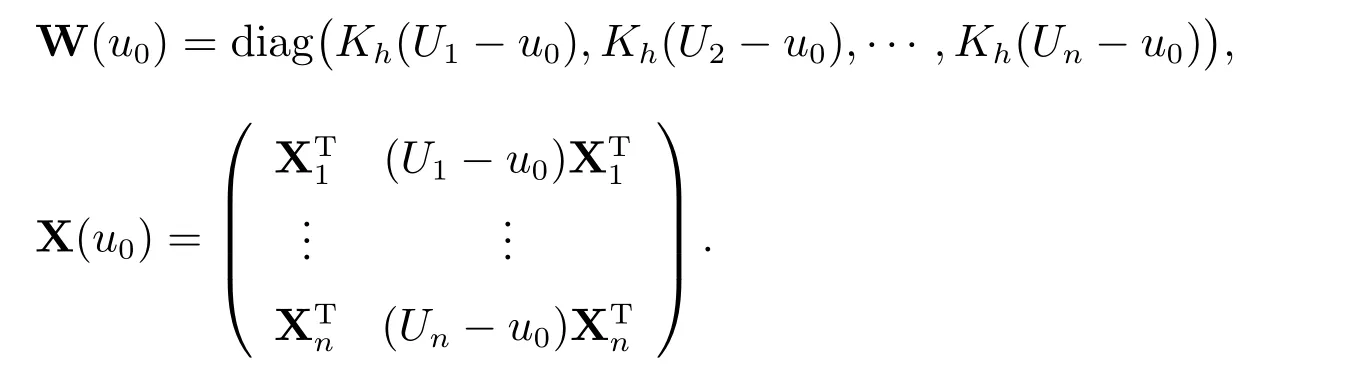
特別地，分別取u0=U1,U2,···,Un，對于給定的ρ，可得

其中

第2步 最大化下面的輪廓擬對數似然函數

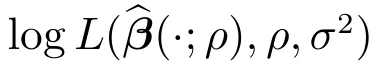
其中M1=(In?S)T(In?S).進而將結果帶入式(7)中得到

3 基于殘差項的Bootstrap檢驗

如前所述，對于變系數空間自回歸模型，通常人們感興趣的問題為，是否其中的某些系數可視為常數，因而有如下的假設

其中{i1,i2,···,ir}是{1,2,···,q}的一個非空子集，βi1,βi2,···,βir為未知常數.

3.1 檢驗統計量的構造

本小節中，針對上述假設，我們給出由在備擇假設和零假設下關于系數擬合值的輪廓擬對數似然函數的差值所構造的似然比檢驗統計量.

在假設H1下，按照第2節介紹的方法擬合變系數空間自回歸模型，可得到輪廓擬對數似然函數在此估計下的值

在假設H0下，模型(1)變成如下的半變系數空間自回歸模型

其中

Ic={i1,i2,···,ir},Ic∪Iv={1,2,···,q},Ic∩Iv=φ.

下面通過簡單介紹文獻[5]的輪廓擬最大似然估計過程與結果來計算相應的半變系數空間自回歸模型的對數似然函數值.首先，固定βc和ρ，并將模型(14)寫成如下形式

根據文獻[7]的局部線性光滑方法可以得到模型(15)中的系數函數的估計值，因而，對于給定的βc和ρ，可以得到Mv的估計值

其中

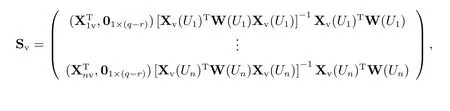
然后，對于任一給定的ρ，找到βc和σ2，使得

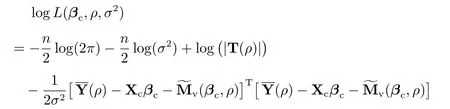
的值最大.求解上述問題可得βc和σ2的輪廓擬最大似然估計值如下

其中

則假設(11)下的似然比檢驗統計量為

其中當T過分偏大時，應拒絕H0.設t為T的觀測值，則檢驗的p值為

上述統計量經常被用來比較兩個相關模型之間的擬合優度問題[5,8,9].如果不考慮空間相關性取ρ=0，則檢驗統計量即為經典的廣義似然比檢驗[10]，并被廣泛用于各種非參數和半參數回歸模型的推斷問題[11].Fan和Huang[12]指出用廣義似然比檢驗方法進行假設檢驗時，除了原假設中模型的參數估計過程不需要選擇窗寬的情形，其它情形在對零模型和備擇模型的估計過程中應該選擇相同的窗寬，否則窗寬的變動可能會使得零模型和備擇模型的對數似然函數之間無法比較，從而導致檢驗成效的損失.此外，Fan和Jiang[11]以及Cai[13]提出，對于給定的數據集，由于原假設中的模型設定不確定是否正確，應該使用備擇假設中擬合的結果來生成Bootstrap取樣所需要的殘差值.基于這兩點考慮，本文在構造檢驗統計量(21)時，使用變系數空間自回歸模型選出的窗寬對半變系數空間自回歸模型進行擬合.

3.2 計算p值的Bootstrap方法

在計算統計推斷的p值時，尋求檢驗統計量的零分布是首先要解決的重要問題.然而，由于模型中存在空間滯后項，使得檢驗統計量零分布很難精確得到.即使這個漸近分布能夠得到，Fan和Jiang[11]指出在有限樣本容量下有可能會導致錯誤的推斷結果.眾所周知，Bootstrap方法是一種非常有效的模擬統計量分布的再抽樣方法，已被廣泛應用于各種統計推斷問題中[14,15]，也是本文用以逼近檢驗統計量零分布的方法.

因而，關于p值的計算，由如下的Bootstrap方法實現：

其中

其中#A表示集合A中元素的個數.

3.3 有關Bootstrap檢驗方法的討論

1) 此方法可用于全局回歸關系平穩性檢驗，可以檢驗所有的系數函數均為常數的假設，即驗證經典的線性空間自回歸模型是否適用于所給的樣本數據.此時原假設變為

H0:模型(1)中所有系數均為常數,

對應的是經典的線性空間自回歸模型

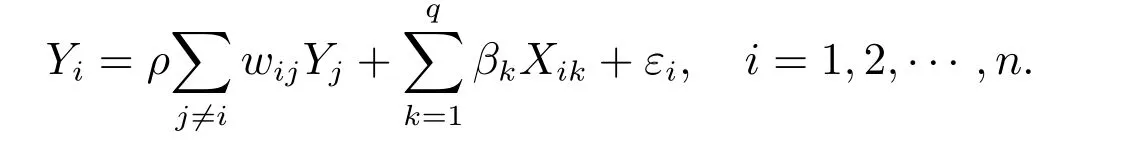
在此情形下，上述的零模型很容易由擬最大似然估計法來擬合.

2) 此檢驗方法可以進一步推廣.盡管我們所構造的Bootstrap方法是用來確定變系數空間自回歸模型中的常系數的，它還可以用于檢驗系數函數更復雜的結構.其中一個自然推廣為檢驗一些系數是否為自變量u的一些已知函數的線性組合.對應的原假設為

這里對每個k∈{i1,i2,···,ir},θkl(l=1,2,···,Ik)為未知參數，fkl(u)(l=1,2,···,Ik)為已知的相互獨立的，自變量u的線性函數，則原假設中假定部分系數是線性的或者是u的廣義多項式函數均可以看作是(25)的特殊情形.在原假設下對應的模型為

若令

Zikl=fkl(Ui)Xik,l=1,2,···,Ik,k=i1,i2,···,ir,i=1,2,···,n,

則零模型可以進一步表示為

由于Zikl(l=1,2,···,Ik,k=i1,i2,···,ir,i=1,2,···,n)是已知的，故上述模型也是半變系數空間自回歸模型.因而，所構造的檢驗方法可用于檢驗原假設(25).

檢測方法的另一個推廣是對一個半變系數空間自回歸模型與另一個半變系數空間自回歸模型之間的假設進行檢驗.在這種情況下，備擇模型是一個半變系數空間自回歸模型，原假設對應的模型可以有多種選擇.例如，為了評估備擇模型的常系數部分中的一些解釋變量是否確實影響了響應變量，可以相對應的設置一個假定這些解釋變量對應的系數均為零的原模型.

4 模擬試驗

本節通過模擬試驗考察Bootstrap方法的有效性，在觀測值來自正態和非正態總體時分別考察檢驗方法逼近檢驗統計量零分布的精確性以及檢驗的功效.由于解釋變量存在共線性會影響系數估計的結果，我們也考察了解釋變量間共線性的存在對檢驗性能的影響.

4.1 試驗設計

在試驗中，在由l×l個方塊組成的格點處選取觀測值，這樣樣本容量為n=l2.空間權重矩陣W設為Queen矩陣.用以產生數據的變系數空間自回歸模型為

這里wij表示W的(i,j)分量，Xi1≡1,Ui為產生于均勻分布U(0,1)的隨機變量，(Xi2,Xi3,Xi4)T(i=1,2,···,n)為產生于N(0,Σ)的隨機變量(其中Σ的主對角線元素為1，其它元素取值為γ).為了全面考察解釋變量X2,X3以及X4之間的共線性程度對檢驗方法的檢驗效果帶來的影響，我們分別選取γ為常數0,0.5和0.8以及

四種情形.同時為了考察空間相關性對檢驗的影響，空間滯后相關系數ρ取值為?0.9,?0.6,?0.3,0,0.3,0.6以及0.9.系數函數β1(u),β2(u),β3(u)以及β4(u)的選取如下

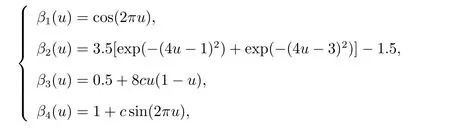
這里c是一個常數，通過對c的不同取值來評價檢驗的功效.注意，當c=0時，表示H0為真，而c?=0時，表示H1為真，且H1與H0之間的偏差會隨著c的絕對值的增加而增加.

為了考察誤差項對檢驗方法有效性的影響，我們同時給出了下面四種常見的誤差分布情況下的模擬結果：

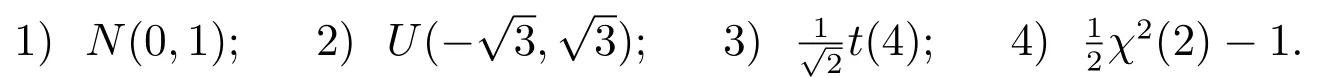
模擬中采用Gaussian核函數

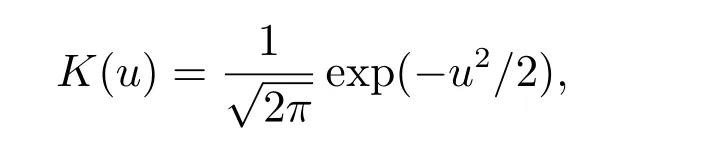
窗寬選擇根據文獻[5]采取ROT方法.

4.2 模擬結果分析

針對樣本數n=102和n=132，ρ的七種不同取值，γ的四種不同取值以及四種不同的誤差分布組合的每一種設定情形，重復試驗N=500次，且每一次試驗都將進行500次Bootstrap抽樣模擬來計算統計量的p值.

1) Bootstrap方法逼近零分布的有效性

令系數函數β3(u)和β4(u)中的c=0，此時H0為真且β3(u)=0.5,β4(u)=1，則在原假設條件和每一種設定情況下，我們計算500次重復下的p值分別小于給定的不同顯著性水平(即拒絕H0)的頻率，其中p值是基于500次Bootstrap模擬計算得到的.擬合的結果展示在表1中.

表1 在Bootstrap檢驗拒絕H 0的頻率

續表1 在Bootstrap檢驗拒絕H0的頻率

由表1的結果可知，當H0為真時在所有的試驗設定下，拒絕H0的頻率非常接近于給定的顯著性水平α的值.也就是說，即使在較小樣本n=100時，Bootstrap方法都可以精確地逼近統計量T的零分布.我們發現不管是在正態的誤差分布還是非正態的誤差分布下，模擬結果沒有明顯差別，這表明對統計量T的零分布的Bootstrap逼近的表現對誤差項的分布是穩定.同樣，空間自相關參數ρ和解釋變量之間共線性也沒有表現出明顯影響拒絕H0的頻率的結果的情況.這些都說明了Bootstrap方法逼近零分布的有效性.

2) 統計量的檢驗功效

當c?=0，則假定所有系數都是變系數的備擇假設為真.在這種情形下，我們將β3(u)和β4(u)中的c分別取值為0.1,0.2和0.3.在顯著性水平α=0.05下，分別計算N=500次重復下拒絕H0的頻率，并以此模擬檢驗功效.擬合的結果展示在表2中.

由表2可以看出，隨著樣本容量的增加或者c的增加即備擇假設與原假設模型之間的偏差加大，檢驗功效是逐漸增大趨近于1的，這表示所用的檢驗方法具有良好的檢驗功效性質.由表2，我們發現檢驗方法的表現對于我們所考察的四種正態和非正態情形下的誤差分布，以及七個不同取值的空間滯后相關系數ρ，并沒有出現太大的差異，說明檢驗功效對于誤差項分布以及空間自相關程度的變化具有一定的穩健性.然而，相對于相互獨立的解釋變量所得到的結果，共線性在一定程度上會減弱檢驗的功效.這主要是由于自變量間的共線性的增強會導致各個自變量的系數不太容易識別，降低了檢驗功效.但是，這個不利的影響會隨著n或者c的增加而逐漸改善.

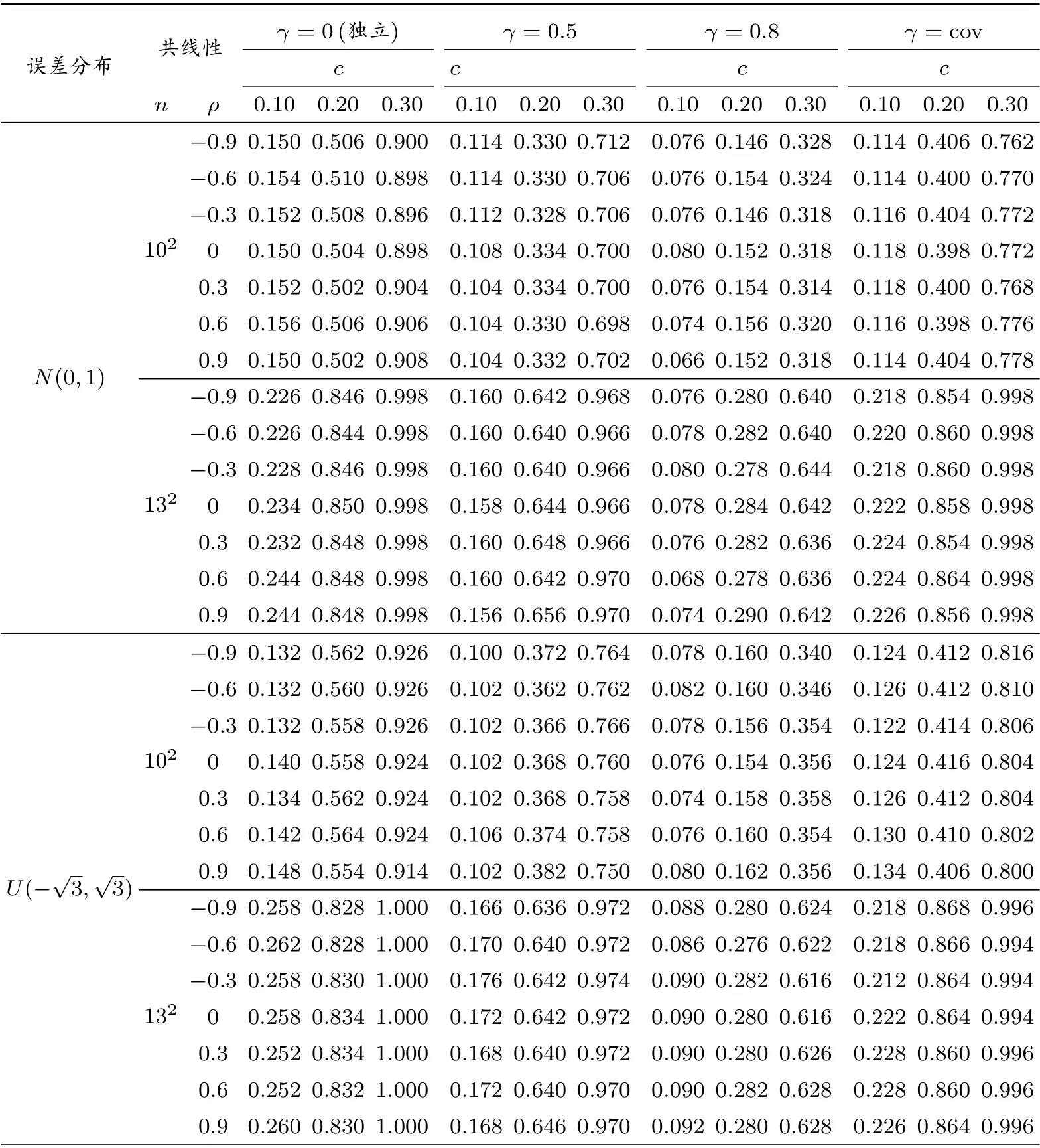
表2 當α=0.05時的檢驗功效

續表2 當α=0.05時的檢驗功效

5 小結

通過基于殘差的Bootstrap方法來逼近檢驗統計量的零分布，本文建立了確定變系數空間自回歸模型中的常系數項的檢驗方法.通過模擬試驗驗證了這種方法的準確性和可靠性.同時，本文還分別給出了在不同的誤差分布、空間相關性參數以及解釋變量的共線性程度這些情形下的模擬結果，進一步反映出該檢驗方法的穩健性.

對比變系數模型，半變系數模型反映了回歸函數的更為精細的結構，從而為分析和了解自變量對因變量的影響提供了更詳細的信息.但從實際應用角度來看，分析者事先往往并不知道哪些系數是常數，哪些是隨u而變化的.對于給定的數據集，我們可利用本文所給出的檢驗部分系數為常數的檢驗方法來識別變系數空間自回歸模型中的常值系數，從而為建立半變系數空間自回歸模型提供依據.