人類行為在戒煙動力學模型中的影響

李志民, 高建忠, 張太雷, 方 舒, 宋學力

(長安大學理學院，西安 710064)

1 Introduction

Smoking is called“the fifth threat”by the World Health Organization(WHO)[1,2].Epidemiological investigation showed that smoking is one of the important pathogenic factors oflung cancer[3].Many scholars have done a lot of work on quitting smoking models[4-11].In[11],Zebet alstudied a new quitting smoking model with squareroot of potential and occasional smokers of model.The local and global stability of the model and its general solution are discussed.Nowadays,due to the rapid development of science and technology information technology,we can understand the detailsof disease outbreaks through the Internet,newspapers,television,radio stations and government announcements.As a result,these media reports and health education will greatly affect human behavior,which can lead to a significant reduction in outbreak morbidity and mortality.In[12],Wanget alstudied the impact of human behavior on cholera infection by the basic reproduction number.However,no one considers the impact of human behavior in the quitting smoking model.In this paper,based on the previous articles[10–12],a goal is to improve our quantitative understanding of the impact of human behavior on disease dynamics.In particular,we will incorporate human behavior into the mathematical model of quitting smoking.

2 M odel description

In order to describe the model,P(t),L(t),S(t)andQ(t)represent the number of potential smokers,occasional smokers,smokersand quit smokersat timet,respectively.The total population number at timetis expressed byN(t)=P(t)+L(t)+S(t)+Q(t).Main assumptions are as follows:(i)λis constant birth rate for the potential smokers;(ii)μis the natural death rate anddrepresents death rate for potential smokers,occasional smokers and quit smokers related to smoking disease.d+αrepresents death rate for smokers(high mortality due to heavy smoking).γis the conversion rate from occasional smokers to smokers.δis the rate of quitting smoking.By the above assumptions(i)–(ii),we can formulate aPLSQquitting smoking model as follows

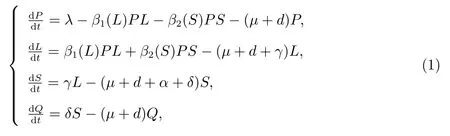
hereρdenote the spectral radius.The transmission of smoking behavior is similar to the disease,soT(type reproduction number[12])can be used to describe the dynamic behavior of smokers.From[15,16],we have the type reproduction numberT1can be easily defined in terms of the elementsmij:T1exists providedm22<1.In view ofm21=m22=0,by(2),the type reproduction number associated with the infectious humans is given by

It has been shown in[15]thatR0<1(=1,>1)?T1<1(=1,>1).

3 Equilibrium analysis

By direct calculation,we find that model(1)always has a non-smoker equilibriumE0and its smoker equilibriumE?satisfies the following equation

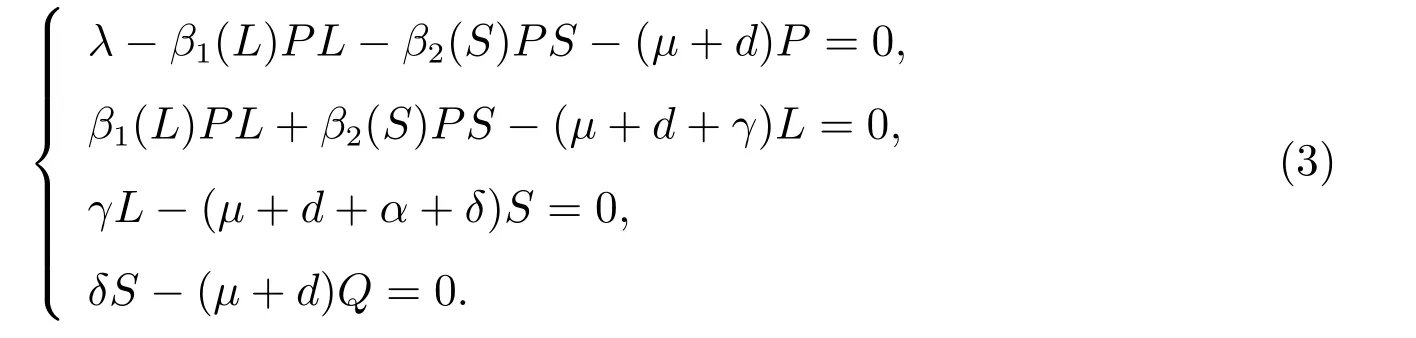
After sorting out,we have

Noting(4),the first and fourth equations are

we see that:

Theorem 1 IfR0≤1,then system(1)has a unique equilibriumE0.E0is locally asymptotically stable whenR0<1 and Lyapunov stable whenR0=1.

Proof We consider an equivalent system of model(1)

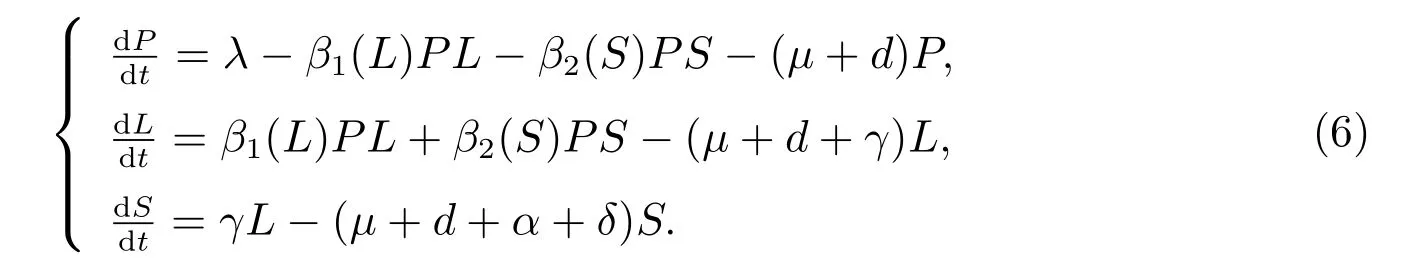
The Jacobian matrix of the vector field described by system(6)is

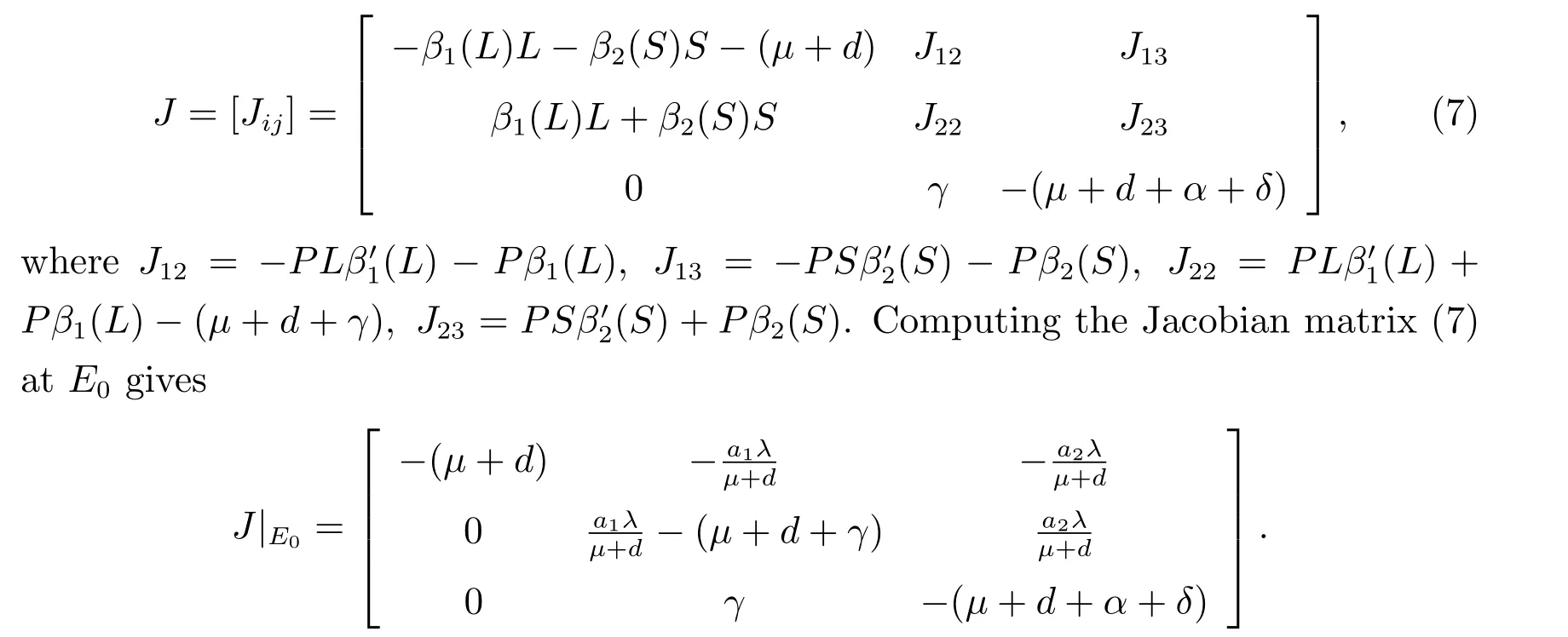
According to the relation between root and coefficient,we get

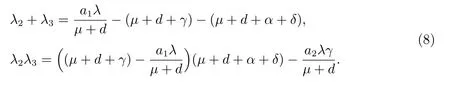
SinceR0≤1,we can obtainλ2+λ3<0,λ2λ3≥0,that is,λ2andλ3have both negative real part.So,all of the eigenvalues of the characteristic equation are negative real part.Hence,the equilibriumE0is locally asymptotically stable in the interior of Ω.This completes the proof of Theorem 1.

Theorem 2 IfR0>1,then system(1)has two equilibriaE0andE?.E0is unstable andE?is locally asymptotically stable asR0>1.

Proof We know thatE0is unstable whenR0>1 from(8).Now,we will prove that theE?is locally asymptotically stable.Evaluating the Jacobian matrix(7)at theE?,we find the characteristic equation ofJ|E?is given byλ3+c1λ2+c2λ+c3=0,where

c1=?(J11+J22+J33)|E?,

c2=(?J12J21+J11J22+J22J33+J11J33?J13J31?J23J32)|E?,

c3=(?J22J11J33+J22J13J31+J12J21J33+J11J23J32?J12J23J31?J13J21J32)|E?.

Ifc1>0,c2>0,c3>0 andc1c2?c3>0 holds,according to the Routh-Hurwitz criterion,we know thatE?is locally asymptotically stable.In fact

J11=?β1(L)L?β2(S)S?(μ+d)<0,

J22=PLβ′1(L)+Pβ1(L)?(μ+d+γ)=P(Lβ1(L))′?(μ+d+γ)<0,

J33=?(μ+d+α+δ)<0,

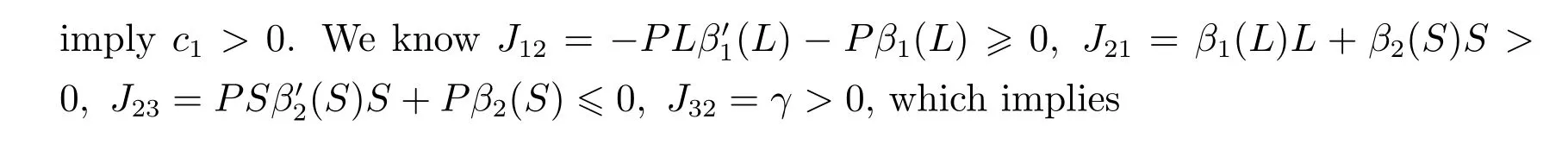
c2=β1(L)L(μ+d+γ)+β2(S)S(μ+d+γ)+(μ+d)(μ+d+γ)?P(μ+d)(Lβ1(L))′+J22J33+J11J33?J13J31?J23J32>0,

c3=(β1(L)L+β2(S)S)(μ+d+γ)(μ+d+α+δ)+(μ+d)(μ+d+γ)(μ+d+α+δ)?(μ+d)P(Lβ1(L))′(μ+d+α+δ)?P(Sβ2(S))′(μ+d),

by the condition(xβi(x))′≤0(i=1,2),we getc3>0.Thus

By simplecalculation,wehaveJ23=?J13,J22=?J12?(μ+d+γ),J11=?J21?(μ+d).Further we can obtain

Substituting(10)into(9),we obtain

Theorem 3 IfR0≤1,E0is globally asymptotically stable in the regionΩ.

Proof Let

4 Numerical simulation

In this section,some numerical results of system(1)are presented for supporting the analytic results obtained above.Here all the parameters values are estimated.The model parameters are taken as:

1)λ=0.5,a1=0.6,a2=0.7,b1=0.04,b2=0.04,μ=0.35,d=0.2,γ=0.2,δ=0.1,α=0.15,thenR0=0.9394.By Theorem 3,we get the number of people who smoke tends to zero.Here we choose initial valueP(0)=0.5,L(0)=0.6,S(0)=0.7,Q(0)=0.4,see Figure 1;

2)λ=0.5,a1=0.6,a2=0.7,b1=0.04,b2=0.04,μ=0.1,d=0.2,γ=0.2,δ=0.1,α=0.15,thenR0=2.8485.By Theorem 4,we know the number of smokers will continue.Here we choose initial valueP(0)=0.5,L(0)=0.6,S(0)=0.7,Q(0)=0.4,see Figure 2;

Figure 1 The global stability of the model(1)

Figur e 2 The permanence of the model(1)

3) From Figure 3,it can be shown results for the partial rank correlation coeffi-cients(PRCCs)[19]and these results illustrate the dependence ofR0on each parameter.From thebiological significanceof the established model,weonly studied the sensitivity of contact rateβi(i=1,2),the rate of quitting smokingδ,the conversion rate from occasional smokers to smokersγ,death rate for smokersd+α(high mortality due to heavy smoking)onR0.

From Figure 4 to Figure 10,only the values of the parametersa1,a2,δ,γ,d+α,b1andb2are changed,and other parameters values are thesame as Figure 2.Therefore,in order to reduce and control the number of smokers,we can increase the rate of quitting smokingδand decrease contact rateai(i=1,2)by scientific means from the above analysis,see Figure 4 to Figure 6.

Figure 3 PRCCs for the aggregate R 0 and each input parameter variable

Figure 4 The influence of parameter a1 on the value of S(t)

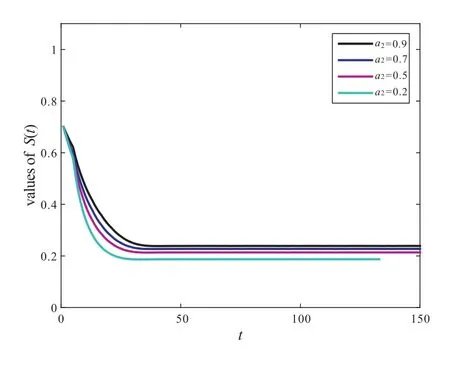
Figure 5 The influence of paramet a2 on the value of S(t)

er Figur e 6 The influence of parameter δon the value of S(t)

Figure 7 The influence of parameter γon the value of S(t)

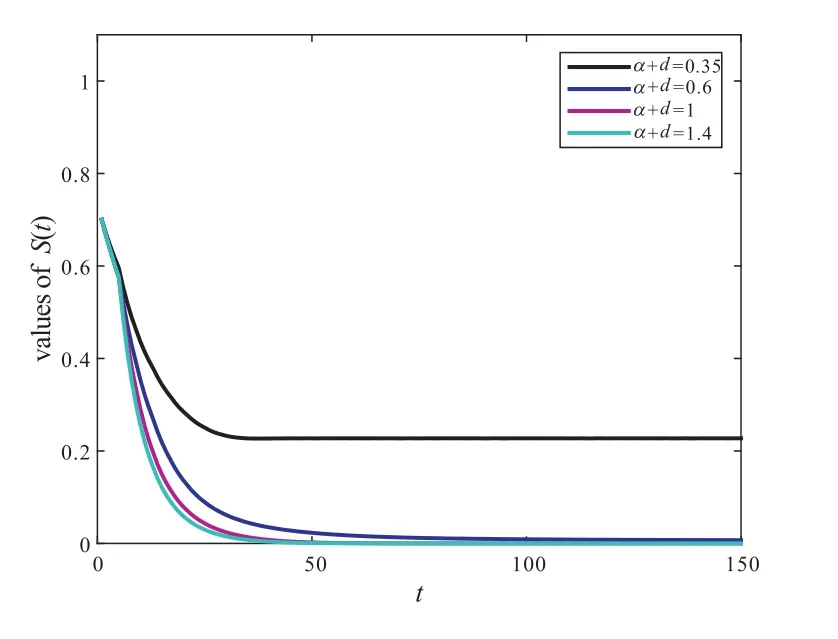
Figure 8 The influence of parameter α+d on the value of S(t)

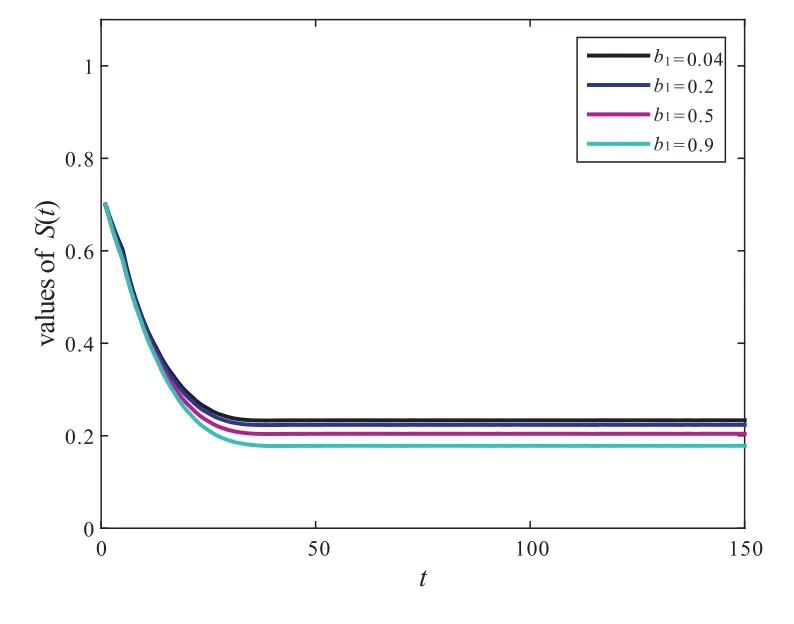
Figure 9 The influence of parameter b1 on the value of S(t)

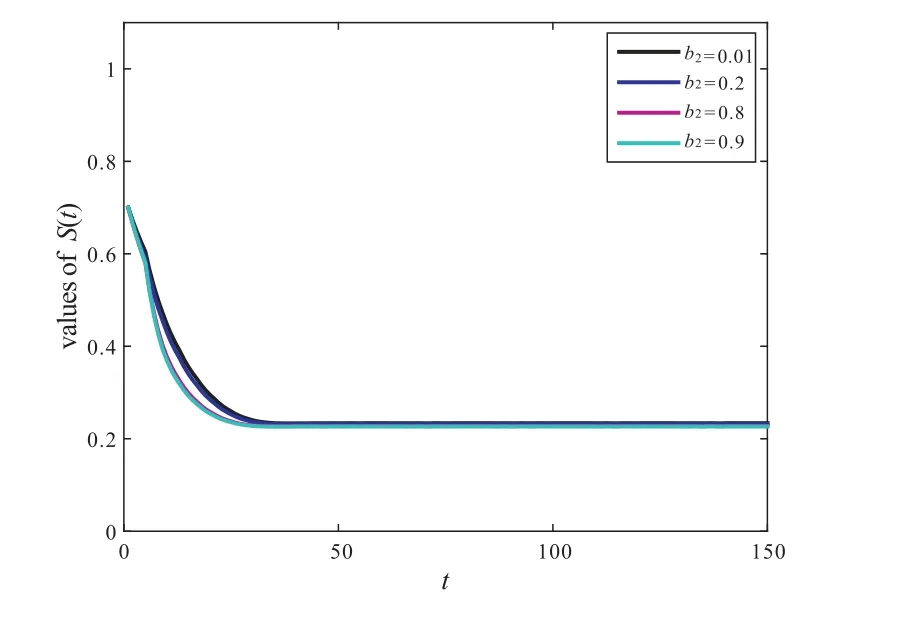
Figure 10 The influence of parameter b2 on the value of S(t)

Prop osition 1 IfR0>1,then theS?coordinate of the unique smoking equilibrium of model(1),S?is strictly decreasing with the increase ofbi(i=1,2)due to behavior change.

Proof SinceR0>1,there exists a unique smoking equilibrium(P?,L?,S?,Q?)of the system(1),by equations(5),we have

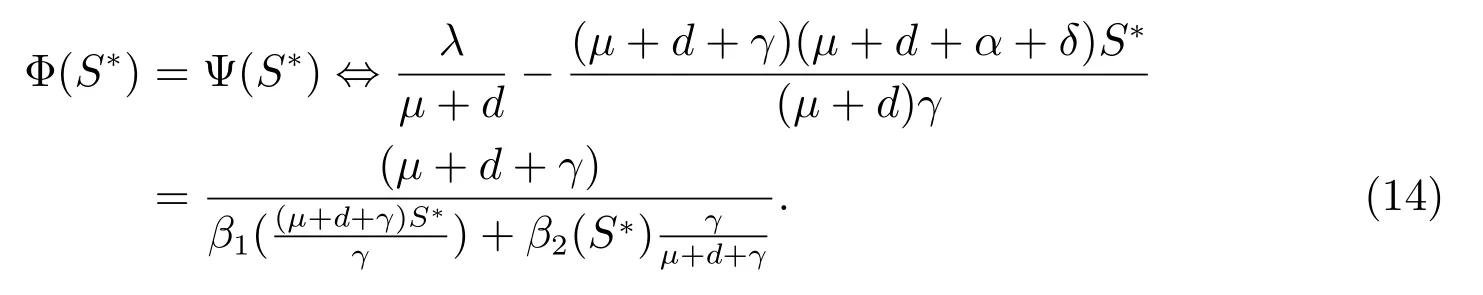
It follows(14)that

where

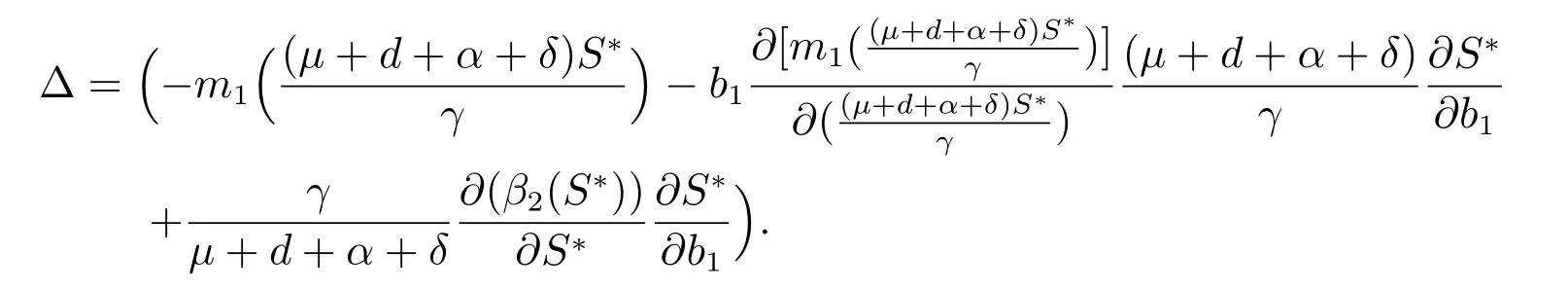
From the basic reproduction numberR0,we can see that there is no the value ofbi(i=1,2)in the expression ofR0and we do not know the effect ofbi(i=1,2)on the model.But as can be seen from Proposition 1,the value ofbi(i=1,2)is inversely proportional toS?,so we can reduce the value ofS?by increasingbi(i=1,2),see Figure9 and Figure10.A mathematically simplebut biologically important conclusion can be made from the above analysis on the smoker equilibriumE?.Namely,whenβi(i=1,2)is decreased as a result ofincorporating human behavior,the number of smokers is reduced as well.

5 Discussions

We propose a framework for modeling the effects of human behavior on smoking cessation dynamics.Our basic assumption is that therapid development ofinformation technology enables people to get the details of disease outbreaks through the Internet(especially popular social networking sites),newspapers,television,radio stations,as well as government announcements.Therefore,these media reports and health education will greatly affect human behavior,thereby significantly reducing the incidence of outbreaks and mortality.The same is true for smoking behavior,where people deliberately distance themselves from smokers.This paper is devoted to studying the effects of human behavior on quitting smoking dynamics.For ODE model,we have rigorously proved the basic reproduction numberR0,and analyzed the local and global stability of the model from the perspective of the basic reproduction number.In particular,whenR0≤1,the equilibriumE0of non-smokers is globally asymptotically stable,see Figure 1.WhenR0>1,the equilibriumE?of smokers is globally asymptotically stable,see Figure 2.Through thepartial rank correlation coefficients(PRCCs),the effects of different parameters on smokers’transmission were obtained,see Figure 3 to Figure 8.The effects of human behavior on smokers’transmission were deduced theoretically,see Proposition 1 and Figure 9 to Figure 10.Finally,the correctness of the theoretical derivation is verified by numerical simulation.Our results show that human behavior can reduce the number of smokers.