失電故障下海運冷藏集裝箱貨物升溫特性研究

闞安康 王彤洲 朱文兵 曹丹

摘要：為分析海運冷藏集裝箱制冷系統故障對貨物的影響，通過搭建實驗平臺和利用CFD仿真軟件對集裝箱內部溫度變化進行研究，重點分析堆放在不同位置的貨物的溫度變化。結果表明：靠近風口位置的貨物，因換熱強度大，溫度回升速度相對較快。

關鍵詞：

冷藏集裝箱; 失電故障; 冷藏貨物; 溫度變化

中圖分類號：? U664.87

文獻標志碼：? A

Study on temperature rise characteristics of marine

reefer container cargo under power-off fault

KAN Ankang， WANG Tongzhou， ZHU Wenbing， CAO Dan

（Merchant Marine College， Shanghai Maritime University， Shanghai 201306， China）

Abstract：

To analyze the influence of the fault of the marine reefer container refrigeration system on the cargo， the temperature change in the container is studied by setting up the experimental platform and using the CFD simulation software， and the temperature change of the cargo stacked in different positions is analyzed specifically. The results show that the temperature of the cargo near the air inlet and outlet rises relatively fast because of the high heat transfer intensity.

Key words：

reefer container; power-off fault; refrigerated cargo; temperature change

收稿日期： 2020-07-13

修回日期： 2020-08-19

基金項目： 上海市自然科學基金（15ZR1419900）

作者簡介：

闞安康（1981—），男，山東濟寧人，高級工程師，博士，研究方向為多孔介質傳熱傳質、低溫與制冷技術等，

（E-mail）ankang0537@126.com

0 引 言

隨著越來越多的國家加入“一帶一路”，我國的海外貿易總量呈現逐年上升的趨勢[1]。另外隨著生活消費質量的提高，人們對來自世界不同地域的生鮮食品、生物醫藥制品、植物花卉等商品的需求量不斷增長。在這種背景下，市場對海洋冷藏運輸的需求量也逐漸上升，僅在2015年全球的總成交量就突破了1億t，環比增長2.8%，預計2021年將達到1.3億t[2]。海洋冷藏運輸是遠洋貿易運輸的重要組成部分，相關企業對冷藏運輸設備的生產與投入使用量每年以近6%～15%的速度增長，全球海運冷藏集裝箱保有量已經超過200萬TEU[3]。

冷藏集裝箱是海運冷鏈中的重要設備，這種箱體可以提供相對穩定的低溫環境以降低貨物的變質速率。有關冷藏集裝箱的研究成果已經很多，比如：闞安康等[4]、張哲等[5]、KAYANSAYAN等[6]通過CFD仿真軟件研究了冷藏集裝箱內部的溫度場和空氣流場的變化規律;劉亞姣等[7]、樓海軍等[8]、DEFRAEYE等[9]研究了貨物的堆放方式對集裝箱內部溫度場的影響;BUDIYANTO等[10]研究了太陽輻射等外界環境因素對冷藏集裝箱的影響。

由于海洋氣候環境變化、外力碰撞等不確定因素的影響，冷藏集裝箱制冷系統可能出現故障，經過長時間的運輸后，箱內貨物的品質往往已經變差。為減少此類情況的發生，張珍[11]研究了冷藏集裝箱故障的智能診斷方法，為及時發現故障集裝箱提供了快速有效的措施;BADIA-MELIS等[12]研究了優化貨物溫濕度監測系統有效性的方法。

冷藏集裝箱最常見的故障是制冷系統失效，在涉及海洋冷藏運輸的國際貿易糾紛中有很多由此類故障導致的貨物受損案例。為了解制冷系統故障對貨物溫度的影響，本研究通過仿真分析與實驗測定相結合的方式，研究冷藏

集裝箱制冷系統失效后箱內空氣環境和貨物堆垛內部溫度場的變化規律。

1 仿真與實驗研究方法

1.1 幾何模型與數學模型

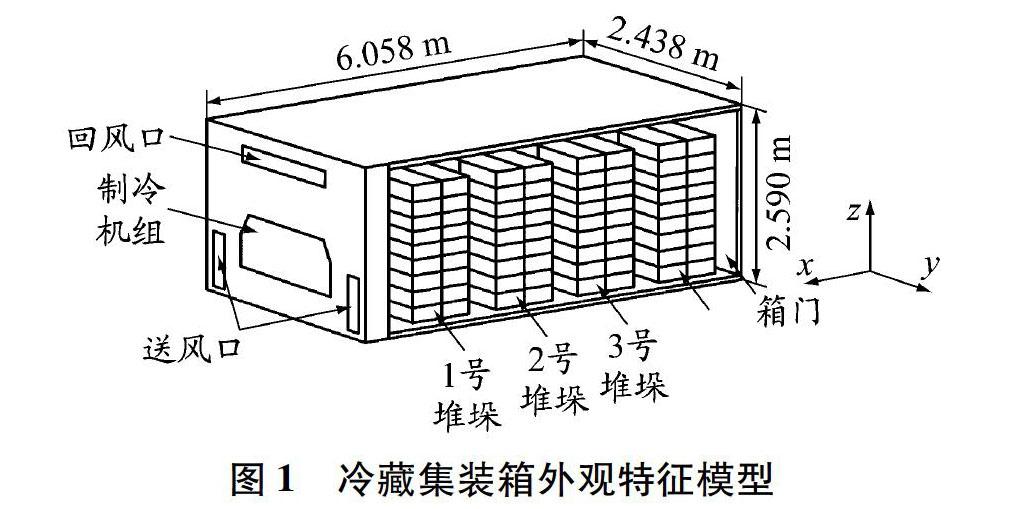
幾何模型是根據20英尺（1英尺=0.304 8 m）標準冷藏集裝箱的實際外形特征建立的，模型的外部尺寸為6.058 m×2.438 m×2.590 m（x、y、z方向，下同）;箱體壁厚0.1 m，其中內外金屬保護層厚度為0.02 m，隔熱夾層厚度為0.06 m;采用下送風上回風的方式，風口位置具體如圖1所示;模型內部放置有4個立方體堆垛結構，其尺寸均為1.08 m×2.16 m×1.62 m，相鄰堆垛之間的距離為0.35 m。

為簡化分析，假設：①壁面對流換熱系數為常數，不隨時間變化;

②堆垛為均質整體，所有材料的熱物性均為各向同性，且不隨時間和溫度變化;③堆垛內部無內熱源，并忽略輻射換熱和漏熱的影響;④空氣為不可壓縮流體，滿足Boussinesq條件，并且密度變化僅對浮升力具有影響;⑤忽略箱體中復雜結構（如T型槽）和貨物包裝材料的影響。

在集裝箱壁面和貨物內部存在熱傳導，而在表面存在對流換熱，其控制方程為

Tt=a2Tx2+

2Ty2+2Tz2

（1）

-λ·T=h（T-Tair）（2）

式中：a為熱擴散系數，m2/s;T為集裝箱內某點的溫度，Tair為空氣溫度，K;

t為時間，s;λ為材料的導熱

系數，W/（m·K）;h為對流換熱系數，W/（m2·K）。

Navier-Stokes（N-S）方程是流體力學中的重要理論方程，可以用于揭示流體的流場和傳熱規律。對于不可壓縮流體，其主要控制方程如下：

ρt+·（ρv）=0

（3）

（ρvi）t+（ρvivj）xj=

-pxi+·（μ·vj）+Si

（4）

（ρT）t+·（ρvT）=·Kcp·T+ST

（5）

v=（vx，vy，vz）

（6）

式中：ρ為流體密度，kg/m3;v為流體速度矢量;

vx、vy、vz分別為流體在x、y、z方向上的速度分量;

μ為流體的黏性因數;p為流體對應位置處的壓力，Pa;K為流體導熱系數，W/（m·K）;cp為流體的定壓熱容，J/（kg·K）;Si和ST為流體的源項。式（3）～（5）分別為質量守恒方程、動量守恒方程和能量守恒方程。

k-ε模型在工程上常用于湍流條件下換熱的計算。該計算方法重點考慮流體的湍動能k和湍動能耗散率ε兩項參數。對于沒有源項且不可壓縮的流體，其控制方程[13]如下：

（ρk）t+（ρkvi）xi=xj

μ+μtσkkxj+Gk-ρ

（7）

（ρε）t+（ρεvi）xi=xj

μ+μtσεεxj+

C1εεkGk-C2ερε2k

（8）

其中k與ε常采用下式進行近似計算：

k=3（vI）2/2

（9）

ε=C3/4μk3/2/l

（10）

式（7）～（10）中：Gk為由速度梯度產生的動能;C1ε、C2ε和Cμ為經驗常數，一般可取C1ε=1.44，C2ε=1.92，Cμ=0.09;σk和σε分別為湍動能和湍動能耗散率對應的普朗特數，可取σk=1.0，σε=1.3;I和l分別為湍流強度和湍流尺度。將上式與N-S方程進行耦合，就可以計算出流體各參數在任意時間、任意位置的值。

1.2 仿真模型與邊界條件

為進一步分析，利用ANSYS-CFD軟件建立相應的網格模型，并借助Fluent軟件進行模擬計算。首先用網格劃分軟件對幾何模型進行網格劃分。為提高計算速度和精度，采用四面體與六面體混合型網格劃分方法，其中堆垛計算域采用六面體網格，空氣域采用四面體網格，靠近風口和各交界壁面的計算域網格被局部加密。最終得到的網格模型的網格總數為251 681，節點數為72 428。借助Fluent 18.0進行求解計算，選擇壓力模型、k-ε標準方程和能量方程，采用二階迎風離散格式和SIMPLE壓力修正算法。這種算法計算時先假定上述方程中的初始速度和壓力，通過求解動量方程獲得壓力修正值，再根據新的壓力值修正速度項，并相應得出溫度以及其他參數的值。

貨物和箱體壁面材料的熱物性參數按表1選取。在邊界條件設置中，送風口選擇velocity-inlet邊界條件，送風速度設為2 m/s。循環風機正常運行，考慮到做功和摩擦等因素，其部分機械能會轉化為熱能進入箱內，因此將循環風機近似視為穩定的送風熱源。根據文獻[14]，

將循環風機視為功率密度為50 W/m3的穩定體熱源，熱量通過送風口進入箱內。回風口的風速和壓力未知，假定空氣流動可以充分發展，此時回風口選擇outflow條件。集裝箱壁面的對流換熱系數設為18.3 W/（m2·K），初始溫度設為255 K，外部空氣溫度設為313 K。在計算過程中，設時間步長為1 s，總共計算86 400步。

1.3 實驗模型

為獲得盡可能接近真實情況的溫度變化數據，并驗證仿真計算結果，選擇上海海事大學實驗用20英尺標準冷藏集裝箱作為實驗平臺。箱體內部4個堆垛按照幾何模型分布于集裝箱的不同位置。采用單位尺寸為0.54 m×0.36 m×

0.18 m的箱體裝載冷凍加工食品（其熱物性見表1）;每個堆垛按雙排6列9層方式緊密疊放貨物（見圖2a）;采用熱電偶監測各個堆垛不同位置處的溫度變化，所使用的熱電偶為T型，其誤差范圍為[-0.1，0.1] K，數據采集器為安捷倫34972A;溫度監測點的分布見圖2b，數據采集間隔設置為10 s。

實驗模擬的是在集裝箱制冷系統突發局部失電故障，導致送風溫度無法達到預定值的情況下，集裝箱內部的溫度變化。實驗開始前，集裝箱內部溫度為-18 ℃（255 K）且貨物已經進行了充分的冷凍，整個實驗過程持續24 h。

2 結果與討論

2.1 仿真計算結果

圖3展示了與實驗中溫度監測點相對應的網格節點的溫度仿真計算結果?？紤]到對稱性，這里給出的是每組對稱監測點的平均溫度。通過觀察可以發現，在集裝箱失電24 h后，1、2、3、4號堆垛模型中監測點A處溫度上升幅度分別為8.8、7.3、6.7和5.6 K，監測點B處溫度上升幅度分別為6.1、5.3、4.8和4.5 K，監測點C處溫度上升幅度分別為3.6、2.2、1.9和1.8 K。通過對比可以發現，越靠近風口的堆垛溫度變化越快，位置越高的監測點溫度變化越快。另一方面，各堆垛在豎直方向上的最大溫差分別為5.2、5.1、4.8和3.8 K，這說明越靠近風口的堆垛溫度場分布越不均勻。

圖4展示了集裝箱失電3、6、12、24 h后各堆垛模型在同一時刻的溫度場分布情況。隨著時間的推移，堆垛表面溫度逐漸升高，可以明顯發現堆垛的4個頂角以及邊緣位置溫度變化最快;溫度擾動會逐漸向底部以及內部中心擴散。通過比較可知，1號堆垛熱擴散最快，2號和3號次之，4號相對最慢。不同堆垛熱擴散快慢不同的原因主要是不同堆垛表面所受到空氣流動擾動強度不同。圖5和6分別展示了集裝箱內部空氣流線的速度分布和溫度場分布。通過觀察可知，在靠近送風口和回風口的區域空氣射流速度大，擾動劇烈，甚至在射流兩側形成了局部旋渦，因而靠近此位置的堆垛表面的對流換熱也就相對更強，溫度變化更快。另一方面，由于相鄰堆垛之間的空間狹小，湍流現象也就更為明顯。然而，隨著流動距離的增加，空氣射流速度會有所降低，湍流強度也會逐漸降低。在距離風口較遠的4號堆垛和箱門附近的空氣湍流強度已經明顯衰減，對流換熱強度也就相應最小。另外，因為空氣與貨物之間的換熱，空氣射流溫度隨著流動距離的增加而降低。在以上因素的共同影響下，4號堆垛的溫度上升相對慢一些。

2.2 實驗驗證結果

各監測點的溫度隨時間變化的實驗結果見圖7。通過觀察可以發現：隨著時間的推移，各堆垛的溫度都會逐漸上升;位于堆垛最上方的監測點A溫度上升幅度最大，位于堆垛最下方的監測點C溫度上升幅度最小;在相同的監測位置，靠近送風口的1號堆垛溫度上升最快，靠近箱門的4號堆垛溫度上升最慢。

具體地，在集裝箱失電24 h后，1、2、3、4號堆垛的監測點A溫度上升幅度分別為8.7、7.2、6.6、5.4 K，監測點B的溫度上升幅度分別為6.3、5.5、5.1、4.8 K，監測點C的溫度上升幅度分別為3.3、2.5、2.4、2.1 K。實驗結果與模擬結果相似，即越靠近風口的堆垛溫度上升越快，且位置越高的貨物溫度變化越快，其原因是對流換熱越強，冷量耗散速度就越快。由于貨物本身具有較強的蓄冷能力，熱擴散速度較小，加之底部空氣擾動較弱，所以位置較低的貨物溫度變化較慢。另一方面，在集裝箱失電24 h后，1、2、3、4號堆垛在垂直地面方向上的溫差分別為5.4、4.7、4.2、3.3 K。1號堆垛的溫度梯度最大，4號堆垛的溫度梯度最小，這同樣說明越靠近風口的堆垛溫度變化越不均勻。

2.3 誤差分析

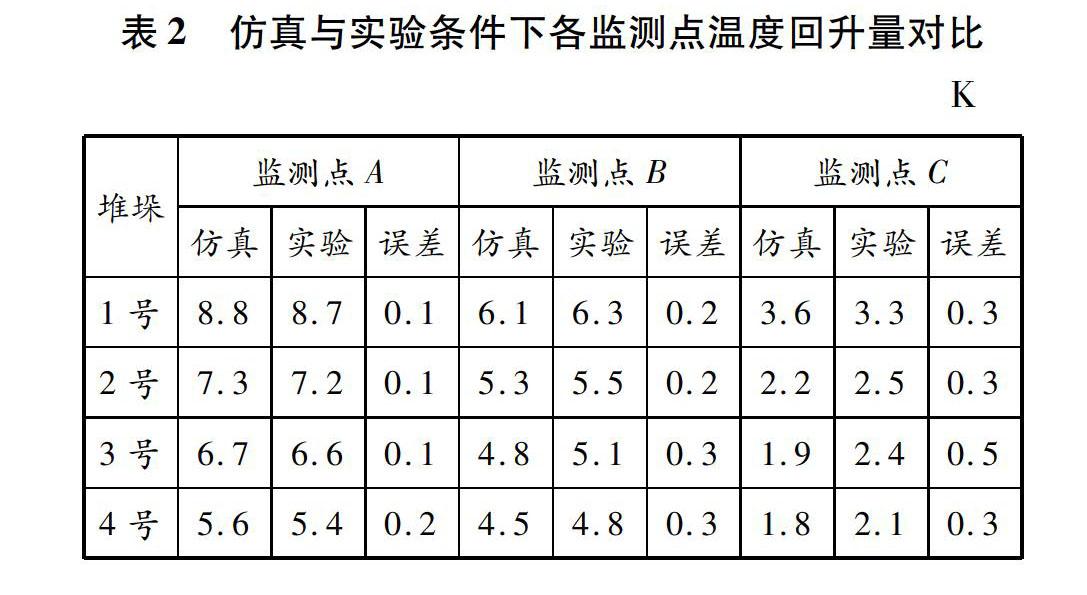
在集裝箱失電24 h后，各監測點溫度回升量的仿真結果和實驗結果見表2。誤差主要是由實驗中一些不可控因素造成的：貨物箱體之間無法完全緊密貼合，存在一定的接觸熱阻，且少量的空氣可通過縫隙滲入堆垛內部進而影響熱量的擴散過程;各貨物箱體內部填充材料的密度可能存在少許差異，貨物箱體外表面附著少量的冰。從整體來看，實驗結果與仿真結果吻合較好，誤差基本控制在0.3 K以內，這說明建立的模型是合理的。

3 結 論

研究冷藏集裝箱在制冷系統失效條件下內部貨物溫度隨時間變化的情況。利用CFD軟件分析了貨物的溫度變化規律及其形成原因，并通過搭建相應的實驗模型來驗證仿真結果。主要結論如下：

（1）在靠近風口的位置，由于風速大、對流換熱強，堆垛整體溫度上升快，且溫度變化不均勻;碼放于堆垛頂角和邊緣的貨物溫度變化快于其他位置。

（2）相鄰堆垛之間的湍流現象導致換熱加強，但隨著空氣流動距離的增加，氣流湍動強度和溫度會衰減，則距離風口越遠的堆垛溫度變化也就相對越慢。

在船舶實際航行中，從發現故障集裝箱到采取措施需要一定的時間。為盡可能延長集裝箱內部低溫環境持續時間，可以在堆垛邊緣位置的貨物箱體內放入蓄冷劑，或者將質量大、蓄冷能力強的貨物碼放于堆垛的外表面，從而減小貨物溫度上升速率。

參考文獻：

[1]王慧珍. “一帶一路”背景下冷鏈物流對農產品進出口的影響[J]. 物流科技， 2020， 43（5）： 151-152. DOI： 10.13714/j.cnki.1002-3100.2020.05.038.

[2]CASTELEIN B， GEERLINGS H， DUIN R V. The reefer container market and academic research： a review study[J]. Journal of Cleaner Production， 2020， 256： 120654. DOI： 10.1016/j.jclepro.2020.120654.

[3]郭志鵬， 闞安康， 孟闖， 等. 冷藏集裝箱內溫度場的數值模擬與實驗[J]. 上海海事大學學報， 2017， 38（2）： 82-87. DOI： 10.13340/j.jsmu.2017.02.016.

[4]闞安康， 王寧， 毛賞， 等. 船舶冷藏集裝箱艙室內通風方式的數值模擬及實驗研究[J]. 上海海事大學學報， 2019， 40（2）： 88-94. DOI： 10.13340/j.jsmu.2019.02.016.

[5]張哲， 郝俊杰， 李曼， 等. 冷藏集裝箱內部溫度場的理論與實驗研究[J]. 低溫與超導， 2016， 44（6）： 76-80. DOI： 10.16711/j.1001-7100.2016.06.016.

[6]KAYANSAYAN N， ALPTEKIN E， EZAN M A. Thermal analysis of airflow inside a refrigerated container[J]. International Journal of Refrigeration， 2017， 84： 76-91. DOI： 10.1016/j.ijrefrig.2017.08.008.

[7]劉亞姣， 楊小鳳， 莊春龍， 等. 果蔬堆碼方式對機械式冷藏集裝箱內溫度場的影響[J]. 后勤工程學院學報， 2015， 31（6）： 67-72. DOI： 10.3969/j.issn.1672-7843.2015.06.012.

[8]樓海軍， 闞安康. 貨物堆碼方式對海運冷藏集裝箱內溫度場分布的影響[J]. 上海海事大學學報， 2014， 35（4）： 55-58. DOI： 10.13340/j.jsmu.2014.04.011.

[9]DEFRAEYE T， VERBOUEN P， OPARA U L， et al. Feasibility of ambient loading of citrus fruit into refrigerated containers for cooling during marine transport[J]. Biosystems Engineering， 2015， 134： 20-30. DOI： 10.1016/j.biosystemseng.2015.03.012.

[10]BUDIYANTO M A， SHINODA T. The effect of solar radiation on the energy consumption of refrigerated container[J]. Case Studies in Thermal Engineering， 2018， 12： 687-695. DOI： 10.1016/j.csite.2018.09.005.

[11]張珍. 冷藏集裝箱遠程故障診斷系統研究[D]. 上海： 上海海事大學， 2006.

[12]BADIA-MELIS R， CARTHY U M， UYSAL I. Data estimation methods for predicting temperatures of fruit in refrigerated containers[J]. Biosystems Engineering， 2016， 151： 261-272. DOI： 10.1016/j.biosystemseng.2016.09.009.

[13]高超. 海運冷藏集裝箱內部溫度場研究[D]. 大連： 大連海事大學， 2018.

[14]薛威. 船用冷藏集裝箱制冷機組的設計與特性研究[D]. 廈門： 集美大學， 2013.

[15]TSANG A H F， YUNG W K. Development of an adaptive food preservation system for food quality and energy efficiency enhancement[J]. International Journal of Refrigeration， 2017， 76： 342-355. DOI： 10.1016/j.ijrefrig.2017.02.006.

（編輯 賈裙平）