基于信息增強的多視角矩陣分類器設計

朱昌明 高玉森

摘要：由于受限于人工成本，很多現實世界中的多視角數據集是由少量有標簽樣本和大量無標檢樣本組成的。當前傳統的多視角矩陣分類器無法有效處理這類數據集。為了處理這個問題，將Universum學習引入多視角矩陣分類器中，提出基于信息增強的多視角矩陣分類器。由于Universum學習可以生成額外的無標簽樣本，這類樣本雖然沒有被指定類別標簽，但是包含了部分有標簽樣本的信息，所以Universum學習可以增強有效樣本信息。實驗表明，相比于傳統的多視角矩陣分類器，本文提出的基于信息增強的多視角矩陣分類器具有更好的分類性能。

關鍵詞：

Universum學習; 多視角; 矩陣分類器

中圖分類號：? TP391.4

文獻標志碼：? A

Information enhancement-based multi-view matrix classifier design

ZHU Changming， GAO Yusen

（Information Engineering College， Shanghai Maritime University， Shanghai 201306， China）

Abstract：

Due to the limitation of labor cost， many real-world multi-view datasets are composed of a small number of labeled samples and a large number of unlabeled samples. At present， the traditional multi-view matrix classifier cannot deal with this kind of datasets effectively. In order to deal with this problem， Universum learning is introduced into the multi-view matrix classifier， and an information enhancement-based multi-view matrix classifier is proposed. Because Universum learning can generate additional unlabeled samples that contain some information of labeled samples， Universum learning can enhance the effective sample information. Experimental results show that， the proposed information enhancement-based multi-view matrix classifier is of better classification performance than the traditional multi-view matrix classifiers.

Key words：

Universum learning; multi-view; matrix classifier

收稿日期： 2020-05-10

修回日期： 2020-06-23

基金項目： 中國博士后基金（2019M651576）;上海市晨光計劃（18CG54）

作者簡介：

朱昌明（1988—），男，上海人，副教授，博士，研究方向為多視角學習、模式識別，（E-mail）cmzhu@shmtu.edu.cn

0 引 言

多視角數據集普遍存在于圖像處理、視頻追蹤、網頁分類等領域。數據集多由矩陣型樣本組成，因此通常采用多視角矩陣分類器（如改進的基于Nystrm的多核修正型Ho-Kashyap算法[1]（INMKMHKS）、雙重局部化多矩陣學習機[2]（DFLMMLM）、具有5方面樣本信息的多矩陣學習機[3]（MMLMFAPI）等）處理。隨著國際貿易發展、生活節奏變快，越來越多的樣本呈現出大批量產生的特征，但受限于人力成本，僅有一小部分樣本獲得了標記。換句話說，當前的大多數多視角數據集是由少量有標簽樣本和大量無標簽樣本構成的。這類數據集稱為半監督多視角數據集。傳統的多視角矩陣分類器無法有效處理這類數據集。

增強有效的樣本信息是處理這個問題的一種方式。眾所周知，有標簽樣本可以提供有利于分類器設計的有效樣本信息，而無標簽樣本能提供的這類有效的樣本信息很少。若可以以有標簽樣本為基礎生成一些樣本，則這類樣本可以提供有效的樣本信息，從而增強有利于分類器設計的樣本信息，并進一步提升分類器的性能。目前，Universum學習就是這樣的一種解決方式[4]。Universum學習通過生成包含有利于分類器設計的先驗知識和信息的額外無標簽樣本（即Universum樣本），并選擇其中的一部分加入原始數據集，來增強有效樣本信息并指導分類器設計。比如，對于有0、1、2、3、4、5、6、7、8、9總共10個數字的1 000多張圖片，要分類5和8，既可以用0、1、2、3、4、6、7、9這8個數字的圖片作為Universum樣本，也可以利用這些圖片來擬合生成一些包含了關于5和8的先驗知識的新圖片（這些新圖片雖然不能被歸為任務一類，但是它們在生成時涉及了5和8的相關信息，因此這些圖片也可以被認為是Universum樣本）。

經典的Universum樣本生成及選擇方法在CHEN等[5]和ZHU[6]的工作中有所涉及，即通過選取任意兩個不同類的有標簽多視角樣本，平均化它們的特征信息，從而構建一個新的無標簽樣本。新的無標簽樣本由于是通過有標簽樣本生成的，所以包含一定的先驗知識和信息。朱昌明等[7]把該樣本生成算法用于結構風險最小化問題中以驗證其在理論上的有效性。劉鴻等[8]將Universum樣本生成算法用于度量學習，以更真實地刻畫樣本之間的距離，提高分類和聚類的精度。此外，相關學者更從降維、模糊學習等角度驗證了Universum學習的兩大優點：①充分利用整個數據分布的域知識;②可獲取更多的有效樣本信息。[9-10]這些有效樣本信息對于指導分類器的構建有著重要的作用，可以提升分類器的性能。

為克服傳統多視角矩陣分類器的不足，本文以傳統的矩陣分類器（即基于矩陣樣本的修正型Ho-Kashyap算法（MatMHKS））[11]為基礎，引入Universum學習，并拓展到多視角領域，提出一個基于信息增強的多視角矩陣分類器（information enhancement-based multi-view MatMHKS， IMMatMHKS）。

1 IMMatMHKS

IMMatMHKS設計方法包含兩個步驟：第一步，通過Universum學習生成更多有用的Universum樣本;第二步，把這些模式用到多視角MatMHKS中，構建一個基于信息增強的多視角矩陣分類器設計方法，即IMMatMHKS。為此，本節由兩部分組成：第一部分描述Universum學習和生成Universum樣本，第二部分給出IMMatMHKS的訓練和優化步驟。

1.1 CIBU算法

為生成合適的Universum樣本，并增強有效的樣本信息，本文使用CIBU（creating in-between Universum）算法。

假設有一個多視角矩陣集Tmat={（A1，φ1），（A2，φ2），…，（AN，φN）}，φp∈[0，c]是類標簽（p=1，2，…，N），其中N和c分別表示有標簽樣本的數量和類別的數量。φp=0表示相應的樣本沒有標記，即該樣本為無標簽樣本;φp≠0表示相應的樣本為有標簽樣本。

先根據所有樣本的信息建立近鄰矩陣G。矩陣G第i行第j列的元素Gij由式（1）計算：

Gij=Ai-Aj22，Ai∈Nk（Aj）或Aj∈Nk（Ai）

+∞，其他

（1）

式中：Nk（Aj）或Nk（Ai）是Ai或Aj的k個最近鄰樣本的集合，Ai和Aj是兩個不同的樣本。

隨后，分別針對兩個不同的樣本Ai和Aj（其中至少有一個是有標簽樣本），根據其Gij進行判斷。若Gij的值不為無窮大，則由Ai和Aj得到一個Universum樣本A*k，其計算方式如下：

A*k=（Ai+Aj）/2

（2）

最后，在生成的Universum樣本集中選擇最小的UAk個Gij所對應的Universum樣本參與后續分類器的訓練。之所以選擇最小的UAk個Gij所對應的Universum樣本，是因為Gij越小，Ai與Aj之間的相似度越高，生成的Universum樣本所具有的先驗知識和有效樣本信息越多。至此，CIBU算法就完成了。

1.2 IMMatMHKS訓練與優化

假設有一個包含N個多視角向量樣本的集合Tvec={（x1，φ1），（x2，φ2），…，（xN，φN）}，其中樣本xp∈Rd，φp∈[0，c]為相應的類標簽，p=1，2，…，N。Tvec可以通過參考文獻[11]中給出的矩陣化技術被矩陣化到相應的多視角矩陣集Tmat={（A1，φ1），（A2，φ2），…，（AN，φN）}中，其中Ap∈Rd，d=n1×n2，p=1，2，…，N。另外，T*vec={x*1，x*2，…，x*M}是生成并選擇的用于訓練的M個Universum樣本

的集合，其被矩陣化后的

形式是T*mat=（A*1，A*2，…，A*M）。IMMatMHKS的目標函數為

min J|J（u，，v0，bp，b*q）=

Np=1（φp（uTAp+v0）-1-bp）2/2+

C（uTS1u+TS2）/2+

DMq=1（（uTA*q+v0）-1-b*q）2/2

（3）

式中：u、分別為左、右權向量;v0為偏置;bp為樣本Ap的松弛量;b*q為樣本A*q的松弛量;C和D為正則化參數，其作用是調節模型復雜度與分類誤差之間的平衡。

為求解式（3），令：Y=（y1，y2，…，yN）T，yp=φp（uTAp，1）T，p=1，2，…，N;v=（T，v0）T;b=（b1，b2，…，bN）T;IN×1=（1，1，…，1）T;Y*=（y*1，y*2，…，y*M），y*q=（uTA*q，1）T，q=1，2，…，M;b*=（b*1，b*2，…，b*M）T;I*M×1=（1，1，…，1）T。IMMatMHKS的目標函數可重寫為

min J|J（u，v，bp，b*q）=

（Yv-I-b）T（Yv-I-b）/2+

C（uTS1u+vTS～2v）/2+

D（Y*v-I*-b*）T（Y*v-I*-b）/2

（4）

式中S～2=S2000。由式（3）或式（4）無法直接獲取參數u、v、b、b*的最優值，因此采用梯度下降法對式（4）進行迭代求解。

先由式（4）對u、v、b、b*求偏導數，再令所求得的偏導數為0，得到權向量u和以及偏置v0的迭代結果。設定迭代終止條件，當迭代終止時會得到最優的權向量u和以及偏置v0，即權向量un和n以及偏置v0n，隨后便可利用這些最優值對測試樣本進行分類。

2 實驗分析

2.1 實驗設置

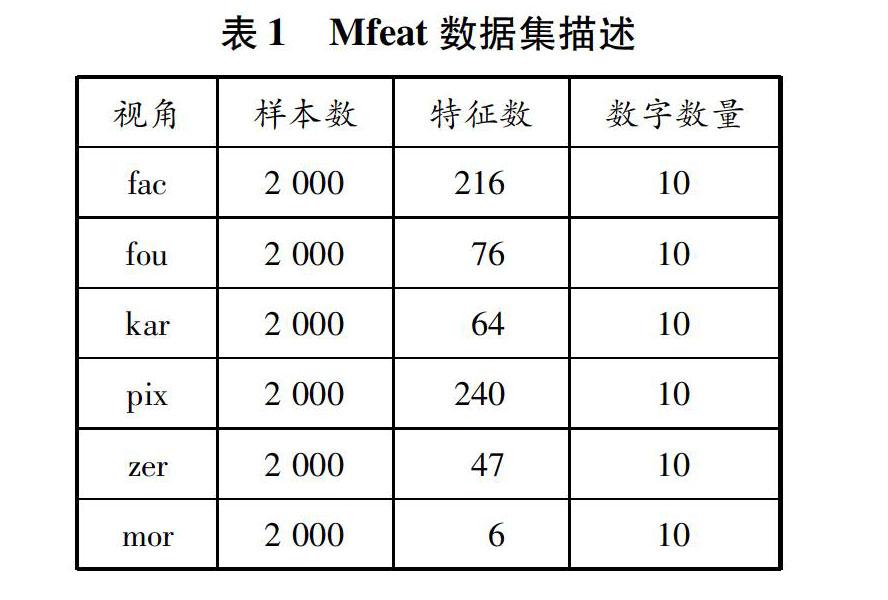
為驗證所提出的IMMatMHKS的有效性，選擇3個多視角數據集作為實驗數據，見表1～3。針對這些數據集，隨機選擇10%、20%、30%、40%、50%、60%的樣本作為訓練樣本，其余的樣本用于測試。另外，在訓練樣本中隨機選擇10%、20%、30%、40%、50%、60%、70%、80%、90%的樣本作為有標簽訓練樣本，其余的樣本作為無標簽訓練樣本。

選擇INMKMHKS、DFLMMLM和MMLMFAPI這3個傳統方法作為對比。這些方法的參數由相應的參考文獻可知。而對于本文提出的IMMatMHKS，其大部分參數設置可以參考文獻[11]。IMMatMHKS中的參數k和UAk設置如下：k=5;UAk為所有樣本數量的3倍。實際上，

k和UAk這兩個參數設置的不同，會影響IMMatMHKS的性能，但是通過大量實驗發現，由于Universum學習的引入，這兩個參數在大部分情況下都會使分類器的性能提高，因此本文中僅給出如上設置的實驗結果。

為獲得最佳參數，采用十重交叉驗證的方法：針對每組參數組合，將所使用的數據集的訓練樣本分為10份，每次取9份進行訓練，1份進行驗證，然后獲得一個分類性能;10次實驗之后，便得到一個平均結果;以平均結果最好的情況下的參數為最佳參數，對測試樣本進行測試實驗。

2.2 分類性能比較

為體現IMMatMHKS的有效性，采用準確率、真陽率、真陰率和F值（相應的指標概念可參考文獻[12]）等4個指標描述其性能。從表4可知：①就準確率、真陽率、真陰率來說，IMMatMHKS可以帶來相對較好的性能;②從F值的結果來看，IMMatMHKS的性能優勢并沒有明顯偏向正類和負類，具有普適性。總體而言，由于本文提出的IMMatMHKS引入了Universum學習，可以在識別同一個數據集時，通過信息的增強使更多的有效樣本信息參與分類器的訓練，所以IMMatMHKS比INMKMHKS、DFLMMLM、MMLMFAPI具有更好的分類性能。

2.3 時間性能比較

表5給出了在最佳參數的情況下，4種方法的訓練時間和測試時間。由表5可知，隨著Universum學習的引入，分類器的訓練需要更多的時間，但是由于增加的時間不超過10%，所以結合IMMatMHKS的性能優勢，這一現象是可以接受的。另外，從測試時間來看，在同一個數據集中，IMMatMHKS所需要的測試時間也不一定是最多的。當然，應當注意的是，對于一般的識別問題而言，時間上的差距可以通過硬件來彌補，而識別率上的差異則需要通過算法來彌補，因此IMMatMHKS在時間上的額外開銷并不會過多地影響其性能優勢。

2.4 顯著度分析

為驗證IMMatMHKS的優勢是顯著的，下面進行顯著度分析，即p值比較[13]。p值最早由FISHER提出，按照FISHER的理論，p值越小，兩種方法在同一個數據集上的差異越顯著。一般來說，當p>0.05時可以認為兩種方法在一個數據集上的差異是不顯著的，當p∈[0.01，0.05]時可以認為兩種方法在一個數據集上的差異是顯著的，而當p<0.01時可以認為兩種方法在一個數據集上的差異非常顯著。

為更好地表明IMMatMHKS的有效性，用表6表示在不同的評價指標下IMMatMHKS與參與對比的方法在不同數據集上的p值。

由表6可以明顯地看到，相對于其他對比方法，特別是INMKMHKS，本文提出的IMMatMHKS具有顯著的優勢。

2.5 訓練樣本和有標簽樣本比例的影響

由于在實驗中針對訓練樣本和有標簽樣本選擇了不同的比例，本文也給出樣本比例不同的情況下IMMatMHKS性能的變化。為簡化說明，本文只給出在不同的訓練樣本比例和有標簽訓練樣本比例的情況下

IMMatMHKS在Mfeat數據集上準確率的變化。盡管沒有給出IMMatMHKS在其他數據集和其他分類性能指標下的變化，但是這并不會影響結果。從表7可知，訓練樣本和有標簽訓練樣本的比例越高，IMMatMHKS在Mfeat數據集上的準確率越高，這也證明隨著信息的增強，有效樣本信息越多，可以更容易指導分類器的設計，從而提升分類器的性能。

3 總結與未來工作

在當前的模式識別領域中，多視角學習問題普遍存在。盡管已有學者提出一系列多視角矩陣分類器處理此類問題，但是受限于人工成本，現實世界中大多數多視角數據是由少量有標簽樣本和大量無標簽樣本組成的，傳統的多視角矩陣分類器對于此類問題的處理存在一定的困難。

本文在矩陣分類器中引入Universum學習，通過CIBU算法增強有效的樣本信息，并提出一個基于信息增強的多視角矩陣分類器（IMMatMHKS）。通過在Mfeat、Reuters、Corel等3個典型的多視角數據集上的實驗，驗證IMMatMHKS具有更高的分類性能且性能優勢顯著，只是訓練時間略有增加。本文的工作也驗證了隨著訓練樣本或有標簽訓練樣本比例的增加，矩陣分類器的性能也會增強。

除Universum學習外，還有很多其他的方法可以生成額外的樣本，如對抗網絡。由于本文的研究目的是驗證信息增強后分類器性能會提高，而Universum學習的時間開銷比對抗網絡的小，所以本文研究采用了Universum學習。未來工作會采用對抗網絡等方式加以深入研究，以更好地增強樣本信息。

參考文獻：

[1]ZHU Changming， GAO Daqi. Improved multi-kernel classification machine with Nystrm approximation technique[J]. Pattern Recognition， 2015， 48（4）： 1490-1509. DOI： 10.1016 / j.patcog.2014.10.029.

[2]ZHU Changming， WANG Zhe， GAO Daqi， et al. Double-fold localized multiple matrixized learning machine[J]. Information Sciences， 2015， 295： 196-220. DOI： 10.1016/j.ins.2014.10.024.

[3]ZHU Changming， GAO Daqi. Multiple matrix learning machine with five aspects of pattern information[J]. Knowledge-Based Systems， 2015，? 83： 13-31. DOI： 10.1016/j.knosys.2015.03.004.

[4]WESTON J， COLLOBERT R， SINZ F， et al. Inference with the Universum[C]//Proceedings of the 23rd International Conference on Machine Learning. ICML， 2006： 1009-1016. DOI： 10.1145/1143844.1143971.

[5]CHEN Xiaohong， YIN Hujun， JIANG Fan， et al. Multi-view dimensionality reduction based on Universum learning[J]. Neurocomputing， 2018， 275： 2279-2286. DOI： 10.1016/j.neucom.2017.11.006.

[6]ZHU Changming. Improved multi-kernel classification machine with Nystrm approximation technique and Universum data[J]. Neurocomputing， 2016， 175： 610-634. DOI： 10.1016/j.neucom.2015.10.102.

[7]朱昌明， 梅成就， 周日貴， 等. 基于Universum的多視角全局和局部結構風險最小化模型[J]. 上海海事大學學報， 2018， 39（3）： 91-102. DOI： 10.13340/j.jsmu.2018.03.017.

[8]劉鴻， 陳曉紅， 張恩豪. 融入Universum學習的度量學習算法[J]. 計算機工程與應用， 2019， 55（13）： 158-164， 238.

[9]CHEN Xiaohong， YIN Hujun， JIANG Fan， et al. Multi-view dimensionality reduction based on Universum learning[J]. Neurocomputing， 2018， 275： 2279-2286. DOI： 10.1016/j.neucom.2017.11.006.

[10]TENCER L， REZNAKOVA M， CHERIET M. UFuzzy： fuzzy models with Universum[J]. Applied Soft Computing， 2016， 59： 1-18. DOI： 10.1016/j.asoc.2016.05.041.

[11]CHEN Songcan， WANG Zhe， TIAN Yongjun. Matrix-pattern-oriented Ho-Kashyap classifier with regularization learning[J]. Pattern Recognition， 2016， 40（5）： 1533-1543. DOI： 10.1016/j.patcog.2006.09.001.

[12]BERGER A， GUDA S. Threshold optimization for F measure of macro-averaged precision and recall[J]. Pattern Recognition， 2020， 102： 107250. DOI： 10.1016/j.patcog.2020.107250.

[13]TANG Shijie， TSUI KW. Distributional properties for the generalized p-value for the Behrens-Fisher problem[J]. Statistics & Probability Letters， 2007， 77（11）： 1-8. DOI： 10.1016/j.spl.2006.05.005.

（編輯 賈裙平）