軟弱圍巖隧道鎖腳錨管力學(xué)特性現(xiàn)場模擬試驗(yàn)

石 州，羅彥斌，陳建勛，劉偉偉，于海濤

(1. 長安大學(xué) 公路學(xué)院，陜西 西安 710064；2. 廣東省交通集團(tuán)有限公司，廣東 廣州 510000)

0 引言

軟弱圍巖隧道開挖過程中，圍巖自穩(wěn)能力差，開挖工序繁雜，施工過程中極易發(fā)生鋼架扭曲、斷裂、噴射混凝土開裂、掉塊、仰拱隆起、二次襯砌開裂、掉塊，甚至垮塌等病害問題[1-4]。鎖腳錨管作為軟弱圍巖隧道建設(shè)中的一種常用支護(hù)手段，在控制隧道變形沉降和提高結(jié)構(gòu)穩(wěn)定性方面發(fā)揮了重要作用，其結(jié)構(gòu)簡單、操作方便、經(jīng)濟(jì)適用，因此被廣泛應(yīng)用于以分部開挖法施工的軟弱圍巖隧道工程建設(shè)中[5-6]。其結(jié)構(gòu)力學(xué)承載特性及合理支護(hù)參數(shù)的選取已經(jīng)成為國內(nèi)外隧道研究人員普遍關(guān)注和重點(diǎn)研究的問題[7-10]。

近些年來，國內(nèi)外專家學(xué)者和工程技術(shù)人員，通過理論分析[11-13]、數(shù)值模擬[14-16]和工程實(shí)踐等[17-23]方法對鎖腳錨管展開了一系列研究。黃彬等[18]根據(jù)中南鐵路的大量黃土隧道的施工經(jīng)驗(yàn)分析了鎖腳錨管控制隧道拱部下沉和水平收斂的作用效果，指出鎖腳錨管的打設(shè)長度和角度對隧道變形有顯著影響。賴金星等[19]通過對比相同地層中分別采用與不采用鎖腳錨管施工的隧道拱頂下沉與水平收斂的現(xiàn)場實(shí)測結(jié)果，證實(shí)了黃土隧道中鎖腳錨管可以有效控制隧道變形。王道遠(yuǎn)等[20]通過高地應(yīng)力隧道“剛性強(qiáng)支”下變形控制現(xiàn)場試驗(yàn)研究了鎖腳錨管在軟弱圍巖環(huán)境下的力學(xué)及變形特性。

盡管鎖腳錨管在軟弱圍巖隧道變形控制和大變形災(zāi)害處治中應(yīng)用廣泛，但目前對于鎖腳錨管的作用機(jī)理和受力特性的研究仍不夠全面和深入，尤其對于鎖腳錨管在圍巖荷載作用下的受力判別以及應(yīng)變和位移的分布變化規(guī)律等方面缺乏系統(tǒng)的研究，大多相關(guān)研究是采用數(shù)值模擬或者通過監(jiān)測隧道變形而間接反映鎖腳錨管的作用效果，缺乏對其更為直接、有針對性的試驗(yàn)研究，并且對于軟弱圍巖條件下鎖腳錨管的合理打設(shè)角度、長度等力學(xué)參數(shù)缺乏符合工程實(shí)際的定量化分析研究。同時，由于隧道中鎖腳錨管屬于隱蔽型的支護(hù)措施，結(jié)構(gòu)受力復(fù)雜，操作空間狹小，現(xiàn)有的結(jié)構(gòu)受力測試方法和傳感器無法直接應(yīng)用于鎖腳錨管的現(xiàn)場測試。因此，需要尋求一種能夠模擬隧道中鎖腳錨管實(shí)際傳力機(jī)制和準(zhǔn)確測量錨管力學(xué)及變形特性的試驗(yàn)方法，對復(fù)雜環(huán)境條件下鎖腳錨管的內(nèi)力分布規(guī)律及結(jié)構(gòu)變形特性進(jìn)行研究。

本試驗(yàn)借鑒傳感器外貼、導(dǎo)線內(nèi)引的思路，提出采用非電量電測法對鎖腳錨管的受力變形進(jìn)行測量，設(shè)計出一套可以模擬隧道中鋼架對鎖腳錨管豎向作用力的試驗(yàn)裝置，并在某隧道左洞附近邊坡對鎖腳錨管進(jìn)行了現(xiàn)場模擬試驗(yàn)。通過分析不同打設(shè)角度下鎖腳錨管的實(shí)測應(yīng)變及相應(yīng)的彎曲應(yīng)變，揭示了鎖腳錨管的內(nèi)力和變形分布及荷載響應(yīng)情況，并結(jié)合不同打設(shè)角度下鎖腳錨管端部位移和試驗(yàn)前后的變形情況，對鎖腳錨管的力學(xué)作用機(jī)理和結(jié)構(gòu)承載特性進(jìn)行了系統(tǒng)全面的研究。

1 鎖腳錨桿模擬試驗(yàn)設(shè)計

本試驗(yàn)選取與隧道圍巖土質(zhì)相同的黃土邊坡來模擬隧道圍巖，通過加載裝置在鎖腳錨管端部加載模擬鋼架對鎖腳錨管的豎向作用，采用在鎖腳錨管管壁外粘貼箔式電阻應(yīng)變片、導(dǎo)線內(nèi)引的方式測量管身應(yīng)變。本試驗(yàn)僅研究空心錨管在端部豎向荷載作用下管身的應(yīng)變分布特性及錨管變形規(guī)律，不考慮注漿效果的影響。為研究鎖腳錨管在不同打設(shè)角度下的力學(xué)特性，進(jìn)而研究鎖腳錨管的合理打設(shè)長度和角度及揭示鎖腳錨管的應(yīng)變與位移分布規(guī)律，本現(xiàn)場試驗(yàn)鎖腳錨管的打設(shè)角度分別為0°，30°，45°和60°。

1.1 試驗(yàn)錨管設(shè)計

為盡可能準(zhǔn)確地模擬隧道中的鎖腳錨管，本試驗(yàn)采用與剪子岔2號隧道中相同規(guī)格的無縫鋼管制作試驗(yàn)錨管。試驗(yàn)錨管相關(guān)物理力學(xué)參數(shù)如表1所示。選用量程為±20 000 με的BE120-5 AA電阻應(yīng)變片進(jìn)行錨管應(yīng)變監(jiān)測。試驗(yàn)錨管測點(diǎn)布置如圖1所示，每個斷面上測點(diǎn)布置圖如圖2所示。

表1 鎖腳錨管物理力學(xué)參數(shù)Tab.1 Mechanical parameters of foot-lock anchor pipe

圖1 錨管測點(diǎn)布置圖(單位:cm)Fig.1 Layout of measuring points on anchor pipe(unit:cm)

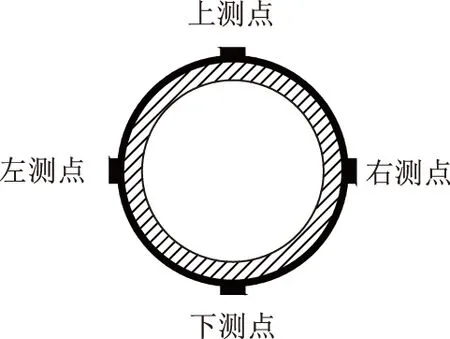
圖2 各斷面測點(diǎn)布置圖Fig.2 Layout of measuring points at each section

為降低鉆孔對錨管截面強(qiáng)度的影響，錨管測點(diǎn)截面圓周上、下孔與左、右孔2對鉆孔交錯布置；通過對應(yīng)變片粘貼位置的管壁進(jìn)行微拋光，并用脫脂棉沾取丙酮溶劑進(jìn)行擦洗來增加電阻應(yīng)變片與錨管管壁的接觸面積并避免貼好的應(yīng)變片脫膠；將應(yīng)變片的導(dǎo)線在管內(nèi)通過鉆孔穿引后，用電烙鐵將應(yīng)變片引線和導(dǎo)線在接線端子上焊接在一起并及時在測點(diǎn)處涂刷3～5 mm厚的環(huán)氧樹脂膠覆蓋應(yīng)變片、導(dǎo)線進(jìn)行保護(hù)；最后在鎖腳錨管進(jìn)孔端安裝一個長3 cm 錐底圓周直徑為51 mm的鋼錐頭，以保護(hù)鎖腳錨管內(nèi)部導(dǎo)線在整個試驗(yàn)過程中完好無損。具體流程如圖3所示。

圖3 試驗(yàn)錨管設(shè)計安裝Fig.3 Design and installation of test anchor pipe

為抵消沿錨管長度方向土體溫度不同而產(chǎn)生的誤差，本次試驗(yàn)取與錨管相同的鋼管制作了溫度補(bǔ)償塊，利用機(jī)床從鋼管上切割寬度為2 cm，L=2.5 m 的板條，將貼好應(yīng)變片的溫度補(bǔ)償塊放置在L=2.5 m，φ26 mm，壁厚為2 mm的鍍鋅管內(nèi)。

1.2 現(xiàn)場試驗(yàn)

隧址區(qū)位于陜北黃土高原南部，地貌以黃土臺塬、黃土梁峁-溝壑為主。隧道圍巖由上更新統(tǒng)馬蘭組黃土(Q3col)組成，圍巖單一，為Ⅴ級圍巖。本試驗(yàn)的試驗(yàn)場地為黃(陵)延(安)高速剪子岔二號隧道左洞洞口附近的高陡邊坡，試驗(yàn)以與隧道圍巖土質(zhì)相同的邊坡模擬圍巖，試驗(yàn)區(qū)域的土層為上更新統(tǒng)馬蘭組黃土(Q3col)，濕陷性不明顯，自然邊坡整體穩(wěn)定性好，土體呈硬塑狀。現(xiàn)場對試驗(yàn)邊坡黃土取樣并進(jìn)行室內(nèi)試驗(yàn)測定，土樣的工程性質(zhì)指標(biāo)如表2所示。

表2 圍巖土體工程指標(biāo)參數(shù)Tab.2 Engineering parameters of surrounding rock soil

為了避免相鄰鎖腳錨管在試驗(yàn)加載過程中產(chǎn)生相互影響，相鄰兩鉆孔中心間距設(shè)置為100 cm，采用鉆頭直徑為70 mm的TY28型號鉆機(jī)現(xiàn)場鉆取了4根不同角度的錨管試驗(yàn)鉆孔，同時用同樣方法鉆取角度為30°的溫度補(bǔ)償塊埋設(shè)鉆孔；安設(shè)好的錨管與溫度補(bǔ)償塊均靜置1 h以上，并在此時間段內(nèi)進(jìn)行零漂檢測。

現(xiàn)場試驗(yàn)時通過自主研發(fā)的加載裝置和反力裝置在鎖腳錨管端部豎向加載模擬鋼架對鎖腳錨管的豎向作用，通過錨管端部施加荷載的層級變化來模擬鎖腳錨管在不同埋深及不同荷載條件下的力學(xué)承載機(jī)制，如圖6所示。鎖腳錨管管身應(yīng)變采用電阻應(yīng)變片測試，應(yīng)變數(shù)據(jù)通過TST3821E無線遙測靜態(tài)電阻應(yīng)變儀采集；錨管端部位移采用SW-40型手持式激光測距儀并結(jié)合白紙描點(diǎn)測量，如圖7所示。

圖6 加載裝置及反力裝置安裝Fig.6 Installation of loading device and reaction device

圖7 端部位移測量儀器布置Fig.7 Arrangement of measuring instrument for end displacement

2 鎖腳錨模擬試驗(yàn)結(jié)果分析

模擬試驗(yàn)測試結(jié)束后，通過統(tǒng)計測試數(shù)據(jù)發(fā)現(xiàn)，4根鎖腳錨管共80個測點(diǎn)以及溫度補(bǔ)償塊上的5個測點(diǎn)均成活(成活率100%)，說明采用“外貼內(nèi)引法”和非電量電測法進(jìn)行鎖腳錨管應(yīng)變測試是可行的。以下對試驗(yàn)數(shù)據(jù)進(jìn)行分析。

2.1 鎖腳錨管各斷面測點(diǎn)應(yīng)變分布變化規(guī)律

鎖腳錨管各斷面測點(diǎn)應(yīng)變實(shí)際上是拉(壓)彎組合應(yīng)變，其分布變化規(guī)律主要從兩個方面進(jìn)行分析，即各級荷載作用下鎖腳錨管的測點(diǎn)應(yīng)變沿錨管長度的分布規(guī)律和鎖腳錨管各方位測點(diǎn)應(yīng)變隨端部荷載的變化規(guī)律。同時根據(jù)隧道工程中鎖腳錨管以豎向變形為主的承載作用機(jī)制，本試驗(yàn)中僅對鎖腳錨管橫截面上下部應(yīng)力應(yīng)變分布規(guī)律進(jìn)行重點(diǎn)分析研究。下面分別對這兩個方面測點(diǎn)應(yīng)變的分布變化規(guī)律進(jìn)行分析。

2.1.1 各級荷載下測點(diǎn)應(yīng)變沿錨管長度的分布規(guī)律

(1) 各級荷載下上部測點(diǎn)應(yīng)變沿錨管長度的分布規(guī)律

圖8～圖11分別為不同打設(shè)角度的鎖腳錨管在各級荷載作用下其上部測點(diǎn)的應(yīng)變沿錨管長度的分布情況，因上部及下部應(yīng)變對稱分布，此處僅以上部應(yīng)變?yōu)槔M(jìn)行分析。

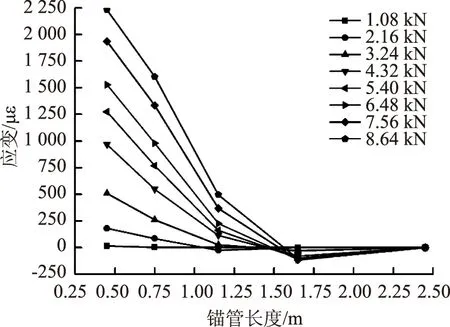
圖8 0°打設(shè)錨管上部測點(diǎn)應(yīng)變沿錨管長度分布曲線Fig.8 Curves of strain distribution at upper measuring point along length of anchor pipe at 0° angle

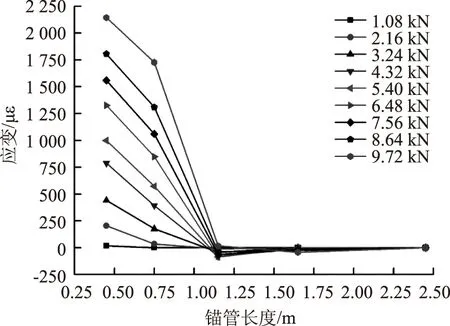
圖9 30°打設(shè)錨管上部測點(diǎn)應(yīng)變沿錨管長度分布曲線Fig.9 Curves of strain distribution at upper measuring point along length of anchor pipe at 30° angle

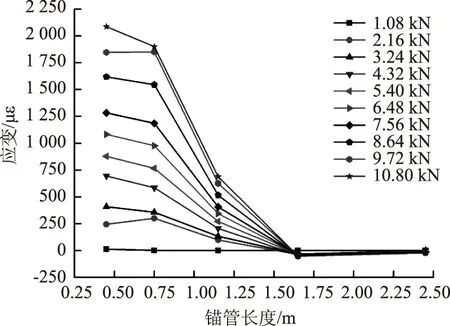
圖10 45°打設(shè)錨管上部測點(diǎn)應(yīng)變沿錨管長度分布曲線Fig.10 Curves of strain distribution at upper measuring point along length of anchor pipe at 45° angle

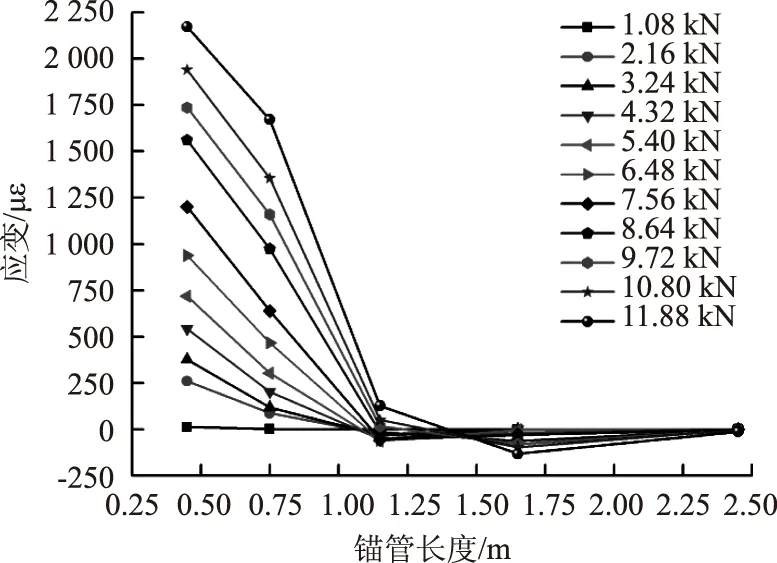
圖11 60°打設(shè)錨管上部測點(diǎn)應(yīng)變沿錨管長度分布曲線Fig.11 Curves of strain distribution at upper measuring point along length of anchor pipe at 60° angle

對于上部測點(diǎn)的應(yīng)變，由圖8～圖11可知：(1) 打設(shè)角度相同時，各級荷載作用下鎖腳錨管上部測點(diǎn)應(yīng)變沿錨管長度的分布規(guī)律基本一致，即在斷面1處為最大正應(yīng)變，隨著錨管長度的增加應(yīng)變迅速衰減直至減為0，然后應(yīng)變變?yōu)樨?fù)應(yīng)變并沿著錨管長度緩慢變化最終趨于0；(2) 當(dāng)荷載相同時，錨管相同位置處的測點(diǎn)應(yīng)變大小隨著打設(shè)角度的增大而減小；(3) 鎖腳錨管端部荷載傳遞長度因錨管打設(shè)角度不同而異，當(dāng)鎖腳錨管的打設(shè)角度為45°時，端頭荷載傳遞長度最大，此角度打設(shè)的鎖腳錨管能更好地將荷載傳遞到圍巖中且鎖腳錨管受力相對更加均勻。

2.1.2 各斷面不同方位處測點(diǎn)應(yīng)變隨錨管端部荷載的變化規(guī)律

(1)鎖腳錨管0°打設(shè)時不同方位測點(diǎn)荷載-應(yīng)變分布規(guī)律

圖12為打設(shè)角度0°時鎖腳錨管不同方位測點(diǎn)荷載-應(yīng)變分布情況。

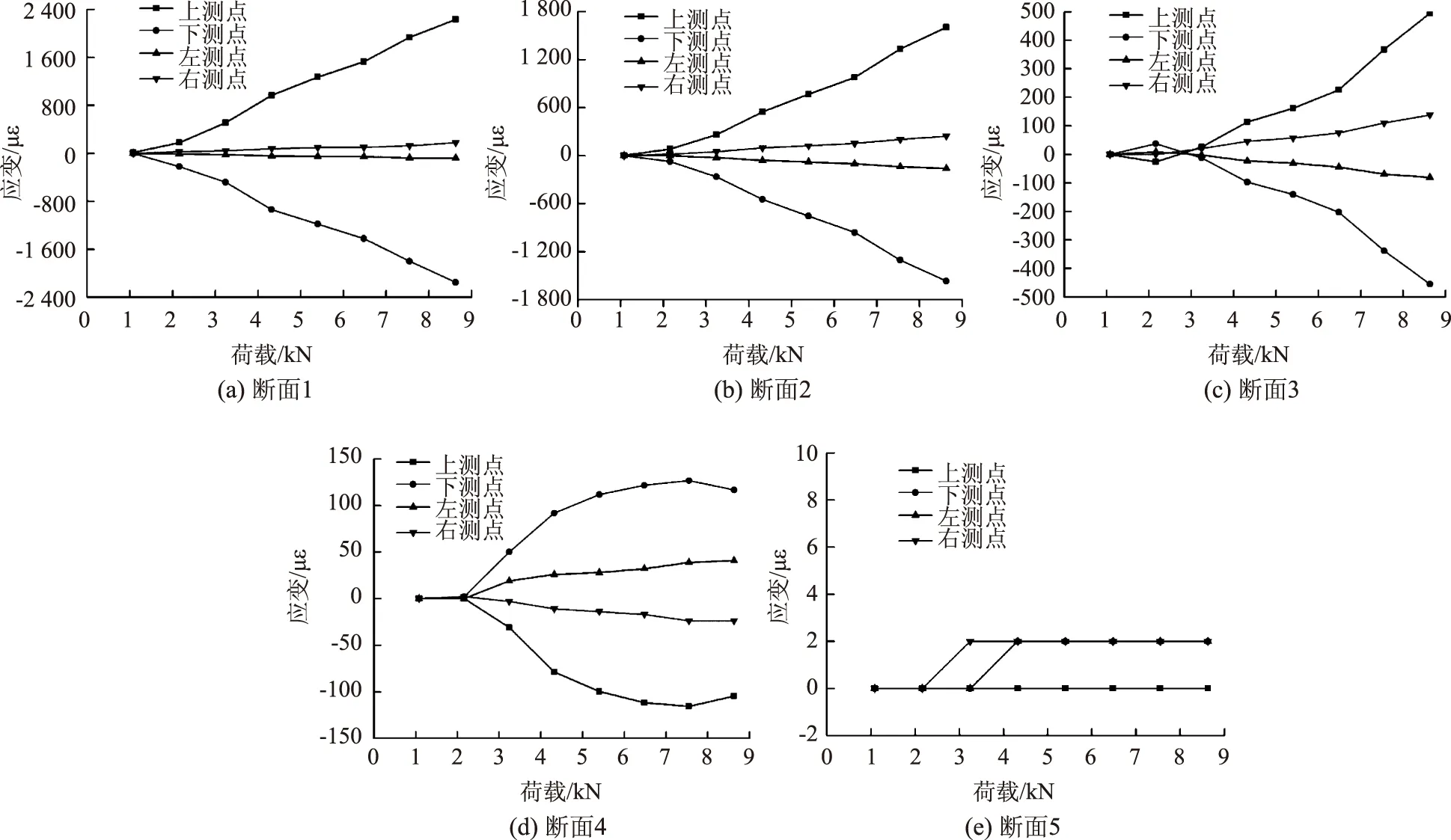
圖12 0°打設(shè)錨管不同方位測點(diǎn)荷載-應(yīng)變分布曲線Fig.12 Load-strain distribution curves of measurement points on anchor pipe at 0° angle

對于打設(shè)角度為0°的鎖腳錨管，由圖12可知：①鎖腳錨管5個斷面中各測點(diǎn)應(yīng)變在數(shù)值上與端部荷載基本呈正相關(guān)；②同一荷載下，各個測點(diǎn)均為斷面1(靠近加載點(diǎn))應(yīng)變值最大，斷面5(遠(yuǎn)離加載點(diǎn))應(yīng)變值最小，且從斷面1到斷面5應(yīng)變值遞減，說明鎖腳錨管將其承受的端部豎向荷載沿其長度方向逐漸向圍巖深部傳遞；③同一荷載下，同一斷面的上、下測點(diǎn)應(yīng)變值均遠(yuǎn)遠(yuǎn)大于左、右測點(diǎn)的應(yīng)變值，且上、下測點(diǎn)應(yīng)變值大小相近，說明鎖腳錨管主要依靠其豎向彎折變形來承受荷載；④斷面5的測點(diǎn)應(yīng)變很小(2 με)，可以忽略不計，說明荷載傳遞到錨管底部附近時已經(jīng)消散殆盡，所以對于0°打設(shè)的鎖腳錨管，長度2.5 m能夠滿足承載要求。

(2)鎖腳錨管30°打設(shè)時不同方位測點(diǎn)荷載-應(yīng)變分布規(guī)律

圖13為打設(shè)角度30°時鎖腳錨管不同方位測點(diǎn)應(yīng)變荷載-應(yīng)變分布情況。

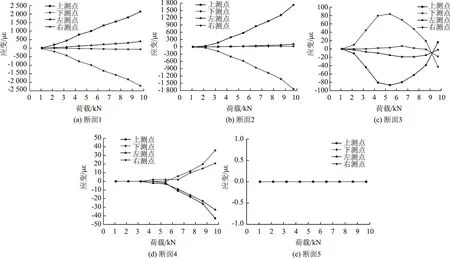
圖13 30°打設(shè)錨管不同方位測點(diǎn)荷載-應(yīng)變分布規(guī)律Fig.13 Load-strain distribution rules of measurement points on anchor pipe at 30° angle

對于打設(shè)角度為30°的鎖腳錨管，由圖13可知：① 斷面1、斷面2和斷面4上各個測點(diǎn)應(yīng)變在數(shù)值上與端頭荷載基本呈正相關(guān)，而斷面3的測點(diǎn)應(yīng)變隨著荷載先增大到峰值后逐漸減小，說明斷面3處錨管隨著受力和變形的持續(xù)進(jìn)行，其承載方式發(fā)生了改變(先加載后卸載)；② 同一荷載下，各測點(diǎn)的應(yīng)變值基本呈現(xiàn)為從斷面1(靠近加載點(diǎn))到斷面5(遠(yuǎn)離加載點(diǎn))逐級遞減的分布規(guī)律，說明鎖腳錨管將其承受的端部豎向荷載沿其長度方向逐漸向圍巖深部傳遞；③同一荷載下，同一斷面的上、下測點(diǎn)應(yīng)變值基本均大于左、右測點(diǎn)的應(yīng)變值，且對于斷面1和斷面2，上、下測點(diǎn)應(yīng)變遠(yuǎn)遠(yuǎn)大于左右測點(diǎn)應(yīng)變，說明鎖腳錨管尤其是靠近加載端的部分主要依靠其豎向彎折變形來承受荷載；④斷面5的測點(diǎn)應(yīng)變?yōu)?，說明錨管尾端部分并未承受荷載，所以對于30°打設(shè)的鎖腳錨管，長度2.5 m能夠滿足承載要求。

(3)鎖腳錨管45°打設(shè)時不同方位測點(diǎn)荷載-應(yīng)變分布規(guī)律

圖14為打設(shè)角度為45°時鎖腳錨管不同方位測點(diǎn)荷載-應(yīng)變分布情況。

對于打設(shè)角度為45°的鎖腳錨管，由圖14可知：①斷面1、斷面2和斷面3各測點(diǎn)應(yīng)變在數(shù)值上與端頭荷載基本呈正相關(guān)。斷面4和斷面5的各測點(diǎn)應(yīng)變均較小；②同一荷載下，各測點(diǎn)的應(yīng)變值基本呈現(xiàn)為從斷面1(靠近加載點(diǎn))到斷面5(遠(yuǎn)離加載點(diǎn))逐級遞減的分布規(guī)律，說明鎖腳錨管將其承受的端部豎向荷載沿其長度方向逐漸向圍巖深部傳遞；③同一荷載下，前3個斷面的上、下測點(diǎn)應(yīng)變值均遠(yuǎn)遠(yuǎn)大于左、右測點(diǎn)的應(yīng)變值，說明鎖腳錨管尤其是靠近加載端的部分主要依靠其豎向彎折變形來承受荷載；④斷面5各測點(diǎn)應(yīng)變最大值為-20 με左右，應(yīng)變值較小，可以忽略不計，所以對于45°打設(shè)鎖腳錨管，長度2.5 m能夠滿足承載要求。

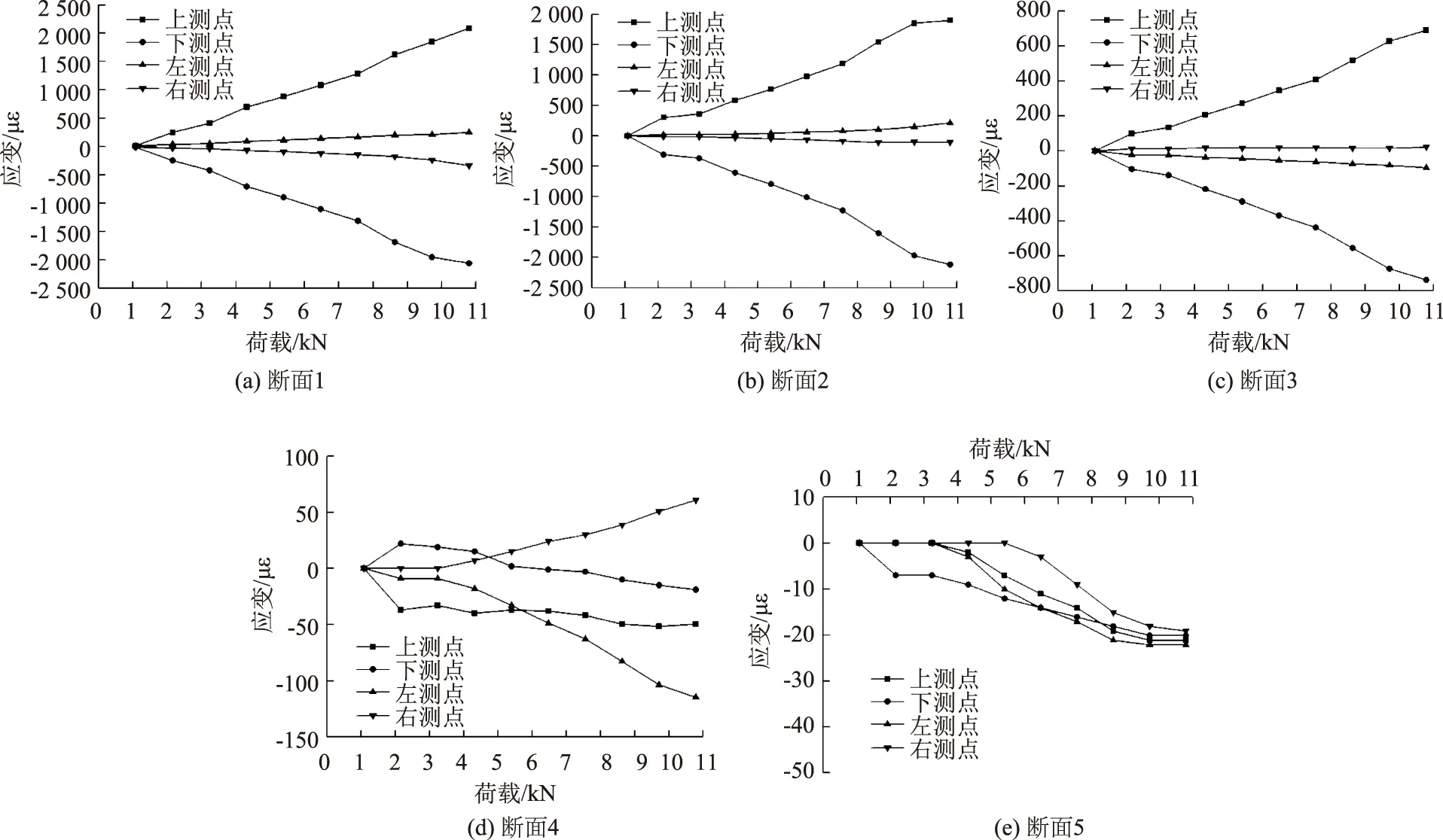
圖14 45°打設(shè)錨管不同方位測點(diǎn)荷載-應(yīng)變分布曲線Fig.14 Load-strain distribution curves of measurement points on anchor pipe at 45° angle

(4)鎖腳錨管60°打設(shè)時不同方位測點(diǎn)荷載-應(yīng)變分布規(guī)律

圖15為打設(shè)角度為60°時鎖腳錨管不同方位測點(diǎn)荷載-應(yīng)變分布情況。

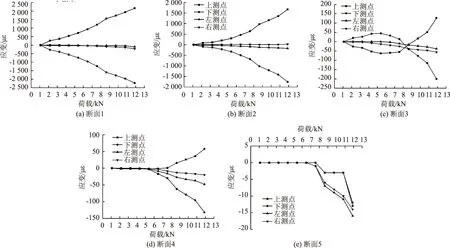
圖15 60°打設(shè)錨管不同方位測點(diǎn)荷載-應(yīng)變分布曲線Fig.15 Load-strain distribution curves of measurement points on anchor pipe at 60° angle

對于打設(shè)角度為60°的鎖腳錨管，由圖15可知：①斷面1和斷面2各測點(diǎn)應(yīng)變在數(shù)值上與端頭荷載基本呈正相關(guān)；②同一荷載下，各個測點(diǎn)的應(yīng)變值基本呈現(xiàn)為斷面1(靠近加載點(diǎn))到斷面5(遠(yuǎn)離加載點(diǎn))逐級遞減的分布規(guī)律，說明鎖腳錨管將其承受的端部豎向荷載沿其長度方向逐漸向圍巖深部傳遞；③同一荷載下，前4個斷面的上、下測點(diǎn)應(yīng)變值基本均遠(yuǎn)遠(yuǎn)大于左、右測點(diǎn)的應(yīng)變值，說明鎖腳錨管尤其是靠近加載端的部分主要依靠其豎向彎折變形來承受荷載；④斷面5的測點(diǎn)最大應(yīng)變?yōu)?15 με左右，應(yīng)變值較小，所以對于60°打設(shè)鎖腳錨管，長度2.5 m能夠滿足承載要求。

綜合圖16～圖19，可以得到不同打設(shè)角度下鎖腳錨管測點(diǎn)應(yīng)變隨端部荷載的變化規(guī)律如下：①不同打設(shè)角度下各鎖腳錨管均表現(xiàn)為其各個斷面的測點(diǎn)應(yīng)變隨著荷載的增加而隨之增大，說明鎖腳錨管能有效對其端部荷載作出響應(yīng)；②相同荷載下，各測點(diǎn)應(yīng)變值從斷面1到斷面5遞減，上、下測點(diǎn)應(yīng)變值一般遠(yuǎn)遠(yuǎn)大于左、右測點(diǎn)的應(yīng)變值，說明鎖腳錨管能有效將其承受的端部豎向荷載沿其長度方向逐漸向圍巖深部傳遞，且錨管主要靠其距加載點(diǎn)較近部分的豎向彎折變形承受荷載；③在同一端部荷載下，隨著打設(shè)角度的增大，各錨管的最大應(yīng)變值相應(yīng)減小，且應(yīng)變?yōu)?的斷面位置逐漸向錨管深部位置移動，說明增大鎖腳錨管的打設(shè)角度有利于將端部豎向荷載傳遞至圍巖深處；④無論鎖腳錨管以小角度(0°和30°)打設(shè)還是大角度(45°和60°)打設(shè)，端部荷載傳遞至錨管1.5 m位置左右時管身應(yīng)變已衰減至很小，且管尾處應(yīng)變可忽略不計，所以鎖腳錨管的打設(shè)長度可取為2.5 m左右。

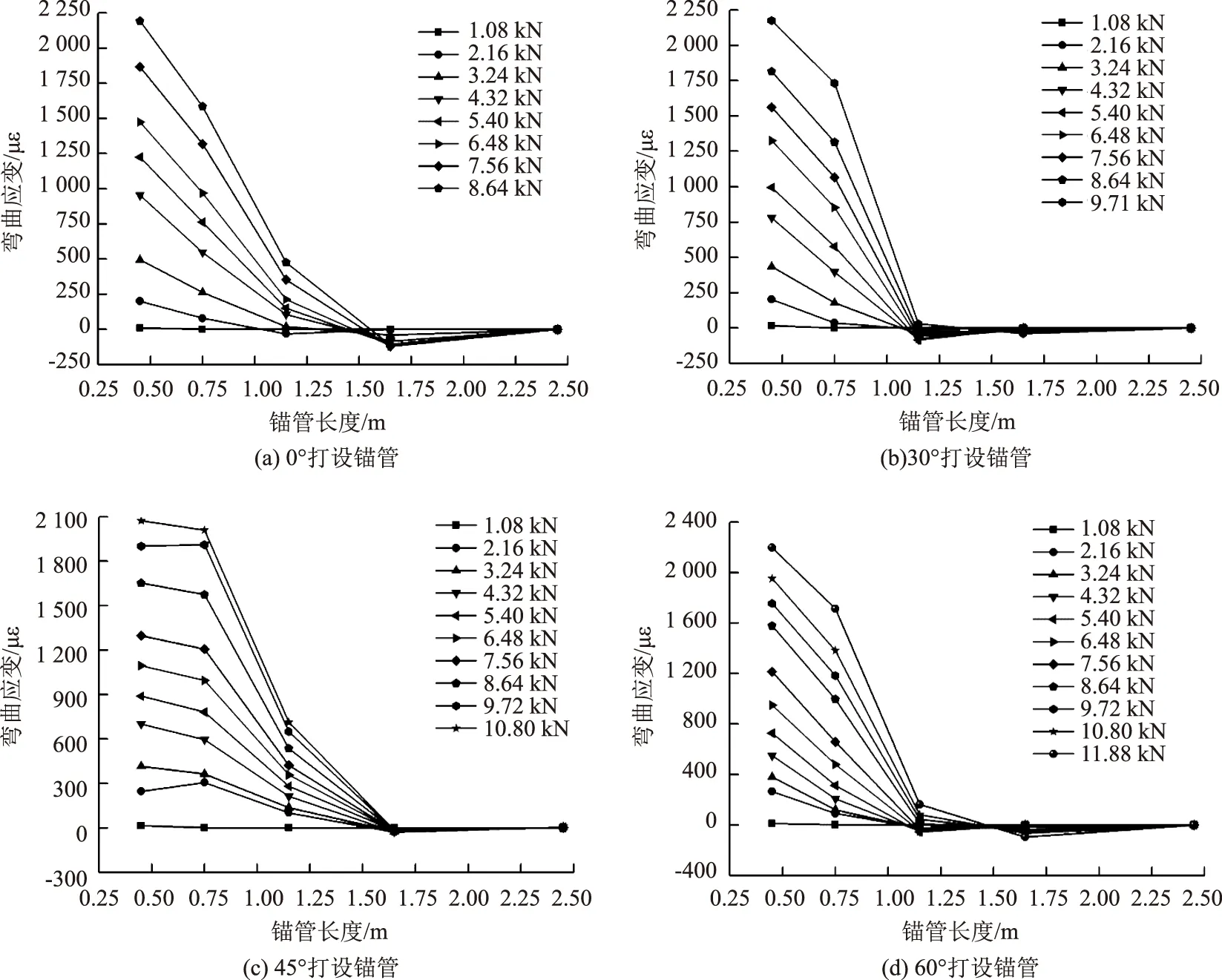
圖16 鎖腳錨管上下彎曲應(yīng)變沿錨管長度分布曲線Fig.16 Distribution curves of bending strains of upper and lower parts of foot-lock anchor pipe along pipe length

2.2 鎖腳錨管各斷面彎曲應(yīng)變的分布變化規(guī)律

根據(jù)材料力學(xué)及錨桿軸力分析可知，各斷面的上下彎曲應(yīng)變可由式(1)計算得到：

(1)

下面根據(jù)各測點(diǎn)應(yīng)變對彎曲應(yīng)變進(jìn)行計算，并對其分布規(guī)律進(jìn)行分析。

2.2.1 各級荷載下彎曲應(yīng)變沿錨管長度的分布規(guī)律

圖16(a)～(d)分別為不同打設(shè)角度下鎖腳錨管各斷面上下彎曲應(yīng)變沿錨管長度的分布情況。

對于鎖腳錨管上下彎曲應(yīng)變，由圖16(a)～(d)可知：(1) 打設(shè)角度一定時，各級荷載作用下鎖腳錨管上下彎曲應(yīng)變沿錨管長度的分布規(guī)律基本一致，即彎曲應(yīng)變隨著錨管長度的增加而迅速衰減直至趨于零，說明錨管主要為其加載點(diǎn)附近的部分管段承受彎矩。(2)當(dāng)荷載相同時，對于同一斷面，其上下彎曲應(yīng)變值隨著打設(shè)角度的增大而減小，其原因是隨著打設(shè)角度的增大，豎向荷載在錨管端部的橫向分力隨之減小，這一分布規(guī)律表明增大鎖腳錨管的打設(shè)角度有助于減小其管身的豎向彎矩。(3)鎖腳錨管端部荷載的傳遞長度因錨管打設(shè)角度而異，此處用上下彎曲應(yīng)變第一零點(diǎn)長度來衡量(某一荷載作用下彎曲應(yīng)變?yōu)榱銓?yīng)的斷面的最小錨管長度)，打設(shè)角度分別為0°，30°，45°和60°時，荷載為8.64 kN對應(yīng)彎曲應(yīng)變第一零點(diǎn)長度分別為1.50，1.15，1.65和1.40 m，容易得知，當(dāng)鎖腳錨管的打設(shè)角度為45°時，端部荷載的傳遞長度最大，此時鎖腳錨管的豎向承載力發(fā)揮得最極致。

2.2.2 各個斷面的彎曲應(yīng)變隨端部荷載的變化規(guī)律

(1) 鎖腳錨管各斷面上下彎曲應(yīng)變隨端部荷載的分布規(guī)律

圖17(a)～(d)分別為不同打設(shè)角度下鎖腳錨管各斷面上下彎曲應(yīng)變隨端部豎向荷載的分布情況。

對于鎖腳錨管各斷面上下彎曲應(yīng)變，由圖17(a)～(d)可知：(1) 任意打設(shè)角度下，鎖腳錨管各個斷面的上下彎曲應(yīng)變在數(shù)值上與端部荷載基本呈正相關(guān)。(2) 同一打設(shè)角度時，各斷面上下彎曲應(yīng)變值隨著斷面距離加載點(diǎn)的距離增大而減小，說明鎖腳錨管能有效將其承受的端部豎向荷載沿其長度方向逐漸向圍巖深部傳遞。(3) 斷面1和斷面2的上下彎曲應(yīng)變遠(yuǎn)遠(yuǎn)大于其他3個斷面的彎曲應(yīng)變，說明鎖腳錨管主要靠加載端部附近部分承受彎矩。(4) 在相同的端部荷載下，鎖腳錨管同一斷面處的上下彎曲應(yīng)變隨著打設(shè)角度的增大而減小，說明增大鎖腳錨管的打設(shè)角度有助于改善鎖腳錨管的彎矩受力狀態(tài)。

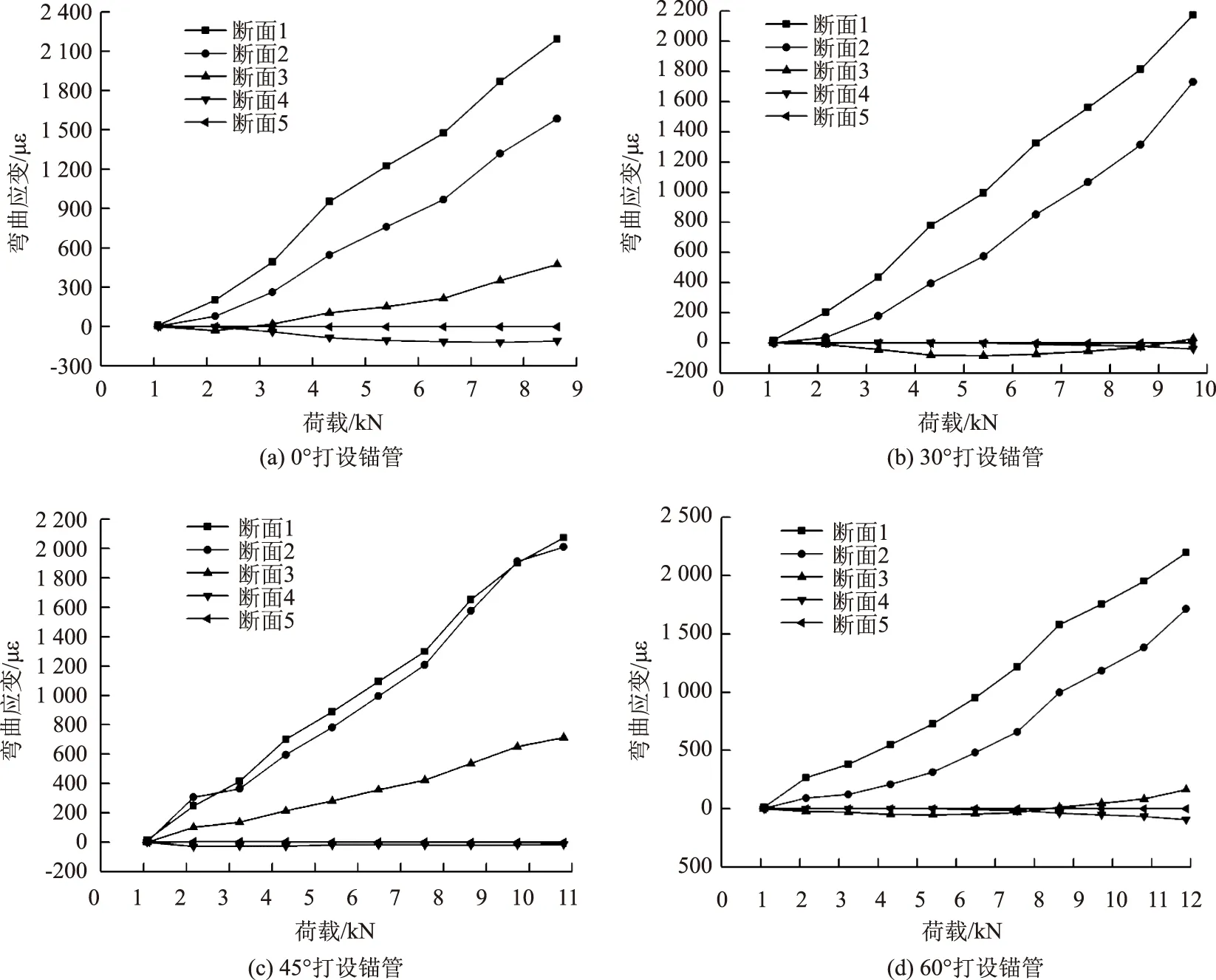
圖17 鎖腳錨管上下彎曲應(yīng)變隨端部荷載的變化曲線Fig.17 Distribution curves of bending strains of upper and lower parts of foot-lock anchor pipe varying with end load

2.3 鎖腳錨管端部水平位移隨端部荷載的變化規(guī)律

不同端部荷載作用下鎖腳錨管的端部水平位移如圖18所示。

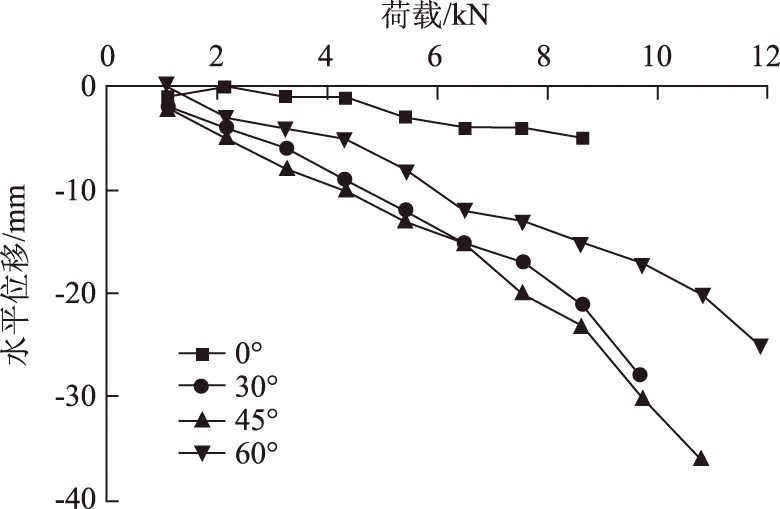
圖18 鎖腳錨管端部水平位移隨荷載的變化曲線Fig.18 curves of horizontal displacement at end of foot-lock anchor pipe varying with load

對于各端部荷載作用下鎖腳錨管的端部水平位移，由圖18可知：(1) 對于打設(shè)角度為30°，45°和60°的鎖腳錨管，其端部水平位移隨著荷載的走勢基本一致，且在加載前期，錨管端頭水平位移增速都較慢，隨著荷載的逐漸增大，水平位移增速相應(yīng)增大，說明隨著荷載的持續(xù)施加和增大，錨管的彎曲變形和管周圍巖的破壞進(jìn)入了快速演變階段。(2) 當(dāng)荷載相同時，錨管端部水平位移隨著打設(shè)角度的不同而不同，當(dāng)打設(shè)角度為45°時其水平位移為最大，打設(shè)角度為0°時其水平位移為最小。

2.4 試驗(yàn)前后鎖腳錨管與圍巖變形對比分析

為了更好地研究鎖腳錨管整體的變形破壞特點(diǎn)，試驗(yàn)結(jié)束后，利用挖掘機(jī)將試驗(yàn)錨管整體小心挖出。以下對鎖腳錨管的變形情況和圍巖的破壞情況進(jìn)行分析研究。圖19為不同打設(shè)角度下鎖腳錨管試驗(yàn)前后的變形對比圖。圖20為圍巖孔口附近試驗(yàn)前后的變形破壞對比圖。

圖20 試驗(yàn)前后圍巖對比Fig.20 Comparison of surrounding rock states before and after test

由圖19可知，鎖腳錨管的變形主要在靠近加載點(diǎn)的一定管身范圍內(nèi)發(fā)生彎折變形。經(jīng)測量，折彎點(diǎn)均位于距錨管端部55 cm左右的位置，說明鎖腳錨管主要靠其孔口附近部分承受荷載。建議在隧道鎖腳錨管施工過程中注意保護(hù)孔口附近的圍巖，必要時可以采用一定的施工措施如圍巖注漿等方法對圍巖進(jìn)行加固。

由圖20可知，孔口附近均發(fā)生了不同程度的圍巖剝離破壞，且破壞區(qū)域主要集中在鉆孔的下部，說明孔口附近圍巖主要是在鎖腳錨管的豎向擠壓下產(chǎn)生了塑性變形和剝離破壞，所以隧道鎖腳錨管施工時應(yīng)注意保護(hù)孔口附近圍巖，最好對孔口附近尤其鉆孔下部圍巖施加適當(dāng)?shù)难a(bǔ)強(qiáng)措施。

3 結(jié)論

本研究根據(jù)現(xiàn)場模擬試驗(yàn)對鎖腳錨管的力學(xué)作用機(jī)理和結(jié)構(gòu)承載特性進(jìn)行了系統(tǒng)全面的分析研究，主要結(jié)論如下：

(1)不同打設(shè)角度下鎖腳錨管各方位測點(diǎn)應(yīng)變沿錨管長度的分布規(guī)律與不同荷載下各測點(diǎn)應(yīng)變的變化規(guī)律基本一致，均為加載端的錨管應(yīng)變較大并沿管身向圍巖深部遞減。同時，隨著打設(shè)角度的增大，各錨管應(yīng)變峰值隨之減小，應(yīng)變峰值部位與管端距離隨之變大，大角度打設(shè)的鎖腳錨管受力更均勻，且將端部荷載傳遞到圍巖更深部位置。不同打設(shè)角度下鎖腳錨桿末端應(yīng)變值均接近于0，因此鎖腳錨管打設(shè)長度取為2.5 m左右可滿足工程建設(shè)要求。

(2)在端部豎向荷載作用下，鎖腳錨管的彎曲應(yīng)變隨著錨管長度增加而迅速衰減，鎖腳錨管主要靠管口附近部位抵抗彎矩。鎖腳錨管的上下彎曲應(yīng)變曲線和測點(diǎn)應(yīng)變曲線在走勢及數(shù)值大小上均較為接近，鎖腳錨管在端部豎向荷載作用下主要依靠其豎向抗彎剛度提供承載力。

(3)鎖腳錨管端部水平位移隨著荷載的走勢基本一致，在加載前期錨管端頭水平位移增速均較慢，隨著荷載的逐漸增大，水平位移增速相應(yīng)增大。當(dāng)荷載相同時，錨管端部水平位移隨著打設(shè)角度的不同而不同，當(dāng)打設(shè)角度為45°時其水平位移為最大，打設(shè)角度為0°時其水平位移為最小。

(4)鎖腳錨管的變形破壞主要為集中在孔口附近的彎折破壞，鎖腳錨管主要依靠其抗彎剛度提供承載力。孔口圍巖的塑性變形和剝離破壞集中在錨管下方部位，主要由錨管的豎向擠壓變形引起。因此鎖腳錨管施工時應(yīng)注意保護(hù)孔口部位(尤其是鉆孔下部)圍巖的完整與強(qiáng)度，必要時可對孔口附近圍巖進(jìn)行加固。