深挖解題思路 促進思維提升
——等效電源法解決電路四類問題的分析

貴州 楊 勇 許 昊

高中階段常見的電路問題主要有四類，分別為電路的動態分析、電路中某用電器的功率計算、電學實驗電路、非線性電路的分析。這四類問題主要考查的是計算極值問題、誤差分析，所以常涉及等效電源或者內阻的計算方法，本文將從等效電源、內阻的計算方法入手，應用等效電源法分析上述的四類問題，為解決物理復雜問題提供有效的途徑。

一、問題的提出

在處理電路動態分析和求電源電動勢及內阻時，大部分同學習慣應用數學函數形式求解極值問題或者應用數學方程分析實驗誤差，這種方法對于初學者來說，不失為好方法，但是在處理高考試題中數學運算過于復雜，計算繁瑣，解題效率不高。同時如果數學計算能力薄弱，往往計算不能得到正確的結果。而電路的動態分析及測量電源電動勢是高考中的重點，那么尋一條“捷徑”可以使上述問題變得簡單，顯然研究和分析“等效電源”對突破以上問題和打破學生常規思維尤為重要。

二、等效電源的理解和分析

在處理高中物理問題時，當電路比較復雜，我們常把某些定值電阻與電源看成一個整體，研究其他電阻的相應的參量或者變化情況，也就是說把該定值電阻與電源看成一個整體，這就是等效電源。如圖1所示，等效電源的電動勢等于AB端開路時的電壓UAB，內阻等于從AB端看去電源與定值電阻串聯或并聯的總阻值，短路電流等于把AB直接短接的電流。

圖1

1.等效電源的電動勢的計算

如圖2所示的電路圖，電阻R1=R2=2 Ω，電源電動勢E=4 V，內阻r=1 Ω，求當R的阻值多大時消耗的功率最大？

圖2

【方法一】數學方法

為了方便體現數學方法復雜，這里將部分數據代入公式

【評價】數學函數討論在處理物理問題時，不失為一種好方法，但是如果考生的數學基礎不牢固，沒有寫出正確的關系式，可能計算出錯誤的答案；在應用數學方法討論電路問題時，第一：必須掌握電路的基本結構，正確判斷電路的串、并聯關系；第二：掌握閉合電路歐姆定律的書寫方法及部分電路的歐姆定律的應用，同時區分純電阻與非純電阻。

【方法二】等效電源法

圖3

圖4

【評價】對于等效電源電動勢的計算，根據戴維南定理及電路的結構情況，計算等效電動勢比較容易，也不容易算錯，但是對于等效內阻，在電路較為復雜時，等效內阻是不容易計算出來的，并且不注意就容易弄錯。等效電動勢按照等效電源的原理，若Uab為某電阻的電壓，則等效電動勢就等于該電壓，這與常規的電路計算方法一致，一般初學者也不會弄錯。

2.等效電源的內阻的深入分析

如圖5，電阻R1=R2=R3=2 Ω，電源電動勢E=4 V，內阻r=1 Ω，當求R消耗的最大功率時，又怎樣用等效電源法求解等效電源電動勢和內阻呢？

圖5

圖6

那么等效內阻r等等于多少呢，這里有的同學可能認為等于R1和r串聯后與R2并聯的總電阻，這里顯然是不對的，下面從兩個角度來分析和計算等效電源的內阻。

圖7

【總結】等效內阻的電路圖計算方法，等效的位置直接短接，從電源往外電路看，按照并、串聯電路的電阻計算方法即可。

圖8

【評價】對于等效電源內阻的計算，兩種方法可以通用，根據具體情況選擇適當的方法，當電路比較明確時可以直接應用方法二；當容易計算出等效電源和等效短路電流時選擇方法一。但是在練習時，可以嘗試兩種方法的一致性，有助于思維的拓展，解題能力的提升。

三、等效電源法在四種常見電路問題中的應用

從以往的高考試題來看，常見的電路問題主要有電路的動態分析、求極值問題、電學實驗電路、非線性電路的分析，如果用常規的方法，數學表達式有時很復雜，那么等效電源法具有把復雜問題簡單化的優勢，下面將應用等效電源的方法分析上述的四類問題。

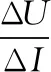
圖9

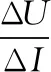
由于整個電路中，除了滑動變阻器R外，其余電阻不變。根據閉合電路的特點，路端電壓的變化與總電流的變量比值的絕對值等于電源的內阻，則圖9的電路也可以把滑動變阻器R看成外電阻，其余的電阻與電源看成等效電源，如圖10所示，虛線部分為等效電源的內部電路結構，則等效電源的內阻

圖10

【評價】等效電源法處理電路的動態分析，只要分清電路結構，理解等效電源思想，此方法處理電路動態分析相比傳統的列數學表達式算出變化量的方法，具有計算方便、高效解題的優勢。因此在備考或者練習時，適當介紹等效電源的思維，有助于學生思維的發散性和靈活性。

2.求解可變電阻的最大功率問題

【例2】如圖11，電源電動勢E=2 V，內阻r=3 Ω，電阻R1=1 Ω，電阻R2=4 Ω，R為滑動變阻器，當R取何值時R的功率達到最大值，最大值為多少？

圖11

圖12

3.“測電源電動勢與內阻”實驗的誤差分析

如圖13，甲、乙兩電路原理圖是高中物理教材中測電源電動勢及內阻的基本原理實驗電路圖，兩種實驗方法測電源內阻時都存在一定的誤差。通常的誤差分析應用的方法是數學方法，寫出理論值的數學表達式和實際值的數學表達式，通過比較即可得到測量值與真實值的差別；其次是應用圖像法，由閉合電路歐姆定律E=U+Ir，所以U=-Ir+E，作U-I圖線，圖線的斜率的絕對值|k|=r，縱截距為U=E。以上兩種誤差分析是測電源電動勢及內阻的基本方法，但是數學表達式的推導比較復雜，而作圖也掌握技巧和原理，對學生來說都存在一定的困難。

甲

如果能掌握等效電源的原理，應用等效電源的方法分析以上兩個實驗電路原理出現的誤差，會使問題變得簡單，過程簡捷。

圖14

對于乙圖，當電流表的電流為零時，電壓表的電流也為零，如圖15所示，電壓表兩端的電壓等于電源電動勢，則U=E，所以測得的電源電動勢沒有誤差；對于內阻，測得的內阻實際上是如圖15的等效內阻，所以有r測=RA+r，所以r測>r，測得的內阻大于實際的內阻，所以偏大。

圖15

【評價】對于應用等效電源方法分析“測電源電動勢和內阻”的實驗，除了以上的兩種電路原理圖之外，其他原理都可以應用等效電源的方法分析，主要掌握等效電源的方法，即可應用自如。

4.等效電源法分析非線性元件的功率問題

非線性元件在高中階段常見的主要有小燈泡、電動機等儀器。像小燈泡這些非線性元件直接計算其電壓和電流比較困難，所以很難計算其實際功率。但是通過對描繪小燈泡的伏安特性曲線的學習，如果知道小燈泡的U-I圖線關系，把小燈泡接入已知電源，可以在同一個U-I圖線上描繪閉合電路歐姆定律的表達式和小燈泡的伏安特性圖線，兩條線的交點為小燈泡的電流I和電壓U，由P=UI即可計算出小燈泡的功率。但是當電路比較復雜時，直接寫出小燈泡的U、I關系可能會存在一定的難度，那么我們可以借助“等效電源”的方法把電路簡化。

【例3】如圖16，電路中R1=R2=18 Ω，電源電動勢E=12 V，內阻可以忽略不計，小燈泡的伏安特性曲線如圖17所示的I-U圖線，當開關S閉合后小燈泡的功率是多少？

圖16

圖17

圖18

其中U為小燈泡兩端的電壓，I為流過小燈泡的電流，代入數據得函數6=U+9I

作出等效電源的I-U圖像如圖19所示，則兩條線的交點可以得到小燈泡的電流I=0.50 A、電壓U=1.3 V，所以得到小燈泡的功率P=UI=0.65 W。

圖19

從此題可以看出，應用等效電源的方法計算非線性元件的功率可以使復雜的電路簡單化，通過等效電源的I-U圖線與小燈泡的I-U圖線的交點即可得到非線性元件的電流和電壓。這樣的方法不僅使問題簡單，還可以讓學生通過問題的探究，尋找處理復雜問題的方法，培養學生思維的靈活性和發散性。