一種改進的自適應閾值分塊曲面濾波方法

歐海軍， 馮騰飛， 沈月千， 張 堅

(1.廣州市城市規劃勘測設計研究院， 廣州 510053； 2.同濟大學測繪與地理信息學院， 上海 200092；3.河海大學地球科學與工程學院， 南京 211100)

機載激光雷達系統(light detection and ranging， LiDAR)是一種以飛機為載體的集激光測距、全球定位系統(GPS)和慣性導航系統(INS)三種技術優點于一體的系統，通過三種技術的結合，能夠精準地測定激光束落在激光腳點的三維空間坐標，從而獲得地物的三維坐標點云數據[1]。但與其他數據類型不同，由于LiDAR點云數據分布反映著地物表面的空間變化，具有數據量大且分布較為離散等特點，因此對點云進行后續處理前，必須率先進行三維點云數據濾波，以便實現更快速、高效的點云分類及地物提取[2]。

濾波算法性能的提升及其在不同地形的適用性一直備受中外學者的關注。Sithole等[3]提出了基于地形坡度的濾波算法，該算法通過對比目標點與其臨近點間的高差值與給定閾值之間的大小關系，判斷目標點是否為地面點，但該方法地形坡度閾值設置為30%，并不適用于起伏較大的區域；Kraus等[4]提出了迭代最小二乘線性內插的濾波算法，利用原始點云與最小二乘內插的擬合高程求差，并根據差值是否服從正態分布來判斷待定點是否為非地面點，但該算法只適用于地形起伏不大的機載點云區域，對于地形復雜的區域，擬合平面會隨著地面的起伏變化而變化，進而造成較差的濾波效果，且數據插值固有的誤差會增加濾波過程的不確定性；Lindenmayer等[5]提出了基于圖像處理方式的數學形態學濾波算法，該方法在濾波區域選擇一個固定大小的窗口，并利用窗口中其他點與預先運用數學形態運算找到的最低點求差，通過與設定閾值的比較進行判斷，若差值小于閾值則為地面點，該方法也采用了固定閾值的方式，增加了濾波困難；張小紅[6]和劉經南等[7]均基于激光腳點在一定程度上能夠反映地形表面的空間起伏變化這一原理提出了移動曲面擬合濾波算法，該方法利用曲面擬合的高程與實際點云數據的高差與固定的閾值比較，從而判別地面點，但該方法不僅需要尋找種子區域，還采用了固定閾值，對濾波效果造成較大影響。此外，李鵬程等[8]基于高于地面3 m的點為非地面點，采用區塊索引機制將整個點云區域分成很多區塊，提出基于距離圖像的分塊曲面濾波方法，該方法很大程度上依賴于區塊大小的確定，而區塊的確定需要人工干預，大大增加了工作量。

對比現有的LiDAR點云數據濾波方法可知大部分方法存在一定的共同點及局限性。首先，一些算法需要在濾波之前對數據進行插值處理，以此來減少存儲空間，提高運算速度，但在數據內插的過程中會破壞點云數據本身存在的內在性質以及點云之間的鄰近關系，最終使得濾波的效果并不佳[9-12]；其次，部分算法需要選擇含地面點的種子區域，但選取方法缺乏科學的驗證，可能會造成由于種子區域選取不當帶來的濾波精度損失；此外，絕大部分的濾波都需要設定濾波閾值，但固定且單一的閾值使算法很大程度上不能自適應地形的變化，造成較差的濾波效果。基于上述分析，提出一種改進的自適應閾值分塊濾波算法。一方面，對原始點云進行不斷的分塊，降低計算時內存的占用空間，加快算法的計算速度；另一方面，對分塊點云進行既定坡度平面擬合，對超出自適應濾波閾值的點進行分類，并不斷進行計算，最終達到地面點與非地面點分離的效果。

1 算法原理

1.1 點云去噪

點云數據在獲取的過程中會產生噪聲，這些噪聲會嚴重干擾點云濾波的過程，甚至可能造成點云數據濾波的失敗。因此點云濾波之前，必須對點云數據進行去噪處理。為了更好地得到無噪聲數據，采用“兩步走”的方式進行去噪，首先利用高斯濾波對點云進行處理:根據點云中所有點的距離應構成高斯分布這一特性，計算每個點與其最鄰近k個點的平均距離，并取其平均值與方差作為參考值，進而根據“3倍中誤差準則”[13]剔除異常點。此外，由于試驗數據為無序點云，高斯濾波去噪可能存在剔除空洞，因此利用K-D(K-dimensional)樹去噪的方式進行二次去噪:對已經進行粗去噪的點云數據構建K-D樹，并隨機取點求平均高差d，刪除所有大于2d的點，實現點云去噪，為點云濾波提供更精確的基礎點云數據。

1.2 傳統分塊曲面濾波算法

在傳統分塊曲面濾波算法中，通常將原始點云分塊后，對每一塊點云進行濾波，從而分離地面點與非地面點，其基本步驟及尚存問題分析[14-15]如下。

(1)建立區塊索引機制。分塊曲面濾波算法利用建立區塊索引的方式對離散的點云數據進行組織，使離散點云可以有效的進行索引定位和處理。

(2)利用距離圖像確定分塊數。根據一定的重采樣間距將離散點云數據組織為規則格網數據，每個格網中點云的高程均值為該網格的高程信息數據，并對所得數據進行歸化處理，生成距離圖像，結合圖像中最大建筑物的跨度來確定區塊的高度與寬度，從而確定分塊數，但是相對于海量的點云數據，該操作效率非常低。

(3)點云濾波。對上面所建立的所有區塊進行曲面擬合，選取塊內一定數量的高程點作為曲面擬合初點進行曲面擬合，并計算塊內其他點云高程與擬合高程的差值，使其與固定閾值作比較，如果小于或等于給定的閾值，則判定該點為地面點，否則為非地面點。這樣固定閾值的方式不僅不適用于所有的區塊，而且容易造成誤分現象。

1.3 改進的自適應閾值分塊曲面濾波算法

傳統的分塊曲面濾波算法利用區塊索引的方式進行組織，其分塊的方式取決于離散點云所生成的灰度圖像，與大部分濾波算法類似，一般根據經驗來選擇閾值，比較常用的是3 m或者5 m，但在實際中，固定的閾值往往使濾波結果出現不同程度的點云錯分現象(濾波算法誤差)，從而造成點云濾波的兩類錯誤增加，不利于點云的后續處理。同時人工選取圖像最大建筑物跨度也加大了工作量。因此，通過考慮分塊面積以及塊域內最大高程差兩個閾值影響因素建立自適應閾值模型，提出了一種改進的自適應閾值分塊曲面濾波算法，其詳細過程如下。

Step1建立虛擬網格。由于曲面擬合至少需要6個點位數據，而每次選取的點位均為塊內最低高程點位，因此將離散點云區域分割成6塊，且以包含點云的最小矩形窗口為初始窗口。

Step2自動選取種子點云。在分塊完成之后，獲取每塊3個最低的點位并取平均值，降低每塊去噪過程中造成的影響，利用所獲得的點位作為擬合曲面的初始種子點，避免人工選取種子區域。

Step3地面點的獲取。利用所選種子點位進行曲面擬合，分別計算每個點位高程與擬合曲面高程的差值，差值小于自適應閾值的點即為地面點，否則為非地面點。其中自適應閾值的確定如下。

在改進算法實現過程中，隨著分塊次數的增加，分塊面積也隨之不斷的縮小，因此濾波閾值應具有以下特點:

(1)面積越大，閾值越大，當面積增大的某種程度時，閾值不再隨面積增大而變化。

(2)閾值隨著面積的遞減而漸趨穩定，當面積減小到一定的值時，閾值不再變化。根據上述特點，建立閾值與塊域面積的函數關系，利用控制變量法，對多塊點云進行反復試驗，直到達到濾波效果的最優，并利用最小二乘方法，擬合建立所記錄閾值與對應塊域面積的函數關系。

(3)盡管上述函數在整體上表現最優，但當塊域起伏較大時，濾波的效果并不佳，因此除了面積這一因素之外，還需考慮與對應面積中的地形起伏，而最大高程差能夠體現出地形起伏的特點，且每塊點云數據中最大高程差也很大程度上反映了分塊點云的空間狀態。因此基于上述分析建立了顧及塊域面積以及塊域內最大高差兩個因素的自適應閾值模型，經過點云數據初步修正和實驗驗證，得到自適應閾值與兩因素的關系式為

y=0.076 1s2-0.355 1s+0.228 2Δhmax+

2.727 9

(1)

式(1)中:y為兩種因素影響下的閾值;s為分塊面積;Δhmax為區塊中高差最大值。

Step4重復Step 1—Step 3，迭代濾波直到沒有新的地面點產生。

由于點云塊域隨著算法的進行，分塊區域內點云數目不斷減小，且塊數也在不斷減小，當塊數小于6時，不滿足曲面擬合條件，迭代終止。算法的主要流程如圖1所示。

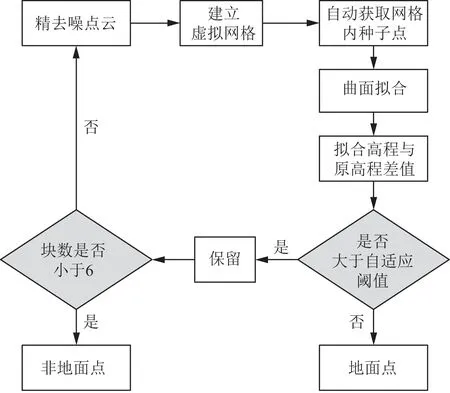
圖1 改進濾波算法流程圖

2 實驗結果與分析

采用具有不同特性的三組機載激光雷達點云影像作為實驗數據，如圖2所示，試驗區1包括植被、道路、建筑物(主要以廠房為主)以及建筑物附屬設施，整個區域包含195 990個點云數據，區域內最大高差約為20.27 m；試驗區2地勢較為平緩，包含復雜低矮的建筑物，建筑物較多，且植被較少，區域內最大高差約為30 m，包含162 426個離散點云；試驗區3包含較多植被、新蓋的樓盤以及較高古塔，區域內最大高差為40 m，包含174 417個離散點云。分別利用傳統分塊曲面濾波及自適應閾值分塊曲面濾波對三個試驗區點云影像進行處理，通過國際攝影測量與遙感協會(ISPRS)的評價體系驗證本文改進算法的可行性及優越性。該評價體系包括兩類誤差及總體誤差指標，其中第Ⅰ類誤差定義為將地面點誤分為非地面點的比例；第Ⅱ類誤差則是將非地面點誤分為地面點的比例；總體錯誤率即所有的類別錯分點占總點數比例，錯誤率越低代表整體濾波效果越好。具體如表1所示，第Ⅰ類誤差:b/e×100%；第Ⅱ類誤差:c/f×100%；總誤差:(b+c)/n×100%。

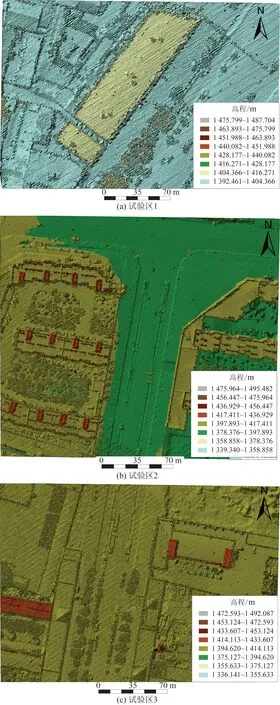
圖2 原始點云影像

表1 誤分率的定義

對上述實驗數據進行去噪，再分別利用傳統算法以及改進算法進行濾波，得到結果如圖3所示，其中圖3(a)和3(b)、圖3(e)和3(f)為傳統算法和本文改進算法對原始點云進行濾波得到的非地面點云對比圖，圖3(c)和圖3(d)為地面點云對比圖。就傳統方法濾波結果而言，分別存在地面點錯分為非地面點[圖3(c)紅圈所示]以及非地面點錯分為地面點[圖3(a)和圖3(e)紅圈所示]的現象。而對于改進算法的濾波結果，可以明顯看出，圖3(b)和圖3(d)中的第II類錯誤已基本消除，圖3(f)中第I類錯誤也明顯減小，三塊點云的錯分現象均得到了極大的改善，表明改進算法既能很好地適應不同地形，也解決了閾值選擇問題對濾波帶來的精度損失，濾波效果明顯優于傳統算法。

圖3 傳統算法與改進算法濾波效果對比

進一步利用誤差公式對傳統分塊濾波結果以及改進濾波結果進行定量評價，結果如表2和表3所示。由表2可知，I類誤差多于II類誤差，說明傳統算法更加側重于降低II類誤差。其中試驗區1和試驗區2的I類誤差都較II類誤差大，說明傳統算法在低矮建筑物較多的區域存在過濾現象，容易將地面點錯分為低矮建筑物。從表3可知，I類誤差明顯低于II類誤差，說明本文算法能很好地適應不同的地形，具有較強的魯棒性。此外，對比表2和表3中三類誤差，可以看出改進算法的濾波精度明顯提高。試驗區2的I類誤差幅度最大，說明改進算法更適用于建筑物較多、植被較少的地勢。與傳統分塊濾波算法相比，I類誤差值降低幅值較大，說明改進算法有更強的適應性。通過對II類誤差的對比分析，改進算法相比于傳統分塊濾波算法II類誤差最大降低了3.34%，最小降低0.15%。總誤差最大降低了4.73%，最小降低了0.41%，說明了改進算法比傳統分塊曲面濾波有更高的精度。

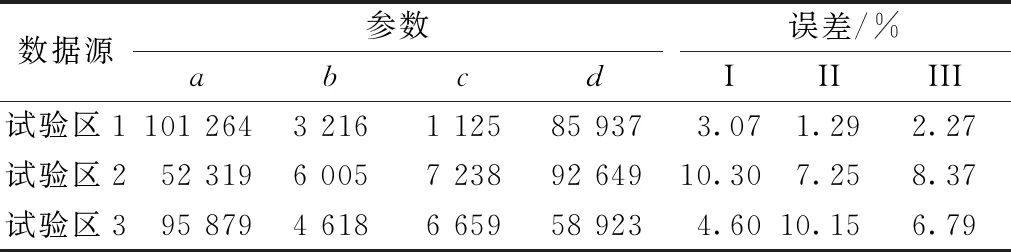
表2 傳統濾波算法誤差評價

表3 改進濾波算法誤差評價

綜上所述，無論是在低矮建筑區，還是在復雜多植被的城區，改進算法都能夠顯著減低I類誤差和II類誤差，驗證了改進算法的適用性以及有效性。

3 結論

利用網格法對點云進行逐級分塊，并以曲面擬合的方式自動獲取塊域種子點，同時顧及分塊面積及塊域內最大高程差兩個閾值影響因素建立了自適應閾值模型，從而提出一種改進的自適應閾值分塊曲面濾波算法，很好地滿足了機載LiDAR點云濾波的要求。實驗結果表明改進算法在濾波時能夠實現更有效的閾值選擇，且濾波精度較傳統方法有明顯提高。但對于閾值的影響因素還需進一步研究，以期實現更高精度的自適應閾值模型。